Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T17:37:21.444Z Has data issue: false hasContentIssue false
  • English
  • Français

The þ-function in λ-K-conversion

Published online by Cambridge University Press:  12 March 2014

A. M. Turing
A. M. Turing*
Affiliation:
Princeton University
Get access Rights & Permissions [Opens in a new window]

Extract

In the theory of conversion it is important to have a formally defined function which assigns to any positive integer n the least integer not less than n which has a given property. The definition of such a formula is somewhat involved: I propose to give the corresponding formula in λ-K-conversion, which will (naturally) be much simpler. I shall in fact find a formula þ such that if T be a formula for which T(n) is convertible to a formula representing a natural number, whenever n represents a natural number, then þ(T, r) is convertible to the formula q representing the least natural number q, not less than r, for which T(q) conv 0.2 The method depends on finding a formula Θ with the property that Θ conv λu·u(Θ(u)), and consequently if M→Θ(V) then M conv V(M). A formula with this property is,

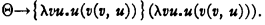
The formula þ will have the required property if þ(T, r) conv r when T(r) conv 0, and þ(T, r) conv þ(T, S(r)) otherwise. These conditions will be satisfied if þ(T, r) conv T(r, λx·þ(T, S(r)), r), i.e. if þ conv {λptr·t(r, λx·p(t, S(r)), r)}(þ). We therefore put,

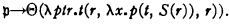
This enables us to define also a formula,

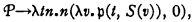
such that 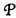(T, n) is convertible to the formula representing the nth positive integer q for which T(q) conv 0.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 2 , Issue 4 , December 1937 , pp. 164
Copyright
Copyright © Association for Symbolic Logic 1937

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Such a function was first defined by Kleene, S. C., A theory of positive integers in formal logic, American journal of mathematics, vol. 57 (1934), see p. 231 Google Scholar.

2 For the definition of λ-K-conversion see Kleene, S. C., λ-definability and recursiveness, Duke mathematical journal, vol. 2 (1936), pp. 340–353, footnote 12CrossRefGoogle Scholar. In λ-K-conversion we are able to define the formula 0 → λfx·x. The same paper of Kleene contains the definition of a formula L with a property similar to the essential property of Θ (p. 346).

3 “Convertible” and “conv” refer to λ-K-conversion throughout this note.