Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T18:53:09.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Martin's axioms, measurability and equiconsistency results

Published online by Cambridge University Press:  12 March 2014

Jaime I. Ihoda  and
Saharon Shelah
Jaime I. Ihoda*
Affiliation:
Institute of Mathematics, The Hebrew University, Jerusalem, Israel
Saharon Shelah
Affiliation:
Institute of Mathematics, The Hebrew University, Jerusalem, Israel
*
Department of Mathematics, University of California, Berkeley, California 94720
Get access Rights & Permissions [Opens in a new window]

Abstract

We deal with the consistency strength of ZFC + variants of MA + suitable sets of reals are measurable (and/or Baire, and/or Ramsey). We improve the theorem of Harrington and Shelah [2] repairing the asymmetry between measure and category, obtaining also the same result for Ramsey. We then prove parallel theorems with weaker versions of Martin's axiom (MA(σ-centered), (MA(σ-linked)), 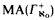, MA(K)), getting Mahlo, inaccessible and weakly compact cardinals respectively. We prove that if there exists r ∈ R such that 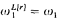and MA holds, then there exists a -selective filter on ω, and from the consistency of ZFC we build a model for ZFC + MA(I) + every -set of reals is Lebesgue measurable, has the property of Baire and is Ramsey.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 1 , March 1989 , pp. 78 - 94
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carlson, T., Unpublished notes.Google Scholar
[2]Harrington, L. and Shelah, S., Some exact equiconsistency results in set theory, Notre Dame Journal of Formal Logic, vol. 26 (1985), pp. 178–188.CrossRefGoogle Scholar
[3]Ihoda, J., Some consistency results on projective sets of reals, Israel Journal of Mathematics (submitted).Google Scholar
[4]Ihoda, J., -sets of reals, this Journal, vol. 53 (1988), pp. 636–642.Google Scholar
[5]Ihoda, J., Strong measure zero sets and rapid filters, this Journal, vol. 53 (1988), pp. 393–402.Google Scholar
[6]Ihoda, J. and Shelah, S., Souslin forcing, this Journal, vol. 53 (1988), pp. 1188–1207.Google Scholar
[7]Kunen, K. and Roitman, J. (in preparation).Google Scholar
[8]Martin, D. and Solovay, R., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), pp. 143–178.CrossRefGoogle Scholar
[9]Mathias, A., A remark on rare filters, Infinite and finite sets, Colloquia Mathematica Societatis János Bolyai, vol. 10, part 3, North-Holland, Amsterdam, 1975, pp. 1095–1097.Google Scholar
[10]Raisonnier, J., A mathematical proof of S. Shelah's theorem on the measure problem and related results, Israel Journal of Mathematics, vol. 48 (1984), pp. 48–56.CrossRefGoogle Scholar
[11]Shelah, S., Can you take Solovay's inaccessible away? Israel Journal of Mathematics, vol. 48 (1984), pp. 1–47.CrossRefGoogle Scholar
[12]Solovay, R., A model of set theory in which every set of reals is Lebesgue measurable, Annals of Mathematics, ser. 2, vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar
[13]Talagrand, M., Compacts de fonctions mesurables et filtres non mesurables, Studia Mathematica, vol. 67 (1980), pp. 13–43.CrossRefGoogle Scholar