Using side-by-side Sacks forcing, it is shown that it is consistent that 2ω be large and that there be many types of ultrafilters of character ω1.

The aim of this paper is to enrich the algebraic-axiomatic approach to recursion theory developed in [1] by an analogue to the classical arithmetical hierarchy and an abstract notion of degree. The results presented here are rather initial and elementary; indeed, the main problem was the very choice of right abstract concepts.

For several years much research has been directed at ideals associated with large cardinals. In this paper we discuss ideal families and use this tool to investigate the saturation properties of various large cardinal ideals.

Much of the work in this paper is a direct outgrowth of material presented in my doctoral dissertation written at the University of Michigan under the patient guidance of Andreas Blass. I would also like to thank the referee for several helpful questions and comments on the original version of this paper.

Working in the language of first-order arithmetic we consider models of the base theory P−. Suppose M is a model of P− and let M satisfy induction for Σ1-formulas. First it is shown that the Friedberg-Muchnik finite injury argument can be performed inside M, and then, using a blocking method for the requirements, we prove that the Sacks splitting construction can be done in M. So, the “amount” of induction needed to perform the known finite injury priority arguments is Σ1-induction.

We use models of set theory described in [2] and [3] to prove the consistency of several combinatorial principles, for example:

If ℱ is any filter on N containing all the cofinite sets, then there is a finite-to-one function f: N → N such that f(ℱ) is either the filter of cofinite sets or an ultrafilter.

As a consequence of our combinatorial principles, we also obtain the consistency of:

The partial ordering P of slenderness classes of abelian groups, denned and studied in [4], is a four-element chain.

In the remainder of this Introduction, we shall define our terminology and state the combinatorial principles to be considered. In §2, we shall establish some implications between these principles. In §3, we shall prove our consistency results by showing that the strongest of our principles holds in models of set theory constructed in [2] and [3].

A filter on N will always mean a proper filter containing all cofinite sets; in particular, an ultrafilter will necessarily be nonprincipal. We write N ↗ N for the set of nondecreasing functions from the set N of positive integers into itself. A subset ℐ of N ↗ N is called an ideal if it is closed downward (if f(n) ≤ g(n) for all n and if g ∈ ℐ, then f ∈ ℐ) and closed under binary maximum (if f(n) = max(g(n), h(n)) for all n and if g, h ∈ ℐ then f ∈ ℐ).

In this paper, we show that non-well-founded sets can be defined constructively by formalizing Hallnäs' limit definition of these within Martin-Löfs theory of types. A system is a type W together with an assignment of and to each ∝ ∈ W. We show that for any system W we can define an equivalence relation =w such that ∝ =w ß ∈ U and =w is the maximal bisimulation. Aczel's proof that CZF can be interpreted in the type V of iterative sets shows that if the system W satisfies an additional condition (*), then we can interpret CZF minus the set induction scheme in W. W is then extended to a complete system W* by taking limits of approximation chains. We show that in W* the antifoundation axiom AFA holds as well as the axioms of CFZ−.

Among the symbolic languages used most frequently in the indirect interpretation of natural language are Montague's Intensional Logic IL [5, 384ff.] and its extensional counterpart, the language Ty2 of two-sorted type theory. The question of which of these two formal languages is to be preferred has been obscured by lack of knowledge about the exact relation between them. The present paper is an attempt to clarify the situation by showing that, modulo a small, decidable class of formulas irrelevant to these applications, IL and Ty2 are equivalent in the strong sense that there exists a reversible translation between the terms of either language.

In [3, 6Iff.] Gallin has shown that there exists a simple and natural translation * of IL into Ty2. Following Gallin's translation procedure, it is even possible to conceive of IL as a highly restricted sublanguage of Ty2, viz. as that part which only contains expressions of certain intensional types plus one variable of the basic type of indices or worlds. In an obvious sense, this sublanguage has less expressive power than the whole of Ty2, where it is possible to express conditions on entities that do not even exist in IL's ontology. However, by a certain amount of coding, one can translate Ty2 into IL [3, 105]. Conditions on nonintensional entities then become conditions on corresponding intensional objects; and these paraphrases preserve (standard) validity and entailment. On the other hand, this retranslation of Ty2 into IL is not an inversion of *, as can be seen from a simple example.

We deal with the consistency strength of ZFC + variants of MA + suitable sets of reals are measurable (and/or Baire, and/or Ramsey). We improve the theorem of Harrington and Shelah [2] repairing the asymmetry between measure and category, obtaining also the same result for Ramsey. We then prove parallel theorems with weaker versions of Martin's axiom (MA(σ-centered), (MA(σ-linked)), , MA(K)), getting Mahlo, inaccessible and weakly compact cardinals respectively. We prove that if there exists r ∈ R such that and MA holds, then there exists a -selective filter on ω, and from the consistency of ZFC we build a model for ZFC + MA(I) + every -set of reals is Lebesgue measurable, has the property of Baire and is Ramsey.

Throughout this paper κ denotes an infinite cardinal, S = Sym(κ) and G is a subgroup of S. We shall be seeking the subgroups G with [S: G] < 2κ. In [2], the following result was proved.

Theorem 1. If [S: G] ≤ κthen there exists a subset Δ of k such that ∣Δ∣ < k and S(Δ) ≤ G.

Here S(Δ) = Sym(K/⊿) is the pointwise stabilizer of Δ in S.

However, the converse of Theorem 1 is not true. For if cf(κ) ≤ ∣Δ∣ < κ, then [S: S(Δ)] ≥ κcf(κ) > κ. This suggests that a substantially sharpened version of Theorem 1 may be true.

Question 1 [2]. Is it provable in ZFC, or even in ZFC with GCH, that if [S: G] ≤ κ then there is a subset Δ of κ such that ∣Δ∣ < cf(κ) and S(Δ) ≤ G?

At least two of the authors of [2] made a serious attempt to answer the above question positively. In §3, we shall see that they were essentially trying to prove that measurable cardinals do not exist.

The following result, due independently to Semmes [5] and Neumann [2], suggests a second way in which Theorem 1 might be improved.

Theorem 2. If k = ℵ0andthen there is a finite subset Δ of k such thatS(Δ) ≤ G.

Question 2 [2]. Is it provable in ZFC that if [S: G] < 2κ then there is a subset Δ of κ such that ∣Δ∣ < κ and S(Δ) < G?

This question will be answered negatively in §4.

The paper [Schütte + Simpson] deals with the following one-dimensional case of Friedman's extension (see in [Simpson 1]) of Kruskal's theorem ([Kruskal]). Given a natural number n, let Sn+1 be the set of all finite sequences of natural numbers <n + 1. If s1 = (a0,…,ak) ∈Sn+1 and s2 = (b0,…,bm) ∈Sn + 1, then a strictly monotone function f: {0,…, k} → {0,…, m} is called an embedding of s1 into s2 if the following two assertions are satisfied:

1) ai, = bf(i), for all i < k;

2) if f(i) < j < f(i + 1) then bj > bf(i+1), for all i < k, j < m.

Then for every infinite sequence s1, s2,…,sk,… of elements of Sn + 1 there exist indices i < j and an embedding of si into Sj. That is, Sn+1 forms a well-quasi-ordering (wqo) with respect to embeddability. For each n, this statement W(Sn+1) is provable in the standard second order conservative extension of Peano arithmetic. On the other hand, the proof-theoretic strength of the statements W(Sn+1) grows so fast that this formal theory cannot prove the limit statement ∀nW(Sn+1). The appropriate first order 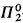-versions of these combinatory statements preserve their proof-theoretic strength, so that actually one can speak in terms of provability in Peano arithmetic. These are the main conclusions from [Schütte + Simpson].

We wish to extend this into the transfinite. That is, we take an arbitrary countable ordinal τ > 0 instead of n + 1 and try to obtain an analogous “strong” combinatory statement about finite sequences of ordinals < τ.

Let L(Q) be first order logic with Keisler's quantifier, in the λ+ interpretation (= the satisfaction is defined as follows: M ⊨ (Qx)φ(x) means there are λ+ many elements in M satisfying the formula φ(x)).

Theorem 1. Let λ be a singular cardinal; assume □λ and GCH. If T is a complete theory in L(Q) of cardinality at most λ, and p is an L(Q) 1-type so that T strongly omits p( = p has no support, to be defined in §1), then T has a model of cardinality λ+ in the λ+ interpretation which omits p.

Theorem 2. Let λ be a singular cardinal, and let T be a complete first order theory of cardinality λ at most. Assume □λ and GCH. If Γ is a smallness notion then T has a model of cardinality λ+ such that a formula φ(x) is realized by λ+ elements of M iff φ(x) is not Γ-small. The theorem is proved also when λ is regular assuming λ = λ<λ. It is new when λ is singular or when ∣T∣ = λ is regular.

Theorem 3. Let λ be singular. If Con(ZFC + GCH + ∃κ) [κ is a strongly compact cardinal]), then the following is consistent: ZFC + GCH + the conclusions of all above theorems are false.

Let S and T be countable complete theories. We assume that T is superstable without the dimensional order property, and S is interpretable in T in such a way that every model of S is coded in a model of T. We show that S does not have the dimensional order property, and we discuss the question of whether Depth(S) ≤ Depth(T). For Mekler's uniform interpretation of arbitrary theories S of finite similarity type into suitable theories TS of groups we show that Depth(S) ≤ Depth(TS) ≤ 1 + Depth(S).

Posner [6] has shown, by a nonuniform proof, that every degree has a complement below 0′. We show that a 1-generic complement for each set of degree between 0 and 0′ can be found uniformly. Moreover, the methods just as easily can be used to produce a complement whose jump has the degree of any real recursively enumerable in and above ∅′. In the second half of the paper, we show that the complementation of the degrees below 0′ does not extend to all recursively enumerable degrees. Namely, there is a pair of recursively enumerable degrees a above b such that no degree strictly below a joins b above a. (This result is independently due to S. B. Cooper.) We end with some open problems.

In [KP] we have studied the problem of determining when a subset of a (countable) model M of PA can be coded in an elementary end extension of M. Sets with this property are called elementary extensional. In particular we can ask whether there are elementary extensional subsets of a model which have order type ω. It turns out that having elementary extensional subsets of order type ω is an interesting property connected with other structural properties of models of PA. We will call this property the ω-property. In [KP] the problem of characterizing models with the ω-property was left open. It is still open, and the aim of this paper is to present a collection of results pertaining to it. It should be mentioned that the same notion was studied by Kaufmann and Schmerl in [KS2] in connection with some weak notions of saturation which they discuss there. Our notion of a model with the ω-property corresponds to the notion of an upward monotonically ω-lofty cut.

It is fairly easy to see that countable recursively saturated models (or in fact all recursively saturated models with cofinality ω) and all short recursively saturated models have the ω-property (Proposition 1.2 below). On the other hand, if we had asked the question about the existence of models with the ω-property before 1975 (when recursively saturated models were introduced) the answer would probably not have been that easy and we would have to come to notions close to recursive saturation.

We introduce a notion of complexity for interpretations, which is used to prove some new results about interpretations of sequential theories. In particular, we give a new, elementary proof of Pudlák's theorem that sequential theories are connected. We also demonstrate a counterexample to the infinitary distributive law

in the lattice of chapters, in which the chapters a and bi are compact. (Counterexamples in which a is not compact have been found previously.)

Kueker's conjecture is proved for stable theories, for theories that interpret a linear ordering, and for theories with Skolem functions. The proof of the stable case involves certain results on coordinatization that are of independent interest.

A stable theory is finitely based if every set of indiscernibles is based on a finite subset. This is a common generalization of superstability and 1-basedness. We show that if such theories have more than one model they must have infinitely many, and prove some other conjectures.

If ℱ is a normal filter on a regular uncountable cardinal κ, let ║f║ be the ℱ-norm of an ordinal function f. We introduce the class of positive ordinal operations and prove that if F is a positive operation then ║F(f)║ ≥ F(║f║). For each η < κ+ let fη be the canonical ηth function. We show that if F is a ∑ operation then F(fη) = fF(η).

As an application we show that if κ is greatly Mahlo then there are normal filters on κ of order greater than κ+.

A previously unexplored method, combining logical and mathematical elements, is shown to yield substantial numerical improvements in the area of Diophantine approximations. Kreisel illustrated the method abstractly by noting that effective bounds on the number of elements are ensured if Herbrand terms from ineffective proofs of Σ2-finiteness theorems satisfy certain simple growth conditions. Here several efficient growth conditions for the same purpose are presented that are actually satisfied in practice, in particular, by the proofs of Roth's theorem due to Roth himself and to Esnault and Viehweg. The analysis of the former yields an exponential bound of order exp(70ε−2d2) in place of exp(285ε−2d2) given by Davenport and Roth in 1955, where α is (real) algebraic of degree d ≥ 2 and ∣α − pq−1∣ < q−2−ε. (Thus the new bound is less than the fourth root of the old one.) The new bounds extracted from the other proof are polynomial of low degree (in ε−1 and log d). Corollaries: Apart from a new bound for the number of solutions of the corresponding Diophantine equations and inequalities (among them Thue's inequality), log log qν, < Cα, εν5/6+ε, where qν are the denominators of the convergents to the continued fraction of α.

An Ehrenfeucht theory is a complete first order theory with exactly n countable models up to isomorphism, 1 < n < ω. Numerous results have emerged regarding these theories ([1]–[15]). A general question in model theory is whether or not the number of countable models of a complete theory can be different than the number of countable models of a complete consistent extension of the theory by finitely many constant symbols. Examples are known of Ehrenfeucht theories that have complete extensions by finitely many constant symbols such that the extensions fail to be Ehrenfeucht ([4], [8], [13]). These examples are easily modified to allow finite increases in the number of countable models.

This paper contains examples in the other direction—complete theories that have consistent extensions by finitely many constant symbols such that the extensions have fewer countable models. This answers affirmatively a question raised by, among others, Peretyat'kin [8]. The first example will be an Ehrenfeucht theory with exactly four countable models with an extension by a constant symbol that has only three countable models. The second example will be a complete theory that is not Ehrenfeucht, but which has an extension by a constant symbol that is Ehrenfeucht. The notational conventions for this paper are standard.

Peretyat'kin introduced the theory of a dense binary branching tree with a meet operator [7]. Dense ω-branching trees have also proven useful [5], [11]. Both of the Theories that will be constructed make use of dense ω-branching trees.