Article contents
More on an undecidability result of Bateman, Jockusch and Woods
Published online by Cambridge University Press: 12 March 2014
Extract
Let P be the set of prime numbers. Theorem 1 of [1] shows that the linear case of Schinzel's Hypothesis (H) implies that multiplication is definable in 〈ω,+,P〉 and therefore that the first-order theory of this structure is undecidable. Let m be any fixed natural number >2, let R be the set of natural numbers <m which are prime to m, and let r be any fixed element of R. The set
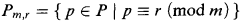
is infinite (Dirichlet). Theorem 1 of [1] can be improved as follows:
Proposition. The linear case of Schinzel's Hypothesis (H) implies that multiplication is definable in 〈ω,+,Pm,r〉 and therefore that the first-order theory of this structure is undecidable.
Proof. We follow [1] with the following new ingredients. Let k be the number of elements of R, i.e. k = ϕ(m) where ϕ is Euler's totient function. Since k is even, the polynomial g(n) = nk + n satisfies g(0) = g(−1) = 0, so (by Lemma 1 of [1]) it follows from the linear case of (H) that there are natural numbers al (l ϵ ω) such that al+g(0), al+g(1),…, al+g(l) are consecutive primes. Since R is finite, we may assume that all the al's have the same residue t in R, so that al+g(i) ≡ t+1+i (mod m) for i ϵ R. This implies that the function t+1+i (reduced mod m) gives a permutation of R, so we can find s ϵ R such that al+g(s) ≡ r (mod m). Consider the polynomial h(n) = g(s + mn) and let bl = as+ml. Then bl + h(0), bl + h(1),…, bl + h(l) are elements of Pm,r. They are not necessarily consecutive elements of Pm,r, but they are separated by a fixed number of elements of Pm,r. This implies that {h(n) ∣ n ϵ ω} is definable in 〈ω,+,Pm,r〉(by adapting the proof of Theorem 1 of [1]), and the result follows.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
- 1
- Cited by

