A set X of nonnegative integers is computably enumerable (c.e.), also called recursively enumerable (r.e.), if there is a computable method to list its elements. Let ε denote the structure of the computably enumerable sets under inclusion, ε = ({We}eϵω,⊆). We previously exhibited a first order ε-definable property Q(X) such that Q(X) guarantees that X is not Turing complete (i.e., does not code complete information about c.e. sets).

Here we show first that Q(X) implies that X has a certain “slowness” property whereby the elements must enter X slowly (under a certain precise complexity measure of speed of computation) even though X may have high information content. Second we prove that every X with this slowness property is computable in some member of any nontrivial orbit, namely for any noncomputable A ϵ ε there exists B in the orbit of A such that X ≤TB under relative Turing computability (≤T). We produce B using the -automorphism method we introduced earlier.

For x, y ϵ ℝω define the inner product

which may not be finite or even exist. We say that x and y are orthogonal if (x, y) converges and equals 0.

Define lp to be the set of all x ϵ ℝω such that

For Hilbert space, l2, any family of pairwise orthogonal sequences must be countable. For a good introduction to Hilbert space, see Retherford [4].

Theorem 1. There exists a pairwise orthogonal family F of size continuum such that F is a subset of lp for every p > 2.

It was already known that there exists a family of continuum many pairwise orthogonal elements of ℝω. A family F ⊆ ℝω∖0 of pairwise orthogonal sequences is orthogonally complete or a maximal orthogonal family iff the only element of ℝω orthogonal to every element of F is 0, the constant 0 sequence.

It is somewhat surprising that Kunen's perfect set of orthogonal elements is maximal (a fact first asserted by Abian). MAD families, nonprincipal ultrafilters, and many other such maximal objects cannot be even Borel.

Theorem 2. There exists a perfect maximal orthogonal family of elements of ℝω.

Abian raised the question of what are the possible cardinalities of maximal orthogonal families.

Theorem 3. In the Cohen real model there is a maximal orthogonal set in ℝω of cardinality ω1, but there is no maximal orthogonal set of cardinality κ with ω1 < κ < ϲ.

By the Cohen real model we mean any model obtained by forcing with finite partial functions from γ to 2, where the ground model satisfies GCH and γω = γ.

Let P be the set of prime numbers. Theorem 1 of [1] shows that the linear case of Schinzel's Hypothesis (H) implies that multiplication is definable in 〈ω,+,P〉 and therefore that the first-order theory of this structure is undecidable. Let m be any fixed natural number >2, let R be the set of natural numbers <m which are prime to m, and let r be any fixed element of R. The set

is infinite (Dirichlet). Theorem 1 of [1] can be improved as follows:

Proposition. The linear case of Schinzel's Hypothesis (H) implies that multiplication is definable in 〈ω,+,Pm,r〉 and therefore that the first-order theory of this structure is undecidable.

Proof. We follow [1] with the following new ingredients. Let k be the number of elements of R, i.e. k = ϕ(m) where ϕ is Euler's totient function. Since k is even, the polynomial g(n) = nk + n satisfies g(0) = g(−1) = 0, so (by Lemma 1 of [1]) it follows from the linear case of (H) that there are natural numbers al (l ϵ ω) such that al+g(0), al+g(1),…, al+g(l) are consecutive primes. Since R is finite, we may assume that all the al's have the same residue t in R, so that al+g(i) ≡ t+1+i (mod m) for i ϵ R. This implies that the function t+1+i (reduced mod m) gives a permutation of R, so we can find s ϵ R such that al+g(s) ≡ r (mod m). Consider the polynomial h(n) = g(s + mn) and let bl = as+ml. Then bl + h(0), bl + h(1),…, bl + h(l) are elements of Pm,r. They are not necessarily consecutive elements of Pm,r, but they are separated by a fixed number of elements of Pm,r. This implies that {h(n) ∣ n ϵ ω} is definable in 〈ω,+,Pm,r〉(by adapting the proof of Theorem 1 of [1]), and the result follows.

Small forcing always ruins the indestructibility of an indestructible supercompact cardinal. In fact, after small forcing, any cardinal κ becomes superdestructible—any further <κ-closed forcing which adds a subset to κ will destroy the measurability, even the weak compactness, of κ. Nevertheless, after small forcing indestructible cardinals remain resurrectible, but never strongly resurrectible.

It has been known for more than thirty years that the degree of a non-standard model of true arithmetic is a subuniform upper bound for the arithmetic sets (suub). Here a notion of generic enumeration is presented with the property that the degree of such an enumeration is an suub but not the degree of a non-standard model of true arithmetic. This answers a question posed in the literature.

It was conjectured by Halpern and Kapron (Annals of Pure and Applied Logic, vol. 69, 1994) that frame satisfiability of propositional modal formulas is incomparable in expressive power to both (Ackermann) and (Bernays-Schönfinkel). We prove this conjecture. Our results imply that (Ackermann) and (Bernays-Schönfinkel) are incomparable in expressive power, already on finite graphs. Moreover, we show that on ordered finite graphs, i.e., finite graphs with a successor, (Bernays-Schönfinkel) is strictly more expressive than (Ackermann).

Let K be an algebraically closed field of any characteristic, complete with respect to the non-trivial ultrametric absolute value ∣·∣: K → ℝ+. By R denote the valuation ring of K, and by ℘ its maximal ideal. We work within the class of subanalytic sets defined in [5], but our results here also hold for the strongly subanalytic sets introduced in [11] as well as for those subanalytic sets considered in [6]. Let X ⊂ R1 be subanalytic. In [8], we showed that there is a decomposition of X as a union of a finite number of special sets U ⊂ R1 (see below). In this note, in Theorem 1.6, we obtain a version of this result which is uniform in parameters, thereby answering a question brought to our attention by Angus Macintyre. It follows immediately from Theorem 1.6 that the theory of K in the language 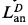(see [5] and [6]) is C-minimal in the sense of [3] and [9]. The analogous uniformity result in the p-adic case was recently proved in [12].

Definition 1.1. (i) A disc in R1 is a set of one of the two following forms:

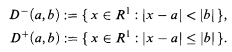
A special set in R1 is a disc minus a finite union of discs.

(ii) R-domains u ⊂ Rm, and their associated rings of analytic functions, 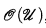, are defined inductively as follows. Rm is an R-domain and 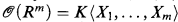, the ring of strictly convergent power series in X1,…, Xm over K. If u is an R-domain with associated ring 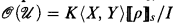, (where K 〈X, Y〉 〚ρ〛S is a ring of separated power series, see [5, §2] and [1, §1]) and f, 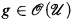have no common zero on u and ◸ ϵ {<, ≤}, then

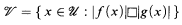
is an R-domain and

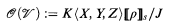
where J is the ideal generated by I and f − gZ (Z is a new variable) if ◸ is ≤, and

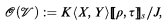
where J is the ideal generated by I and f − gτ (τ a new variable) if ◸ is <. (See [8, Definition 2.2].) R-domains generalize the rational domains of [2, §7.2.3]. It is true, but not easy to prove, that 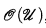only depends on u as a point set, and is independent of the particular representation of u.

Let λ ≤ κ be infinite cardinals and let Ω be a set of cardinality κ. The bounded permutation group Bλ(Ω), or simply Bλ, is the group consisting of all permutations of Ω which move fewer than λ points in Ω. We say that a permutation group G acting on Ω is a supplement of Bλ if BλG is the full symmetric group on Ω.

In [7], Macpherson and Neumann claimed to have classified all supplements of bounded permutation groups. Specifically, they claimed to have proved that a group G acting on the set Ω is a supplement of Bλ if and only if there exists Δ ⊂ Ω with ∣Δ∣ < λ such that the setwise stabiliser G{Δ} acts as the full symmetric group on Ω ∖ Δ. However I have found a mistake in their proof. The aim of this paper is to examine conditions under which Macpherson and Neumann's claim holds, as well as conditions under which a counterexample can be constructed. In the process we will discover surprising links with cardinal arithmetic and Shelah's recently developed pcf theory.

The monadic second-order theory of trees allows quantification over elements and over arbitrary subsets. We classify the class of trees with respect to the question: does a tree T have definable Skolem functions (by a monadic formula with parameters)? This continues [6] where the question was asked only with respect to choice functions. A natural subclass is defined and proved to be the class of trees with definable Skolem functions. Along the way we investigate the spectrum of definable well orderings of well ordered chains.

Let I be an ideal of subsets of a Polish space X, containing all singletons and possessing a Borel basis. Assuming that I does not satisfy ccc, we consider the following conditions (B), (M) and (D). Condition (B) states that there is a disjoint family F ⊆ P(X) of size ϲ, consisting of Borel sets which are not in I. Condition (M) states that there is a Borel function f : X → X with f−1[{x}] ∉ I for each x ∈ X. Provided that X is a group and I is invariant, condition (D) states that there exist a Borel set B ∉ I and a perfect set P ⊆ X for which the family {B+x : x ∈ P} is disjoint. The aim of the paper is to study whether the reverse implications in the chain (D) ⇒ (M) ⇒ (B) ⇒ not-ccc can hold. We build a σ-ideal on the Cantor group witnessing (M) & ¬(D) (Section 2). A modified version of that σ-ideal contains the whole space (Section 3). Some consistency results on deriving (M) from (B) for “nicely” defined ideals are established (Sections 4 and 5). We show that both ccc and (M) can fail (Theorems 1.3 and 5.6). Finally, some sharp version's of (M) for invariant ideals on Polish groups are investigated (Section 6).

Using an idea developed in joint work with Shelah, we show how to redefine Laver's notion of forcing making a supercompact cardinal κ indestructible under κ-directed closed forcing to give a new proof of the Kimchi-Magidor Theorem in which every compact cardinal in the universe (supercompact or strongly compact) satisfies certain indestructibility properties. Specifically, we show that if K is the class of supercompact cardinals in the ground model, then it is possible to force and construct a generic extension in which the only strongly compact cardinals are the elements of K or their measurable limit points, every κ ∈ K is a supercompact cardinal indestructible under ∈-directed closed forcing, and every κ a measurable limit point of K is a strongly compact cardinal indestructible under κ-directed closed forcing not changing ℘(κ). We then derive as a corollary a model for the existence of a strongly compact cardinal κ which is not κ+ supercompact but which is indestructible under κ-directed closed forcing not changing ℘(κ) and remains non-κ+ supercompact after such a forcing has been done.

Assuming that ORD is ω + ω-Erdös we show that if a class forcing amenable to L (an L-forcing) has a generic then it has one definable in a set-generic extension of L[O#]. In fact we may choose such a generic to be periodic in the sense that it preserve the indiscernibility of a final segment of a periodic subclass of the Silver indiscernibles, and therefore to be almost codable in the sense that it is definable from a real which is generic for an L-forcing (and which belongs to a set-generic extension of L[0#]). This result is best possible in the sense that for any countable ordinal α there is an L-forcing which has generics but none periodic of period ≤ α. However, we do not know if an assumption beyond ZFC+“O# exists” is actually necessary for these results.

Let P denote a class forcing definable over an amenable ground model 〈L, A〉 and assume that O# exists.

Definition. P is relevant if P has a generic definable in L[0#]. P is almost relevant if P has a generic definable in a set-generic extension of L[0#].

Remark. The reverse Easton product of Cohen forcings 2<κ, κ regular is relevant. So are the Easton product and the full product, provided κ is restricted to the successor cardinals. See Chapter 3, Section Two of Friedman [3]. Of course any set-forcing (in L) is almost relevant.

Definition. κ is α-Erdös if whenever C is CUB in κ and f: [C]<ω → κ is regressive (i.e., f(a) < min(a)) then f has a homogeneous set of ordertype α.

This paper explores algebraic aspects of two modifications of the usual account of first-order quantifiers.

Standard first-order quantificational logic is modelled algebraically by cylindric algebras. Prime examples of these are algebras whose members are sets of sequences: given a first-order model U for a language that is based on the set {υκ: κ < α} of variables, each formula φ is represented by the set

of all those α-length sequences x = 〈xκ: κ < α〉 that satisfy φ in U. Such a sequence provides a value-assignment to the variables (υκ is assigned value xκ), but it may also be viewed geometrically as a point in the α-dimensional Cartesian spaceαU of all α-length sequences whose terms come from the underlying set U of U. Then existential quantification is represented by the operation of cylindrification. To explain this, define a binary relation Tκ on sequences by putting xTκy if and only if x and y differ at most at their κth coordinate, i.e.,

Then for any set X ⊆ αU, the set

is the “cylinder” generated by translation of X parallel to the κth coordinate axis in αU. Given the standard semantics for the existential quantifier ∃υκ as

it is evident that

Starting with D. Scott's work on the mathematical foundations of programming language semantics, interest in topology has grown up in theoretical computer science, under the slogan ‘open sets are semidecidable properties’. But whereas on effectively given Scott domains all such properties are also open, this is no longer true in general. In this paper a characterization of effectively given topological spaces is presented that says which semidecidable sets are open.

This result has important consequences. Not only follows the classical Rice-Shapiro Theorem and its generalization to effectively given Scott domains, but also a recursion theoretic characterization of the canonical topology of effectively given metric spaces. Moreover, it implies some well known theorems on the effective continuity of effective operators such as P. Young and the author's general result which in its turn entails the theorems by Myhill-Shepherdson, Kreisel-Lacombe-Shoenfield and Ceĭtin-Moschovakis, and a result by Eršov and Berger which says that the hereditarily effective operations coincide with the hereditarily effective total continuous functionals on the natural numbers.

A definition of nonstandard universe which gets over the limitation to the finite levels of the cumulative hierarchy is proposed. Though necessarily nonwellfounded, nonstandard universes are arranged in strata in the likeness of superstructures and allow a rank function taking linearly ordered values. Nonstandard universes are also constructed which model the whole ZFC theory without regularity and satisfy the κ-saturation property.

We prove the undecidability of a very large class of restricted and unrestricted wreath products (Theorem 1.2), and of some skew fields of power series (Section2). Both undecidabilities are obtained by interpreting some enrichments of twisted wreath products, which are themselves proved to be undecidable (Proposition 1.1).

We consider division rings of power series in various languages:

We show (Theorem 2.8) that every power series division ring k((B)), whose field of constants k is commutative and whose ordered group of exponents is noncommutative with a convex center, is undecidable in every extension of the language of rings where the valuation and the ordered group B are definable.

For certain k and B we prove here the undecidability of the structure

where X↾k((B))xB is the restriction of the multiplication to k((B)) Χ B,and γ is a given conjugation of k((B)). This shows that we cannot hope to improve our previous result, a sort of Ax-Kochen-Ershov principle for power series division rings, which ensures that

is decidable for every decidable solvable B.

Quine's “New Foundations” (NF) was first presented in Quine [10] and later on in Quine [11]. Ernst Specker [15, 13], building upon a previous result of Ehrenfeucht and Mostowski [5], showed that NF is consistent if and only if there is a model of the Theory of Negative (and positive) Types (TNT) with full extensionality that admits of a “shifting automorphism,” but the existence of such a model remains an open problem.

In his [8], Ronald Jensen gave a partial solution to the problem of the consistency of Quine's NF. Jensen considered a version of NF—referred to as NFU—in which the axiom of extensionality is weakened to allow for Urelemente or “atoms.” He showed, modifying Specker's theorem, that the existence of a model of TNT with atoms admitting of a “shifting automorphism” implies the consistency of NFU, proceeding then to exhibit such a model.

This paper presents a reduction of the consistency problem for NF to the existence of a model of TNT with atoms containing certain “large” (unstratified) sets and admitting a shifting automorphism. In particular we show that such a model can be “collapsed” to a model of pure TNT in such a way as to preserve the shifting automorphism. By the above-mentioned result of Specker's, this implies the consistency of NF.

Let us take the time to explain the main ideas behind the construction. Suppose we have a certain universe U of sets, built up from certain individuals or “atoms.” In such a universe we have only a weak version of the axiom of extensionality: two objects are the same if and only if they are both sets having the same members. We would like to obtain a universe U′ that is as close to U as possible, but in which there are no atoms (i.e., the only memberless object is the empty set). One way of doing this is to assign to each atom ξ, a set a (perhaps the empty set), inductively identifying sets that have members that we are already committed to considering “the same.” In doing this we obtain an equivalence relation ≃ over U that interacts nicely with the membership relation (provided we have accounted for multiplicity of members, i.e., we have allowed sets to contain “multiple copies” of the same object). Then we can take U′ = U/≃, the quotient of U with respect to ≃. It is then possible to define a “membership” relation over U′ in such a way as to have full extensionality. Relations such as ≃ are referred to as “contractions” by Hinnion and “bisimulations” by Aczel.

Henson and Ross [1] answered the question of when two hyperfinite sets A, B in an ℵ1-saturated nonstandard universe are bijective by a Borel function: precisely when ∣A∣/∣B∣ ≈ 1. Živaljević [5] generalized this result to nonvanishing Borel sets. He defined a set to be nonvanishing if it is Loeb-measurable and has finite, non-zero measure with respect to some Loeb counting measure. He then showed that two nonvanishing Borel sets are Borel bijective just in case they have the same finite, non-zero measure with respect to some Loeb counting measure.

Here we shall complete the cycle, for Borel sets at least. For N ∈ *N, let λN be the internal counting measure given by λN(A) = ∣A∣/N for A internal. Then for vanishing Loeb-measurable sets B, it is natural to consider the Dedekind cut (BL, BR) on *N consisting of those N for which B has 0λN-measure infinity and zero, respectively. We show that, for all vanishing Borel sets B, B and BL are Borel bijective. It follows that vanishing Borel sets B and C are Borel bijective if, and only if, BL = CL. Combined with Živaljević's result, we can characterize when arbitrary Borel sets are Borel bijective: precisely when they have the same measure with respect to all Loeb counting measures.

In the final section, we generalize in a similar way results of [2] and [5] to characterize when two Borel sets are bijective by a countably determined function: precisely when, for all N, one has 0λN-measure 0 if and only if the other also has 0λN-measure 0.

We study the monadic fragment of second order intuitionistic propositional logic in the language containing the standard propositional connectives and propositional quantifiers. It is proved that under the topological interpretation over any dense-in-itself metric space, the considered fragment collapses to Heyting calculus. Moreover, we prove that the topological interpretation over any dense-in-itself metric space of fragment in question coincides with the so-called Pitts' interpretation. We also prove that all the nonstandard propositional operators of the form q ↦ ∃p (q ↔ F(p)), where F is an arbitrary monadic formula of the variable p, are definable in the language of Heyting calculus under the topological interpretation of intuitionistic logic over sufficiently regular spaces.

We prove the following theorems:

(1) If X has strong measure zero and if Y has strong first category, then their algebraic sum has property S0.

(2) If X has Hurewicz's covering property, then it has strong measure zero if, and only if, its algebraic sum with any first category set is a first category set.

(3) If X has strong measure zero and Hurewicz's covering property then its algebraic sum with any set in is a set in . ( is included in the class of sets always of first category, and includes the class of strong first category sets.)

These results extend: Fremlin and Miller's theorem that strong measure zero sets having Hurewicz's property have Rothberger's property, Galvin and Miller's theorem that the algebraic sum of a set with the γ-property and of a first category set is a first category set, and Bartoszyfński and Judah's characterization of -sets. They also characterize the property (*) introduced by Gerlits and Nagy in terms of older concepts.