Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T07:23:57.595Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Σ2-theory of the upper semilattice of Turing degrees

Published online by Cambridge University Press:  12 March 2014

Carl G. Jockusch Jr  and
Theodore A. Slaman
Carl G. Jockusch Jr
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801, E-mail: jockusch@symcom.math.uiuc.edu
Theodore A. Slaman
Affiliation:
Department of Mathematics, The University of Chicago, Chicago, Illinois 60637, E-mail: ted@zaphod.uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Extract

A first-order sentence Φ is Σ2 if there is a quantifier-free formula Θ such that Φ has the form 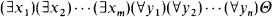. The Σ2-theory of a structure 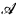for a language ℒis the set of Σ2-sentences of ℒ true in 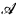. It was shown independently by Lerman and Shore (see [Le, Theorem VII.4.4]) that the Σ2-theory of the structure 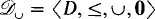= 〈D, ≤ 〉 is decidable, where D is the set of degrees of unsolvability and ≤ is the standard ordering of D. This result is optimal in the sense that the Σ3-theory of 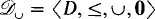is undecidable, a result due to J. Schmerl. (For a proof, see [Le, Theorem VII.4.5]. As Lerman has pointed out, this proof should be corrected by defining θσ to be ∀xσ1(x) rather than ∀x(ψ(x)→ σ1(x)).) Nonetheless, in this paper we extend the decidability result of Lerman and Shore by showing that the Σ2-theory of 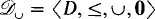is decidable, where ⋃ is the least upper bound operator and 0 is the least degree. Of course ⋃ is definable in 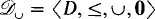, but many interesting degree-theoretic results are expressible as Σ2-sentences in the language of 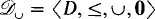∪ but not as Σ2-sentences in the language of 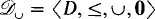. For instance, Simpson observed that the Posner-Robinson cupping theorem could be used to show that for any nonzero degrees a, b, there is a degree g such that b ≤ a ⋃ g, and b ⋠ g (see [PR, Corollary 6]). However, the Posner-Robinson technique does not seem to suffice to decide the Σ2-theory of 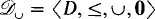∪. We introduce instead a new method for coding a set into the join of two other sets and use it to decide this theory.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 1 , March 1993 , pp. 193 - 204
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[La]Lachlan, A. H., The elementary theory of recursively enumerable sets, Duke Mathematical Journal, vol. 35 (1968), pp. 123–146.CrossRefGoogle Scholar
[Le]Lerman, M., Degrees of unsolvability, Perspectives in Mathematical Logic, Omega Series, Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1983.Google Scholar
[LS]Lerman, M. and Soare, R. I., A decidable fragment of the elementary theory of the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 257(1980), pp. 1–37.Google Scholar
[PR]Posner, D. and Robinson, R., Degrees joining to 0′, this Journal, vol. 46 (1981), pp. 705–713.Google Scholar