One of this author's favorite theorems has long been the Zero-One law discovered independently by Glebskii et al. [12] and Ron Fagin [10]. Let A be any first-order property of graphs and let µn(A) be the proportion of labelled graphs on n vertices for which A holds. Then

This result has inspired much work by logicians, generally in the direction of showing (1) for some powerful languages. Thus it is known [5] that (1) holds when A is a sentence in fixed point logic and it is known [13] that (1) does not always hold when A is a sentence in second-order monadic logic. Here, however, we explore recent work in a totally different direction. Let G(n, p) denote the random graph on n vertices with edge probability p. (In §2 we define the random structures we will deal with.) A property A is an event in the probability space and Pr[G(n, p) ╞ A] is well defined. When p = 1/2, each labelled graph on n vertices has equal weight so that (1) may be rewritten

Fagin's proof actually gives that (2) holds for any constant 0 < p < 1.

Does V = L? Is the Axiom of Constructibility true? Most people with an opinion would answer no. But on what grounds? Despite the near unanimity with which V = L is declared false, the literature reveals no clear consensus on what counts as evidence against the hypothesis and no detailed analysis of why the facts of the sort cited constitute evidence one way or another. Unable to produce a well-developed argument one way or the other, some observers despair, retreating to unattractive fall-back positions, e.g., that the decision on whether or not V = L is a matter of personal aesthetics. I would prefer to avoid such conclusions, if possible. If we are to believe that L is not V, as so many would urge, then there ought to be good reasons for this belief, reasons that can be stated clearly and subjected to rational evaluation. Though no complete argument has been presented, the literature does contain a number of varied argument fragments, and it is worth asking whether some of these might be developed into a persuasive case.

One particularly simple approach would be to note that the existence of a measurable cardinal (MC) implies that V ≠ L,1 and to argue that there is a measurable cardinal. The drawback to this approach is that its implying V ≠ L cannot then be counted as evidence in favor of MC, as it often is. Indeed, there seems to have been considerable sentiment against V = L even before the proof of its negation from MC,2 and this sentiment must either be accounted for as reasonable or explained away as an aberration of some kind.

By ℬ2 we denote the σ-ideal of all subsets A of the Cantor set {0, 1}ω such that for every infinite subset T of ω the restriction A∣{0, 1}T is a proper subset of {0, 1}T. In this paper we investigate set theoretical properties of this and similar ideals.

The study of filters on Pκλ started by Jech [5] as a natural generalization of that of filters on an uncountable regular cardinal κ. Several notions including weak normality have been generalized. However, there are two versions proposed as weak normality for filters on Pκλ. One is due to Abe [1] as a straightforward generalization of weak normality for filters on κ due to Kanamori [6] and the other is due to Mignone [8]. While Mignone's version is weaker than normality, Kanamori-Abe's version is not in general. In fact, Abe [2] has proved, generalizing Kanamori [6], that a filter is weakly normal in the sense of Abe iff it is weakly normal in the sense of Mignone and there exists no disjoint family of cfλ-many positive sets. Therefore Kanamori-Abe's version is essentially a large cardinal property and Mignone's version seems to be the most natural formulation of “weak” normality.

In this paper, we study weak normality in the sense of Mignone. In [8], Mignone studies weak normality of canonically defined filters. We complement his chart and try to find the weakly normal closures of these filters (i.e., the minimal weakly normal filters extending them). Therefore our result is a natural refinement of Carr [4].

It is now well known that combinatorics on Pκλ is not a naive generalization of that on κ. For example, Menas [7] showed that stationarity on Pκλ can be characterized by 2-dimensional regressive functions, but not by 1-dimensional ones when λ is strictly larger than κ. We show in terms of weak normality that combinatorics on Pκλ vary drastically with respect to cfλ.

We study the strength (over bounded induction) of axioms expressing particular cases of the Chinese Remainder Theorem with respect to the axiom ∀x, y∃z (z = xy).

We build models where all -sets of reals are measurable and (or) have the property of Baire and (or) are Ramsey. We will show that there is no implication between any of these properties for -sets of reals.

Let be an admissible set. A sentence of the form is a sentence if φ ∈ (φ is ∨ Φ where Φ is an -r.e. set of sentences from ). A sentence of the form is an , sentence if φ is a sentence. A class of structures is, for example, a ∀1 class if it is the class of models of a ∀1() sentence. Thus ∀1() is a class of classes of structures, and so forth.

Let i, be the structure 〈i, <〉, for i > 0. Let Γ be a class of classes of structures. We say that a sequence J1, …, Ji,…, i < ω, of classes of structures is a Γ sequence if Ji ∈ Γ, i < ω, and there is I ∈ Γ such that ∈ Ji, if and only if [],i, where [,] is the disjoint sum. A class Γ of classes of structures has the easy uniformization property if for every Γ sequence J1,…, Ji,…, i < ω, there is a Γ sequence J′t, …, J′i, …, i < ω, such that J′i ⊆ Ji, i < ω, ⋃J′i = ⋃Ji, and the J′i are pairwise disjoint. The easy uniformization property is an effective version of Kuratowski's generalized reduction property that is closely related to Moschovakis's (topological) easy uniformization property.

We show over countable structures that ∀1() and ∃2() have the easy uniformization property if is a countable admissible set with an infinite member, that and have the easy uniformization property if α is countable, admissible, and not weakly stable, and that and have the easy uniformization properly. The results proved are more general. The result for answers a question of Vaught(1980).

We shall present two novel ways of deriving simply typed combinatory models. These are of interest in a constructive setting. First we look at extension models, which are certain subalgebras of full function space models. Then we shall show how the space of singletons of a combinatory model can itself be made into one. The two and the algebras in between will have many common features. We use these two constructions in proving:

Suppose κ is a supercompact cardinal and λ > κ. We study the relationship between the partition properly and the weak partition properly for normal ultrafilters on Pκλ. On the one hand, we show that the following statement is consistent, given an appropriate large cardinal assumption: The partition property and the weak partition properly are equivalent, there are many normal ultrafilters that satisfy these properties, and there are many normal ultrafilters that do not satisfy these properties. On the other hand, we consider the assumption that, for some λ > κ, there exists a normal ultrafilter U on Pκλ such that U satisfies the weak partition property but does not satisfy the partition property. We show that this assumption is implied by the assertion that there exists a cardinal γ > κ such that γ is γ+-supercompact, and, assuming the GCH, it implies the assertion that there exists a cardinal γ > κ such that γ is a measurable cardinal with a normal ultrafilter concentrating on measurable cardinals.

We consider the existence of coherent families of finite-to-one functions on countable subsets of an uncountable cardinal κ. The existence of such families for κ implies the existence of a winning 2-tactic for player TWO in the countable-finite game on κ. We prove that coherent families exist on κ = ωn, where n ∈ ω, and that they consistently exist for every cardinal κ. We also prove that iterations of Axiom A forcings with countable supports are Axiom A.

An old conjecture of modal logics states that every splitting of the major systems K4, S4, G and Grz has the finite model property. In this paper we will prove that all iterated splittings of G have fmp, whereas in the other cases we will give explicit counterexamples. We also introduce a proof technique which will give a positive answer for large classes of splitting frames. The proof works by establishing a rather strong property of these splitting frames namely that they preserve the finite model property in the following sense. Whenever an extension Λ has fmp so does the splitting Λ/f of Λ by f. Although we will also see that this method has its limitations because there are frames lacking this property, it has several desirable side effects. For example, properties such as compactness, decidability and others can be shown to be preserved in a similar way and effective bounds for the size of models can be given. Moreover, all methods and proofs are constructive.

One of the main theorems of the paper states the following. Let R-K-M be finite extensions of a rational one variable function field R over a finite field of constants. Let S be a finite set of valuations of K. Then the ring of elements of K having no poles outside S has a Diophantine definition over its integral closure in M.

A first-order sentence Φ is Σ2 if there is a quantifier-free formula Θ such that Φ has the form . The Σ2-theory of a structure for a language ℒis the set of Σ2-sentences of ℒ true in . It was shown independently by Lerman and Shore (see [Le, Theorem VII.4.4]) that the Σ2-theory of the structure = 〈D, ≤ 〉 is decidable, where D is the set of degrees of unsolvability and ≤ is the standard ordering of D. This result is optimal in the sense that the Σ3-theory of is undecidable, a result due to J. Schmerl. (For a proof, see [Le, Theorem VII.4.5]. As Lerman has pointed out, this proof should be corrected by defining θσ to be ∀xσ1(x) rather than ∀x(ψ(x)→ σ1(x)).) Nonetheless, in this paper we extend the decidability result of Lerman and Shore by showing that the Σ2-theory of is decidable, where ⋃ is the least upper bound operator and 0 is the least degree. Of course ⋃ is definable in , but many interesting degree-theoretic results are expressible as Σ2-sentences in the language of ∪ but not as Σ2-sentences in the language of . For instance, Simpson observed that the Posner-Robinson cupping theorem could be used to show that for any nonzero degrees a, b, there is a degree g such that b ≤ a ⋃ g, and b ⋠ g (see [PR, Corollary 6]). However, the Posner-Robinson technique does not seem to suffice to decide the Σ2-theory of ∪. We introduce instead a new method for coding a set into the join of two other sets and use it to decide this theory.

For a ring with unit R, which need not be associative, denote the group of upper unitriangular 3 × 3 matrices over R by UT3(R). Let e1 = (1,0,0), e2 = (0,1,0), where (α, β, γ) denotes the matrix

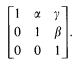
Denote the expanded group (UT3(R), e1, e2) by 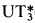(R). A. 1. Mal′cev [M] gave an algebraic characterization of the expanded groups of the form 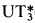(R) as follows. Let h1, h2 be elements of a group H; then (H, h1, h2) is isomorphic to 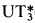(R), for some R, if and only if

(i) H is 2-step nilpotent;

(ii) CH(hi) are abelian, i = 1,2;

(iii) CH(h1) ∩ CH(h2) = Z(H);

(iv) [CH(h1),h2] = [h1, CH(h2)] = Z(H);

(v) Z(H) is a direct summand in both CH(hi).

(In [M] condition (v) is a bit stronger; the version above is presented in [B2].)

A pair (h1, h2) of elements of a group H is said to be a base if (H, h1, h2) satisfies the conditions (i)–(iv). A. I. Mal′cev [M] found a uniform way of first order interpreting a ring Ring(H, h1, h2) in any group with a base (H, h1, h2); in particular, Ring(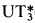(R)) ≃ R.

The notions of forcing and generic set were introduced by Cohen in 1963 to prove the independence of the Axiom of Choice and the Continuum Hypothesis in set theory. Let ω be the set of natural numbers, i.e., {0,1,2,3,…}. A string is a mapping from an initial segment of ω into {0,1}. We identify a set A ⊆ ω to with its characteristic function.

We now consider a set generic over the arithmetic sets. A set A ⊆ ω is called n-generic if it is Cohen-generic for n-quantifier arithmetic. This is equivalent to saying that for every -set of strings S, there is a σ ⊂ A such that σ ∈ S or (∀v ≥ σ)(v ∉ S). By degree we mean Turing degree (of unsolvability). We call a degree n-generic if it has an n-generic representative. For a degree a, let D(≤a) denote the set of degrees which are recursive in a.

Before Cohen's work, there was a precursor of the notion of forcing in recursion theory. Friedberg showed that for every degree b above the complete degree 0', i.e., the degree of a complete r.e. set, there is a degree a such that a′ = a ⋃ 0′ = b. He actually proved this result by using the notion of forcing for statements.

Galois theory states that if L is a certain algebraic extension (called a Galois extension) of a field K, then there is a one-to-one correspondence (called a Galois correspondence) between subfields M, K ⊂ M ⊂ L and subgroups of the automorphism groups of L fixing the elements in K.

A subfield of a field L can be considered as a substructure of L in general model theory. However, a substructure is a subset closed under functions which are interpretations of function symbols in a given language, so the notion of substructure may change if we expand the language by adding definable notions. On the other hand a definably closed substructure is a subset which is closed under all definable functions, and it does not change by such expansions. If we are interested in subfields of an algebraically closed field of characteristic 0, these two notions are the same. But in a field of prime characteristic they are not equal. Speaking roughly, a Galois extension of a field K is an extension whose subfields are relatively definably closed. Poizat [4] showed that if a structure M has elimination of imaginaries there is a kind of Galois correspondence between definably closed substructures and subgroups of bijective elementary mappings of M.

In this paper, using Poizat's result we study algebraic types. As is well known, one motivation for developing the Galois theory was to show the unsolvability of equations with degree ≥ 5. We want to take this unsolvability as a special case of general phenomena. For this purpose, we introduce several notions which are stronger than mere algebraicity and study relations between these notions and groups of bijective elementary mappings. (See Theorems 3.7 and 3.9.)

In his paper [7] Steel asked whether there can exist a normal measure U on a cardinal κ such that

We use Reverse Easton forcing to show that this is consistent from a P2κ hypermeasure; we also show that the result is sharp, using the core model for nonoverlapping coherent extender sequences.

The proof uses forcing technology due to Woodin.

In this section we collect some facts that are useful in the forcing constructions of the next section. None of them are due to us, and we are unsure to whom they should be attributed for the most part. We give sketchy proofs; the reader who wants to see more details is referred to [2].

PA is Peano Arithmetic. Pr(x) is the usual Σ1,-formula representing provability in PA. A strong provability predicate is a formula which has the same properties as Pr(·) but is not Σ1. An example: Q is ω-provable if PA + ¬Q is ω-inconsistent (Boolos [4]). In [5] Dzhaparidze introduced a joint provability logic for iterated ω-provability and obtained its arithmetical completeness.

In this paper we prove some further modal properties of Dzhaparidze's logic, e.g., the fixed point property and the Craig interpolation lemma. We also consider other examples of the strong provability predicates and their applications.

Inductive definability has been studied for some time already. Nonetheless, there are some simple questions that seem to have been overlooked. In particular, there is the problem of the expressibility of the μ-calculus.

The μ-calculus originated with Scott and DeBakker [SD] and was developed by Hitchcock and Park [HP], Park [Pa], Kozen [K], and others. It is a language for including inductive definitions with first-order logic. One can think of a formula in first-order logic (with one free variable) as defining a subset of the universe, the set of elements that make it true. Then “and” corresponds to intersection, “or” to union, and “not” to complementation. Viewing the standard connectives as operations on sets, there is no reason not to include one more: least fixed point.

There are certain features of the μ-calculus coming from its being a language that make it interesting. A natural class of inductive definitions are those that are monotone: if X ⊃ Y then Γ (X) ⊃ Γ (Y) (where Γ (X) is the result of one application of the operator Γ to the set X). When studying monotonic operations in the context of a language, one would need a syntactic guarantor of monotonicity. This is provided by the notion of positivity. An occurrence of a set variable S is positive if that occurrence is in the scopes of exactly an even number of negations (the antecedent of a conditional counting as a negation). S is positive in a formula ϕ if each occurrence of S is positive. Intuitively, the formula can ask whether x ∊ S, but not whether x ∉ S. Such a ϕ can be considered an inductive definition: Γ (X) = {x ∣ ϕ(x), where the variable S is interpreted as X}. Moreover, this induction is monotone: as X gets bigger, ϕ can become only more true, by the positivity of S in ϕ. So in the μ-calculus, a formula is well formed by definition only if all of its inductive definitions are positive, in order to guarantee that all inductive definitions are monotone.

Recent work in natural language semantics leads to some new observations on generalized quantifiers. In §1 we show that English quantifiers of type 〈1, 1〉 are booleanly generated by their generalized universal and generalized existential members. These two classes also constitute the sortally reducible members of this type.

Section 2 presents our main result — the Generalized Prefix Theorem (GPT). This theorem characterizes the conditions under which formulas of the form (Q1x1…QnxnRx1…xn and q1x1…qnxnRx1…xn are logically equivalent for arbitrary generalized quantifiers Qi, qi. GPT generalizes, perhaps in an unexpectedly strong form, the Linear Prefix Theorem (appropriately modified) of Keisler & Walkoe (1973).