Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T18:44:19.626Z Has data issue: false hasContentIssue false
  • English
  • Français

On the compactness of ℵ1 and ℵ2

Published online by Cambridge University Press:  12 March 2014

C. A. di Prisco  and
J. Henle
C. A. di Prisco
Affiliation:
Instttuto Venezolano de Investigaciones Científicas, Caracas, Venezuela
J. Henle
Affiliation:
Massachusetts Institute of Technology, Cambridge, MA 02139
Get access Rights & Permissions [Opens in a new window]

Extract

In recent years, the Axiom of Determinateness (AD) has yielded numerous results concerning the size and properties of the first ω-many uncountable cardinals. Briefly, these results began with Solovay's discovery that ℵ1 and ℵ2 are measurable [8], [3], continued with theorems of Solovay, Martin, and Kunen concerning infinite-exponent partition relations [6], [3], Martin's proof that ℵn has confinality ℵ2 for 1 < n < ω, and very recently, Kleinberg's proof that the ℵn are Jonsson cardinals [4].

This paper was inspired by a very recent result of Martin from AD that ℵ1 is ℵ2-super compact. It was known for some time that AD implies ℵ1 is α-strongly compact for all ℵ < θ (where θ is the least cardinal onto which 2ω cannot be mapped, quite a large cardinal under AD), and that ADR implies that ℵ1, is α-super compact for all α < θ. A key open question had been whether or not ℵ1 is super compact under AD alone.

This paper comments on the method of Martin in several different ways. In §2, we will prove that ℵ1 is ℵ2-super compact, and then generalize the method to show that ℵ2 is ℵ3-strongly compact. In addition, we will demonstrate a limitation in the method by showing that the possible measures obtained on 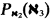are not normal, and that the method cannot be extended to show that ℵ2 is ℵ4-strongly compact.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 3 , September 1978 , pp. 394 - 401
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Di Prisco, C., Combinatorial properties and supercompact cardinals, Doctoral Dissertation, M.I.T., 1976.Google Scholar
[2]Jech, T., Some combinatorial problems concerning uncountable cardinals, Annals of Mathematical Logic, vol. 5 (1973), pp. 165–198.CrossRefGoogle Scholar
[3]Kechris, A., Notes prepared for the M.I.T. Logic Seminar, 1972–1973.Google Scholar
[4]Kleinberg, E. M., AD ⊦ ‘The ℵ1 are Jonsson Cardinals and ℵω is a Rowbottom Cardinal’, Annals of Mathematical Logic (to appear).Google Scholar
[5]Magidor, M., Combinatorial characterization of supercompact cardinals, Proceedings of the American Mathematical Society, vol. 42 (1974), pp. 279–285.CrossRefGoogle Scholar
[6]Martin, D. A., Determinateness implies many cardinals are measurable, mimeographed.Google Scholar
[7]Menas, T. K., On strong compactness and super compactness, Doctoral Dissertation, University of California, Berkeley.Google Scholar
[8]Solovay, R. M., Measurable cardinals and the axiom of determinateness, Lecture notes prepared in connection with the Summer Institute of Axiomatic Set Theory held at U.C.L.A., Summer, 1967.Google Scholar