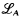Given I, a reasonable countable set of Turing degrees, can we find some sort of canonical strict upper bound on I? If I = {a ∣ a ≤ b}, the upper bound on I which springs to mind is b′. But what if I is closed under jump? This question arises naturally out of the question which motivates a large part of hierarchy theory: Is there a canonical increasing function from a countable ordinal, preferably a large one, into D, the set of Turing degrees? If d is to be such a function, it is natural to require that d(α + 1) = d(α)′; but how should d(λ) depend on d ↾ λ, where λ is a limit ordinal?
For any I ⊆ D, let MI, = ⋃I. Towards making the above questions precise, we introduce ideals of Turing degrees.
Definition 1. I ⊆ D is an ideal iff I is closed under jump and join, and I is downward-closed, i.e., if a ≤ b & b ϵ I then a ϵ I.
The following definition reflects the hierarchy-theoretic motivation for this paper.
Definition 2. For I ⊆ D and A ⊆ ω, I is an A-hierarchy ideal iff for some countable ordinal α, MI = Lα[A]∩ ωω.
All hierarchy ideals are ideals, but not conversely.
Early in the game Spector knocked out the best sort of canonicity for upper bounds on ideals, proving that no set of degrees closed under jump has a least upper bound.
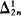 -degrees
-degrees