Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-31T07:24:40.239Z Has data issue: false hasContentIssue false
  • English
  • Français

TREES AND STATIONARY REFLECTION AT DOUBLE SUCCESSORS OF REGULAR CARDINALS

Part of: Set theory

Published online by Cambridge University Press:  14 February 2022

THOMAS GILTON ,
MAXWELL LEVINE  and
ŠÁRKA STEJSKALOVÁ Open the ORCID record for ŠÁRKA STEJSKALOVÁ [Opens in a new window]
THOMAS GILTON*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF PITTSBURGH 166 THACKERAY AVENUE PITTSBURGH, PA 15213, USA
MAXWELL LEVINE
Affiliation:
INSTITUTE OF MATHEMATICS UNIVERSITY OF FREIBURG ERNST-ZERMELO-STRASSE 1 FREIBURG IM BREISGAU 79104, GERMANY E-mail: maxwell.levine@mathematik.uni-freiburg.de
ŠÁRKA STEJSKALOVÁ
Affiliation:
DEPARTMENT OF LOGIC CHARLES UNIVERSITY CELETNÁ 20, 116 42 PRAGUE 1, CZECH REPUBLIC E-mail: sarka.stejskalova@ff.cuni.cz
*
E-mail: tdg25@pitt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain an array of consistency results concerning trees and stationary reflection at double successors of regular cardinals 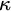$\kappa $, updating some classical constructions in the process. This includes models of 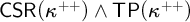$\mathsf {CSR}(\kappa ^{++})\wedge {\sf TP}(\kappa ^{++})$ (both with and without 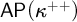${\sf AP}(\kappa ^{++})$) and models of the conjunctions 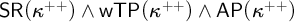${\sf SR}(\kappa ^{++}) \wedge \mathsf {wTP}(\kappa ^{++}) \wedge {\sf AP}(\kappa ^{++})$ and 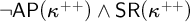$\neg {\sf AP}(\kappa ^{++}) \wedge {\sf SR}(\kappa ^{++})$ (the latter was originally obtained in joint work by Krueger and the first author [9], and is here given using different methods). Analogs of these results with the failure of 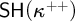$\sf {SH}(\kappa ^{++})$ are given as well. Finally, we obtain all of our results with an arbitrarily large 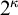$2^\kappa $, applying recent joint work by Honzik and the third author.

Keywords

forcingtree propertystationary reflectionclub stationary reflectionsuslin treesapproachability

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E35: Consistency and independence results 03E55: Large cardinals

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 2 , June 2023 , pp. 780 - 810
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abraham, U., Aronszajn trees on  ${\aleph}_2$  and  ${\aleph}_3$ . Annals of Pure and Applied Logic, vol. 24 (1983), no. 3, pp. 213–230.CrossRefGoogle Scholar
Baumgartner, J., Iterated forcing , Surveys in Set Theory (Mathias, A., editor), London Mathematical Society Lecture Notes Series, vol. 87, Cambridge University Press, Cambridge, 1983, pp. 1–59.Google Scholar
Cummings, J., Notes on singular cardinal combinatorics . Notre Dame Journal of Formal Logic, vol. 46 (2005), no. 3, pp. 251–282.CrossRefGoogle Scholar
Cummings, J., Iterated forcing and elementary embeddings , Handbook of Set Theory, vol. 2 (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 885–1148.Google Scholar
Cummings, J. and Foreman, M., The tree property . Advances in Mathematics, vol. 133 (1998), no. 1, pp. 1–32.10.1006/aima.1997.1680CrossRefGoogle Scholar
Cummings, J., Friedman, S.-D., Magidor, M., Rinot, A., and Sinapova, D., The eightfold way, this Journal, vol. 83 (2018), no. 1, pp. 349–371.Google Scholar
Devlin, K. J., ℵ 1-trees . Annals of Mathematical Logic, vol. 13 (1978), no. 3, pp. 267–330.CrossRefGoogle Scholar
Devlin, K. J., Constructibility. Perspectives in Mathematical Logic , Springer, Berlin, 1984.CrossRefGoogle Scholar
Gilton, T. and Krueger, J., A note on the eightfold way . Proceedings of the American Mathematical Society, vol. 148 (2020), no. 3, pp. 1283–1293.10.1090/proc/14771CrossRefGoogle Scholar
Gilton, T. D., On the infinitary combinatorics of small cardinals and the cardinality of the continuum , Ph.D. thesis, University of California, Los Angeles, 2019.Google Scholar
Gitik, M. and Krueger, J., Approachability at the second successor of a singular cardinal, this Journal, vol. 74 (2009), no. 4, pp. 1211–1224.Google Scholar
Hamkins, J. D., A class of strong diamond principles, preprint, 2002, arXiv:math/0211419.Google Scholar
Harrington, L. and Shelah, S., Some exact equiconsistency results in set theory . Notre Dame Journal of Formal Logic, vol. 26 (1985), no. 2, pp. 178–188.CrossRefGoogle Scholar
Holy, P., Lücke, P., and Njegomir, A., Small embedding characterizations for large cardinals . Annals of Pure and Applied Logic, vol. 170 (2019), no. 2, pp. 251–271.10.1016/j.apal.2018.10.002CrossRefGoogle Scholar
Honzik, R. and Stejskalová, Š.. Small  $u\left(\kappa \right)$  at singular with compactness at  ${\kappa}^{++}$ . Archive for Mathematical Logic, vol. 61 (2022), pp. 33–54.CrossRefGoogle Scholar
Jech, T., Set Theory, 3rd ed., Springer, Berlin, 2003.Google Scholar
Kunen, K., Saturated ideals, this Journal, vol. 43 (1978), no. 1, pp. 65–76.Google Scholar
Laver, R., Making the supercompactness of  $\kappa$  indestructible under  $\kappa$  directed closed forcing . Israel Journal of Mathematics, vol. 29 (1978), no. 4, pp. 385–388.CrossRefGoogle Scholar
Magidor, M., Reflecting stationary sets, this Journal, vol. 47 (1982), no. 4, pp. 755–771.Google Scholar
Mitchell, W. J., Aronszajn trees and the independence of the transfer property . Annals of Mathematical Logic, vol. 5 (1972), no. 1, pp. 21–46.CrossRefGoogle Scholar
Rinot, A., Higher Souslin trees and the GCH, revisited . Advances in Mathematics, vol. 311 (2017), pp. 510–531.CrossRefGoogle Scholar
Rinot, A.. On the ideal $J[\kappa]$ . Annals of Pure and Applied Logic , vol. 173 (2022), no. 2, 103055.Google Scholar
Solovay, R. M., A model of set theory in which every set of reals is Lebesgue measurable . Annals of Mathematics, vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar
Todorčević, S., Partitioning pairs of countable ordinals . Acta Mathematica, vol. 159 (1987), nos. 3–4, pp. 261–294.CrossRefGoogle Scholar
Unger, S., Fragility and indestructibility of the tree property . Archive for Mathematical Logic, vol. 51 (2012), nos. 5–6, pp. 635–645.CrossRefGoogle Scholar
Unger, S., Fragility and indestructibility II . Annals of Pure and Applied Logic, vol. 166 (2015), no. 11, pp. 1110–1122.CrossRefGoogle Scholar