Uncountable models and infinitary elementary extensions

Extract

Let A be a countable admissible set (as defined in [1], [3]). The language L_A consists of all infinitary finite-quantifier formulas (identified with sets, as in [1]) that are elements of A. Notationally, L_A = A ∩ L_ω1ω. Then L_A is a countable subset of L_ω1ω, the language of all infinitary finite-quantifier formulas with all conjunctions countable. The set 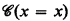is the set of L_ω1ω sentences defined in 2.2 below. The following theorem characterizes those A-Σ₁ sets Φ of L_A sentences that have uncountable models.

Main Theorem (3.1.). If Φ is an A-Σ₁set of L_A sentences, then the following are equivalent:

(a) Φ has an uncountable model,

(b) Φ has a model with a proper L_A-elementary extension,

(c) for every 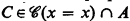, ⋀Φ → C is not valid.

This theorem was announced in [2] and is proved in §§3, 4, 5. Makkai's earlier [4, Theorem 1] implies that, if Φ determines countable structure 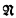up to L_ω1ω-elementary equivalence, then (a) is equivalent to (c′) for all 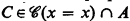, ⋀Φ → C is not valid.

The requirement in 3.1 that Φ is A-Σ₁ is essential when the set ω of all natural numbers is an element of A. For by the example of [2], then there is a set Φ L_A sentences such that (b) holds and (a) fails; it is easier to show that, if ω ϵ A, there is a set Φ of L_A sentences such that (c) holds and (b) fails.