Article contents
Vicious circle principle and the paradoxes
Published online by Cambridge University Press: 12 March 2014
Extract
This note is a sequel to the previous paper of mine which was entitled Identity, variables, and impredicative definitions and published in this Journal, vol. 21 (1956), pp. 225–245. That early paper served to call attention to the dependency of the set-theoretic paradoxes on the interpretation of the variables that may occur in the critical abstraction principle:

where K is a well-formed formula containing free occurrences of y but not those of x.
A partial reinterpretation of the variables occurring in the above formalization of the abstraction principle yields Frege's unsuccessful way out of Russell's antinomy:
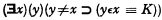
with the same kind of K as above. Another gives us the alternative schema
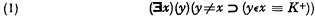
where K+ is obtained from a K of the kind described above by replacing every well-formed part of the form (∃z)L by (∃z)(z≠x & L) and every well-formed part of the form (z)L by (z)(z≠x ⊃ L). Still a third choice of an interpretation yields the schema
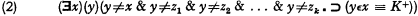
where K+ is subject to the same conditions as in (1) and z1, z2, …, zk are all the free variables of (2). These three interpretations are only some of the most conspicuous ones among a multitude of possible ways of interpreting the variables that may occur in the abstraction principle.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1957
References
1 I am indebted to Mr. Elliott Mendelson for suggesting a number of simplifications in this part of the proof.
- 11
- Cited by

