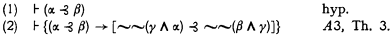In this paper we show how a modification of results due to Simons ([6]) yields a set of independent axiom schemata for von Wright's M ([8], p. 85), with a single primitive rule of inference. We first describe a system M*, then show its equivalence with M, and finally show that our schemata are independent.
1. Axiomatization ofM*. We adopt the notational conventions of McKinsey and Tarski ([4], p. 2), as amended by Simons ([6], p. 309), except that we take “(α ⊰ β)” as an abbreviation for “˜◇˜(α 0→ β)”, rather than for “˜◇(α ∧ ˜β)”. Our only rule of inference is:
Rule. If ⊦ α and ⊦ (˜◇˜α → β). then ⊦ β.
We have six axiom schemata:
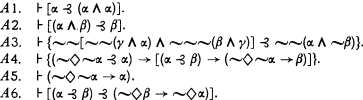
We require a number of theorems for the proof of equivalence of M* with M.
Theorem 1. If ⊦ α and ⊦ (α → β), then ⊦ β.
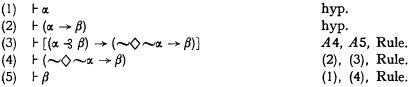
Theorem 2. If ⊦ α and ⊦ (α ⊰ β), then ⊦ β.
Proof by hypothesis, A5, and Theorem 2 (twice).
Theorem 3. If ⊦ (α ⊰ β), then (˜◇β → ˜ ◇α).
Proof by hypothesis, A6, and Theorem 2.
Theorem 4. If ⊦(α ⊰ β), then ⊦[˜˜(γ ∧ α) ⊰ ˜˜(β ∧ γ)].