In this paper we present a normalization theorem for a natural deduction formulation of Zermelo set theory. Our result gets around M. Crabbe's counterexample to normalizability (Hallnäs [3]) by adding an inference rule of the form

and requiring that this rule be used wherever it is applicable. Alternatively, we can regard the result as pertaining to a modified notion of normalization, in which an inference

is never considered reducible if A is T Є T, even if R is an elimination rule and the major premise of R is the conclusion of an introduction rule. A third alternative is to regard (1) as a derived rule: using the general well-foundedness rule

we can derive (1). If we regard (2) as neutral with respect to the normality of derivations (i.e., (2) counts as neither an introduction nor an elimination rule), then the resulting proofs are normal.

In this paper we solve some of Pál Erdős's favorite problems on uncountably chromatic graphs. Generalizing a finite graph theory result of Tutte, Erdős and R. Rado showed that for every infinite cardinal κ there exists a triangle-free, κ-chromatic graph of size κ. For κ = ℵ0, Erdős established the existence of ℵ0-chromatic graphs excluding even C4, C5,…, Cn, i.e. circuits up to a given length. For κ < ℵ0 the situation is different. As shown by Erdős and A. Hajnal, a graph is necessarily countably chromatic if it omits any finite bipartite graph. We can, however, exclude any finite list of nonbipartite graphs (this obviously reduces to excluding finitely many odd circuits). They posed an even stronger conjecture, namely, that similar examples must occur in every uncountably chromatic graph. To be specific, they conjectured that for every infinite κ, every κ-chromatic graph contains a κ-chromatic triangle-free subgraph. Here we show that this may not be true for κ = ℵ1 i.e. we exhibit a model where it is false. We must emphasize that the conjecture is probably false already in ZFC, but we have been unable to show this.

The topic of this paper is jump operators, a subject which originated with some questions of Martin and a partial answer to them obtained by Steel [18]. The topic of jump operators is a part of the general study of the structure of the Turing degrees, but it is concerned with an aspect of that structure which is different from the usual concerns of classical recursion theory. Specifically, it is concerned with studying functions on the degrees, such as the Turing jump operator, the hyperjump operator, and the sharp operator.

Roughly speaking, a jump operator is a definable ≤T-increasing function on the Turing degrees. The purpose of this paper is to characterize the jump operators, in terms of concepts from descriptive set theory. Again roughly speaking, the main theorem states that all jump operators (other than the identity function) are obtained from pointclasses by the same process by which the hyperjump operator is obtained from the pointclass Π11; that is, if Γ is the pointclass, then the operator maps the real x to the universal Γ(x) subset of ω. This characterization theorem has some corollaries, one of which answers a question of Steel [18]. In §1 we give a brief introduction to this general topic, followed by a brief (and still somewhat imprecise) description of the results contained in this paper.

The aim of this paper is to characterize varieties of Heyting algebras with decidable theory of their finite members. Actually we prove that such varieties are exactly the varieties generated by linearly ordered algebras. It contrasts to the result of Burris [2] saying that in the case of whole varieties, only trivial variety and the variety of Boolean algebras have decidable first order theories.

This is a continuation of Believing the axioms. I, in which nondemonstrative arguments for and against the axioms of ZFC, the continuum hypothesis, small large cardinals and measurable cardinals were discussed. I turn now to determinacy hypotheses and large large cardinals, and conclude with some philosophical remarks.

Determinacy is a property of sets of reals. If A is such a set, we imagine an infinite game G(A) between two players I and II. The players take turns choosing natural numbers. In the end, they have generated a real number r (actually a member of the Baire space ωω). If r is in A, I wins; otherwise, II wins. The set A is said to be determined if one player or the other has a winning strategy (that is, a function from finite sequences of natural numbers to natural numbers that guarantees the player a win if he uses it to decide his moves).

Determinacy is a “regularity” property (see Martin [1977, p. 807]), a property of well-behaved sets, that implies the more familiar regularity properties like Lebesgue measurability, the Baire property (see Mycielski [1964] and [1966], and Mycielski and Swierczkowski [1964]), and the perfect subset property (Davis [1964]). Infinitary games were first considered by the Polish descriptive set theorists Mazur and Banach in the mid-30s; Gale and Stewart [1953] introduced them into the literature, proving that open sets are determined and that the axiom of choice can be used to construct an undetermined set.

This paper continues the project initiated in [5]: a model-theoretic study of the concept of cardinality within certain higher-order logics. As recommended by an editor of this Journal, I will digress to say something about the project's motivation. Then I will review some of the basic definitions from [5]; for unexplained notation the reader should consult [5].

The syntax of ordinary usage (with respect to the construction of arguments as well as the construction of individual sentences) makes it natural to classify numerals and expressions of the form ‘the number of F's’ as singular terms, expressions like ‘is prime’ or ‘is divisible by’ as predicates of what Frege called “level one”, and expressions like ‘for some natural number’ as first-order quantifier-phrases. From this syntatic classification, it is a short step—so short as to be frequently unnoticed—to a semantic thesis: that such expressions play the same sort of semantic role as is played by the paradigmatic (and nonmathematical) members of these lexical classes. Thus expressions of the first sort are supposed to designate objects (in post-Fregean terms, entities of type 0), those of the second sort to be true or false of tuples of objects, and those of the third sort to quantify over objects. All this may be summed up in Frege's dictum: “Numbers are objects.”

Let L be one of the topological languages Lt, (L∞ω)t and (Lκω)t. We characterize the topological spaces which are models of the L-theory of the class of ordinals equipped with the order topology. The results show that the role played in classical model theory by the property of being well-ordered is taken over in the topological context by the property of being locally compact and scattered.

As a contribution to definability theory in the spirit of Tarski's classical work on (R, <, 0, 1, +, ·) we extend here part of his results to the structure

Here exp ∣[0, 1] and sin ∣[0, π] are the restrictions of the exponential and sine function to the closed intervals indicated; formally we identify these restricted functions with their graphs and regard these as binary relations on R. The superscript “RE” stands for “restricted elementary” since, given any elementary function, one can in general only define certain restrictions of it in RRE.

Let (RRE, constants) be the expansion of RRE obtained by adding a name for each real number to the language. We can now formulate our main result as follows.

Theorem. (RRE, constants) is strongly model-complete.

This means that every formula ϕ(X1, …, Xm) in the natural language of (RRE, constants) is equivalent to an existential formula

with the extra property that for each x ∈ Rm such that ϕ(x) is true in RRE there is exactly one y ∈ Rn such that ψ(x, y) is true in RRE. (Here ψ is quantifier free.)

It is shown that if κ is an uncountable successor cardinal in L[0#], then there is a normal tree T ϵ L[0#] of height κ such that 0# ∉ L[T], yet T is < κ-distributive in L[0#]. A proper class version of this theorem yields an analogous L[0#]-definable tree such that distinct branches in the presence of 0# collapse the universe. A heretofore unutilized method for constructing in L[0#] generic objects for certain L-definable forcings and “exotic sequences”, combinatorial principles introduced by C. Gray, are used in constructing these trees.

Ordinary equational logic is a connective-free fragment of first-order logic which is concerned with total functions under the relation of ordinary equality. In [AN] (see also [AN1]) and in [Cr] it has been extended in two equivalent ways into a near-equational system of logic for partial functions. The extension given in [Cr] deals with partial functions under two relationships: a relationship of existence-dependent existence and one of existence-dependent Kleene equality. For the language that involves both relationships a set of rules was given that is complete. Those rules in the set that involve only existence-dependent existence turned out to be complete for the sublanguage that involves this relationship only. In the present paper we give a set of rules that is complete for the other sublanguage, namely the language of partial functions under existence-dependent Kleene equality.

This language lacks a certain, often needed, power of expressing existence and fails, in particular, to be an extension of the language that underlies ordinary equational logic. That it possesses a fairly simple complete set of rules is therefore perhaps more of theoretical than of practical interest. The present paper is thus intended to serve as a supplement to [Cr] and, less directly, to [AN]. The subject is further rounded out, and some contrast is provided, by [Rob]. The systems of logic treated there are based on the weaker language in which partial functions are considered under the more basic relation of Kleene equality.

In Hilbert and Ackermann [2] there is a simple proof of the consistency of first order predicate logic by reducing it to propositional logic. Intuitively, the proof is based on interpreting predicate logic in a domain with only one element. Tarski [7] and Gentzen [1] have extended this method to simple type theory by starting with an individual domain consisting of a single element and then interpreting a higher type by the set of truth valued functions on the previous type.

I will use the method of Hilbert and Ackermann on Martin-Löf's type theory without universes to show that ¬Eq(A, a, b) cannot be derived without universes for any type A and any objects a and b of type A. In particular, this proves the conjecture in Martin-Löf [5] that Peano's fourth axiom (∀x ϵ N)¬ Eq(N, 0, succ(x)) cannot be proved in type theory without universes. If by consistency we mean that there is no closed term of the empty type, then the construction will also give a consistency proof by finitary methods of Martin-Löf's type theory without universes. So, without universes, the logic obtained by interpreting propositions as types is surprisingly weak. This is in sharp contrast with type theory as a computational system, since, for instance, the proof that every object of a type can be computed to normal form cannot be formalized in first order arithmetic.

This paper belongs to cylindric-algebraic model theory understood in the sense of algebraic logic. We show the existence of isomorphic but not lower base-isomorphic cylindric set algebras. These algebras are regular and locally finite. This solves a problem raised in [N 83] which was implicitly present also in [HMTAN 81]. This result implies that a theorem of Vaught for prime models of countable languages does not continue to hold for languages of any greater power.

In this paper the theory of the core model K is applied to study certain combinatorial principles. These principles concern the existence of families of almost disjoint functions. The first, the transversal hypothesis, is defined as follows.

Definition. The transversal hypothesis for κ, T(κ), is the following assertion:

There is a sequence 〈fν: ν < κ+〉 such that

(a) fν: κ → κ regressively for ν < κ+, and

(b) if ν < ξ < κ+, then there is γ < κ such that fν(α) ≠ fξ(α) whenever γ < α < κ.

T(κ) is a simple consequence of the Kurepa hypothesis for κ, i.e. the assertion, KH(κ), that there is a family F ⊂ P(κ) such that 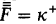and card({X ∩ α: X ϵ F}) ≤ α for ω < α < κ.

The second principle to be studied, the weak Kurepa hypothesis, is a statement of strength intermediate between the Kurepa and transversal hypotheses.

Definition. The weak Kurepa hypothesis for κ, wKH(κ), is the following assertion:

There is a sequence 〈bν: ν < κ+〉 such that

(a) bν ⊂ κ for ν < κ+, and

(b) for each limit λ < κ there is Fλ: {bν ∩ λ: ν < κ+} → λ such that setting fν(λ) = Fλ(bν ∩ λ) for ν < κ+ and limit λ < κ, if ν < ξ < κ+ there is γ < κ such that fν(λ) ≠ fξ(λ) whenever γ < λ < κ and λ is a limit.

The structure of the Turing degrees of generic and n-generic sets has been studied fairly extensively, especially for n = 1 and n = 2. The original formulation of 1-generic set in terms of recursively enumerable sets of strings is due to D. Posner [11], and much work has since been done, particularly by C. G. Jockusch and C. T. Chong (see [5] and [6]).

In the enumeration degrees (see definition below), attention has previously been restricted to generic sets and functions. J. Case used genericity for many of the results in his thesis [1]. In this paper we develop a notion of 1-generic partial function, and study the structure and characteristics of such functions in the enumeration degrees. We find that the e-degree of a 1-generic function is quasi-minimal. However, there are no e-degrees minimal in the 1-generic e-degrees, since if a 1-generic function is recursively split into finitely or infinitely many parts the resulting functions are e-independent (in the sense defined by K. McEvoy [8]) and 1-generic. This result also shows that any recursively enumerable partial ordering can be embedded below any 1-generic degree.

Many results in the Turing degrees have direct parallels in the enumeration degrees. Applying the minimal Turing degree construction to the partial degrees (the e-degrees of partial functions) produces a total partial degree ae which is minimal-like; that is, all functions in degrees below ae have partial recursive extensions.

A conservative extension of first order logic, suitable for circumscriptive inference, is introduced.

This note arose out of my efforts to understand results of van den Dries, Denef, and Weispfenning on definable Skolem functions in the elementary theory of Qp. The first person to prove their existence was van den Dries, who devised and applied a model-theoretic criterion for theories, admitting elimination of quantifiers, which also admit definable Skolem functions [3]. The proof, though elegant, does not describe how one defines the Skolem functions. In the particular case of Qp, Denef found an ingenious, easily described method for writing out the definitions [2, pp. 14–15]. Unfortunately, his argument directly applies only in the following special case: if

and there is a fixed m ≥ 1 such that

for all , then can be given as a definable function of . While this special case includes many of interest, van den Dries' theorem seems more general. Weispfenning suggested how his results on primitive-recursive quantifier elimination could produce algorithms yielding definitions of Skolem functions in the specific theories van den Dries considered [10, pp. 470–471]. Though these algorithms provide a more concrete version of van den Dries' theorem, and do not suffer the lack of generality of Denef's result, Weispfenning's argument is extremely subtle and applies only to certain theories of valued fields.

To eliminate quantifiers in the first-order theory of the p-adic field Qp, Ax and Kochen use a language containing a symbol for a cross-section map n → pn from the value group Z into Qp [1, pp. 48–49]. The primitive-recursive quantifier eliminations given by Cohen [2] and Weispfenning [10] also apply to a language mentioning the cross-section, but none of these authors seems entirely happy with his results. As Cohen says, “all the operations… introduced for our simple functions seem natural, with the possible exception of the map n → pn” [2, p. 146]. So all three authors show that various consequences of quantifier elimination—completeness, decidability, model-completeness—also hold for a theory of Qp not employing the cross-section [1, p. 453; 2, p. 146; 10, §4]. Macintyre directs a more specific complaint against the cross-section [5, p. 605]. Elementary formulae which use it can define infinite discrete subsets of Qp; yet infinite discrete subsets of R are not definable in the language of ordered fields, and so certain analogies between Qp and R suggested by previous model-theoretic work seem to break down.

To avoid this problem, Macintyre gives up the cross-section and eliminates quantifiers in a theory of Qp written just in the usual language of fields supplemented by a predicate V for Qp's valuation ring and by predicates Pn for the sets of nth powers in Qp (for all n ≥ 2).

The notion of a higher level ordering is a generalization of the usual notion of an order introduced by Becker in the study of sums of even powers in a field; see [1] for a general reference. A precise definition of an ordering of level 2n (level n in the terminology of [1]) is given in Definition 1.1(II) below.

In [1] Becker worked out the extension theory of fields with a higher level ordering and introduced the notion of a (generalized) real closure for such fields. For a survey of (the analog of) the Artin-Schreier theory of fields with a higher level ordering, see [2]. In [10] Jacob proved decidability, completeness and model-completeness (in a suitable language) for the theory of generalized real-closed fields. Jacob's results are in a sense optimal insofar as the nonuniqueness of generalized real closures (see [1, Chapter IV, Theorems 12 and 13]) prevents quantifier elimination results from holding in languages natural from an algebraic point of view.

The following remarkable fact stems from the work of Becker and Harman: a field having a proper ordering (i.e. one which is not just an order) of any level necessarily has an ordering of (exact) level 2n for each integer n ≥ 2, plus two usual orders, and, moreover, a tight connection holds between orderings of two consecutive levels (cf. [9, Corollary 1.4] and [1, Theorem 15, p. 37]).

In [8], we have shown the equivalence of almost strong minimality and strong unidimensionality. More precisely, we proved:

Theorem [8]. Let T be a countable stable theory. Then the following two conditions are equivalent:

(i) T is almost strongly minimal;

(ii) T can be extended to a theory such that any two nonalgebraic types are not almost orthogonal.

In the present paper, we define the notion of strong 2-dimensionality (of T). We show that if T is strongly 2-dimensional then T is ω-stable and its model has a simple structure. Roughly speaking, in a model of a strongly 2-dimensional theory, one of the following holds: (a) every element is in acl (δi is strongly minimal), or (b) every element is in acl (δ is strongly regular). Shelah's definition of 2-dimensionality does not imply even superstability. (See Exercise 5.5 in [6, Chapter V, §5].) We show also that condition (a) above implies strong 2-dimensionality of T. However condition (b) does not imply strong 2-dimensionality in general.

Our notations and conventions are standard. T is always countable and stable. We work in . A,B,… are used to denote small subsets of . , … are used to denote finite sequences of elements in . δ, φ,… are used to denote formulas (with parameters), p, q, … are used to denote types (with parameters). The fact that p is a nonforking (forking) extension of q is denoted by p ⊃nfq(p ⊃fq). If p is stationary, p∣A denotes the type in S(A) which is parallel to p. (or ) denotes the set of realizations of p (or δ). The Morley rank of p is denoted by RM(p).

We use connections between conjunctive game formulas and the theory of inductive definitions to define the notions of a coinductive formula and its approximations. Corresponding to the theory of conjunctive game formulas we develop a theory of coinductive formulas, including a covering theorem and a normal form theorem for many sorted languages. Applying both theorems and the results on “model interpolation” obtained in this paper, we prove a many-sorted interpolation theorem for ω1ω-logic, which considers interpolation with respect to the language symbols, the quantifiers, the identity, and countably infinite conjunction and disjunction.