In [1] the ω-consistency of arithmetic was proved by a method which yields fine ordinal bounds for κ-consistency, κ ≥ 1. In this paper these bounds are shown to be best possible. The ω-consistency of a number-theoretic system S can be expressed thus: for all sentences ∃xM,
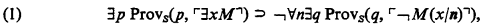
where ProvS is the proof predicate for S, if n is a nonnegative integer then n is the formal numeral (of S) for n, and if G is a formula then ˹G˺ is the Gödel number of G. The κ-consistency of S is the restriction of (1) to Σκ 0 sentences ∃xM. The proof in [1] establishes the no-counterexample interpretation of (1), that is, the existence of a constructive functional Φ such that, for all sentences ∃xM, all numbers p, and all functions f,

(see [1, §2]). A functional Φ is an ω-consistency functional for S if it satisfies (2) for all sentences ∃xM, and a κ-consistency functional for S if it satisfies (2) for all Σκ 0 sentences ∃xM.
The systems considered in [1] are those obtained from classical first-order arithmetic Z, including the schema for definition of primitive recursive (p.r.) functions, by adjoining, for some p.r. well-founded ordering ≺ of the nonnegative integers, the axiom schema
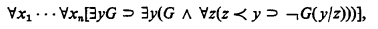
that is, the least number principle on ≺; it is equivalent to the schema of transfinite induction on ≺.