Below are collected some simple results on the theory of free choice sequences [4] or infinitely proceeding sequences (ips) as they are called in [5]. These results are not sufficient to settle the completeness problems for Heyting's predicate calculus [4], as formulated in [12], neither in the strong nor in the weak sense. They are published because they lead to intuitionistically valid versions of completeness proofs which have appeared in the literature, particularly [16], [17], [18], and, with certain reservations, [1].

The problems considered below (except in §8) differ from those of [12] in the following respect: In [12] we were mainly concerned with formulae of Heyting's predicate calculus which were not even classically provable, and showed that the calculus was complete with respect to certain classes of these formulae. The novel feature was that we established this completeness by means of intuitionistically valid methods, in fact methods which can be formalized in Heyting's arithmetic. Here we are primarily concerned with formulae which are classically, but not intuitionistically, provable. As pointed out in [12], the nature of the completeness problem for such formulae is totally different: the class of predicates which provides the required counterexamples must come from a system (with an intuitionistically acceptable interpretation) which, unlike Heyting's arithmetic, is not a subsystem of the corresponding classical system. An example of such a system is an extension FC, given below, of Heyting's formalization of the theory of free choices.

In this paper we answer some of the questions left open in [2]. We use the terminology of [2]. In particular, a theory will be a formal system formulated within the first-order calculus with identity. A theory is identified with the set of Gödel numbers of the theorems of the theory. Thus Craig's theorem [1] asserts that a theory is axiomatizable if and only if it is recursively enumerable.

In [2], Feferman showed that if A is any recursively enumerable set, then there is an axiomatizable theory T having the same degree of unsolvability as A. (This result was proved independently by D. B. Mumford.) We show in Theorem 2 that if A is not recursive, then T may be chosen essentially undecidable. This depends on Theorem 1, which is a result on recursively enumerable sets of some independent interest.

Our second result, given in Theorem 3, gives sufficient conditions for a theory to be creative. These conditions are more general than those given by Feferman. In particular, they show that the system of Kreisel described in [2] is creative.

If a contradiction is deduced by using only the defining formula of a set, it is called a contradiction of Russell's type, and the set is called inconsistent. A set is called consistent, if no contradiction can be deduced from the defining formula of the set.

The object of this note is to determine some conditions for some sets to be consistent or inconsistent.

In §1 notations and terms are defined. In §2 main results are stated. In §3, the proof in UL of a contradiction is simplified for a special kind of sets, so that a simplified definition of the proof of a contradiction is given for the kind of sets, and some properties of a proof in UL are stated concerning the simplified definition. This definition and the properties of a proof are the basis of the proof of the results given in §§5–10. Thus, this Part (V), except §3, is written independently of other Parts as far as possible. However, it depends essentially on Parts (I) and (II). In §4 some examples are given.

In this note we shall prove a certain relative recursiveness lemma concerning countable models of set theory (Lemma 5). From this lemma will follow two results about special types of such models.

Kreisel [5] and Mostowski [6] have shown that certain (finitely axiomatized) systems of set theory, formulated by means of the ϵ relation and certain additional non-logical constants, do not possess recursive models. Their purpose in doing this was to construct consistent sentences without recursive models. As a first corollary of Lemma 5, we obtain a very simple proof, not involving any formal constructions within the system of the notions of truth and satisfiability, of an extension of the Kreisel-Mostowski theorems. Namely, set theory with the single non-logical constant ϵ does not possess any recursively enumerable model. Thus we get, as a side product, an easy example of a consistent sentence containing a single binary relation which does not possess any recursively enumerable model; this sentence being the conjunction of the (finitely many) axioms of set theory.

Mr. L. J. Cohen's interesting example of a logical truth of indirect discourse appears to be capable of a simple formalisation and proof in a variant of first order predicate calculus. His example has the form:

If A says that anything which B says is false, and B says that something which A says is true, then something which A says is false and something which B says is true.

Let ‘A says x’ be formalised by ‘A(x)’ and let assertions of truth and falsehood be formalised as in the following table.

We treat both variables x and predicates A (x) as sentences and add to the familiar axioms and inference rules of predicate logic a rule permitting the inference of A(p) from (x)A(x), where p is a closed sentence.

We have to prove that from

Professor R. L. Goodstein's neat proposal for formalising and proving the Policeman — the logical truth mentioned in my paper — illustrates the main thesis of that paper, viz., that in formalising the logic of indirect discourse one needs to avoid assigning what was said, and the report that it was said, to different levels of a semantical hierarchy. But there are two main difficulties in his proposal:

1. It is not quite clear whether the axioms and rules of Prof. Goodstein's system are to be such that substitutivity of the biconditional is maintained for all wff. If so, the system takes no account of the referentially opaque quality of indirect discourse. For example, the analogue for “If Sir Walter Scott always says the same as the author of Waverley, then George III says that anything Sir Walter Scott says is true if and only if George III says that anything the author of Waverley says is true” would be provable, though this statement is not logically true. If “A(x){Bx→x)” is well-formed (as it must be for Professor Goodstein's proof), the corresponding theorem is

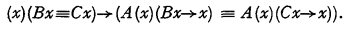
2. In interpreting the letters “A”, “B”, etc. as operators, so that sentences are the substitution-instances both for variables like “x” and for schematic functions of those variables like “Ax”, Professor Goodstein's system does not provide for formalising logical truths in which ordinary predication also plays a part: e.g., “If the policeman says that all women are dangerous drivers and anything the policeman says is true, then no non-dangerous drivers are women”.

On sait que la conjonction et la négation constituent un système de connecteurs suffisant pour formuler le calcul des propositions classiques. Un certain intêrêt s'attache à ces formulations par suite des faits suivants: – les thèses du calcul intuitioniste qui ne comprennent pas d'autres connecteurs que la conjonction et la négation sont identiques aux thèses classiques;

– Lewis ayant formulé ses calculs modaux en prenant la conjonction, la négation et la possibilité comme connecteurs primitifs (voir Lewis-Langford 1932, ch. VI) et ayant été suivi par beaucoup de chercheurs s'occupant de modalités, le calcul classique fondé sur la conjonction et la négation est contenu dans la plupart des systèmes modaux que l'on trouve dans la littérature.

Un système logistique pour le calcul classique fondé sur la conjonction et la négation a été étudié par Rosser (voir Rosser 1953, ch. 4; aussi Copi 1954, ch. 7).

Dans cet article je vais définir cinq autres systèmes logistiques fondés sur les mêmes connecteurs, démontrer leur suffisance (en utilisant les résultats publiés de Rosser et de Copi), et — sauf un cas — démontrer l'indépendance des axiomes de chacun de ces systèmes.