It has been pointed out by Carnap that ‘probability’ is an equivocal term, which is used currently in two senses: (i) the degree to which it is rational to believe a hypothesis h on specified evidence e, and (ii) the relative frequency (in an indefinitely long run) of one property of events or things with respect to another. This paper is concerned only with the first of these two senses, which will be referred to as ‘the concept of confirmation,’ in order to avoid equivocation.

We may distinguish a quantitative and a comparative concept of confirmation. The general form of statements involving the former is

The degree of confirmation of the proposition h, given the proposition

e as evidence, is r (where r is a real number between 0 and 1).

In this paper the notation for a statement of this form is

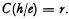
The general form of statements involving the comparative concept is The proposition h is equally or less confirmed on e than is the proposition h′ on e′,

which may be symbolized as

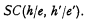
The following abbreviations will also be used in discussing comparative confirmation:

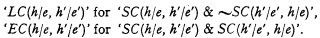
The former of these two abbreviations means intuitively

The proposition h is less confirmed on evidence e than h′ is on e′. The latter means

The proposition h is confirmed on evidence e to the same degree that h′ is on e′.

We prove the following theorem: If S is a consistent set of axioms for set theory, among whose consequences are the axioms of pairing and extensionality, and if S′ is the extension of S to all classes of sets of S, then S′ is consistent and remains so upon addition of an axiom expressing that the universal class has a well-ordering wherein every non-initial element has an immediate predecessor.

The basic idea will be use of the denumerable model of S guaranteed by the Skolem-Löwenheim theorem to obtain (i) a model of S′ in the domain of classes of natural numbers, and (ii) a correspondence between representatives (in the model of S′) of sets of S′ and natural numbers. One can then select a class of natural numbers in the model of S′ which will well-order (in the sense of the model of S′) the representatives of sets of S′ according to the numbers corresponding to them.

Specifically, let the formulas of S involve only one kind of variable and the sole predicate ‘ϵ’. The formulas of S′ can be thought of as identical with those of S; but the axioms of S′ will consist of (i) those of S with quantifiers restricted to sets by clauses ‘(∃z)[y ϵ z]’, (ii) those provided by the schema ‘(∃x) ▪ y ϵ x ≡y [(∃z)[y ϵ z] ▪ A]’, where ‘A’ is any formula of S′ in which ‘x is not free, and (iii) the axiom of extensionality.

In applying the method of arithmetization to a proof of the completeness of the predicate calculus, Bernays has obtained a result which, when applied to set theories formulated in the predicate calculus, may be stated thus.

1.1. By adding an arithmetic sentence Con(S) (expressing the consistency of a set theory S) as a new axiom to the elementary number theory Zμ (HB II, p. 293), we can prove in the resulting system arithmetic translations of all theorems of S.

It then follows that things definable or expressible in S have images in a simple extension of Zμ, if S is consistent. Since S can be a “strong” system, this fact has interesting consequences. Some of these are discussed by me and some are discussed by Kreisel. Kreisel finds an undecidable sentence of set theory by combining 1.1 and the Cantor diagonal argument. I shall prove below, using similar methods, a few further results, concerned with the notions of truth and designation. The method of numbering sets which I use (see 3.1 below) is different from Kreisel's. While the method used here is formally more elegant, Kreisel's method is much more efficient if we wish actually to calculate the numerical values.