It is well-known that every involution in a logical or mathematical system gives rise to a theory of duality; for example, negation in the sentential calculus and predicate calculus, complementation in the calculus of classes, complementation and conversion in the calculus of relations, etc. The purpose of this note is to call attention to the fact that every involution in a logical or mathematical system gives rise to a theory of quaternality and that the square of quaternality, of which the classical squares of opposition are special cases, provides a diagrammatic representation for much of the theory of quaternality. For the sake of definiteness we expose the theory of quaternality in the context of the lower predicate calculus.

Let ϕ and ψ be formulas of the lower predicate calculus. The constants {T and F} {∧ and ∨} {→ and ⇷} {← and ⇸}{↔ and ⇹} {↑ and ↓} {∧ (all) and ∨ (some)} are dual. The constant ~ is self-dual. The negational of ϕ, denoted ϕN, is the formula obtained from ϕ by interchanging negated and unnegated variables (that is, sentence variables and predicate variables) and by interchanging dual constants. The contradual of ϕ, denoted ϕC, is the formula obtained from ϕ by interchanging negated and unnegated variables. The dual of ϕ, denoted ϕD, is the formula obtained from ϕ by interchanging dual constants. The four formulas ϕ, ϕN, ϕC, ϕD, are quaternals of each other.

In a recent paper by Mostowski [1] we find an investigation of those formulas of quantification theory which are valid in all domains of individuals, including the empty domain. Mostowski gives a complete set of axioms for such a first order functional calculus (the system is called “”) and a comparison is made with a form of the usual calculus, Church's in [2]. It is pointed out that is much less elegant; in particular, the distributivity laws for quantifiers (e.g., (x){A . B) .{x)A . (x)B) do not hold in general, and likewise the rule of modus ponens does not preserve validity in all cases.

In this paper we show that a not inelegant system is obtained if one modifies Mostowski's approach in two respects; and once this is done a somewhat neater proof of completeness can be given.

The first respect in which we diverge from Mostowski is in the treatment of vacuous quantifiers. For him if p has no free x, then (x)p and (∃x)p are both to have the same value (interpretation) as p1. But this is not the only way to assign values to vacuous quantifications. For when universal quantification is viewed as a generalized conjunction, the formula (x)Fx has the significance of Fa . Fb…. for as many conjunctands as there are individuals in the domain, and if Fx should have the “constant” value p, then (x)p is to mean the conjunction of p with itself for as many times as there are individuals in the domain (compare the arithmetical ).

Let and be (well-formed) formulas of the functional calculus, let c be an n-adic functional variable, and let a1, …, an be distinct individual variables. Church has defined the metalogical notation to indicate the formula resulting from when each part of of the form c{1, …, n) (such that the occurrence of c is free in ) is replaced by the formula which arises from by replacing every free occurrence of ai by i, i, = 1, …, n. (Here 1, …, n may be any individual variables or constants, not necessarily all distinct.) The notation is not defined for all , , c, a1, …, an, however, but only for those cases (specified in detail by Church) when the resulting formula constitutes a valid substitution instance of the formula according to the standard interpretation of the functional calculus.

The full and correct syntactical statement of the conditions (under which this type of substitution is permissible) has proved so arduous, that it seems to have been rendered in error more often than not. Unfortunately the functional calculi are often set up as deductive systems in which this type of substitution occurs as one of the primitive rules of inference, or in one of the axiom schemata. Thus the beginning student who is introduced to the calculi through such a formulation is forced to cope from the outset with details which have proved treacherous even to the initiate. For this reason it is desirable to seek alternative formulations of the functional calculi in which this type of substitution is not mentioned.

The problem of constructing formal systems involving transfinite types was briefly suggested many times in the literature. Actually few attempts have been made to develop such systems. In particular, there exists a system based on a set of axioms and rules of inference suggested by Church and worked out in detail by E. Bustamante in his dissertation. Recently, John Kemeny has reformulated this system in a simplified way and has obtained an interesting hierarchy of systems. It so happens that all these systems considered by Kemeny may be regarded as successive extensions of a particular formulation of the theory of finite types, namely a certain monadic functional calculus of order ω whose main ideas are due to Tarski.

There exists on the other hand a quite different formulation of the theory of finite types which is due to Church. It is a formulation which incorporates certain features of the calculus of λ-conversion, and which has revealed itself quite advantageous for certain purposes. The formulation of the theory of transfinite types which we are going to introduce in this paper may be considered as an attempt to generalize Church's formulation of the theory of finite types.

In a recent paper [4] on mean value theorems in recursive function theory we proved the theorem that

(A) iff(n, x) is relatively differentiable with a relative derivative f1(n, x), for a ≤ x ≤ b, and if f(n, a) = f(n, b) = 0 relative to n,

then there is a recursive function ck, a < ck < b, and a recursive R(k) such that f1(n, ck) = 0(k) for n ≥ R(k); and we showed further that the added condition

(B) f(n, x) is either relatively variable or relatively constant

suffices to ensure that ck is uniformly contained in (a, b), i.e. that there exist α, β such that

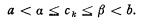
A comparison with the conditions under which Rolle's theorem is established in classical analysis suggests that clause (A) itself might suffice to ensure that ck is uniformly contained in (a, b); for in the classical theory there is a single point c, a < c < b, for which lim f1(n, c) = 0, and therefore f1(n, c) = 0(k) for sufficiently great values of n, where of course c is independent of k.

The object of the present note is to show that this is not in fact the case, and we shall construct a recursive function f(n, x) satisfying condition (A) in the interval (0, 1) and such that any sequence ck for which f1(n, ck) = 0(k) for large enough values of n is not uniformly contained in (0, 1).

The usual logical paradoxes, which stem from Russell's class R0 (i.e., and its relatives R1, R2, and so on (i.e., , , and so on, correspondingly), are contradictions (Ri ϵ Ri) ≡ ~(Ri ϵ Ri), derivable under unrestricted rules of inference. No contradiction appears to obtain.

Lewis and Langford state, “… it appears that the relation of strict implication expresses precisely that relation which holds when valid deduction is possible. It fails to hold when valid deduction is not possible. In that sense, the system of strict implication may be said to provide that canon and critique of deductive inference which is the desideratum of logical investigation.” Neglecting for the present other possible criticisms of this assertion, it is plausible to maintain that if strict implication is intended to systematize the familiar concept of deducibility or entailment, then some form of the deduction theorem should hold for it. The purpose of this paper is to analyze and extend some results previously established which bear on the problem.

We will begin with a rough statement of some relevent considerations. Let the system S contain among its connectives an implication connective ‘I’ and a conjunction connective ‘&’. Let A1, A2, …, An ⊦ B abbreviate that B is provable on the hypotheses A1, A2, …, An for a suitable definition of “proof on hypotheses”, where A1, A2, …, An, B are well-formed expressions of S.

The 2-valued calculus of non-contradiction of Dexter has been extended to 3-valued logic. The methods used were, however, too complicated to be capable of generalisation to m-valued logics. The object of the present paper is to give an alternative method of generalising Dexter's work to m-valued logics with one designated truth-value. The rule of procedure is generalised in the same way as before, but the deductive completeness of the system is proved by applying results of Rosser and Turquette. The system has an infinite set of primitive functions, written n(P1, P2, …, Pr) (r = 1,2, …). With the notation of Post, n(P1, P2, …, Pr) has the same truth-value as ~(P1 & P2 & … & Pr). Thus n(P) is Post's primitive ~P, and we can define & by

We use n2(P1, P2, …, Pr) as an abbreviation for n(n(P1, P2, …, Pr)); similarly for higher powers of n. But if we set up the 1-1 correspondence of truth-values i ↔ m−i+1, then & corresponds to ∨ and ~m−1 corresponds to ~. Hence the functional completeness of our system follows from a theorem of Post.

We define the functions N(P), N(P, Q) by

Thus the truth-value of N(P) is undesignated if and only if the truth-value of P is designated, and the truth-value of N(P, Q) is undesignated if and only if the truth-values of P and Q are both designated.

During the past several decades, linguists have developed and applied widely techniques which enable them, to a considerable extent, to determine and state the structure of natural languages without semantic reference. It is of interest to inquire seriously into the formality of linguistic method and the adequacy of whatever part of it can be made purely formal, and to examine the possibilities of applying it, as has occasionally been suggested, to a wider range of problems. In order to pursue these aims it is first necessary to reconstruct carefully the set of procedures by which the linguist derives the statements of a linguistic grammar from the behaviour of language users, distinguishing clearly between formal and experimental in such a way that grammatical notions, appearing as definienda in a constructional system, will be formally derivable for any language from a fixed sample of linguistic material upon which the primitives of the system are experimentally defined. The present paper will be an attempt to formalize a certain part of the linguist's generalized syntax language.

From another point of view, this paper is an attempt to develop an adequate notion of syntactic category within an inscriptional nominalistic framework. The inscriptional approach seems natural for linguistics, particularly in view of the fact that an adequate extension of the results of this paper will have to deal with the problem of homonymity, i.e., with a statement of the conditions under which tokens of the same type must be assigned to different syntactic classes.