The purpose of this paper is to put on record some theorems relating to improvements in the primitive frame of combinatory logic. These improvements were, for the most part, suggested by the work of Rosser, who formulated a weakened system of combinatory logic in which the rules had a simple character not possessed by those of the original system. In the latter the rules B, C, W, K were in reality axiom-schemes, and their postulation amounted to assuming infinitely many axioms. Rosser had rules of procedure such that no propositions were deducible from them except in combination with axioms (or previously proved propositions); moreover, the conclusion of each rule was uniquely determined by the premises. He also eliminated equality as a primitive term, defining it (essentially) according to the traditional method. This paper shows that these and related advantages apply to certain formulations of the full system of combinatory logic, so far as it concerns the theory of combinators.

The method of procedure is as follows. Instead of setting up a primitive frame at the start and then deriving its properties, I begin (after some preliminary explanations in §2) by stating in §3 the properties which it is desired to establish. The next few sections are devoted to the formulation and proof of certain general theorems concerning possible bases for the system of §3. These theorems are, perhaps, more general than is necessary for the immediate purpose, but they are of some interest on their own account. A formulation in terms of the primitives of original system (i.e., B, C, W, and K), which is of the same general type as Rosser's formulation, is obtained at the end of §6. In §7 are discussed the changes in this formulation which are sufficient in order to base it on the primitive combinators S and K of Schönfinkel.

The consistency of the theory of combinators, when based on the combinatory axioms, the rules of equality, and the equations

was proved in my thesis; likewise some theorems expressing certain completeness properties of this theory of combinatory equivalence formed the principal subject of that thesis and a succeeding paper. Further theorems of this sort were later demonstrated by Rosser; his theorems are, in some cases, more powerful than those just mentioned, but they apply to a weakened system. The purpose of this note is to discuss the extension of these theorems to the case where the whole of the theory of combinators is taken into account, and the rules for equality are derived from more fundamental considerations.

The paper is based on a formulation of the theory of combinators contained in a previous paper, acquaintance with which is presupposed.

A key theorem in investigations of this character is a theorem proved in 1936 by Church and Rosser. It is necessary to give a brief account of this theorem together with a generalization of it.

The theorem concerns a certain formalism, which I shall here call the λ-formalism. The terms of this formalism, which I shall call λ-terms, are constituted as follows. For primitive terms we have an infinite set of variables, together with certain constants, the nature of which is arbitrary. Further terms are formed by two operations: a binary operation (analogous to application in the theory of combinators) which combines two λ-terms 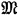and 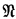to form a new λ-term here symbolized by 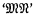; and another binary operation combining a variable x and a term 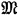containing x as free variable to form a term .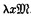