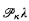We introduce the notion of skinniness for subsets of 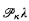 and its variants, namely skinnier and skinniest. We show that under some cardinal arithmetical assumptions, precipitousness or 2λ-saturation of NSκλ ∣ X, where NSκλ denotes the non-stationary ideal over
and its variants, namely skinnier and skinniest. We show that under some cardinal arithmetical assumptions, precipitousness or 2λ-saturation of NSκλ ∣ X, where NSκλ denotes the non-stationary ideal over 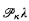 , implies the existence of a skinny stationary subset of X. We also show that if λ is a singular cardinal, then there is no skinnier stationary subset of
, implies the existence of a skinny stationary subset of X. We also show that if λ is a singular cardinal, then there is no skinnier stationary subset of 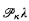 . Furthermore, if λ is a strong limit singular cardinal, there is no skinny stationary subset of
. Furthermore, if λ is a strong limit singular cardinal, there is no skinny stationary subset of 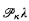 . Combining these results, we show that if λ is a strong limit singular cardinal, then NSκλ ∣ X can satisfy neither precipitousness nor 2λ-saturation for every stationary X ⊆
. Combining these results, we show that if λ is a strong limit singular cardinal, then NSκλ ∣ X can satisfy neither precipitousness nor 2λ-saturation for every stationary X ⊆ 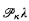 . We also indicate that
. We also indicate that 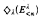 , where
, where 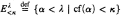 , is equivalent to the existence of a skinnier (or skinniest) stationary subset of
, is equivalent to the existence of a skinnier (or skinniest) stationary subset of 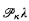 under some cardinal arithmetical hypotheses.
under some cardinal arithmetical hypotheses.