Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T17:34:43.652Z Has data issue: false hasContentIssue false
  • English
  • Français

An indeterminate in number theory

Part of: Elementary number theory

Published online by Cambridge University Press:  09 April 2009

Emma Lehmer
Emma Lehmer
Affiliation:
1180 Miller Avenue Berkeley, California 94708, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper studies quintic residuacity of primes p of the form 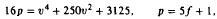for which the expression for 4f modulo p given in the first volume of this journal becomes indeterminate, and replaces it by a much simpler expression.

MSC classification

Secondary: 11A15: Power residues, reciprocity
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 46 , Issue 3 , June 1989 , pp. 469 - 472
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Katre, S. A. and Rajwade, A. J., ‘Euler criterion for quintic non-residues,’ Canad. J. Math. 37 (1985), 1008–1024.CrossRefGoogle Scholar
[2]Lehmer, Emma, ‘On Euler's criterion,’ J. Austral. Math. Soc. 1 (1959), 64–70.Google Scholar
[3]Lehmer, Emma, ‘Artiads characterized,’ J. Math. Anal. Appl. 15 (1966), 118–131.CrossRefGoogle Scholar
[4]Lehmer, Emma, ‘On the divisors of the discriminant of the period equation,’ Amer. J. Math. 90 (1968), 375–379.CrossRefGoogle Scholar
[5]Tanner, H. W., ‘On the binomial equation xp – 1: Quintesection,’ Proc. London Math. Soc. 18 (1866–1867), 214–234.Google Scholar
[6]Williams, Kenneth S., ‘On Euler's criterion for quintic nonresidues,’ Pacific J. Math. 61 (1975), 543–550.CrossRefGoogle Scholar