Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Morrow, Steven T.
2018.
A moment coboundary theorem for C[0,1]-valued random fields.
Statistics & Probability Letters,
Vol. 142,
Issue. ,
p.
62.
Morrow, Steven T.
2021.
An $$L^p$$ Multiplicative Coboundary Theorem for Sequences of Unitriangular Random Matrices.
Journal of Theoretical Probability,
Vol. 34,
Issue. 1,
p.
206.

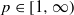 and a given strictly stationary sequence of random variables, the
and a given strictly stationary sequence of random variables, the 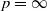 is included.
is included.