Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Walker, Peter
1996.
Upper bounds for the separation of real zeros of polynomials.
Proceedings of the Edinburgh Mathematical Society,
Vol. 39,
Issue. 2,
p.
357.
Anderson, Bruce B.
1997.
Where the Inflection Points of a Polynomial May Lie.
Mathematics Magazine,
Vol. 70,
Issue. 1,
p.
32.
Walker, Peter
1997.
Separation of Zeros of Translates of Polynomials and Entire Functions.
Journal of Mathematical Analysis and Applications,
Vol. 206,
Issue. 1,
p.
270.
Walker, Peter
2002.
The zeros of linear combinations of translates of polynomials.
Journal of the Australian Mathematical Society,
Vol. 72,
Issue. 1,
p.
109.
Boelkins, Matthew
From, Justin
and
Kolins, Samuel
2008.
Polynomial Root Squeezing.
Mathematics Magazine,
Vol. 81,
Issue. 1,
p.
39.
Brändén, Petter
Krasikov, Ilia
and
Shapiro, Boris
2016.
Elements of Pólya-Schur theory in the finite difference setting.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 11,
p.
4831.
Kiselev, Alexander
and
Tan, Changhui
2022.
The Flow of Polynomial Roots Under Differentiation.
Annals of PDE,
Vol. 8,
Issue. 2,


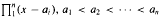 by δ(
by δ(