Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dubtsov, E. S.
2007.
Characterizations of Hardy-Orlicz and Bergman-Orlicz spaces.
Journal of Mathematical Sciences,
Vol. 141,
Issue. 5,
p.
1531.

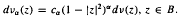 Here
Here 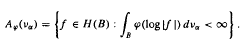
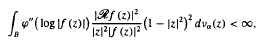 where
where 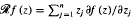 is the radial derivative of
is the radial derivative of 