Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T17:30:58.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractional powers of generators of equicontinuous semigroups and fractional derivatives

Part of: General theory of linear operators

Published online by Cambridge University Press:  09 April 2009

Oscar E. Lanford III  and
Derek W. Robinson
Oscar E. Lanford III
Affiliation:
IHES 91440 Bures-sur-Yvette, France
Derek W. Robinson
Affiliation:
Mathematics Department, Institute of Advanced Studies, Australian National University, Canberra, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We analyze fractional powers Hα, α > 0, of the generators H of uniformly bounded locally equicontinuous semigroups S. The Hα are defined as the αth derivative δα of the Dirac measure δ evaluated on S. We demonstrate that the Hα are closed operators with the natural properties of fractional powers, for example, HαHβ = Hα+β for α, β > 0, and (Hα)β = Hαβ for 1 > α > 0 and β > 0. We establish that Hα can be evaluated by the Balakrishnan-Lions-Peetre algorithm 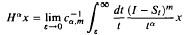where m is an integer larger than α, Cα, m is a suitable constant, and the limit exists in the appropriate topology if, and only if, x ∈ D(Hα). Finally we prove that H∈ is the fractional derivation of S in the sense 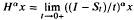where the limit again exists if, and only if, x ∈ D(Hα).

MSC classification

Secondary: 47A99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 46 , Issue 3 , June 1989 , pp. 473 - 504
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Arveson, W., ‘On groups of automorphisms of operator algebras’, J. Funct. Anal. 15 (1974), 217–243.CrossRefGoogle Scholar
[2]Balakrishnan, A. V., ‘An operational calculus for infinitesimal generators of semigroups’, Trans. Amer. Math. Soc. 91 (1959). 330–353.Google Scholar
Balakrishnan, A. V., ‘Fractional powers of closed operators and the semigroups generated by them’, Pacific J. Math. 10 (1960), 419–437.CrossRefGoogle Scholar
[3]Berens, H., Butzer, P. L., and Westphal, U., ‘Representation of fractional powers of infinitesimal generators of semigroups’, Bull. Amer. Math. Soc. 74 (1968), 191–196.CrossRefGoogle Scholar
[4]Berg, C. and Forst, G., Potential theory on locally compact abelian groups (Springer-Verlag, 1975).CrossRefGoogle Scholar
[5]Bochner, S., ‘Diffusion equations and stochastic processes’, Proc. Nat. Acad. Sci. U.S.A. 35 (1949), 369–370.CrossRefGoogle ScholarPubMed
[6]Bratteli, O. and Robinson, D. W., Operator algebras and quantum statistical mechanics. I (Springer-Verlag, 1979).CrossRefGoogle Scholar
[7]de Leeuw, K., ‘On the adjoint semigroup and some problems in the theory of approximation’, Math. Z. 73 (1960), 219–234.CrossRefGoogle Scholar
[8]Dunford, N. and Schwartz, J. T., Linear operators. I (Interscience, 1958).Google Scholar
[9]Friedman, A., Partial differential equations (Holt, Reinhart and Winston, New York, 1969).Google Scholar
[10]Kato, T., ‘Note on fractional powers of linear operators’, Proc. Japan Acad. 36 (1960), 94–96.Google Scholar
[10]Kato, T., ‘Fractional powers of dissipative operators’, J. Math. Soc. Japan 13 (1961), 246–274.CrossRefGoogle Scholar
[11]Komatsu, H., ‘Fractional powers of operators’, Pacific J. Math. 19 (1966), 285–346.CrossRefGoogle Scholar
Komatsu, H., ‘Fractional powers of operators. II. Interpolation spaces’, Pacific J. Math. 21 (1967), 89–111.CrossRefGoogle Scholar
Komatsu, H., ‘Fractional powers of operators. III. Negative powers’, J. Math. Soc. Japan 21 (1969), 205–220.CrossRefGoogle Scholar
Komatsu, H., ‘Fractional powers of operators. IV. Potential operators’, J. Math. Soc. Japan 21 (1969), 221–228.CrossRefGoogle Scholar
Komatsu, H., ‘Fractional powers of operators. V. Dual Operators’, J. Fac. Sci. Univ. Tokyo 17 (1970), 373–396.Google Scholar
[12]Krasnoselskii, M. A. and Sobolevskii, P. E., ‘Fractional powers of operators defined on Banach space’, Dokl. Akad. Nauk SSSR 129 (1959), 499–502.Google Scholar
[13]Krasnoselskii, M. A., Zabreiko, P. D., Pustylnik, E. I., and Sobolevskii, P. E., Integral operators in spaces of summable functions (Noordhoff, Leiden, 1976).CrossRefGoogle Scholar
[14]Lions, J. L. and Peetre, J., ‘Sur une classe d'espaces d'interpolation’, Inst. Hautes Études Sci. Publ. Math. 19 (1964), 5–68.CrossRefGoogle Scholar
[15]Nelson, E., ‘A functional calculus using singular Laplace integrals’, Trans. Amer. Math. Soc. 88 (1958), 400–413.CrossRefGoogle Scholar
[16]Pazy, A., Semigroups of linear operators and applications to partial differential equations (Springer-Verlag, 1983).CrossRefGoogle Scholar
[17]Phillips, R. S., ‘On the generation of semi-groups of linear operators’, Pacific J. Math. 2 (1952), 343–369.CrossRefGoogle Scholar
[18]Schwartz, L., Lectures on mixed problems in partial differential equations and the representation of semigroups (Tata Inst. of Fund. Res., Bombay, 1958).Google Scholar
[19]Tanabe, H., Equations of evolution (Pitman, London, 1979).Google Scholar
[20]Triebel, H., Interpolation theory, function spaces, differential operators (North-Holland, 1978).Google Scholar
[21]Watanabe, J., ‘On some properties of fractional powers of linear operators, Proc. Japan Acad. 37 (1961), 273–275.Google Scholar
[22]Yosida, K., Functional anaĺysis (Springer-Verlag, 1974).CrossRefGoogle Scholar