Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T15:23:16.274Z Has data issue: false hasContentIssue false
  • English
  • Français

LIMITS OF FRACTIONAL DERIVATIVES AND COMPOSITIONS OF ANALYTIC FUNCTIONS

Part of: Series expansions Miscellaneous topics of analysis in the complex domain

Published online by Cambridge University Press:  28 September 2016

THOMAS H. MACGREGOR  and
MICHAEL P. STERNER
THOMAS H. MACGREGOR
Affiliation:
Bowdoin College, Brunswick, ME 04558, USA email t@thomasmacgregor.com
MICHAEL P. STERNER*
Affiliation:
University of Montevallo, Montevallo, AL 35115, USA email sternerm@montevallo.edu
*
✉sternerm@montevallo.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that the function 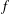$f$ is analytic in the open unit disk 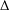$\unicode[STIX]{x1D6E5}$ in the complex plane. For each 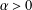$\unicode[STIX]{x1D6FC}>0$ a function 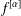$f^{[\unicode[STIX]{x1D6FC}]}$ is defined as the Hadamard product of 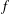$f$ with a certain power function. The function 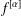$f^{[\unicode[STIX]{x1D6FC}]}$ compares with the fractional derivative of 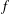$f$ of order $\unicode[STIX]{x1D6FC}$. Suppose that 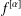$f^{[\unicode[STIX]{x1D6FC}]}$ has a limit at some point 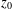$z_{0}$ on the boundary of 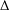$\unicode[STIX]{x1D6E5}$. Then 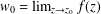$w_{0}=\lim _{z\rightarrow z_{0}}f(z)$ exists. Suppose that 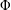$\unicode[STIX]{x1D6F7}$ is analytic in 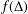$f(\unicode[STIX]{x1D6E5})$ and at 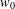$w_{0}$. We show that if 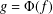$g=\unicode[STIX]{x1D6F7}(f)$ then 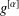$g^{[\unicode[STIX]{x1D6FC}]}$ has a limit at 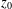$z_{0}$.

Keywords

analytic functionsboundary limitscompositionsfractional derivatives

MSC classification

Primary: 30B99: None of the above, but in this section
Secondary: 30E99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 1 , August 2017 , pp. 104 - 115
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Carathéodory, C., Theory of Functions of a Complex Variable, Vol. 2 (Chelsea, New York, 1954).Google Scholar
Hardy, G. H. and Littlewood, J. E., ‘Some properties of fractional integrals II’, Math. Z. 34 (1932), 403–489.Google Scholar
Kraus, D., Roth, O. and Ruscheweyh, St., ‘A boundary version of Ahlfors’ lemma, locally complete conformal metrics and conformally invariant reflection principles for analytic maps’, J. Anal. Math. 101 (2007), 219–256.CrossRefGoogle Scholar
MacGregor, T. H. and Sterner, M. P., ‘Hadamard products with power functions and multipliers of Hardy spaces’, J. Math. Anal. Appl. 282 (2003), 163–176.Google Scholar
Miller, K. S. and Ross, B., An Introduction to the Fractional Calculus and Fractional Differential Equations (John Wiley & Sons, New York, 1993).Google Scholar
Oldham, K. B. and Spanier, J., The Fractional Calculus (Academic Press, New York, 1974).Google Scholar
Shapiro, J. H., Composition Operators and Classical Function Theory (Springer, New York, 1993).CrossRefGoogle Scholar