Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T19:33:07.442Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone functions mapping the set of rational numbers on itself

Published online by Cambridge University Press:  09 April 2009

B. H. Neumann  and
R. Rado
B. H. Neumann
Affiliation:
The Australian National University
R. Rado
Affiliation:
The University, Reading
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The functions f defined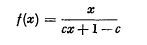 by or by 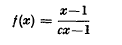for c rational and less than + 1 map the set of rational numbers between 0 and 1 one-to-one onto itself; and they are the only fractional linear functions with this property. Miss Tekla Taylor recently raised the question * whether these are the only differentiable functions with the stated property. In the present note we show, by two different constructions, that the answer is negative; in each case much freedom remains, which could be used to make the functions in question have various additional properties.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 3 , Issue 3 , August 1963 , pp. 282 - 287
Copyright
Copyright © Australian Mathematical Society 1963

References

* Oral communication. A related but simpler problem, proposed by D. G. Northcott and communicated to us by I. D. Macdonald, is solved in a note by Neumann, Peter M. in INVARIANT [the journal of the Oxford University Invariant Society] 1, 9–11 (1961). Subsequently one of us jointly with H. A. Heilbronn obtained a more general result (not published).Google Scholar