Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-13T03:34:09.043Z Has data issue: false hasContentIssue false
  • English
  • Français

NEW COMPLEX ANALYTIC METHODS IN THE THEORY OF MINIMAL SURFACES: A SURVEY

Part of: Classical differential geometry

Published online by Cambridge University Press:  23 August 2018

ANTONIO ALARCÓN  and
FRANC FORSTNERIČ
ANTONIO ALARCÓN
Affiliation:
Departamento de Geometría y Topología e Instituto de Matemáticas (IEMath-GR), Universidad de Granada, Campus de Fuentenueva s/n, E–18071 Granada, Spain email alarcon@ugr.es
FRANC FORSTNERIČ*
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, and Institute of Mathematics, Physics and Mechanics, Jadranska 19, SI–1000 Ljubljana, Slovenia email franc.forstneric@fmf.uni-lj.si
*
✉franc.forstneric@fmf.uni-lj.si
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we survey recent developments in the classical theory of minimal surfaces in Euclidean spaces which have been obtained as applications of both classical and modern complex analytic methods; in particular, Oka theory, period dominating holomorphic sprays, gluing methods for holomorphic maps, and the Riemann–Hilbert boundary value problem. Emphasis is on results pertaining to the global theory of minimal surfaces, in particular, the Calabi–Yau problem, constructions of properly immersed and embedded minimal surfaces in 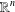$\mathbb{R}^{n}$ and in minimally convex domains of 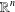$\mathbb{R}^{n}$, results on the complex Gauss map, isotopies of conformal minimal immersions, and the analysis of the homotopy type of the space of all conformal minimal immersions from a given open Riemann surface.

Keywords

minimal surfaceRiemann surfaceOka manifold

MSC classification

Primary: 53A10: Minimal surfaces, surfaces with prescribed mean curvature
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 3 , June 2019 , pp. 287 - 341
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

Antonio Alarcón is partially supported by the grants MTM2014-52368-P and MTM2017-89677-P from MINECO/FEDER, Spain. Franc Forstnerič is partially supported by the research program P1-0291 and the grant J1-7256 from ARRS, Republic of Slovenia.

References

Abraham, R., ‘Transversality in manifolds of mappings’, Bull. Amer. Math. Soc. 69 (1963), 470–474.Google Scholar
Ahlfors, L. V., ‘The theory of meromorphic curves’, Acta Soc. Sci. Fenn. Nova Ser. A 31(4) 1941.Google Scholar
Ahlfors, L. V., Lectures on Quasiconformal Mappings, 2nd edn, University Lecture Series, 38 (American Mathematical Society, Providence, RI, 2006). With supplemental chapters by C. J. Earle, I. Kra, M. Shishikura and J. H. Hubbard.Google Scholar
Alarcón, A., ‘Complete complex hypersurfaces in the ball come in foliations’. Preprint, 2018, arXiv:1802.02004.Google Scholar
Alarcón, A. and Castro-Infantes, I., ‘Interpolation by conformal minimal surfaces and directed holomorphic curves’. Preprint, 2017, arXiv:1701.04379.Google Scholar
Alarcón, A. and Castro-Infantes, I., ‘Complete minimal surfaces densely lying in arbitrary domains of ℝ n ’, Geom. Topol. 22(1) (2018), 571–590.Google Scholar
Alarcón, A., Drinovec Drnovšek, B., Forstnerič, F. and López, F. J., ‘Every bordered Riemann surface is a complete conformal minimal surface bounded by Jordan curves’, Proc. Lond. Math. Soc. (3) 111(4) (2015), 851–886.Google Scholar
Alarcón, A., Drinovec Drnovšek, B., Forstnerič, F. and López, F. J., ‘Minimal surfaces in minimally convex domains’, Trans. Amer. Math. Soc. (to appear) arXiv:1702.08032, doi:10.1090/tran/7331.Google Scholar
Alarcón, A. and Fernández, I., ‘Complete minimal surfaces in ℝ3 with a prescribed coordinate function’, Differential Geom. Appl. 29(suppl. 1) (2011), S9–S15.Google Scholar
Alarcón, A., Fernández, I. and López, F. J., ‘Complete minimal surfaces and harmonic functions’, Comment. Math. Helv. 87(4) (2012), 891–904.Google Scholar
Alarcón, A., Fernández, I. and López, F. J., ‘Harmonic mappings and conformal minimal immersions of Riemann surfaces into ℝN ’, Calc. Var. Partial Differential Equations 47(1–2) (2013), 227–242.Google Scholar
Alarcón, A. and Forstnerič, F., ‘Every bordered Riemann surface is a complete proper curve in a ball’, Math. Ann. 357(3) (2013), 1049–1070.Google Scholar
Alarcón, A. and Forstnerič, F., ‘Every conformal minimal surface in ℝ3 is isotopic to the real part of a holomorphic null curve’, J. reine angew. Math. (to appear), doi:10.1515/crelle-2015-0069.Google Scholar
Alarcón, A. and Forstnerič, F., ‘Null curves and directed immersions of open Riemann surfaces’, Invent. Math. 196(3) (2014), 733–771.Google Scholar
Alarcón, A. and Forstnerič, F., ‘The Calabi–Yau problem, null curves, and Bryant surfaces’, Math. Ann. 363(3–4) (2015), 913–951.Google Scholar
Alarcón, A. and Forstnerič, F., ‘Null holomorphic curves in ℂ3 and applications to the conformal Calabi–Yau problem’, in: Complex Geometry and Dynamics, Abel Symposia, 10 (Springer, Cham, 2015), 101–121.Google Scholar
Alarcón, A. and Forstnerič, F., ‘Darboux charts around holomorphic Legendrian curves and applications’, Int. Math. Res. Not. IMRN (to appear), doi:10.1093/imrn/rnx158.Google Scholar
Alarcón, A., Forstnerič, F. and López, F. J., ‘Every meromorphic function is the Gauss map of a conformal minimal surface’, J. Geom. Anal. (to appear), doi:10.1007/s12220-017-9948-3.Google Scholar
Alarcón, A., Forstnerič, F. and López, F. J., ‘Embedded minimal surfaces in ℝ n ’, Math. Z. 283(1–2) (2016), 1–24.Google Scholar
Alarcón, A., Forstnerič, F. and López, F. J., ‘New complex analytic methods in the study of non-orientable minimal surfaces in ℝ n ’, Mem. Amer. Math. Soc. (to appear) arXiv:1603.01691.Google Scholar
Alarcón, A., Forstnerič, F. and López, F. J., ‘Holomorphic Legendrian curves’, Compos. Math. 153(9) (2017), 1945–1986.Google Scholar
Alarcón, A. and Lárusson, F., ‘Representing de Rham cohomology classes on an open Riemann surface by holomorphic forms’, Internat. J. Math. 28(9) (2017), 1740004,12.Google Scholar
Alarcón, A. and López, F. J., ‘Minimal surfaces in ℝ3 properly projecting into ℝ2 ’, J. Differential Geom. 90(3) (2012), 351–381.Google Scholar
Alarcón, A. and López, F. J., ‘Properness of associated minimal surfaces’, Trans. Amer. Math. Soc. 366(10) (2014), 5139–5154.Google Scholar
Alarcón, A. and López, F. J., ‘Approximation theory for nonorientable minimal surfaces and applications’, Geom. Topol. 19(2) (2015), 1015–1062.Google Scholar
Alarcón, A. and López, F. J., ‘Complete bounded embedded complex curves in ℂ2 ’, J. Eur. Math. Soc. (JEMS) 18(8) (2016), 1675–1705.Google Scholar
Barbosa, J. L. and do Carmo, M., ‘On the size of a stable minimal surface in R 3 ’, Amer. J. Math. 98(2) (1976), 515–528.Google Scholar
Bell, S. R. and Narasimhan, R., ‘Proper holomorphic mappings of complex spaces’, in: Several Complex Variables, VI, Encyclopaedia of Mathematical Sciences, 69 (Springer, Berlin, 1990), 1–38.Google Scholar
Božin, V., ‘Note on harmonic maps’, Int. Math. Res. Not. IMRN 19 (1999), 1081–1085.Google Scholar
Colding, T. H. and Minicozzi, W. P. II, ‘Minimal surfaces’, in: Courant Lecture Notes in Mathematics, Courant Institute of Mathematical Sciences, 4 (New York University, New York, 1999).Google Scholar
Colding, T. H. and Minicozzi, W. P. II, ‘The Calabi–Yau conjectures for embedded surfaces’, Ann. of Math. (2) 167(1) (2008), 211–243.Google Scholar
Colding, T. H. and Minicozzi, W. P. II, A Course in Minimal Surfaces, Graduate Studies in Mathematics, 121 (American Mathematical Society, Providence, RI, 2011).Google Scholar
Collin, P., ‘Topologie et courbure des surfaces minimales proprement plongées de R 3 ’, Ann. of Math. (2) 145(1) (1997), 1–31.Google Scholar
Collin, P., Kusner, R., Meeks, W. H. III and Rosenberg, H., ‘The topology, geometry and conformal structure of properly embedded minimal surfaces’, J. Differential Geom. 67(2) (2004), 377–393.Google Scholar
Dierkes, U., Hildebrandt, S., Küster, A. and Wohlrab, O., Minimal Surfaces. II Boundary Regularity, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 296 (Springer, Berlin, 1992).Google Scholar
do Carmo, M. P., Differential Geometry of Curves and Surfaces (Prentice-Hall, Englewood Cliffs, NJ, 1976).Google Scholar
Donaldson, S., Riemann Surfaces, Oxford Graduate Texts in Mathematics, 22 (Oxford University Press, Oxford, 2011).Google Scholar
Dor, A., ‘A domain in C m not containing any proper image of the unit disc’, Math. Z. 222(4) (1996), 615–625.Google Scholar
Douglas, J., ‘One-sided minimal surfaces with a given boundary’, Trans. Amer. Math. Soc. 34(4) (1932), 731–756.Google Scholar
Drinovec Drnovšek, B. and Forstnerič, F., ‘Holomorphic curves in complex spaces’, Duke Math. J. 139(2) (2007), 203–253.Google Scholar
Drinovec Drnovšek, B. and Forstnerič, F., ‘The Poletsky–Rosay theorem on singular complex spaces’, Indiana Univ. Math. J. 61(4) (2012), 1407–1423.Google Scholar
Drinovec Drnovšek, B. and Forstnerič, F., ‘Minimal hulls of compact sets in ℝ3 ’, Trans. Amer. Math. Soc. 368(10) (2016), 7477–7506.Google Scholar
Farkas, H. M. and Kra, I., Riemann Surfaces, 2nd edn, Graduate Texts in Mathematics, 71 (Springer, New York, 1992).Google Scholar
Ferrer, L., Martín, F. and Meeks, W. H. III, ‘Existence of proper minimal surfaces of arbitrary topological type’, Adv. Math. 231(1) (2012), 378–413.Google Scholar
Florack, H., ‘Reguläre und meromorphe Funktionen auf nicht geschlossenen Riemannschen Flächen’, Schr. Math. Inst. Univ. Münster 34(1) 1948.Google Scholar
Fornæss, J. E., Forstnerič, F. and Wold, E. F., ‘Holomorphic approximation: the legacy of Weierstrass, Runge, Oka–Weil, and Mergelyan’, Preprint, 2018, arXiv:1802.03924.Google Scholar
Forster, O., ‘Plongements des variétés de Stein’, Comment. Math. Helv. 45 (1970), 170–184.Google Scholar
Forster, O., Lectures on Riemann Surfaces, Graduate Texts in Mathematics, 81 (Springer, New York, 1981), (translated from the German by Bruce Gilligan).Google Scholar
Forstnerič, F., ‘Manifolds of holomorphic mappings from strongly pseudoconvex domains’, Asian J. Math. 11(1) (2007), 113–126.Google Scholar
Forstnerič, F., ‘Oka manifolds: from Oka to Stein and back’, Ann. Fac. Sci. Toulouse Math. (6) 22(4) (2013), 747–809; with an appendix by Finnur Lárusson.Google Scholar
Forstnerič, F., ‘Proper holomorphic immersions into Stein manifolds with the density property’, J. Anal. Math. (to appear) arXiv:1703.8594.Google Scholar
Forstnerič, F., ‘Stein manifolds and holomorphic mappings’, in: The Homotopy Principle in Complex Analysis, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, 56 (Springer, Berlin, 2017).Google Scholar
Forstnerič, F. and Globevnik, J., ‘Proper holomorphic discs in ℂ2 ’, Math. Res. Lett. 8(3) (2001), 257–274.Google Scholar
Forstnerič, F. and Lárusson, F., ‘Survey of Oka theory’, New York J. Math. 17A (2011), 11–38.Google Scholar
Forstnerič, F. and Lárusson, F., ‘The parametric h-principle for minimal surfaces in ℝ n and null curves in ℂ n ’, Comm. Anal. Geom. 27(2) (2019), (to appear) arXiv:1602.01529.Google Scholar
Forstnerič, F. and Wold, E. F., ‘Bordered Riemann surfaces in ℂ2 ’, J. Math. Pures Appl. (9) 91(1) (2009), 100–114.Google Scholar
Forstnerič, F. and Wold, E. F., ‘Embeddings of infinitely connected planar domains into ℂ2 ’, Anal. PDE 6(2) (2013), 499–514.Google Scholar
Fujimoto, H., ‘On the Gauss map of a complete minimal surface in R m ’, J. Math. Soc. Japan 35(2) (1983), 279–288.Google Scholar
Fujimoto, H., ‘On the number of exceptional values of the Gauss maps of minimal surfaces’, J. Math. Soc. Japan 40(2) (1988), 235–247.Google Scholar
Fujimoto, H., ‘Modified defect relations for the Gauss map of minimal surfaces. II’, J. Differential Geom. 31(2) (1990), 365–385.Google Scholar
Globevnik, J., ‘A complete complex hypersurface in the ball of ℂ N ’, Ann. of Math. (2) 182(3) (2015), 1067–1091.Google Scholar
Grauert, H., ‘Holomorphe Funktionen mit Werten in komplexen Lieschen Gruppen’, Math. Ann. 133 (1957), 450–472.Google Scholar
Grauert, H., ‘Analytische Faserungenüber holomorph-vollständigen Räumen’, Math. Ann. 135 (1958), 263–273.Google Scholar
Grauert, H. and Remmert, R., Theory of Stein Spaces, Grundlehren Math. Wiss., 236 (Springer, Berlin–New York, 1979), (translated from the German by Alan Huckleberry).Google Scholar
Grigor’yan, A., ‘Analytic and geometric background of recurrence and non-explosion of the Brownian motion on Riemannian manifolds’, Bull. Amer. Math. Soc. (N.S.) 36(2) (1999), 135–249.Google Scholar
Gromov, M., Partial Differential Relations, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)] (Springer, Berlin, 1986).Google Scholar
Gromov, M., ‘Oka’s principle for holomorphic sections of elliptic bundles’, J. Amer. Math. Soc. 2(4) (1989), 851–897.Google Scholar
Gromov, M., ‘Geometric, algebraic, and analytic descendants of Nash isometric embedding theorems’, Bull. Amer. Math. Soc. (N.S.) 54(2) (2017), 173–245.Google Scholar
Gromov, M. L., ‘Convex integration of differential relations. I’, Izv. Akad. Nauk SSSR Ser. Mat. 37 (1973), 329–343.Google Scholar
Gunning, R. C. and Rossi, H., Analytic Functions of Several Complex Variables (AMS Chelsea Publishing, Providence, RI, 2009), Reprint of the 1965 original.Google Scholar
Hoffman, D. and Meeks, W. H. III, ‘The strong halfspace theorem for minimal surfaces’, Invent. Math. 101(2) (1990), 373–377.Google Scholar
Hoffman, D. A. and Osserman, R., ‘The geometry of the generalized Gauss map’, Mem. Amer. Math. Soc. 28(236) (1980), iii+105.Google Scholar
Hörmander, L., An Introduction to Complex Analysis in Several Variables, 3rd edn, North-Holland Mathematical Library, 7 (North-Holland Publishing, Amsterdam, 1990).Google Scholar
Jones, P. W., ‘A complete bounded complex submanifold of C 3 ’, Proc. Amer. Math. Soc. 76(2) (1979), 305–306.Google Scholar
Jorge, L. P. d. M. and Xavier, F., ‘A complete minimal surface in ℝ3 between two parallel planes’, Ann. of Math. (2) 112(1) (1980), 203–206.Google Scholar
Kobayashi, S. and Eells, J. Jr, Proceedings of the United States-Japan Seminar in Differential Geometry, Kyoto, Japan, 1965 (Nippon Hyoronsha, Tokyo, 1966).Google Scholar
López, F. J., ‘Exotic minimal surfaces’, J. Geom. Anal. 24(2) (2014), 988–1006.Google Scholar
López, F. J., ‘Uniform approximation by complete minimal surfaces of finite total curvature in ℝ3 ’, Trans. Amer. Math. Soc. 366(12) (2014), 6201–6227.Google Scholar
López, F. J. and Pérez, J., ‘Parabolicity and Gauss map of minimal surfaces’, Indiana Univ. Math. J. 52(4) (2003), 1017–1026.Google Scholar
López, F. J. and Ros, A., ‘On embedded complete minimal surfaces of genus zero’, J. Differential Geom. 33(1) (1991), 293–300.Google Scholar
Martín, F., Meeks, W. H. III and Nadirashvili, N., ‘Bounded domains which are universal for minimal surfaces’, Amer. J. Math. 129(2) (2007), 455–461.Google Scholar
Martín, F. and Morales, S., ‘On the asymptotic behavior of a complete bounded minimal surface in ℝ3 ’, Trans. Amer. Math. Soc. 356(10) (2004), 3985–3994.Google Scholar
Martín, F. and Morales, S., ‘Complete proper minimal surfaces in convex bodies of ℝ3 ’, Duke Math. J. 128(3) (2005), 559–593.Google Scholar
Martín, F. and Morales, S., ‘Complete proper minimal surfaces in convex bodies of ℝ3 . II. The behavior of the limit set’, Comment. Math. Helv. 81(3) (2006), 699–725.Google Scholar
Meeks, W. H. III, ‘The classification of complete minimal surfaces in ℝ3 with total curvature greater than - 8𝜋’, Duke Math. J. 48(3) (1981), 523–535.Google Scholar
Meeks, W. H. III and Pérez, J., ‘Conformal properties in classical minimal surface theory’, in: Surveys in Differential Geometry, Surveys in Differential Geometry, IX (International Press, Somerville, MA, 2004), 275–335.Google Scholar
Meeks, W. H. III and Pérez, J., A Survey on Classical Minimal Surface Theory, University Lecture Series, 60 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Meeks, W. H. III, Pérez, J. and Ros, A., ‘The embedded Calabi–Yau conjectures for finite genus’, Preprint, http://www.ugr.es/local/jperez/papers/papers.htm.Google Scholar
Meeks, W. H. III, Pérez, J. and Ros, A., ‘Properly embedded minimal planar domains’, Ann. of Math. (2) 181(2) (2015), 473–546.Google Scholar
Meeks, W. H., ‘III and H. Rosenberg. The uniqueness of the helicoid’, Ann. of Math. (2) 161(2) (2005), 727–758.Google Scholar
Morales, S., ‘On the existence of a proper minimal surface in ℝ3 with a conformal type of disk’, Geom. Funct. Anal. 13(6) (2003), 1281–1301.Google Scholar
Nadirashvili, N., ‘Hadamard’s and Calabi–Yau’s conjectures on negatively curved and minimal surfaces’, Invent. Math. 126(3) (1996), 457–465.Google Scholar
Nash, J., ‘ C 1 isometric imbeddings’, Ann. of Math. (2) 60 (1954), 383–396.Google Scholar
Nash, J., ‘The imbedding problem for Riemannian manifolds’, Ann. of Math. (2) 63 (1956), 20–63.Google Scholar
Nitsche, J. C. C., ‘Lectures on minimal surfaces’, Introduction, Fundamentals, Geometry and Basic Boundary Value Problems, Vol. 1 (Cambridge University Press, Cambridge, 1989), (translated from the German by Jerry M. Feinberg, with a German foreword).Google Scholar
Osserman, R., ‘Global properties of minimal surfaces in E 3 and E n ’, Ann. of Math. (2) 80 (1964), 340–364.Google Scholar
Osserman, R., ‘Minimal surfaces, Gauss maps, total curvature, eigenvalue estimates, and stability’, in: The Chern Symposium 1979 (Proc. Internat. Sympos., Berkeley, CA, 1979) (Springer, New York–Berlin, 1980), 199–227.Google Scholar
Osserman, R., A Survey of Minimal Surfaces, 2nd edn (Dover Publications Inc, New York, 1986).Google Scholar
Osserman, R. and Ru, M., ‘An estimate for the Gauss curvature of minimal surfaces in R m whose Gauss map omits a set of hyperplanes’, J. Differential Geom. 46(3) (1997), 578–593.Google Scholar
Pérez, J., ‘A new golden age of minimal surfaces’, Notices Amer. Math. Soc. 64(4) (2017), 347–358.Google Scholar
Radó, T., ‘On Plateau’s problem’, Ann. of Math. (2) 31(3) (1930), 457–469.Google Scholar
Ros, A., ‘The Gauss map of minimal surfaces’, in: Differential Geometry, Valencia, 2001 (World Scientific Publishers, River Edge, NJ, 2002), 235–252.Google Scholar
Ru, M., ‘On the Gauss map of minimal surfaces immersed in R n ’, J. Differential Geom. 34(2) (1991), 411–423.Google Scholar
Schoen, R. and Yau, S. T., Lectures on Harmonic Maps, Conference Proceedings and Lecture Notes in Geometry and Topology, II (International Press, Cambridge, MA, 1997).Google Scholar
Spring, D., ‘Convex integration theory’, in: Solutions to the h-Principle in Geometry and Topology, Modern Birkhäuser Classics (Birkhäuser/Springer Basel, AG, Basel, 2010), Reprint of the 1998 edition [MR1488424].Google Scholar
Stout, E. L., ‘Bounded holomorphic functions on finite Riemann surfaces’, Trans. Amer. Math. Soc. 120 (1965), 255–285.Google Scholar
Weierstrass, K., ‘Zur Theorie der eindeutigen analytischen Functionen’, Berl. Abh. 1876 (1876), 11–60.Google Scholar
Wirtinger, W., ‘Eine Determinantenidentität und ihre Anwendung auf analytische Gebilde in euklidischer und Hermitescher Maßbestimmung’, Monatsh. Math. Phys. 44(1) (1936), 343–365.Google Scholar
Yang, P., ‘Curvature of complex submanifolds of C n ’, in: Several Complex Variables (Proc. Sympos. Pure Math., Vol. XXX, Part 2, Williams Coll., Williamstown, MA, 1975 (American Mathematical Society, Providence, RI, 1977), 135–137.Google Scholar
Yau, S.-T., ‘Review of geometry and analysis’, in: Mathematics: Frontiers and Perspectives (American Mathematical Society, Providence, RI, 2000), 353–401.Google Scholar