Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T07:14:44.730Z Has data issue: false hasContentIssue false
  • English
  • Français

On the error estimates for the Rayleigh-Schrödinger series and the Kato-Rellich perturbation series

Part of: General theory of linear operators Approximations and expansions

Published online by Cambridge University Press:  09 April 2009

Rekha P. Kulkarni  and
Balmohan V. Limaye
Rekha P. Kulkarni
Affiliation:
Department of Mathematics and Group of Theoretical Studies, Indian Institute of Technology, Bombay, India
Balmohan V. Limaye
Affiliation:
Department of Mathematics and Group of Theoretical Studies, Indian Institute of Technology, Bombay, India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let λ be a simple eigenvalue of a bounded linear operator T on a Banach space X, and let (Tn) be a resolvent operator approximation of T. For large n, let Sn denote the reduced resolvent associated with Tn and λn, the simple eigenvalue of Tn near λ. It is shown that 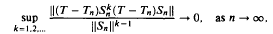under the assumption that all the spectral points of T which are nearest to λ belong to the discrete spectrum of T. This is used to find error estimates for the Rayleigh-Schrödinger series for λ and ϕ with initial terms λn and ϕn, where P (respectively, ϕn) is an eigenvector of T (respectively, Tn) corresponding to λ (respectively, λn), and for the Kato-Rellich perturbation series for PPn, where P (respectively, Pn) is the spectral projection for T (respectively, Tn) associated with λ (respectively, λn).

MSC classification

Secondary: 41A25: Rate of convergence, degree of approximation 41A35: Approximation by operators (in particular, by integral operators) 41A65: Abstract approximation theory (approximation in normed linear spaces and other abstract spaces) 47A70: (Generalized) eigenfunction expansions; rigged Hilbert spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 46 , Issue 3 , June 1989 , pp. 456 - 468
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Anselone, P. M., Collectively compact operator approximation theory (Prentice-Hall, Englewood Cliffs, N.J., 1971).Google Scholar
[2]Chatelin, F., Spectral approximation of linear operators (Academic Press, New York, 1983).Google Scholar
[3]Chatelin, F. and Lemordant, J., ‘Error bounds in the approximation of differential and integral operators’, J. Math. Anal. Appl. 62 (1978), 257–271.CrossRefGoogle Scholar
[4]Kulkarni, R. P. and Limaye, B. V., ‘On the steps of convergence of approximate eigenvectors in the Rayleigh-Schrödinger series’, Numer. Math. 42 (1983), 31–50.CrossRefGoogle Scholar
[5]Kulkarni, R. P. and Limaye, B. V., ‘Geometric and semi-geometric approximation of spectral projections’, J. Math. Anal. Appl. 101 (1984), 139–159.CrossRefGoogle Scholar
[6]Limaye, B. V. and Nair, M. T., ‘On the accuracy of the Rayleigh-Schrödinger approximations’, J. Math. Anal. Appl., to appear.Google Scholar
[7]Nair, M. T., Approximation and localization of eigenelements (Ph.D. Thesis, Indian Institute of Technology, Bombay, 1984).Google Scholar
[8]Redont, P., Application de la théorie de la perturbation des opérateurs linéaires à l'obtention de bornes d'errurs sur les éléments propres et à leur calcul (Thèse de Docteur-Ingénieur, Université de Grenoble, France, 1979).Google Scholar
[9]Taylor, A. E. and Lay, D. C., Introduction to functional analysis, 2nd ed. (John Wiley and Sons, New York, 1980).Google Scholar