Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T04:13:36.951Z Has data issue: false hasContentIssue false
  • English
  • Français

REMARKS ON BIANCHI SUMS AND PONTRJAGIN CLASSES

Part of: Local differential geometry Global differential geometry

Published online by Cambridge University Press:  24 September 2014

MOHAMMED LARBI LABBI
MOHAMMED LARBI LABBI*
Affiliation:
Mathematics Department, College of Science, University of Bahrain, PO Box 32038, Bahrain email mlabbi@uob.edu.bh
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use the exterior and composition products of double forms together with the alternating operator to reformulate Pontrjagin classes and all Pontrjagin numbers in terms of the Riemannian curvature. We show that the alternating operator is obtained by a succession of applications of the first Bianchi sum and we prove some useful identities relating the previous four operations on double forms. As an application, we prove that for a 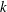$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-conformally flat manifold of dimension 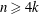$n\geq 4k$, the Pontrjagin classes 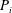$P_i$ vanish for any 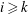$i\geq k$. Finally, we study the equality case in an inequality of Thorpe between the Euler–Poincaré characteristic and the 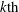$k{\rm th}$ Pontrjagin number of a 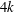$4k$-dimensional Thorpe manifold.

Keywords

double formsBianchi sumThorpe manifoldk-conformally flatPontrjagin numbersPontrjagin classes

MSC classification

Secondary: 53C20: Global Riemannian geometry, including pinching 53B20: Local Riemannian geometry
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 365 - 382
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Avez, A., ‘Characteristic classes and Weyl tensor: applications to general relativity’, Proc. Natl. Acad. Sci. USA 66(2) (1970), 265–268.Google Scholar
Bivens, I., ‘Curvature operators and characteristic classes’, Trans. Amer. Math. Soc. 269(1) (1982), 301–310.Google Scholar
Branson, T. and Gover, A. R., ‘Pontrjagin forms and invariant objects related to the Q-curvature’, Commun. Contemp. Math. 9(335) (2007), 335–358.Google Scholar
Chern, S. S., ‘On the curvature and characteristic classes of a Riemannian manifold’, Abh. Math. Semin. Univ. Hambg. 20 (1956), 117–126.CrossRefGoogle Scholar
Greub, W. H., Multilinear Algebra, 2nd edn (Springer, New York, 1978).CrossRefGoogle Scholar
Greub, W. H., ‘Pontrjagin classes and Weyl tensors’, C. R. Math. Rep. Acad. Sci. Can. III 3 (1981), 177–183.Google Scholar
Hitchin, N., ‘On compact four-dimensional Einstein manifolds’, J. Differential Geom. 9 (1974), 435–441.Google Scholar
Kim, J. M., ‘Einstein–Thorpe manifolds’, PhD Thesis, SUNY at Stony Brook, 1998.Google Scholar
Kim, J. M., ‘8-dimensional Einstein–Thorpe manifolds’, J. Aust. Math. Soc. A 68 (2000), 278–284.Google Scholar
Kulkarni, R. S., ‘On the Bianchi identities’, Math. Ann. 199 (1972), 175–204.CrossRefGoogle Scholar
Labbi, M. L., ‘Double forms, curvature structures and the (p, q)-curvatures’, Trans. Amer. Math. Soc. 357(10) (2005), 3971–3992.Google Scholar
Labbi, M. L., ‘On generalized Einstein metrics’, Balkan J. Geom. Appl. 15(2) (2010), 61–69.Google Scholar
Labbi, M. L., ‘On some algebraic identities and the exterior product of double forms’, Arch. Math. 49(4) (2013), 241–271.Google Scholar
Nasu, T., ‘On conformal invariants of higher order’, Hiroshima Math. J. 5 (1975), 43–60.Google Scholar
Stehney, A., ‘Courbure d’ordre p et les classes de Pontrjagin’, J. Differential Geom. 8 (1973), 125–134.Google Scholar
Thorpe, J. A., ‘Some remarks on the Gauss–Bonnet integral’, J. Math. Mech. 18(8) (1969), 779–786.Google Scholar