Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T13:50:46.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Two weighted ineqalities for maximal functions related to Cesàro convergence

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  09 April 2009

A. L. Bernardis  and
F. J. Martín-Reyes
A. L. Bernardis
Affiliation:
IMAL Güemes 3450 (3000) Santa FeArgentina e-mail: bernard@ceride.gov.ar
F. J. Martín-Reyes
Affiliation:
Departamento de Análisis Matemático Facultad de Ciencias Universidad de Málaga29071 MálagaSpain e-mail: martin@anamat.cie.uma.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterize the pairs of weights (u, v) for which the maximal operator 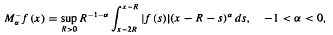is of weak and restricted weak type (p, p) with respect to u(x)dx and v(x)dx. As a consequence we obtain analogous results for 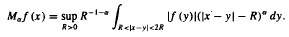We apply the results to the study of the Cesàro-α convergence of singular integrals.

Keywords

Cesàro maximal operatorCesàro- α convergenceweightssingular integrals

MSC classification

Secondary: 42B25: Maximal functions, Littlewood-Paley theory 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.) 42B08: Summability
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 74 , Issue 1 , February 2003 , pp. 111 - 120
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Aimar, H., Forzani, L. and Martín-Reyes, F. J., ‘On weighted inequalities for singular integrals’, Proc. Amer. Math. Soc. 125 (1997), 2057–2064.CrossRefGoogle Scholar
[2]Bernardis, A. L. and Martín-Reyes, F. J., ‘Singular integrals in the Cesàro sense’, J. Fourier Anal. 6 (2000), 143–152.CrossRefGoogle Scholar
[3]Bernardis, A. L. and Martín-Reyes, F. J., ‘Weighted inequalities for a maximal function on the real line’, Proc. Roy. Soc. Edinburgh Sect. A 131 (2001), 267–277.CrossRefGoogle Scholar
[4]García-Cuerva, J. and de Francia, J. L.Rubio, Weighted norm inequalities and related topics, North-Holland Math. Stud., 116; Notas de Matemática (Math. Notes), 104 (North-Holland, Amsterdam, 1985).Google Scholar
[5]Jourkat, W. and Troutman, J., ‘Maximal inequalities related to generalized a.e. continuity’, Trans. Amer Math. Soc. 252 (1979), 49–64.Google Scholar
[6]Martín-Reyes, F. J., ‘New proofs of weighted inequalities for the one-sided Hardy-Littlewood maximal functions’, Proc. Amer Math. Soc. 117 (1993), 691–698.Google Scholar
[7]Sawyer, E., ‘Weighted inequalities for the one-sided Hardy-Littlewood maximal functions’, Trans. Amer Math. Soc. 297 (1986), 53–61.Google Scholar