Research Article
George Szekeres
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-392
-
- Article
-
- You have access
- Export citation
Uniformly weak differentiability of the norm and a condition of Vlasov
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-409
-
- Article
-
- You have access
- Export citation
Signed sums of reciprocals I
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 410-413
-
- Article
-
- You have access
- Export citation
Signed sums of reciprocals II
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 414-417
-
- Article
-
- You have access
- Export citation
On multiplicative representations of integers
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 418-427
-
- Article
-
- You have access
- Export citation
On the fixed points of Sylow subgroups of transitive permutation groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 428-437
-
- Article
-
- You have access
- Export citation
Existence criteria for supplementary difference sets
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 438-446
-
- Article
-
- You have access
- Export citation
Concerning periodicity in the asymptotic behaviour of partition functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 447-456
-
- Article
-
- You have access
- Export citation
Stability of line graphs
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 457-466
-
- Article
-
- You have access
- Export citation
A problem of Paul Erdös on groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 467-472
-
- Article
-
- You have access
- Export citation
The chromatic number of the sphere
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 473-480
-
- Article
-
- You have access
- Export citation
Hadamard matrices of Williamson type
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 481-486
-
- Article
-
- You have access
- Export citation
On the permanent of Schur's matrix
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 487-497
-
- Article
-
- You have access
- Export citation
On the boundedness of multiplicative and positive functionals
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 498-503
-
- Article
-
- You have access
- Export citation
Lattice points in a convex Set of given width
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 504-507
-
- Article
-
- You have access
- Export citation
Strong Carmichael numbers
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 508-510
-
- Article
-
- You have access
- Export citation
Index
Contents
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 511-512
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 21 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 21 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

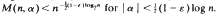 .
.

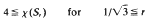
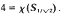
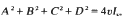
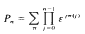
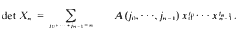
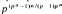 divides
divides