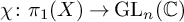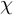1 Introduction
The twisted dynamical zeta functions of Ruelle and Selberg are dynamical zeta functions, which are associated with the geodesic flow on the unit sphere bundle
![]() $S(X)$
of a compact, hyperbolic manifold X. They are defined in terms of the lengths of the closed geodesics, also called length spectrum. The twisted dynamical zeta functions are defined by Euler-type products, which converge in some right half-plane of
$S(X)$
of a compact, hyperbolic manifold X. They are defined in terms of the lengths of the closed geodesics, also called length spectrum. The twisted dynamical zeta functions are defined by Euler-type products, which converge in some right half-plane of
![]() $\mathbb {C}$
. The main goal of this paper is to prove that the twisted Ruelle zeta function associated with an acyclic representation of the fundamental group of X, which is close enough to an acyclic and unitary one, is regular at zero and moreover is equal to the Cappell–Miller torsion as it is introduced in [Reference Cappell and Miller8]. For such representations, there exists a precise relation between the Cappell–Miller torsion and the refined analytic torsion, as it is introduced by Braverman and Kappeler in [Reference Braverman and Kappeler6]. Hence, we conclude that the twisted Ruelle zeta function at zero is equal to the square of the refined analytic torsion multiplied by an exponential, which involves the eta invariant of the even part of the odd-signature operator associated with
$\mathbb {C}$
. The main goal of this paper is to prove that the twisted Ruelle zeta function associated with an acyclic representation of the fundamental group of X, which is close enough to an acyclic and unitary one, is regular at zero and moreover is equal to the Cappell–Miller torsion as it is introduced in [Reference Cappell and Miller8]. For such representations, there exists a precise relation between the Cappell–Miller torsion and the refined analytic torsion, as it is introduced by Braverman and Kappeler in [Reference Braverman and Kappeler6]. Hence, we conclude that the twisted Ruelle zeta function at zero is equal to the square of the refined analytic torsion multiplied by an exponential, which involves the eta invariant of the even part of the odd-signature operator associated with
![]() $\chi $
.
$\chi $
.
Fried’s conjecture and related work
Fried in [Reference Fried18] proved that for a closed, oriented, hyperbolic manifold
![]() $X=\Gamma \backslash {\mathbb {H}}^{d}$
and an acyclic, orthogonal representation
$X=\Gamma \backslash {\mathbb {H}}^{d}$
and an acyclic, orthogonal representation
![]() $\varrho _{1}$
of
$\varrho _{1}$
of
![]() $\pi _{1}(S(X))$
, the Ruelle zeta function, defined for Re
$\pi _{1}(S(X))$
, the Ruelle zeta function, defined for Re
![]() $(s)>d-1$
by
$(s)>d-1$
by
 $$ \begin{align*} R(s;\varrho_{1}):=\prod_{\substack{[\gamma]\neq e,\\ [\gamma]\operatorname{\mathrm{prime}}}}{\det(\operatorname{\mathrm{Id}}-\varrho_{1}(\gamma)e^{-sl(\gamma)}}), \end{align*} $$
$$ \begin{align*} R(s;\varrho_{1}):=\prod_{\substack{[\gamma]\neq e,\\ [\gamma]\operatorname{\mathrm{prime}}}}{\det(\operatorname{\mathrm{Id}}-\varrho_{1}(\gamma)e^{-sl(\gamma)}}), \end{align*} $$
admits a meromorphic extension to
![]() $\mathbb {C}$
, and for
$\mathbb {C}$
, and for
![]() $\epsilon =(-1)^{d-1}$
$\epsilon =(-1)^{d-1}$
where
![]() $\tau _{\varrho _{1}}(S(X))\in \mathbb {R}^{+}$
is the Reidemeister torsion, a topological invariant ([Reference Reidemeister43], [Reference Franz17], [Reference De Rham14]).
$\tau _{\varrho _{1}}(S(X))\in \mathbb {R}^{+}$
is the Reidemeister torsion, a topological invariant ([Reference Reidemeister43], [Reference Franz17], [Reference De Rham14]).
Fried in [Reference Fried19] conjectured that the same result holds for all compact locally homogeneous Riemannian spaces X and acyclic bundles over
![]() $S(X)$
. This conjecture was proved by [Reference Moscovici and Stanton32] and [Reference Shen46] for negatively curved locally symmetric spaces.
$S(X)$
. This conjecture was proved by [Reference Moscovici and Stanton32] and [Reference Shen46] for negatively curved locally symmetric spaces.
Fried, in the same paper, dealt mostly with hyperbolic manifolds of odd dimension. Considering an acyclic, orthogonal representation
![]() $\varrho $
of
$\varrho $
of
![]() $\pi (X)$
and using the Selberg trace formula for the heat operator
$\pi (X)$
and using the Selberg trace formula for the heat operator
![]() $e^{-t\Delta _{j}}$
, where
$e^{-t\Delta _{j}}$
, where
![]() $\Delta _{j}$
is the Hodge Laplacian on j-forms on X with values in the flat vector bundle
$\Delta _{j}$
is the Hodge Laplacian on j-forms on X with values in the flat vector bundle
![]() $E_{\varrho }$
associated with
$E_{\varrho }$
associated with
![]() $\varrho $
, he proved the meromorphic continuation of the zeta functions to the whole complex plane, as well as functional equations for the Selberg zeta function ([Reference Fried18, p. 531-532]). In addition, he proved that
$\varrho $
, he proved the meromorphic continuation of the zeta functions to the whole complex plane, as well as functional equations for the Selberg zeta function ([Reference Fried18, p. 531-532]). In addition, he proved that
![]() $R(0;\varrho )$
is regular at
$R(0;\varrho )$
is regular at
![]() $s=0$
and
$s=0$
and
where
![]() $T_{\varrho }(X)$
is the Ray–Singer analytic torsion defined as in [Reference Ray and Singer42] (see [Reference Fried18, eq. (18)]). By Cheeger–Müller theorem ([Reference Cheeger11], [Reference Müller34]), the analytic torsion
$T_{\varrho }(X)$
is the Ray–Singer analytic torsion defined as in [Reference Ray and Singer42] (see [Reference Fried18, eq. (18)]). By Cheeger–Müller theorem ([Reference Cheeger11], [Reference Müller34]), the analytic torsion
![]() $T_{\varrho }(X)$
is equal to the Reidemeister torsion
$T_{\varrho }(X)$
is equal to the Reidemeister torsion
![]() $\tau _{\varrho }(X)$
. Since
$\tau _{\varrho }(X)$
. Since
![]() $\pi _{1}(S(X))\cong \pi _{1}(X)$
and
$\pi _{1}(S(X))\cong \pi _{1}(X)$
and
![]() $\tau _{\varrho }(X)^{2}=\tau _{\varrho _{1}}(S(X))$
([Reference Fried18, p. 526]), one obtains (1.1). In fact, Fried proved a more general result. If the representation
$\tau _{\varrho }(X)^{2}=\tau _{\varrho _{1}}(S(X))$
([Reference Fried18, p. 526]), one obtains (1.1). In fact, Fried proved a more general result. If the representation
![]() $\varrho $
is not assumed acyclic, then by [Reference Fried18, Theorem 3], the leading term in the Laurent expansion of
$\varrho $
is not assumed acyclic, then by [Reference Fried18, Theorem 3], the leading term in the Laurent expansion of
![]() $R(s;\varrho )$
at
$R(s;\varrho )$
at
![]() $s=0$
is
$s=0$
is
where e is a linear combination of the twisted Betti numbers
![]() $\beta _{i}=\dim H^{i}(X;\varrho )$
, and
$\beta _{i}=\dim H^{i}(X;\varrho )$
, and
![]() $C_{\varrho }\in \mathbb {Q}$
is defined in terms of
$C_{\varrho }\in \mathbb {Q}$
is defined in terms of
![]() $\beta _{i}$
. The theorem of Fried gave rise to important applications, such as the asymptotic behavior of the analytic torsion ([Reference Müller36]) and the study of the growth of the torsion in the cohomology of a closed arithmetic hyperbolic
$\beta _{i}$
. The theorem of Fried gave rise to important applications, such as the asymptotic behavior of the analytic torsion ([Reference Müller36]) and the study of the growth of the torsion in the cohomology of a closed arithmetic hyperbolic
![]() $3$
-manifold ([Reference Marshall and Müller27]).
$3$
-manifold ([Reference Marshall and Müller27]).
The connection of the Ruelle zeta function to spectral invariants such as the analytic torsion has been studied by Bunke and Olbrich ([Reference Bunke and Olbrich7]), Wotzke ([Reference Wotzke52]), Müller ([Reference Müller36]) for compact hyperbolic manifolds, under certain assumptions on the representation of the fundamental group of the manifold. For the case of a hyperbolic manifold of finite volume, we refer the reader to the work of Park ([Reference Park38]) and Pfaff ([Reference Pfaff40], [Reference Pfaff41]). An advanced study of the dynamical zeta functions of locally symmetric manifolds of higher rank is due to Moscovici and Stanton in [Reference Moscovici and Stanton32], Deitmar in [Reference Deitmar15], Shen in [Reference Shen46] and Moscovici, Stanton and Frahm in [Reference Moscovici, Stanton and Frahm33]. We mention also the work of Dang, Guillarmou, Rivière and Shen ([Reference Dan, Guillarmou, Rivière and Shen13]), where the Fried’s conjecture is treated for dimension
![]() $3$
for Anosov flows near the geodesic flow on the unit tangent bundle of hyperbolic
$3$
for Anosov flows near the geodesic flow on the unit tangent bundle of hyperbolic
![]() $3$
-manifolds. This result was extended by Chaubet and Dang to higher dimensions in [Reference Chaubet and Dan10], where a new object is introduced, the dynamical torsion. Cekić, Delarue, Dyatlov and Paternain studied the Ruelle zeta function at zero for nearly hyperbolic 3-manifolds in [Reference Cekić, Delarue, Dyatlov and Paternain9]. The twisted Ruelle zeta function associated with a nonunitary representation and its relation to topological invariants has been studied by Frahm and the author in [Reference Frahm and Spilioti16], in the case of compact hyperbolic surfaces, and by Bénard, Frahm and the author in [Reference Bénard, Frahm and Spilioti3], in the case of compact hyperbolic orbisurfaces. Recently, Hochs and Saratchandran in [Reference Hochs and Saratchandran24] dealt with an equivariant generalisation of Fried’s conjecture for proper group actions on smooth manifolds, with compact quotients.
$3$
-manifolds. This result was extended by Chaubet and Dang to higher dimensions in [Reference Chaubet and Dan10], where a new object is introduced, the dynamical torsion. Cekić, Delarue, Dyatlov and Paternain studied the Ruelle zeta function at zero for nearly hyperbolic 3-manifolds in [Reference Cekić, Delarue, Dyatlov and Paternain9]. The twisted Ruelle zeta function associated with a nonunitary representation and its relation to topological invariants has been studied by Frahm and the author in [Reference Frahm and Spilioti16], in the case of compact hyperbolic surfaces, and by Bénard, Frahm and the author in [Reference Bénard, Frahm and Spilioti3], in the case of compact hyperbolic orbisurfaces. Recently, Hochs and Saratchandran in [Reference Hochs and Saratchandran24] dealt with an equivariant generalisation of Fried’s conjecture for proper group actions on smooth manifolds, with compact quotients.
For unitary representations, the dynamical zeta functions have been studied by Bunke and Olbrich in [Reference Bunke and Olbrich7] for all locally symmetric spaces of real rank 1. They proved that the zeta functions admit a meromorphic continuation to the whole complex plane and satisfy functional equations. Moreover, for compact, hyperbolic, odd-dimensional manifolds, and under the additional assumption that the representation is acyclic, they proved that the Ruelle zeta function is regular at zero and equals the square of the analytic torsion as in Equation (1.2) ([Reference Bunke and Olbrich7, Theorem 4.8]).
Wotzke in [Reference Wotzke52] extended this result for representations of
![]() $\Gamma $
, which are not necessary unitary, but very special ones. In particular, he considered a compact odd-dimensional, hyperbolic, manifold and a finite-dimensional, irreducible, representation
$\Gamma $
, which are not necessary unitary, but very special ones. In particular, he considered a compact odd-dimensional, hyperbolic, manifold and a finite-dimensional, irreducible, representation
![]() $\tau \colon G\rightarrow \operatorname {\mathrm {GL}}(V)$
of G such that
$\tau \colon G\rightarrow \operatorname {\mathrm {GL}}(V)$
of G such that
![]() $\tau \neq \tau _{\theta }$
, where
$\tau \neq \tau _{\theta }$
, where
![]() $\tau _{\theta }=\tau \circ \theta $
and
$\tau _{\theta }=\tau \circ \theta $
and
![]() $\theta $
denotes the Cartan involution of G. Under these assumptions, he proved that the Ruelle zeta function admits a meromorphic continuation to the whole complex plane. In addition, it is regular at zero and
$\theta $
denotes the Cartan involution of G. Under these assumptions, he proved that the Ruelle zeta function admits a meromorphic continuation to the whole complex plane. In addition, it is regular at zero and
where the representation
![]() $\tau $
restricted to
$\tau $
restricted to
![]() $\Gamma $
. Wotzke’s method is based on the fact that if one considers the restrictions
$\Gamma $
. Wotzke’s method is based on the fact that if one considers the restrictions
![]() $\tau |_{K}$
and
$\tau |_{K}$
and
![]() $\tau |_{\Gamma }$
of
$\tau |_{\Gamma }$
of
![]() $\tau $
to K and
$\tau $
to K and
![]() $\Gamma $
, respectively, there is an isomorphism between the locally homogeneous vector bundle
$\Gamma $
, respectively, there is an isomorphism between the locally homogeneous vector bundle
![]() $E_{\tau }$
over X, associated with
$E_{\tau }$
over X, associated with
![]() $\tau |_{K}$
, and the flat vector bundle
$\tau |_{K}$
, and the flat vector bundle
![]() $E_{\operatorname {\mathrm {flat}}}$
over X associated with
$E_{\operatorname {\mathrm {flat}}}$
over X associated with
![]() $\tau |_{\Gamma }$
. By [Reference Matsushima and Murakami28, Lemma 3.1], a Hermitian fiber metric in
$\tau |_{\Gamma }$
. By [Reference Matsushima and Murakami28, Lemma 3.1], a Hermitian fiber metric in
![]() $E_{\tau }$
descends to a fiber metric in
$E_{\tau }$
descends to a fiber metric in
![]() $E_{\operatorname {\mathrm {flat}}}$
. Therefore, one deals with self-adjoint Laplacians and all tools from harmonic analysis on locally symmetric spaces are available.
$E_{\operatorname {\mathrm {flat}}}$
. Therefore, one deals with self-adjoint Laplacians and all tools from harmonic analysis on locally symmetric spaces are available.
Results
We consider an oriented, compact, hyperbolic manifold X of odd dimension d, obtained as follows. Let either
![]() $G=\operatorname {\mathrm {SO}}^{0}(d,1)$
,
$G=\operatorname {\mathrm {SO}}^{0}(d,1)$
,
![]() $K=\operatorname {\mathrm {SO}}(d)$
or
$K=\operatorname {\mathrm {SO}}(d)$
or
![]() $G=\operatorname {\mathrm {Spin}}(d,1)$
,
$G=\operatorname {\mathrm {Spin}}(d,1)$
,
![]() $K=\operatorname {\mathrm {Spin}}(d)$
. Then, K is a maximal compact subgroup of G. Let
$K=\operatorname {\mathrm {Spin}}(d)$
. Then, K is a maximal compact subgroup of G. Let
![]() $\widetilde {X}:=G/K$
. The space
$\widetilde {X}:=G/K$
. The space
![]() $\widetilde {X}$
can be equipped with a G-invariant metric, which is unique up to scaling and is of constant negative curvature. If we normalize this metric such that it has constant negative curvature
$\widetilde {X}$
can be equipped with a G-invariant metric, which is unique up to scaling and is of constant negative curvature. If we normalize this metric such that it has constant negative curvature
![]() $-1$
, then
$-1$
, then
![]() $\widetilde {X}$
, equipped with this metric, is isometric to the d-dimensional hyperbolic space
$\widetilde {X}$
, equipped with this metric, is isometric to the d-dimensional hyperbolic space
![]() ${\mathbb {H}}^{d}$
. Let
${\mathbb {H}}^{d}$
. Let
![]() $\Gamma $
be a discrete torsion-free subgroup of G such that
$\Gamma $
be a discrete torsion-free subgroup of G such that
![]() $\Gamma \backslash G$
is compact. Then,
$\Gamma \backslash G$
is compact. Then,
![]() $\Gamma $
acts by isometries on
$\Gamma $
acts by isometries on
![]() $\widetilde X$
and
$\widetilde X$
and
![]() $X=\Gamma \backslash \widetilde X$
is a compact, oriented, hyperbolic manifold of dimension d. This is a case of a locally symmetric space of noncompact type of real rank 1. This means that in the Iwasawa decomposition
$X=\Gamma \backslash \widetilde X$
is a compact, oriented, hyperbolic manifold of dimension d. This is a case of a locally symmetric space of noncompact type of real rank 1. This means that in the Iwasawa decomposition
![]() $G=KAN$
, A is a multiplicative torus of dimension 1, that is,
$G=KAN$
, A is a multiplicative torus of dimension 1, that is,
![]() $A\cong \mathbb {R}^+$
.
$A\cong \mathbb {R}^+$
.
For a given
![]() $\gamma \in \Gamma $
, we denote by
$\gamma \in \Gamma $
, we denote by
![]() $[\gamma ]$
the
$[\gamma ]$
the
![]() $\Gamma $
-conjugacy class of
$\Gamma $
-conjugacy class of
![]() $\gamma $
. If
$\gamma $
. If
![]() $\gamma \neq e$
, then there is a unique closed geodesic
$\gamma \neq e$
, then there is a unique closed geodesic
![]() $c_{\gamma }$
associated with
$c_{\gamma }$
associated with
![]() $[\gamma ]$
. Let
$[\gamma ]$
. Let
![]() $l(\gamma )$
denote the length of
$l(\gamma )$
denote the length of
![]() $c_{\gamma }$
. The conjugacy class
$c_{\gamma }$
. The conjugacy class
![]() $[\gamma ]$
is called primitive if there exists no
$[\gamma ]$
is called primitive if there exists no
![]() $k\in \mathbb {N}$
with
$k\in \mathbb {N}$
with
![]() $k>1$
and
$k>1$
and
![]() $\gamma _{0}\in \Gamma $
such that
$\gamma _{0}\in \Gamma $
such that
![]() $\gamma =\gamma _{0}^{k}$
. The prime closed geodesics correspond to the primitive conjugacy classes and are those geodesics that trace out their image exactly once. Let M be the centralizer of A in K. Since
$\gamma =\gamma _{0}^{k}$
. The prime closed geodesics correspond to the primitive conjugacy classes and are those geodesics that trace out their image exactly once. Let M be the centralizer of A in K. Since
![]() $\Gamma $
is a cocompact subgroup of G, every element
$\Gamma $
is a cocompact subgroup of G, every element
![]() $\gamma \in \Gamma -\{e\}$
is hyperbolic. Then, by [Reference Wallach51, Lemma 6.5], there exist a
$\gamma \in \Gamma -\{e\}$
is hyperbolic. Then, by [Reference Wallach51, Lemma 6.5], there exist a
![]() $g\in G$
, a
$g\in G$
, a
![]() $m_{\gamma } \in M$
and an
$m_{\gamma } \in M$
and an
![]() $a_{\gamma } \in A$
such that
$a_{\gamma } \in A$
such that
![]() $ g^{-1}\gamma g=m_{\gamma }a_{\gamma }$
. The element
$ g^{-1}\gamma g=m_{\gamma }a_{\gamma }$
. The element
![]() $m_{\gamma }$
is determined up to conjugacy in M, and the element
$m_{\gamma }$
is determined up to conjugacy in M, and the element
![]() $a_{\gamma }$
depends only on
$a_{\gamma }$
depends only on
![]() $\gamma $
.
$\gamma $
.
Let
![]() $\mathfrak {g},\mathfrak {a}$
be the Lie algebras of G and A, respectively. Let
$\mathfrak {g},\mathfrak {a}$
be the Lie algebras of G and A, respectively. Let
![]() $\Delta ^{+}(\mathfrak {g},\mathfrak {a})$
be the set of positive roots of
$\Delta ^{+}(\mathfrak {g},\mathfrak {a})$
be the set of positive roots of
![]() $(\mathfrak {g},\mathfrak {a})$
. Then,
$(\mathfrak {g},\mathfrak {a})$
. Then,
![]() $\Delta ^{+}(\mathfrak {g},\mathfrak {a})$
consists of a single root
$\Delta ^{+}(\mathfrak {g},\mathfrak {a})$
consists of a single root
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\mathfrak {g}_{\alpha }$
be the corresponding root space. Let
$\mathfrak {g}_{\alpha }$
be the corresponding root space. Let
![]() $\overline {\mathfrak {n}}$
be the negative root space of
$\overline {\mathfrak {n}}$
be the negative root space of
![]() $(\mathfrak {g},\mathfrak {a})$
. Let
$(\mathfrak {g},\mathfrak {a})$
. Let
![]() $S^k(\operatorname {\mathrm {Ad}}(m_\gamma a_\gamma )|_{\overline {\mathfrak {n}}})$
be the k-th symmetric power of the adjoint map
$S^k(\operatorname {\mathrm {Ad}}(m_\gamma a_\gamma )|_{\overline {\mathfrak {n}}})$
be the k-th symmetric power of the adjoint map
![]() $\operatorname {\mathrm {Ad}}(m_\gamma a_\gamma )$
restricted to
$\operatorname {\mathrm {Ad}}(m_\gamma a_\gamma )$
restricted to
![]() $\overline {\mathfrak {n}}$
and
$\overline {\mathfrak {n}}$
and
![]() $\rho $
be defined as
$\rho $
be defined as
![]() $\rho :=\frac {1}{2}\dim (\mathfrak {g}_\alpha )\alpha $
. We define the twisted zeta functions associated with unitary, irreducible representations
$\rho :=\frac {1}{2}\dim (\mathfrak {g}_\alpha )\alpha $
. We define the twisted zeta functions associated with unitary, irreducible representations
![]() $\sigma $
of M and finite-dimensional, complex representations
$\sigma $
of M and finite-dimensional, complex representations
![]() $\chi $
of
$\chi $
of
![]() $\Gamma $
. The twisted Selberg zeta function
$\Gamma $
. The twisted Selberg zeta function
![]() $Z(s;\sigma ,\chi )$
is defined for
$Z(s;\sigma ,\chi )$
is defined for
![]() $s\in \mathbb {C}$
by the infinite product
$s\in \mathbb {C}$
by the infinite product
 $$ \begin{align} Z(s;\sigma,\chi):=\prod_{\substack{[\gamma]\neq e,\\ [\gamma]\operatorname{\mathrm{prime}}}} \prod_{k=0}^{\infty}\det\Big(\operatorname{\mathrm{Id}}-\big(\chi(\gamma) \otimes\sigma(m_\gamma)\otimes S^k(\operatorname{\mathrm{Ad}}(m_\gamma a_\gamma)|_{\overline{\mathfrak{n}}})\big)e^{-(s+|\rho|)l(\gamma)}\Big). \end{align} $$
$$ \begin{align} Z(s;\sigma,\chi):=\prod_{\substack{[\gamma]\neq e,\\ [\gamma]\operatorname{\mathrm{prime}}}} \prod_{k=0}^{\infty}\det\Big(\operatorname{\mathrm{Id}}-\big(\chi(\gamma) \otimes\sigma(m_\gamma)\otimes S^k(\operatorname{\mathrm{Ad}}(m_\gamma a_\gamma)|_{\overline{\mathfrak{n}}})\big)e^{-(s+|\rho|)l(\gamma)}\Big). \end{align} $$
The twisted Ruelle zeta function
![]() $R(s;\sigma ,\chi )$
is defined for
$R(s;\sigma ,\chi )$
is defined for
![]() $s\in \mathbb {C}$
by the infinite product
$s\in \mathbb {C}$
by the infinite product
 $$ \begin{align} R(s;\sigma,\chi):=\prod_{\substack{[\gamma]\neq{e}\\ [\gamma]\operatorname{\mathrm{prime}}}}\det(\operatorname{\mathrm{Id}}-(\chi(\gamma)\otimes\sigma(m_{\gamma}))e^{-sl(\gamma)}). \end{align} $$
$$ \begin{align} R(s;\sigma,\chi):=\prod_{\substack{[\gamma]\neq{e}\\ [\gamma]\operatorname{\mathrm{prime}}}}\det(\operatorname{\mathrm{Id}}-(\chi(\gamma)\otimes\sigma(m_{\gamma}))e^{-sl(\gamma)}). \end{align} $$
Both
![]() $Z(s;\sigma ,\chi )$
and
$Z(s;\sigma ,\chi )$
and
![]() $R(s;\sigma ,\chi )$
converge absolutely and uniformly on compact subsets of some half-plane of
$R(s;\sigma ,\chi )$
converge absolutely and uniformly on compact subsets of some half-plane of
![]() $\mathbb {C}$
([Reference Spilioti48, Proposition 3.4 and Proposition 3.5]).
$\mathbb {C}$
([Reference Spilioti48, Proposition 3.4 and Proposition 3.5]).
In [Reference Spilioti48], it was proved that the twisted dynamical zeta functions associated with a general, finite-dimensional, complex representation of the fundamental group, as in in Equations (1.3) and (1.4), admit a meromorphic continuation to the whole complex plane. In [Reference Spilioti49], the functional equations for them are derived. Moreover, it is shown a determinant formula, which relates the twisted Ruelle zeta function with a finite product of graded regularized determinants of certain, twisted (non-self-adjoint), elliptic differential operators (see [Reference Spilioti49, Proposition 7.9, case (a)]). These results extend the results of Bunke and Olbrich to the case of nonunitary twists. The determinant formula is the keypoint to prove our main results, Theorem 1, Theorem 2 and Corollary 1, below.
In the present paper, we consider acyclic representations of
![]() $\Gamma $
, which are nonunitary but closed enough to unitary ones. We provide here some details about these representations. For a compact, oriented, odd-dimensional, Riemannian manifold
$\Gamma $
, which are nonunitary but closed enough to unitary ones. We provide here some details about these representations. For a compact, oriented, odd-dimensional, Riemannian manifold
![]() $(X,g)$
and a complex vector bundle
$(X,g)$
and a complex vector bundle
![]() $E\rightarrow X$
, equipped with a flat connection
$E\rightarrow X$
, equipped with a flat connection
![]() $\nabla $
, Braverman and Kappeler in [Reference Braverman and Kappeler6] considered the odd signature operator
$\nabla $
, Braverman and Kappeler in [Reference Braverman and Kappeler6] considered the odd signature operator
![]() $B=(\nabla ,g)$
, acting on the space of smooth differential forms
$B=(\nabla ,g)$
, acting on the space of smooth differential forms
![]() $\Lambda ^{k}(X,E)$
on X, with values in E (see Section 6.2 in [Reference Braverman and Kappeler6] and Section 6.1 in the present paper). This is a first-order, elliptic differential operator, which is in general non-self-adjoint. Suppose that there exists a Hermitian metric on E, which is preserved by
$\Lambda ^{k}(X,E)$
on X, with values in E (see Section 6.2 in [Reference Braverman and Kappeler6] and Section 6.1 in the present paper). This is a first-order, elliptic differential operator, which is in general non-self-adjoint. Suppose that there exists a Hermitian metric on E, which is preserved by
![]() $\nabla $
. In such a case, we say that
$\nabla $
. In such a case, we say that
![]() $\nabla $
is a Hermitian connection. Then, the operator is (formally) self-adjoint. Hence, if we assume further that
$\nabla $
is a Hermitian connection. Then, the operator is (formally) self-adjoint. Hence, if we assume further that
![]() $\nabla $
is acyclic, that is,
$\nabla $
is acyclic, that is,
![]() $\operatorname {\mathrm {Im}}(\nabla |_{\Lambda ^{k-1}(X,E)})=\operatorname {\mathrm {Ker}}(\nabla |_{\Lambda ^{k}(X,E)})$
, for every k, the odd signature operator B is bijective. If there is no Hermitian metric on E, which is preserved by
$\operatorname {\mathrm {Im}}(\nabla |_{\Lambda ^{k-1}(X,E)})=\operatorname {\mathrm {Ker}}(\nabla |_{\Lambda ^{k}(X,E)})$
, for every k, the odd signature operator B is bijective. If there is no Hermitian metric on E, which is preserved by
![]() $\nabla $
, then the odd signature operator is no longer self-adjoint. One can assume that
$\nabla $
, then the odd signature operator is no longer self-adjoint. One can assume that
![]() $\nabla $
is acyclic, but this does not imply that the odd signature operator has a trivial kernel since Hodge theory is no longer applicable.
$\nabla $
is acyclic, but this does not imply that the odd signature operator has a trivial kernel since Hodge theory is no longer applicable.
However, by a continuity argument, [Reference Braverman and Kappeler6, Proposition 6.8], the following assumptions
Assumption 1. The connection
![]() $\nabla $
is acyclic, that is, for every k,
$\nabla $
is acyclic, that is, for every k,
![]() $\operatorname {\mathrm {Im}}(\nabla |_{\Lambda ^{k-1}(X,E)})=\operatorname {\mathrm {Ker}}(\nabla |_{\Lambda ^{k}(X,E)})$
;
$\operatorname {\mathrm {Im}}(\nabla |_{\Lambda ^{k-1}(X,E)})=\operatorname {\mathrm {Ker}}(\nabla |_{\Lambda ^{k}(X,E)})$
;
Assumption 2. The odd signature operator
![]() $B\colon \Lambda ^{k}(X,E)\rightarrow \Lambda ^{k}(X,E)$
is bijective; are satisfied for all flat connections in an open neighbourhood, in a suitable
$B\colon \Lambda ^{k}(X,E)\rightarrow \Lambda ^{k}(X,E)$
is bijective; are satisfied for all flat connections in an open neighbourhood, in a suitable
![]() $C^{0}$
-topology (see Subsection 6.2), of the set of acyclic, Hermitian connections.
$C^{0}$
-topology (see Subsection 6.2), of the set of acyclic, Hermitian connections.
Let
![]() $\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all n-dimensional, complex representations of
$\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all n-dimensional, complex representations of
![]() $\pi _{1}(X)$
. This set has a natural structure of a complex algebraic variety (see Subsection 6.3). Each representation
$\pi _{1}(X)$
. This set has a natural structure of a complex algebraic variety (see Subsection 6.3). Each representation
![]() $\chi \in \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
gives rise to a vector bundle
$\chi \in \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
gives rise to a vector bundle
![]() $E_{\chi }$
with a flat connection
$E_{\chi }$
with a flat connection
![]() $\nabla _{\chi }$
, whose monodromy is isomorphic to
$\nabla _{\chi }$
, whose monodromy is isomorphic to
![]() $\chi $
. Let
$\chi $
. Let
![]() $\operatorname {\mathrm {Rep}}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all acyclic representations of
$\operatorname {\mathrm {Rep}}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all acyclic representations of
![]() $\pi _{1}(X)$
, that is, the set of representations
$\pi _{1}(X)$
, that is, the set of representations
![]() $\chi $
such that
$\chi $
such that
![]() $\nabla _{\chi }$
is acyclic. Let
$\nabla _{\chi }$
is acyclic. Let
![]() $\operatorname {\mathrm {Rep}}^{u}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all unitary representations of
$\operatorname {\mathrm {Rep}}^{u}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all unitary representations of
![]() $\pi _{1}(X)$
, that is, the set of representations such that there exists a Hermitian scalar product
$\pi _{1}(X)$
, that is, the set of representations such that there exists a Hermitian scalar product
![]() $(\cdot ,\cdot )$
on
$(\cdot ,\cdot )$
on
![]() $\mathbb {C}^{n}$
, which is preserved by the matrices
$\mathbb {C}^{n}$
, which is preserved by the matrices
![]() $\chi (\gamma )$
, for all
$\chi (\gamma )$
, for all
![]() $\gamma \in \pi _{1}(X)$
. We set
$\gamma \in \pi _{1}(X)$
. We set
Let
![]() $B_{\chi }:=B(\nabla _{\chi },g)\colon \Lambda ^{k}(X,E)\rightarrow \Lambda ^{k}(X,E)$
. Let
$B_{\chi }:=B(\nabla _{\chi },g)\colon \Lambda ^{k}(X,E)\rightarrow \Lambda ^{k}(X,E)$
. Let
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
be the restriction of
$B_{\chi }^{\operatorname {\mathrm {even}}}$
be the restriction of
![]() $B_{\chi }$
to
$B_{\chi }$
to
![]() $\Lambda ^{\operatorname {\mathrm {even}}}(X,E)$
. Suppose that for some representation
$\Lambda ^{\operatorname {\mathrm {even}}}(X,E)$
. Suppose that for some representation
![]() $\chi _{0}\in \operatorname {\mathrm {Rep}}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
the operator
$\chi _{0}\in \operatorname {\mathrm {Rep}}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
the operator
![]() $B_{\chi _{0}}$
bijective. Then, there exists an open neighbourhood (in classical topology)
$B_{\chi _{0}}$
bijective. Then, there exists an open neighbourhood (in classical topology)
![]() $V \subset \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
of the set
$V \subset \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
of the set
![]() $\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
of acyclic, unitary representations such that, for all
$\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
of acyclic, unitary representations such that, for all
![]() $\chi \in V$
, the pair
$\chi \in V$
, the pair
![]() $(\nabla _{\chi },g)$
satisfies Assumptions 1 and 2. For such representations Braverman and Kappeler defined a Riemannian metric-invariant, the refined analytic torsion, which is a nonzero complex number, defined by
$(\nabla _{\chi },g)$
satisfies Assumptions 1 and 2. For such representations Braverman and Kappeler defined a Riemannian metric-invariant, the refined analytic torsion, which is a nonzero complex number, defined by
Here,
![]() $\theta \in (-\pi ,0)$
is an Agmon angle for
$\theta \in (-\pi ,0)$
is an Agmon angle for
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
,
$B_{\chi }^{\operatorname {\mathrm {even}}}$
,
![]() ${\det }_{\operatorname {\mathrm {gr}},\theta }(B_{\chi }^{\operatorname {\mathrm {even}}})$
denotes the graded determinant of
${\det }_{\operatorname {\mathrm {gr}},\theta }(B_{\chi }^{\operatorname {\mathrm {even}}})$
denotes the graded determinant of
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
(see Remark 7.1.2), and
$B_{\chi }^{\operatorname {\mathrm {even}}}$
(see Remark 7.1.2), and
![]() $\eta _{tr}(g)=\frac {1}{2}\eta (0, B_{tr}(g))$
, where
$\eta _{tr}(g)=\frac {1}{2}\eta (0, B_{tr}(g))$
, where
![]() $\eta (0, B_{tr}(g))$
denotes the eta invariant of the even part of the odd signature operator corresponding to the trivial line bundle, endowed with the trivial connection (see Definition 4.1.1). One can view this definition as a special case of the definition of the refined analytic torsion as an element of the determinant line in [Reference Braverman and Kappeler4], where the assumption of the bijectivity of the odd signature operator is removed.
$\eta (0, B_{tr}(g))$
denotes the eta invariant of the even part of the odd signature operator corresponding to the trivial line bundle, endowed with the trivial connection (see Definition 4.1.1). One can view this definition as a special case of the definition of the refined analytic torsion as an element of the determinant line in [Reference Braverman and Kappeler4], where the assumption of the bijectivity of the odd signature operator is removed.
On the other hand, Cappell and Miller in [Reference Cappell and Miller8], defined another invariant, the Cappell–Miller torsion
![]() $\tau \in \det (H^{*}(X,E))\otimes \det (H^{*}(X,E))$
. In this setting, the regularized determinants of the flat Hodge Laplacians are equipped. To define the flat Laplacians, no use of a Hermitian metric on the flat vector bundle is needed (see Section 9). These operators coincide with the square
$\tau \in \det (H^{*}(X,E))\otimes \det (H^{*}(X,E))$
. In this setting, the regularized determinants of the flat Hodge Laplacians are equipped. To define the flat Laplacians, no use of a Hermitian metric on the flat vector bundle is needed (see Section 9). These operators coincide with the square
![]() $B^{2}$
of the odd signature operator B. If
$B^{2}$
of the odd signature operator B. If
![]() $\chi \in V$
, the element of
$\chi \in V$
, the element of
![]() $\det (H^{*}(X,E_{\chi }))\otimes \det (H^{*}(X,E_{\chi }))$
does not contribute in the definition (see Definition 9.2). In such a case, the Cappell–Miller torsion
$\det (H^{*}(X,E_{\chi }))\otimes \det (H^{*}(X,E_{\chi }))$
does not contribute in the definition (see Definition 9.2). In such a case, the Cappell–Miller torsion
![]() $\tau _{\chi }$
is a complex number given by
$\tau _{\chi }$
is a complex number given by
 $$ \begin{align*} \tau_{\chi}:=\prod_{k=0}^{d} \det(B_{\chi,k}^{2})^{k(-1)^{k+1}}. \end{align*} $$
$$ \begin{align*} \tau_{\chi}:=\prod_{k=0}^{d} \det(B_{\chi,k}^{2})^{k(-1)^{k+1}}. \end{align*} $$
Then, by Proposition 9.4 (see also [Reference Braverman and Kappeler5, Subsection 5.3]), for
![]() $\chi \in V$
,
$\chi \in V$
,
where
![]() $\eta (B^{\operatorname {\mathrm {even}}}_{\chi })$
denotes the eta invariant of the even part of the odd signature operator
$\eta (B^{\operatorname {\mathrm {even}}}_{\chi })$
denotes the eta invariant of the even part of the odd signature operator
![]() $B_{\chi }$
.
$B_{\chi }$
.
Let now X be an oriented, compact, hyperbolic, odd-dimensional manifold
![]() $X=\Gamma \backslash {\mathbb {H}}^{d}$
as above. By the determinant formula in [Reference Spilioti49], we obtain the following theorem.
$X=\Gamma \backslash {\mathbb {H}}^{d}$
as above. By the determinant formula in [Reference Spilioti49], we obtain the following theorem.
Theorem 1 (Theorem 9.3)
Let
![]() $\chi $
be a finite-dimensional complex representation of
$\chi $
be a finite-dimensional complex representation of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\Delta ^{\sharp }_{\chi ,k}$
be the flat Hodge Laplacian, acting on the space of k-differential forms on X with values in the flat vector bundle
$\Delta ^{\sharp }_{\chi ,k}$
be the flat Hodge Laplacian, acting on the space of k-differential forms on X with values in the flat vector bundle
![]() $E_{\chi }$
. Then, the Ruelle zeta function has the representation
$E_{\chi }$
. Then, the Ruelle zeta function has the representation
 $$ \begin{align*} R(s;\chi)=\notag&\prod_{k=0}^{d-1}\prod_{p=k}^{d-1}{{\det}_{\operatorname{\mathrm{gr}}}\big(\Delta^{\sharp}_{\chi,k}+s(s+2(\vert\rho\vert-p))\big)}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg), \end{align*} $$
$$ \begin{align*} R(s;\chi)=\notag&\prod_{k=0}^{d-1}\prod_{p=k}^{d-1}{{\det}_{\operatorname{\mathrm{gr}}}\big(\Delta^{\sharp}_{\chi,k}+s(s+2(\vert\rho\vert-p))\big)}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg), \end{align*} $$
where
![]() $\operatorname {\mathrm {Vol}}(S^{d})$
denotes the volume of the d-dimensional Euclidean unit sphere. Let
$\operatorname {\mathrm {Vol}}(S^{d})$
denotes the volume of the d-dimensional Euclidean unit sphere. Let
![]() $d_{\chi ,k}:=\dim \operatorname {\mathrm {Ker}}(\Delta _{\chi ,k})$
. Then, the singularity of the Ruelle zeta function at
$d_{\chi ,k}:=\dim \operatorname {\mathrm {Ker}}(\Delta _{\chi ,k})$
. Then, the singularity of the Ruelle zeta function at
![]() $s=0$
is of order
$s=0$
is of order
 $$ \begin{align*} \sum_{k=0}^{(d-1)/2}(d+1-2k)(-1)^{k}d_{\chi,k}. \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{(d-1)/2}(d+1-2k)(-1)^{k}d_{\chi,k}. \end{align*} $$
Let
![]() $V \subset \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
be an open neighbourhood (in classical topology) of the set
$V \subset \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
be an open neighbourhood (in classical topology) of the set
![]() $\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
of acyclic, unitary representations such that, for all
$\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
of acyclic, unitary representations such that, for all
![]() $\chi \in V$
,
$\chi \in V$
,
![]() $B_{\chi }$
is bijective. Then, for
$B_{\chi }$
is bijective. Then, for
![]() $\chi \in V$
, we obtain the following result.
$\chi \in V$
, we obtain the following result.
Theorem 2 (Theorem 10.1)
Let
![]() $\chi \in V$
. Then, the Ruelle zeta function
$\chi \in V$
. Then, the Ruelle zeta function
![]() $R(s;\chi )$
is regular at
$R(s;\chi )$
is regular at
![]() $s=0$
and is equal to the complex Cappell–Miller torsion,
$s=0$
and is equal to the complex Cappell–Miller torsion,
Corollary 1 (Corollary 10.2)
Let
![]() $\chi \in V$
. Then, the Ruelle zeta function
$\chi \in V$
. Then, the Ruelle zeta function
![]() $R(s;\chi )$
is regular at
$R(s;\chi )$
is regular at
![]() $s=0$
and is related to the refined analytic torsion
$s=0$
and is related to the refined analytic torsion
![]() $T_{\chi }$
by
$T_{\chi }$
by
We mention here the work of Müller in [Reference Müller37], where the behaviour at the origin of the twisted Ruelle zeta function associated with an arbitrary nonunitary representation is treated and the relation to the Cappell–Miller torsion. Also, Shen in [Reference Shen47] studied the relation between the Cappell–Miller torsion and the value at the zero point of the Ruelle dynamical zeta function associated to a flat vector bundle, which is not necessarily unitarily flat, on a closed odd-dimensional locally symmetric space of reductive type.
Organization of the paper
This paper is organised as follows. In Section 2, we provide the definition of the eta invariant and the regularized determinant of a non-self-adjoint elliptic differential operator. In Section 3, we introduce the odd signature operator and consider representations of the fundamental group, which are nonunitary, but closed enough, in classical topology, to acyclic and unitary representations. In Sections 4 and 5, we consider the refined analytic torsion, as it is introduced in [Reference Braverman and Kappeler6]. In Section 6, we consider the Cappell–Miller torsion, as it is introduced in [Reference Cappell and Miller8], and its relation to the refined analytic torsion. In Section 7, we summarize basic facts about hyperbolic manifolds and representations of the involved Lie groups. We define also the twisted Selberg and Ruelle zeta functions. In Section 8, we recall the definition of the twisted Laplace operator from [Reference Müller35] and certain auxiliary operators, first introduced in [Reference Bunke and Olbrich7]. In Section 9, we use the determinant formula from [Reference Spilioti49] to express the twisted Ruelle zeta function in terms of products of graded regularized determinants of twisted Hodge Laplacians on vector bundle-valued differential forms. This formula is the keypoint to study the singularity of the twisted Ruelle zeta function at
![]() $s=0$
. Finally, in Section 10, we prove the main results: Theorem 2 and Corollary 1. We include also an appendix, in Section 10, where we recall the general definition of the refined analytic torsion as an element of the determinant line from [Reference Braverman and Kappeler4].
$s=0$
. Finally, in Section 10, we prove the main results: Theorem 2 and Corollary 1. We include also an appendix, in Section 10, where we recall the general definition of the refined analytic torsion as an element of the determinant line from [Reference Braverman and Kappeler4].
2 Preliminaries on the eta invariant of a non-self-adjoint operator and graded regularized determinants
2.1 Eta invariant of an elliptic operator
Let
![]() $E\rightarrow X $
be a complex vector bundle over a smooth, compact, Riemannian manifold X of dimension d. Let
$E\rightarrow X $
be a complex vector bundle over a smooth, compact, Riemannian manifold X of dimension d. Let
![]() $D\colon C^{\infty }(X, E)\rightarrow C^{\infty }(X, E)$
be an elliptic differential operator of order
$D\colon C^{\infty }(X, E)\rightarrow C^{\infty }(X, E)$
be an elliptic differential operator of order
![]() $m\geq 1$
. Let
$m\geq 1$
. Let
![]() $\sigma (D)$
be its principal symbol.
$\sigma (D)$
be its principal symbol.
Definition 2.1.1. Let
![]() $R_{\theta }:=\{\rho e^ {i\theta }: \rho \in [0,\infty ]\}$
. The angle
$R_{\theta }:=\{\rho e^ {i\theta }: \rho \in [0,\infty ]\}$
. The angle
![]() $\theta \in [0,2\pi )$
is a principal angle for D if
$\theta \in [0,2\pi )$
is a principal angle for D if
Definition 2.1.2. Let
![]() $I\subset [0,2\pi )$
. Let
$I\subset [0,2\pi )$
. Let
![]() $L_{I}$
be a solid angle defined by
$L_{I}$
be a solid angle defined by
The angle
![]() $\theta $
is an Agmon angle for D if it is a principal angle for D and there exists an
$\theta $
is an Agmon angle for D if it is a principal angle for D and there exists an
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
We define here the eta function associated with non-self-adjoint operators D with elliptic, self-adjoint principal symbol (see [Reference Gilkey21]). By [Reference Markus26, §I.6], the space
![]() $L^{2}(X,E)$
of square integrable sections of E is the closure of the algebraic direct sum of finite-dimensional D-invariant subspaces
$L^{2}(X,E)$
of square integrable sections of E is the closure of the algebraic direct sum of finite-dimensional D-invariant subspaces
 $$ \begin{align*} L^{2}(X,E)=\overline{\bigoplus\limits_{k\geq 1} \Lambda_{k}} \end{align*} $$
$$ \begin{align*} L^{2}(X,E)=\overline{\bigoplus\limits_{k\geq 1} \Lambda_{k}} \end{align*} $$
such that the restriction of D to
![]() $\Lambda _{k}$
has a unique eigenvalue
$\Lambda _{k}$
has a unique eigenvalue
![]() $\lambda _{k}$
and
$\lambda _{k}$
and
![]() $\lim _{k\rightarrow \infty }\vert \lambda _{k}\vert =\infty $
. In general, the above sum is not a sum of mutually orthogonal subspaces. The space
$\lim _{k\rightarrow \infty }\vert \lambda _{k}\vert =\infty $
. In general, the above sum is not a sum of mutually orthogonal subspaces. The space
![]() $\Lambda _{k}$
is called the space of root vectors of D with eigenvalue
$\Lambda _{k}$
is called the space of root vectors of D with eigenvalue
![]() $\lambda _{k}$
. The algebraic multiplicity
$\lambda _{k}$
. The algebraic multiplicity
![]() $m_{k}$
of the eigenvalue
$m_{k}$
of the eigenvalue
![]() $\lambda _{k}$
is defined as the dimension of the space
$\lambda _{k}$
is defined as the dimension of the space
![]() $\Lambda _{k}$
. Since the principal symbol of D is self-adjoint, the angles
$\Lambda _{k}$
. Since the principal symbol of D is self-adjoint, the angles
![]() $\pm \pi /2$
are principal angles for D. Hence, D also possesses an Agmon angle (see [Reference Braverman and Kappeler6, Section 3.10]). Let
$\pm \pi /2$
are principal angles for D. Hence, D also possesses an Agmon angle (see [Reference Braverman and Kappeler6, Section 3.10]). Let
![]() $\theta $
be an Agmon angle for D. Denote by
$\theta $
be an Agmon angle for D. Denote by
![]() $\log _{\theta }\lambda _{k}$
the branch of the logarithm in
$\log _{\theta }\lambda _{k}$
the branch of the logarithm in
![]() $\mathbb {C}\setminus R_{\theta }$
with
$\mathbb {C}\setminus R_{\theta }$
with
![]() $\theta <\operatorname {\mathrm {Im}}(\log _{\theta }\lambda _{k})<\theta +2\pi $
. Let
$\theta <\operatorname {\mathrm {Im}}(\log _{\theta }\lambda _{k})<\theta +2\pi $
. Let
![]() $(\lambda _{k})_{\theta }:=e^{\log _{\theta }\lambda _{k}}$
.
$(\lambda _{k})_{\theta }:=e^{\log _{\theta }\lambda _{k}}$
.
Definition 2.1.3. For Re
![]() $(s)\gg 0$
, we define the eta function
$(s)\gg 0$
, we define the eta function
![]() $\eta _{\theta }(s,D)$
of D by
$\eta _{\theta }(s,D)$
of D by
 $$ \begin{align*} \eta_{\theta}(s,D):=\sum_{\text{{Re}}(\lambda_{k})>0} m_{k}(\lambda_{k})_{\theta}^{-s}-\sum_{\text{{Re}}(\lambda_{k})<0} m_{k}(-\lambda_{k})_{\theta}^{-s}. \end{align*} $$
$$ \begin{align*} \eta_{\theta}(s,D):=\sum_{\text{{Re}}(\lambda_{k})>0} m_{k}(\lambda_{k})_{\theta}^{-s}-\sum_{\text{{Re}}(\lambda_{k})<0} m_{k}(-\lambda_{k})_{\theta}^{-s}. \end{align*} $$
Note that since the angles
![]() $\pm \pi /2$
are principal angles for D, there are at most finitely many eigenvalues of D on or near the imaginary axis. Hence, the eigenvalues of D that are purely imaginary do not contribute to the definition of the eta function. It has been shown by Grubb and Seeley ([Reference Grubb and Seeley23, Theorem 2.7]) that
$\pm \pi /2$
are principal angles for D, there are at most finitely many eigenvalues of D on or near the imaginary axis. Hence, the eigenvalues of D that are purely imaginary do not contribute to the definition of the eta function. It has been shown by Grubb and Seeley ([Reference Grubb and Seeley23, Theorem 2.7]) that
![]() $\eta _{\theta }(s,D)$
has a meromorphic continuation to the whole complex plane
$\eta _{\theta }(s,D)$
has a meromorphic continuation to the whole complex plane
![]() $\mathbb {C}$
with isolated simple poles and that is regular at
$\mathbb {C}$
with isolated simple poles and that is regular at
![]() $s=0$
. Moreover, the number
$s=0$
. Moreover, the number
![]() $\eta _{\theta }(0,D)$
is independent of the Agmon angle
$\eta _{\theta }(0,D)$
is independent of the Agmon angle
![]() $\theta $
. Hence, we write
$\theta $
. Hence, we write
![]() $\eta (0,D)$
instead of
$\eta (0,D)$
instead of
![]() $\eta _{\theta }(0,D)$
.
$\eta _{\theta }(0,D)$
.
Definition 2.1.4. Let
![]() $m_{+}$
, respectively
$m_{+}$
, respectively
![]() $m_{-}$
, denote the number of the eigenvalues of D on the positive, respectively negative, part of the imaginary axis. We define the eta invariant
$m_{-}$
, denote the number of the eigenvalues of D on the positive, respectively negative, part of the imaginary axis. We define the eta invariant
![]() $\eta (D)$
of the operator D by
$\eta (D)$
of the operator D by
By [Reference Braverman and Kappeler6, (3.25)],
![]() $\eta (D)$
is independent of the Agmon angle
$\eta (D)$
is independent of the Agmon angle
![]() $\theta $
.
$\theta $
.
2.2 Regularized determinant of an elliptic operator
We recall here the definition of the regularized determinant of an elliptic operator. For more details, we refer the reader to [Reference Braverman and Kappeler6, Subsection 3.5 and Definition 3.6]. Let
![]() $X,E$
and D be as in the previous subsection. We assume, in addition, that D has a self-adjoint principal symbol and it is invertible. Let
$X,E$
and D be as in the previous subsection. We assume, in addition, that D has a self-adjoint principal symbol and it is invertible. Let
![]() $\theta $
be an Agmon angle for D. We define the zeta function
$\theta $
be an Agmon angle for D. We define the zeta function
![]() $\zeta _{\theta }(s,D)$
by
$\zeta _{\theta }(s,D)$
by
where
![]() $D_{\theta }^{-s}$
is a pseudodifferential operator with continuous kernel (see [Reference Braverman and Kappeler6, (3.15)]). The zeta function
$D_{\theta }^{-s}$
is a pseudodifferential operator with continuous kernel (see [Reference Braverman and Kappeler6, (3.15)]). The zeta function
![]() $\zeta _{\theta }(s,D)$
admits a meromorphic continuation to
$\zeta _{\theta }(s,D)$
admits a meromorphic continuation to
![]() $\mathbb {C}$
, and it is regular at zero ([Reference Seeley45]). We define the regularized determinant of D by
$\mathbb {C}$
, and it is regular at zero ([Reference Seeley45]). We define the regularized determinant of D by
 $$ \begin{align*} {\det}_{\theta}:=\exp\bigg( -\frac{d}{ds}\bigg\vert_{s=0} \zeta_{\theta}(s,D) \bigg). \end{align*} $$
$$ \begin{align*} {\det}_{\theta}:=\exp\bigg( -\frac{d}{ds}\bigg\vert_{s=0} \zeta_{\theta}(s,D) \bigg). \end{align*} $$
We denote by
![]() $L{\det }_{\theta }$
the particular value of the logarithm of the determinant such that
$L{\det }_{\theta }$
the particular value of the logarithm of the determinant such that
By [Reference Braverman and Kappeler6, Subsection 3.10], the regularized determinant
![]() ${\det }_{\theta }(D)$
is independent of the Agmon angle
${\det }_{\theta }(D)$
is independent of the Agmon angle
![]() $\theta $
.
$\theta $
.
2.3 Graded regularized determinant of an elliptic operator
We recall here the notion of the graded regularized determinant of an elliptic differential operator. Let
![]() $E=E_{+}\oplus E_{-}$
be a
$E=E_{+}\oplus E_{-}$
be a
![]() $\mathbb {Z}_{2}$
-graded vector bundle over a compact, Riemannian manifold X. Let
$\mathbb {Z}_{2}$
-graded vector bundle over a compact, Riemannian manifold X. Let
![]() $D\colon C^{\infty }(X,E)\rightarrow C^{\infty }(X,E)$
be an elliptic differential operator, which is bounded from below. We assume that D preserves the grading, that is, we assume that with respect to the decomposition
$D\colon C^{\infty }(X,E)\rightarrow C^{\infty }(X,E)$
be an elliptic differential operator, which is bounded from below. We assume that D preserves the grading, that is, we assume that with respect to the decomposition
D takes the form,
 $$ \begin{align*} D= \left( {\begin{array}{@{}cc@{}} D{+} & 0 \\ 0 & D_{-} \\ \end{array} } \right). \end{align*} $$
$$ \begin{align*} D= \left( {\begin{array}{@{}cc@{}} D{+} & 0 \\ 0 & D_{-} \\ \end{array} } \right). \end{align*} $$
Then, the graded determinant
![]() $\det _{\operatorname {\mathrm {gr}}}(D)$
of D is defined by
$\det _{\operatorname {\mathrm {gr}}}(D)$
of D is defined by
 $$ \begin{align*} {\det}_{\operatorname{\mathrm{gr}}}(D)=\frac{\det(D_{+})}{\det(D_{-})}, \end{align*} $$
$$ \begin{align*} {\det}_{\operatorname{\mathrm{gr}}}(D)=\frac{\det(D_{+})}{\det(D_{-})}, \end{align*} $$
where
![]() $\det (D_{+})$
and
$\det (D_{+})$
and
![]() $ \det (D_{-})$
denote the regularized determinants of the operators
$ \det (D_{-})$
denote the regularized determinants of the operators
![]() $D_{+}$
and
$D_{+}$
and
![]() $D_{-}$
, respectively.
$D_{-}$
, respectively.
3 Spaces of representations of the fundamental group
3.1 Odd signature operator
Following the idea of Braverman and Kappeler in [Reference Braverman and Kappeler6], we consider representations of
![]() $\Gamma $
, which are nonunitary, but belong to a neighbourhood of the set of acyclic, unitary representations in a suitable topology such that the odd signature operator B (see Definition 3.1.1 below) is bijective. For these representations, Braverman and Kappeler defined the refined analytic torsion for a compact, oriented, odd-dimensional manifold X. Having applications in mind, instead of considering the regularized determinant of the (flat) Laplacian they consider the graded determinant of the even part of its square root, the odd signature operator B. We recall here some definitions from [Reference Braverman and Kappeler6].
$\Gamma $
, which are nonunitary, but belong to a neighbourhood of the set of acyclic, unitary representations in a suitable topology such that the odd signature operator B (see Definition 3.1.1 below) is bijective. For these representations, Braverman and Kappeler defined the refined analytic torsion for a compact, oriented, odd-dimensional manifold X. Having applications in mind, instead of considering the regularized determinant of the (flat) Laplacian they consider the graded determinant of the even part of its square root, the odd signature operator B. We recall here some definitions from [Reference Braverman and Kappeler6].
Let X be a compact, oriented, Riemannian manifold of odd dimension
![]() $d=2r-1$
. Denote by g the Riemannian metric on X. Let
$d=2r-1$
. Denote by g the Riemannian metric on X. Let
![]() $E\rightarrow X$
be a complex vector bundle over X, endowed with a flat connection
$E\rightarrow X$
be a complex vector bundle over X, endowed with a flat connection
![]() $\nabla $
. Let
$\nabla $
. Let
![]() $\Lambda ^{k}(X,E)$
be the space of k-differential forms on X with values in E. We denote by
$\Lambda ^{k}(X,E)$
be the space of k-differential forms on X with values in E. We denote by
![]() $\nabla $
the induced differential
$\nabla $
the induced differential
![]() $\nabla \colon \Lambda ^{k}(X,E)\rightarrow \Lambda ^{k+1}(X,E)$
. Let
$\nabla \colon \Lambda ^{k}(X,E)\rightarrow \Lambda ^{k+1}(X,E)$
. Let
![]() $\Gamma \colon \Lambda ^{k}(X,E) \rightarrow \Lambda ^{d-k}(X,E)$
be the chirality operator defined by the formula
$\Gamma \colon \Lambda ^{k}(X,E) \rightarrow \Lambda ^{d-k}(X,E)$
be the chirality operator defined by the formula
where
![]() $\ast '$
denotes the operator acting on sections of
$\ast '$
denotes the operator acting on sections of
![]() $\Lambda ^{k}T^{\ast }X\otimes E$
as
$\Lambda ^{k}T^{\ast }X\otimes E$
as
![]() $\ast \otimes \operatorname {\mathrm {Id}}$
, and
$\ast \otimes \operatorname {\mathrm {Id}}$
, and
![]() $\ast $
is the usual Hodge
$\ast $
is the usual Hodge
![]() $\ast $
-operator.
$\ast $
-operator.
Definition 3.1.1. We define the odd signature operator
![]() $B=B(\nabla , g)$
acting on
$B=B(\nabla , g)$
acting on
![]() $\Lambda ^{*}(X,E)$
by
$\Lambda ^{*}(X,E)$
by
We set
 $$ \begin{align*} \Lambda^{\operatorname{\mathrm{even}}}(X,E):=\bigoplus_{p=0}^{r-1} \Lambda^{2p}(X,E). \end{align*} $$
$$ \begin{align*} \Lambda^{\operatorname{\mathrm{even}}}(X,E):=\bigoplus_{p=0}^{r-1} \Lambda^{2p}(X,E). \end{align*} $$
Let
![]() $B^{\operatorname {\mathrm {even}}}$
be the even part of the odd signature operator B, defined by
$B^{\operatorname {\mathrm {even}}}$
be the even part of the odd signature operator B, defined by
![]() $B^{\operatorname {\mathrm {even}}}:=B\colon \Lambda ^{\operatorname {\mathrm {even}}}(X,E)\rightarrow \Lambda ^{\operatorname {\mathrm {even}}}(X,E)$
.
$B^{\operatorname {\mathrm {even}}}:=B\colon \Lambda ^{\operatorname {\mathrm {even}}}(X,E)\rightarrow \Lambda ^{\operatorname {\mathrm {even}}}(X,E)$
.
3.2 Spaces of connections
We consider the following two assumptions.
Assumption 1. The connection
![]() $\nabla $
is acyclic, that is, the twisted de Rham complex
$\nabla $
is acyclic, that is, the twisted de Rham complex
is acyclic,
for every
![]() $k=1,\ldots ,d$
.
$k=1,\ldots ,d$
.
Assumption 2. The odd signature operator
![]() $B\colon \Lambda ^{k}(X,E)\rightarrow \Lambda ^{k}(X,E)$
is bijective.
$B\colon \Lambda ^{k}(X,E)\rightarrow \Lambda ^{k}(X,E)$
is bijective.
Suppose that there exists a Hermitian metric h on E, which is preserved by
![]() $\nabla $
. In such a case, we call
$\nabla $
. In such a case, we call
![]() $\nabla $
a Hermitian connection. For such connections, one can easily see that Assumption 1 implies Assumption 2 and vice versa (see [Reference Braverman and Kappeler6, Subsection 6.6]). Hence, all acyclic, Hermitian connections satisfy Assumptions 1 and 2.
$\nabla $
a Hermitian connection. For such connections, one can easily see that Assumption 1 implies Assumption 2 and vice versa (see [Reference Braverman and Kappeler6, Subsection 6.6]). Hence, all acyclic, Hermitian connections satisfy Assumptions 1 and 2.
Following [Reference Braverman and Kappeler6], we denote by
![]() $\Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
the space of
$\Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
the space of
![]() $1$
-forms with values in
$1$
-forms with values in
![]() $\operatorname {\mathrm {End}}(E)$
. We define the sup-norm on
$\operatorname {\mathrm {End}}(E)$
. We define the sup-norm on
![]() $\Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
by
$\Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
by
where the norm
![]() $\lvert \cdot \rvert $
is induced by a Hermitian metric on E and a Riemannian metric on X. The topology defined by this norm is called the
$\lvert \cdot \rvert $
is induced by a Hermitian metric on E and a Riemannian metric on X. The topology defined by this norm is called the
![]() $C^{0}$
-topology and it is independent of the metrics. We identify the space of connections on E with
$C^{0}$
-topology and it is independent of the metrics. We identify the space of connections on E with
![]() $\Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
by choosing a connection
$\Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
by choosing a connection
![]() $\nabla _{0}$
and associating to a connection
$\nabla _{0}$
and associating to a connection
![]() $\nabla $
the
$\nabla $
the
![]() $1$
-form
$1$
-form
![]() $\nabla -\nabla _{0}\in \Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
. Hence, by this identification, the
$\nabla -\nabla _{0}\in \Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
. Hence, by this identification, the
![]() $C^{0}$
-topology on
$C^{0}$
-topology on
![]() $\Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
provides a topology on the space of connections on E, which is independent of the choice of
$\Lambda ^{1}(X,\operatorname {\mathrm {End}}(E))$
provides a topology on the space of connections on E, which is independent of the choice of
![]() $\nabla _{0}$
. This topology is called the
$\nabla _{0}$
. This topology is called the
![]() $C^{0}$
-topology on the space of connections.
$C^{0}$
-topology on the space of connections.
Let
![]() $\operatorname {\mathrm {Flat}}(E)$
be the set of flat connections on E and
$\operatorname {\mathrm {Flat}}(E)$
be the set of flat connections on E and
![]() $\operatorname {\mathrm {Flat}}'(E,g)\subset \operatorname {\mathrm {Flat}}(E)$
be the set of flat connections on E, satisfying Assumptions 1 and 2. The topology induced on these sets by the
$\operatorname {\mathrm {Flat}}'(E,g)\subset \operatorname {\mathrm {Flat}}(E)$
be the set of flat connections on E, satisfying Assumptions 1 and 2. The topology induced on these sets by the
![]() $C^{0}$
-topology on the space of connections on E is also called the
$C^{0}$
-topology on the space of connections on E is also called the
![]() $C^{0}$
-topology. The following proposition is proved in [Reference Braverman and Kappeler6].
$C^{0}$
-topology. The following proposition is proved in [Reference Braverman and Kappeler6].
Proposition 3.2.1.
![]() $\operatorname {\mathrm {Flat}}'(E,g)$
is an
$\operatorname {\mathrm {Flat}}'(E,g)$
is an
![]() $C^{0}$
-open subset of
$C^{0}$
-open subset of
![]() $\operatorname {\mathrm {Flat}}(E)$
, which contains all acyclic Hermitian connections on E.
$\operatorname {\mathrm {Flat}}(E)$
, which contains all acyclic Hermitian connections on E.
Proof. See [Reference Braverman and Kappeler6, Proposition 6.8].
3.3 Spaces of representations
Let
![]() $\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
be the space of all n-dimensional, complex representations of
$\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
be the space of all n-dimensional, complex representations of
![]() $\pi _{1}(X)$
. This space has a natural structure of a complex algebraic variety. Let
$\pi _{1}(X)$
. This space has a natural structure of a complex algebraic variety. Let
![]() $\{\gamma _{1},\ldots ,\gamma _{L}\}$
be a finite set of generators of
$\{\gamma _{1},\ldots ,\gamma _{L}\}$
be a finite set of generators of
![]() $\pi _{1}(X)$
. The elements
$\pi _{1}(X)$
. The elements
![]() $\gamma _{i}$
satisfy finitely many relations. Then, a representation
$\gamma _{i}$
satisfy finitely many relations. Then, a representation
![]() $\chi \in \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
is given by
$\chi \in \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
is given by
![]() $2L$
invertible
$2L$
invertible
![]() $n\times n$
-matrices
$n\times n$
-matrices
![]() $\chi (\gamma _{1}),\ldots ,\chi (\gamma _{L}),\chi (\gamma _{1}^{-1}),\ldots ,\chi (\gamma _{L}^{-1})$
, which satisfy finitely many polynomial equations. Hence, we view
$\chi (\gamma _{1}),\ldots ,\chi (\gamma _{L}),\chi (\gamma _{1}^{-1}),\ldots ,\chi (\gamma _{L}^{-1})$
, which satisfy finitely many polynomial equations. Hence, we view
![]() $\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
as an algebraic subset of
$\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
as an algebraic subset of
![]() $\operatorname {\mathrm {Mat}}_{n\times n}(\mathbb {C})^{2L}$
with the induced topology.
$\operatorname {\mathrm {Mat}}_{n\times n}(\mathbb {C})^{2L}$
with the induced topology.
For a representation
![]() $\chi \in \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
, we consider the associated flat vector bundle
$\chi \in \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
, we consider the associated flat vector bundle
![]() $E_{\chi }\rightarrow X$
. Let
$E_{\chi }\rightarrow X$
. Let
![]() $\nabla _{\chi }$
be the flat connection on
$\nabla _{\chi }$
be the flat connection on
![]() $E_{\chi }$
. Then, the monodromy of
$E_{\chi }$
. Then, the monodromy of
![]() $\nabla _{\chi }$
is isomorphic to
$\nabla _{\chi }$
is isomorphic to
![]() $\chi $
. We denote also by
$\chi $
. We denote also by
![]() $\nabla _{\chi }$
the induced differential
$\nabla _{\chi }$
the induced differential
![]() $\nabla _{\chi }\colon \Lambda ^{*}(X,E_{\chi })\rightarrow \Lambda ^{*+1}(X,E_{\chi })$
. We denote by
$\nabla _{\chi }\colon \Lambda ^{*}(X,E_{\chi })\rightarrow \Lambda ^{*+1}(X,E_{\chi })$
. We denote by
![]() $B_{\chi }$
the odd signature operator
$B_{\chi }$
the odd signature operator
![]() $B_{\chi }=B(\nabla _{\chi },g)$
acting on
$B_{\chi }=B(\nabla _{\chi },g)$
acting on
![]() $\Lambda ^{*}(X,E_{\chi })$
. Let
$\Lambda ^{*}(X,E_{\chi })$
. Let
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
be the restriction of
$B_{\chi }^{\operatorname {\mathrm {even}}}$
be the restriction of
![]() $B_{\chi }$
to
$B_{\chi }$
to
![]() $\Lambda ^{\operatorname {\mathrm {even}}}(X,E_{\chi })$
.
$\Lambda ^{\operatorname {\mathrm {even}}}(X,E_{\chi })$
.
Let
![]() $\operatorname {\mathrm {Rep}}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all acyclic representations of
$\operatorname {\mathrm {Rep}}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all acyclic representations of
![]() $\pi _{1}(X)$
, that is, the set of all representations
$\pi _{1}(X)$
, that is, the set of all representations
![]() $\chi $
such that
$\chi $
such that
![]() $\nabla _{\chi }$
is acyclic. Let
$\nabla _{\chi }$
is acyclic. Let
![]() $\operatorname {\mathrm {Rep}}^{u}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all unitary representations of
$\operatorname {\mathrm {Rep}}^{u}(\pi _{1}(X),\mathbb {C}^{n})$
be the set of all unitary representations of
![]() $\pi _{1}(X)$
, that is, the set of all representations
$\pi _{1}(X)$
, that is, the set of all representations
![]() $\chi $
such that there exists a Hermitian scalar product
$\chi $
such that there exists a Hermitian scalar product
![]() $(\cdot ,\cdot )$
on
$(\cdot ,\cdot )$
on
![]() $\mathbb {C}^{n}$
, which is preserved by the matrices
$\mathbb {C}^{n}$
, which is preserved by the matrices
![]() $\chi (\gamma )$
, for all
$\chi (\gamma )$
, for all
![]() $\gamma \in \pi _{1}(X)$
.
$\gamma \in \pi _{1}(X)$
.
![]() $\operatorname {\mathrm {Rep}}^{u}(\pi _{1}(X),\mathbb {C}^{n})$
can be viewed as the real locus of the complex algebraic variety
$\operatorname {\mathrm {Rep}}^{u}(\pi _{1}(X),\mathbb {C}^{n})$
can be viewed as the real locus of the complex algebraic variety
![]() $\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
. We set
$\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
. We set
Suppose that for some representation
![]() $\chi _{0}\in \operatorname {\mathrm {Rep}}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
the operator
$\chi _{0}\in \operatorname {\mathrm {Rep}}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
the operator
![]() $B_{\chi _{0}}$
is bijective. Then, there exists an open neighbourhood (in classical topology)
$B_{\chi _{0}}$
is bijective. Then, there exists an open neighbourhood (in classical topology)
![]() $V \subset \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
of the set
$V \subset \operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
of the set
![]() $\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
of acyclic, unitary representations such that, for all
$\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
of acyclic, unitary representations such that, for all
![]() $\chi \in V$
, the pair
$\chi \in V$
, the pair
![]() $(\nabla _{\chi },g)$
satisfies Assumptions 1 and 2 of Subsection 6.2 (see [Reference Braverman and Kappeler6, Subsection 13.7]).
$(\nabla _{\chi },g)$
satisfies Assumptions 1 and 2 of Subsection 6.2 (see [Reference Braverman and Kappeler6, Subsection 13.7]).
4 Refined analytic torsion
4.1 Definition
Let
![]() $\nabla $
be acyclic. Let
$\nabla $
be acyclic. Let
![]() $\cal {M}(\nabla )$
be the set of all Riemannian metrics g on X such that
$\cal {M}(\nabla )$
be the set of all Riemannian metrics g on X such that
![]() $B^{\operatorname {\mathrm {even}}}=B^{\operatorname {\mathrm {even}}}(\nabla ,g)$
is bijective. Then, by [Reference Braverman and Kappeler6, Proposition 6.8],
$B^{\operatorname {\mathrm {even}}}=B^{\operatorname {\mathrm {even}}}(\nabla ,g)$
is bijective. Then, by [Reference Braverman and Kappeler6, Proposition 6.8],
![]() $\cal {M}(\nabla )\neq \emptyset $
, for all flat connections in an open neighbourhood, in
$\cal {M}(\nabla )\neq \emptyset $
, for all flat connections in an open neighbourhood, in
![]() $C^{0}$
-topology, of the set of acyclic Hermitian connections. Let V be an open neighbourhood of
$C^{0}$
-topology, of the set of acyclic Hermitian connections. Let V be an open neighbourhood of
![]() $\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
as in Subsection 3.3.
$\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
as in Subsection 3.3.
Definition 4.1.1. Let
![]() $\chi \in V$
. We define the refined analytic torsion
$\chi \in V$
. We define the refined analytic torsion
![]() $T_{\chi }=T(\nabla _{\chi })$
by
$T_{\chi }=T(\nabla _{\chi })$
by
where
![]() $\eta _{\operatorname {\mathrm {tr}}}=\eta _{tr}(g)=\frac {1}{2}\eta (0, B_{tr}(g))$
, and
$\eta _{\operatorname {\mathrm {tr}}}=\eta _{tr}(g)=\frac {1}{2}\eta (0, B_{tr}(g))$
, and
![]() $\eta (0, B_{tr}(g))$
denotes the eta invariant of the even part of the odd signature operator corresponding to the trivial line bundle, endowed with the trivial connection. The refined analytic torsion is independent of the Agmon angle
$\eta (0, B_{tr}(g))$
denotes the eta invariant of the even part of the odd signature operator corresponding to the trivial line bundle, endowed with the trivial connection. The refined analytic torsion is independent of the Agmon angle
![]() $\theta \in (-\pi ,0)$
for the operator
$\theta \in (-\pi ,0)$
for the operator
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}=B_{\chi }^{\operatorname {\mathrm {even}}}(g)$
and the Riemannian metric
$B_{\chi }^{\operatorname {\mathrm {even}}}=B_{\chi }^{\operatorname {\mathrm {even}}}(g)$
and the Riemannian metric
![]() $g\in \cal {M}(\nabla )$
.
$g\in \cal {M}(\nabla )$
.
Remark 4.1.2. The graded determinant of the operator
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
is slightly different than the usual expression of the graded determinant as in Subsection 2.2.3. We recall here briefly the definition of
$B_{\chi }^{\operatorname {\mathrm {even}}}$
is slightly different than the usual expression of the graded determinant as in Subsection 2.2.3. We recall here briefly the definition of
![]() ${\det }_{\operatorname {\mathrm {gr}}}(B_{\chi }^{\operatorname {\mathrm {even}}})$
. For more details, we refer the reader to [Reference Braverman and Kappeler6, Subsection 2.2 and 6.11]. We set
${\det }_{\operatorname {\mathrm {gr}}}(B_{\chi }^{\operatorname {\mathrm {even}}})$
. For more details, we refer the reader to [Reference Braverman and Kappeler6, Subsection 2.2 and 6.11]. We set
 $$ \begin{align*} &\Lambda^{k}_{+}(X,E):=\operatorname{\mathrm{Ker}}(\nabla\Gamma)\cap\Lambda^{k}(X,E)\\ &\Lambda^{k}_{-}(X,E):=\operatorname{\mathrm{Ker}}(\Gamma\nabla)\cap\Lambda^{k}(X,E). \end{align*} $$
$$ \begin{align*} &\Lambda^{k}_{+}(X,E):=\operatorname{\mathrm{Ker}}(\nabla\Gamma)\cap\Lambda^{k}(X,E)\\ &\Lambda^{k}_{-}(X,E):=\operatorname{\mathrm{Ker}}(\Gamma\nabla)\cap\Lambda^{k}(X,E). \end{align*} $$
Assumption 2 in Subsection 3.2 implies that
![]() $\Lambda ^{k}(X,E)=\Lambda ^{k}_{+}(X,E)\oplus \Lambda ^{k}_{-}(X,E)$
(see [Reference Braverman and Kappeler6, Subsection 6.9]). We set
$\Lambda ^{k}(X,E)=\Lambda ^{k}_{+}(X,E)\oplus \Lambda ^{k}_{-}(X,E)$
(see [Reference Braverman and Kappeler6, Subsection 6.9]). We set
 $$ \begin{align*} \Lambda^{\operatorname{\mathrm{even}}}_{\pm}(X,E)=\bigoplus_{p=0}^{r-1} \Lambda^{2p}_{\pm}(X,E). \end{align*} $$
$$ \begin{align*} \Lambda^{\operatorname{\mathrm{even}}}_{\pm}(X,E)=\bigoplus_{p=0}^{r-1} \Lambda^{2p}_{\pm}(X,E). \end{align*} $$
We denote by
![]() $B_{\chi ,\pm }^{\operatorname {\mathrm {even}}}$
the restriction of
$B_{\chi ,\pm }^{\operatorname {\mathrm {even}}}$
the restriction of
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
to
$B_{\chi }^{\operatorname {\mathrm {even}}}$
to
![]() $\Lambda ^{\operatorname {\mathrm {even}}}_{\pm }(X,E)$
. Then,
$\Lambda ^{\operatorname {\mathrm {even}}}_{\pm }(X,E)$
. Then,
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
leaves the subspaces
$B_{\chi }^{\operatorname {\mathrm {even}}}$
leaves the subspaces
![]() $\Lambda ^{\operatorname {\mathrm {even}}}_{\pm }(X,E)$
invariant. By Assumption 2, the operators
$\Lambda ^{\operatorname {\mathrm {even}}}_{\pm }(X,E)$
invariant. By Assumption 2, the operators
![]() $B_{\chi ,\pm }^{\operatorname {\mathrm {even}}}$
are bijective. Hence, we define the graded determinant
$B_{\chi ,\pm }^{\operatorname {\mathrm {even}}}$
are bijective. Hence, we define the graded determinant
![]() ${\det }_{\operatorname {\mathrm {gr}}}(B_{\chi }^{\operatorname {\mathrm {even}}})\in \mathbb {C} \backslash \{0\}$
of
${\det }_{\operatorname {\mathrm {gr}}}(B_{\chi }^{\operatorname {\mathrm {even}}})\in \mathbb {C} \backslash \{0\}$
of
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
by
$B_{\chi }^{\operatorname {\mathrm {even}}}$
by
 $$ \begin{align*} {\det}_{\operatorname{\mathrm{gr}},\theta}(B_{\chi}^{\operatorname{\mathrm{even}}}):=\frac{\det_{\theta}(B_{\chi,+}^{\operatorname{\mathrm{even}}})} {\det_{\theta}(-B_{\chi,-}^{\operatorname{\mathrm{even}}})}, \end{align*} $$
$$ \begin{align*} {\det}_{\operatorname{\mathrm{gr}},\theta}(B_{\chi}^{\operatorname{\mathrm{even}}}):=\frac{\det_{\theta}(B_{\chi,+}^{\operatorname{\mathrm{even}}})} {\det_{\theta}(-B_{\chi,-}^{\operatorname{\mathrm{even}}})}, \end{align*} $$
where
![]() $\theta $
is an Agmon angle for
$\theta $
is an Agmon angle for
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
(and an Agmon angle for
$B_{\chi }^{\operatorname {\mathrm {even}}}$
(and an Agmon angle for
![]() $B_{\chi ,\pm }^{\operatorname {\mathrm {even}}}$
as well).
$B_{\chi ,\pm }^{\operatorname {\mathrm {even}}}$
as well).
Remark 4.1.3. By [Reference Braverman and Kappeler6, Corollary 13.11.(2)], the refined analytic torsion
![]() $T_{\chi }$
is an holomorphic function on the set
$T_{\chi }$
is an holomorphic function on the set
![]() $V\backslash \Sigma $
, where
$V\backslash \Sigma $
, where
![]() $\Sigma $
denotes the set of singular points of the complex algebraic variety
$\Sigma $
denotes the set of singular points of the complex algebraic variety
![]() $\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
.
$\operatorname {\mathrm {Rep}}(\pi _{1}(X),\mathbb {C}^{n})$
.
4.2 Independence of the refined analytic torsion of the Riemannian metric and the Agmon angle
In [Reference Braverman and Kappeler6, Theorem 9.3], it is proved that
![]() $T_{\chi }$
is independent of the Agmon angle
$T_{\chi }$
is independent of the Agmon angle
![]() $\theta $
and the Riemannian metric g. We set
$\theta $
and the Riemannian metric g. We set
 $$ \begin{align} \xi=\xi(\chi,g,\theta):=\frac{1}{2}\sum_{k=0}^{d}(-1)^{k+1}k L{\det}_{2\theta}(B_{\chi}^{2}|_{\Lambda^{k}(X,E_{\chi})}). \end{align} $$
$$ \begin{align} \xi=\xi(\chi,g,\theta):=\frac{1}{2}\sum_{k=0}^{d}(-1)^{k+1}k L{\det}_{2\theta}(B_{\chi}^{2}|_{\Lambda^{k}(X,E_{\chi})}). \end{align} $$
The number
![]() $\xi $
is defined in [Reference Braverman and Kappeler6, (7.79)] (see also (8.102) in the same paper). Let
$\xi $
is defined in [Reference Braverman and Kappeler6, (7.79)] (see also (8.102) in the same paper). Let
![]() $\eta =\eta (\chi ,g)=\eta (B^{\operatorname {\mathrm {even}}}_{\chi })$
denote the eta invariant of the even part of the odd signature operator
$\eta =\eta (\chi ,g)=\eta (B^{\operatorname {\mathrm {even}}}_{\chi })$
denote the eta invariant of the even part of the odd signature operator
![]() $B_{\chi }$
. By [Reference Braverman and Kappeler6, Theorem 7.2], for a suitable choice of an Agmon angle for
$B_{\chi }$
. By [Reference Braverman and Kappeler6, Theorem 7.2], for a suitable choice of an Agmon angle for
![]() $B_{\chi }$
, the following equality holds
$B_{\chi }$
, the following equality holds
The graded determinant
![]() ${\det }_{\operatorname {\mathrm {gr}}}(B_{\chi }^{\operatorname {\mathrm {even}}})$
above does depend on the Riemannian metric g. This is the reason why the additional exponential
${\det }_{\operatorname {\mathrm {gr}}}(B_{\chi }^{\operatorname {\mathrm {even}}})$
above does depend on the Riemannian metric g. This is the reason why the additional exponential
![]() $e^{i\pi \operatorname {\mathrm {rank}}(E_{\chi })\eta _{tr}(g)}$
is considered in the definition of the refined analytic torsion in [Reference Braverman and Kappeler6], to remove the metric anomaly. By results in [Reference Gilkey21, p. 52], modulo
$e^{i\pi \operatorname {\mathrm {rank}}(E_{\chi })\eta _{tr}(g)}$
is considered in the definition of the refined analytic torsion in [Reference Braverman and Kappeler6], to remove the metric anomaly. By results in [Reference Gilkey21, p. 52], modulo
![]() $\mathbb {Z}$
, the difference
$\mathbb {Z}$
, the difference
is independent of g. In addition, by [Reference Braverman and Kappeler6, Proposition 9.7], for
![]() $g_{1},g_{2}\in \mathcal {M}(\nabla )$
and suitable choices of Agmon angles
$g_{1},g_{2}\in \mathcal {M}(\nabla )$
and suitable choices of Agmon angles
![]() $\theta _{0},\theta _{1}$
,
$\theta _{0},\theta _{1}$
,
Hence, for different choices of Agmon angles and Riemannian metrics, the corresponding expressions in Equation (4.1) coincide up to a sign. To see that the two expressions coincide see [Reference Braverman and Kappeler6, p. 238].
Remark 4.2.1.
is called the
![]() $rho$
invariant
$rho$
invariant
![]() $\rho _{\chi }$
of the operator
$\rho _{\chi }$
of the operator
![]() $B_{\chi }^{\operatorname {\mathrm {even}}}$
.
$B_{\chi }^{\operatorname {\mathrm {even}}}$
.
5 Alternative definition of the refined analytic torsion
In [Reference Braverman and Kappeler6, Section 11], an alternative definition of the refined analytic torsion is given, which involves the Hirzebruch L-polynomial and the signature theorem by Atiyah, Patodi and Singer. We recall this definition here.
Let N be a smooth, oriented, compact, even-dimensional manifold such that
![]() $\partial {N}=X$
. Recall that the signature
$\partial {N}=X$
. Recall that the signature
![]() $\operatorname {\mathrm {sign}}(N)$
is an integer defined in pure cohomological terms (see [Reference Atiyah, Patodi and Singer1, p. 65] and [Reference Atiyah, Patodi and Singer2, p. 407]), as the signature of the Hermitian form, induced by the cup product, in the middle (
$\operatorname {\mathrm {sign}}(N)$
is an integer defined in pure cohomological terms (see [Reference Atiyah, Patodi and Singer1, p. 65] and [Reference Atiyah, Patodi and Singer2, p. 407]), as the signature of the Hermitian form, induced by the cup product, in the middle (
![]() $\dim N/2$
)-cohomology, and it is metric independent. We denote by
$\dim N/2$
)-cohomology, and it is metric independent. We denote by
![]() $L(p)$
the Hirzebruch L-polynomial in the Prontrjagin forms of a Riemannian metric of a manifold ([Reference Lawson and Michelsohn25, p. 228, 232]). The signature theorem ([Reference Atiyah, Patodi and Singer1, Theorem 4.14], [Reference Atiyah, Patodi and Singer2, Theorem 2.2]) states
$L(p)$
the Hirzebruch L-polynomial in the Prontrjagin forms of a Riemannian metric of a manifold ([Reference Lawson and Michelsohn25, p. 228, 232]). The signature theorem ([Reference Atiyah, Patodi and Singer1, Theorem 4.14], [Reference Atiyah, Patodi and Singer2, Theorem 2.2]) states
where
![]() $L_{N}(p):=L(p)$
denotes the Hirzebruch L-polynomial in the Prontrjagin forms of a Riemannian metric on N which is a product near X. By the metric independence of
$L_{N}(p):=L(p)$
denotes the Hirzebruch L-polynomial in the Prontrjagin forms of a Riemannian metric on N which is a product near X. By the metric independence of
![]() $\operatorname {\mathrm {sign}} (N)$
, Equation (5.1) and Proposition 9.5 in [Reference Braverman and Kappeler6], we have that modulo
$\operatorname {\mathrm {sign}} (N)$
, Equation (5.1) and Proposition 9.5 in [Reference Braverman and Kappeler6], we have that modulo
![]() $\mathbb {Z}$
,
$\mathbb {Z}$
,
is independent of the Riemannian metric on X.
In general, there might be no smooth, oriented manifold N such that
![]() $\partial N=X$
. However, since
$\partial N=X$
. However, since
![]() $\dim X$
is odd, there exists an oriented manifold N, whose oriented boundary is the disjoint union of two copies of X, with the same orientation ([Reference Wall50], [44, Th. IV.6.5]). Then, as discussed above, modulo
$\dim X$
is odd, there exists an oriented manifold N, whose oriented boundary is the disjoint union of two copies of X, with the same orientation ([Reference Wall50], [44, Th. IV.6.5]). Then, as discussed above, modulo
![]() $\mathbb {Z}$
,
$\mathbb {Z}$
,
is independent of the Riemannian metric on X.
We assume that the flat connection
![]() $\nabla $
on E belongs to an open neighbourhood, in
$\nabla $
on E belongs to an open neighbourhood, in
![]() $C^{0}$
-topology, of the set of acyclic Hermitian connections (see Subsection 3.2).
$C^{0}$
-topology, of the set of acyclic Hermitian connections (see Subsection 3.2).
Definition 5.1. Let
![]() $\theta \in (-\pi , 0)$
be the Agmon angle of
$\theta \in (-\pi , 0)$
be the Agmon angle of
![]() $B^{\operatorname {\mathrm {even}}}$
. Choose a smooth, compact, oriented manifold N, whose oriented boundary is diffeomorphic to two disjoint copies of M. The refined analytic torsion
$B^{\operatorname {\mathrm {even}}}$
. Choose a smooth, compact, oriented manifold N, whose oriented boundary is diffeomorphic to two disjoint copies of M. The refined analytic torsion
![]() $T'(\nabla )$
is defined by
$T'(\nabla )$
is defined by
where where
![]() $L_{N}(p):=L(p)$
denotes the Hirzebruch L-polynomial in the Prontrjagin forms of a Riemannian metric on N which is a product near
$L_{N}(p):=L(p)$
denotes the Hirzebruch L-polynomial in the Prontrjagin forms of a Riemannian metric on N which is a product near
![]() $\partial N$
.
$\partial N$
.
By the discussion above and the same arguments as in the proof of [Reference Braverman and Kappeler6, Theorem 9.3],
![]() $T'(\nabla )$
is independent the Agmon angle
$T'(\nabla )$
is independent the Agmon angle
![]() $\theta $
and of the Riemannian metric on X. However,
$\theta $
and of the Riemannian metric on X. However,
![]() $T'(\nabla )$
does depend on the choice of N. Since for different choices of N,
$T'(\nabla )$
does depend on the choice of N. Since for different choices of N,
![]() $\int _{N}L(p)$
differs by an integer,
$\int _{N}L(p)$
differs by an integer,
![]() $T'(\nabla )$
is independent of the choice of N up to a multiplication by
$T'(\nabla )$
is independent of the choice of N up to a multiplication by
![]() $i^{k\operatorname {\mathrm {rank}} (E)}$
,
$i^{k\operatorname {\mathrm {rank}} (E)}$
,
![]() $k\in \mathbb {Z}$
. Hence, if
$k\in \mathbb {Z}$
. Hence, if
![]() $\operatorname {\mathrm {rank}} (E)$
is even,
$\operatorname {\mathrm {rank}} (E)$
is even,
![]() $T'(\nabla )$
is well defined up to a sign, and if
$T'(\nabla )$
is well defined up to a sign, and if
![]() $\operatorname {\mathrm {rank}}(E)$
is divisible by
$\operatorname {\mathrm {rank}}(E)$
is divisible by
![]() $4$
, it is a well-defined complex number. In addition, by Equation (5.2) and [Reference Braverman and Kappeler6, Theorem 7.2], we have
$4$
, it is a well-defined complex number. In addition, by Equation (5.2) and [Reference Braverman and Kappeler6, Theorem 7.2], we have
where
![]() $\xi $
is as in Equation (4.2).
$\xi $
is as in Equation (4.2).
6 Cappell–Miller complex torsion
In [Reference Cappell and Miller8], Cappell and Miller introduced the Cappell–Miller torsion
![]() $\tau $
, an invariant, which is an element of
$\tau $
, an invariant, which is an element of
![]() $\det (H^{*}(X,E))\otimes \det (H^{*}(X,E))$
. To define this invariant, they used the flat Laplacian on vector bundle-valued differential forms. This operator is non-self-adjoint and in terms of the chirality operator in the previous sections is the square
$\det (H^{*}(X,E))\otimes \det (H^{*}(X,E))$
. To define this invariant, they used the flat Laplacian on vector bundle-valued differential forms. This operator is non-self-adjoint and in terms of the chirality operator in the previous sections is the square
![]() $B^{2}$
of the odd signature operator B. Hence, roughly speaking, Braverman and Kappeler used the odd signature operator to define the refined analytic torsion and Cappell and Miller its square. By [Reference Braverman and Kappeler5, eq. (5.1)], for a finite-dimensional complex
$B^{2}$
of the odd signature operator B. Hence, roughly speaking, Braverman and Kappeler used the odd signature operator to define the refined analytic torsion and Cappell and Miller its square. By [Reference Braverman and Kappeler5, eq. (5.1)], for a finite-dimensional complex
![]() $(C^{*},\partial )$
,
$(C^{*},\partial )$
,
where
![]() $\rho _{\Gamma }\in \det (H^{*}(\partial ))$
is as in Definition 11.1.1 (Appendix). If the complex
$\rho _{\Gamma }\in \det (H^{*}(\partial ))$
is as in Definition 11.1.1 (Appendix). If the complex
![]() $(C^{*},\partial )$
is acyclic then
$(C^{*},\partial )$
is acyclic then
![]() $\tau _{\Gamma }$
is a complex number and by [Reference Braverman and Kappeler5, eq. (5.3)],
$\tau _{\Gamma }$
is a complex number and by [Reference Braverman and Kappeler5, eq. (5.3)],
 $$ \begin{align} \tau_{\Gamma}:=\prod_{k=0}^{d} \det(B^{2}|_{C^{k}})^{k(-1)^{k+1}}. \end{align} $$
$$ \begin{align} \tau_{\Gamma}:=\prod_{k=0}^{d} \det(B^{2}|_{C^{k}})^{k(-1)^{k+1}}. \end{align} $$
Remark 6.1. As explained in [Reference Braverman and Kappeler5, Remark 5.2], the element
![]() $\tau $
in [Reference Cappell and Miller8] is constructed slightly different. In particular, by the construction of the element
$\tau $
in [Reference Cappell and Miller8] is constructed slightly different. In particular, by the construction of the element
![]() $\rho _{\Gamma }$
and the construction in [Reference Cappell and Miller8, Section 6], the two elements coincide up to a sign. One can see that the signs agree by Equation (6.1) and Equation (6.18) in [Reference Cappell and Miller8].
$\rho _{\Gamma }$
and the construction in [Reference Cappell and Miller8, Section 6], the two elements coincide up to a sign. One can see that the signs agree by Equation (6.1) and Equation (6.18) in [Reference Cappell and Miller8].
In the manifold setting, we consider the Cappell–Miller torsion
![]() $\tau _{\Gamma _{[0,\lambda ]}}\in \det (H^{*}_{[0,\lambda ]}(X,E))\otimes \det (H^{*}_{[0,\lambda ]}(X,E)) $
of the finite-dimensional complex
$\tau _{\Gamma _{[0,\lambda ]}}\in \det (H^{*}_{[0,\lambda ]}(X,E))\otimes \det (H^{*}_{[0,\lambda ]}(X,E)) $
of the finite-dimensional complex
![]() $\Lambda ^{k}_{[0,\lambda ]}(X,E)$
(see Appendix, Subsection 11.2).
$\Lambda ^{k}_{[0,\lambda ]}(X,E)$
(see Appendix, Subsection 11.2).
Definition 6.2. Let
![]() $\theta \in (0,2\pi )$
be an Agmon angle for the operator
$\theta \in (0,2\pi )$
be an Agmon angle for the operator
![]() $B^{2}_{(\lambda ,\infty )}$
. Then, the Cappell–Miller torsion
$B^{2}_{(\lambda ,\infty )}$
. Then, the Cappell–Miller torsion
![]() $\tau _{\nabla }$
is defined by
$\tau _{\nabla }$
is defined by
 $$ \begin{align*} \tau_{\nabla}:= \tau_{\Gamma_{[0,\lambda]}}\prod_{k=0}^{d}{\det}_{\theta}(B^{2}|_{\Lambda^{k}_{(\lambda,\infty)}(X,E)})^{k(-1)^{k+1}}\in \det(H^{*}(X,E))\otimes\det(H^{*}(X,E)). \end{align*} $$
$$ \begin{align*} \tau_{\nabla}:= \tau_{\Gamma_{[0,\lambda]}}\prod_{k=0}^{d}{\det}_{\theta}(B^{2}|_{\Lambda^{k}_{(\lambda,\infty)}(X,E)})^{k(-1)^{k+1}}\in \det(H^{*}(X,E))\otimes\det(H^{*}(X,E)). \end{align*} $$
By [Reference Cappell and Miller8, Theorem 8.3], the Cappell–Miller torsion
![]() $\tau _{\nabla }$
is independent of the choice of
$\tau _{\nabla }$
is independent of the choice of
![]() $\lambda>0$
and the choice of the Riemannian metric on X. Moreover, since the principal symbol of
$\lambda>0$
and the choice of the Riemannian metric on X. Moreover, since the principal symbol of
![]() $B^{2}$
is self-adjoint, by [Reference Braverman and Kappeler6, Section 3.10], the regularized determinant
$B^{2}$
is self-adjoint, by [Reference Braverman and Kappeler6, Section 3.10], the regularized determinant
![]() ${\det }_{\theta }(B^{2}|_{\Lambda ^{k}_{(\lambda ,\infty )}(X,E)})$
is independent of the choice of the Agmon angle
${\det }_{\theta }(B^{2}|_{\Lambda ^{k}_{(\lambda ,\infty )}(X,E)})$
is independent of the choice of the Agmon angle
![]() $\theta $
.
$\theta $
.
Remark 6.3. In the presence of the chirality operator
![]() $\Gamma $
, the dual differential
$\Gamma $
, the dual differential
![]() $\partial ^{*, \sharp }$
, introduced in [Reference Cappell and Miller8] is given by
$\partial ^{*, \sharp }$
, introduced in [Reference Cappell and Miller8] is given by
![]() $\partial ^{*, \sharp }=\Gamma \partial \Gamma $
. Then,
$\partial ^{*, \sharp }=\Gamma \partial \Gamma $
. Then,
![]() $(\partial ^{*, \sharp })^{2}=0$
and one obtains a complex
$(\partial ^{*, \sharp })^{2}=0$
and one obtains a complex
![]() $(\Lambda ^{*}(X,E),\partial ^{*, \sharp })$
of degree
$(\Lambda ^{*}(X,E),\partial ^{*, \sharp })$
of degree
![]() $-1$
. In addition, the flat Laplacian
$-1$
. In addition, the flat Laplacian
![]() $\Delta ^{\sharp }$
acting on
$\Delta ^{\sharp }$
acting on
![]() $\Lambda ^{*}(X,E)$
is given by
$\Lambda ^{*}(X,E)$
is given by
This operator is the same as the square
![]() $B^{2}$
of the odd signature operator, introduced in Section 3. Then, the Cappell–Miller torsion
$B^{2}$
of the odd signature operator, introduced in Section 3. Then, the Cappell–Miller torsion
![]() $\tau $
is defined in terms of the bicomplex
$\tau $
is defined in terms of the bicomplex
![]() $(\Lambda ^{*}(X,E),\partial , \partial ^{*, \sharp })$
. In particular, it is given as a combination of the
$(\Lambda ^{*}(X,E),\partial , \partial ^{*, \sharp })$
. In particular, it is given as a combination of the
![]() $\mathbf {torsion}(\Lambda ^{k}_{[0,\lambda ]}(X,E),\partial ,\partial ^{*, \sharp })\in \det (H^{*}(X,E))\otimes \det (H^{*}(X,E))$
and the square of the
$\mathbf {torsion}(\Lambda ^{k}_{[0,\lambda ]}(X,E),\partial ,\partial ^{*, \sharp })\in \det (H^{*}(X,E))\otimes \det (H^{*}(X,E))$
and the square of the
![]() $\mathbf {Ray-Singer}$
term, which corresponds to the terms
$\mathbf {Ray-Singer}$
term, which corresponds to the terms
![]() $\tau _{\Gamma _{[0,\lambda ]}}$
and
$\tau _{\Gamma _{[0,\lambda ]}}$
and
![]() $\prod _{k=0}^{d} {\det }{\theta }(B^{2}|_{\Lambda ^{k}_{(\lambda ,\infty )}(X,E)})^{k(-1)^{k+1}}$
, respectively, in Definition 9.2.
$\prod _{k=0}^{d} {\det }{\theta }(B^{2}|_{\Lambda ^{k}_{(\lambda ,\infty )}(X,E)})^{k(-1)^{k+1}}$
, respectively, in Definition 9.2.
We turn now to the case, where the flat connection
![]() $\nabla $
on the flat vector bundle belongs to the neighbourhood of the set of all acyclic Hermitian connections. Let
$\nabla $
on the flat vector bundle belongs to the neighbourhood of the set of all acyclic Hermitian connections. Let
![]() $\chi \in V$
, where V is as in Subsection 6.3. Then,
$\chi \in V$
, where V is as in Subsection 6.3. Then,
![]() $B_{\chi }$
is bijective, the cohomologies
$B_{\chi }$
is bijective, the cohomologies
![]() $H^{*}(X,E_{\chi })$
vanish and the element
$H^{*}(X,E_{\chi })$
vanish and the element
![]() $\tau _{\Gamma _{[0,\lambda ]}}$
is equal to
$\tau _{\Gamma _{[0,\lambda ]}}$
is equal to
![]() $1$
. For
$1$
. For
![]() $\chi \in V$
, we define the Cappell–Miller torsion
$\chi \in V$
, we define the Cappell–Miller torsion
![]() $\tau _{\chi }:=\tau (\nabla _{\chi })$
by
$\tau _{\chi }:=\tau (\nabla _{\chi })$
by
 $$ \begin{align} \tau_{\chi}:=\prod_{k=0}^{d} \det(B_{\chi,k}^{2})^{k(-1)^{k+1}}, \end{align} $$
$$ \begin{align} \tau_{\chi}:=\prod_{k=0}^{d} \det(B_{\chi,k}^{2})^{k(-1)^{k+1}}, \end{align} $$
where
![]() $B_{\chi ,k}^{2}$
denotes the operator
$B_{\chi ,k}^{2}$
denotes the operator
![]() $B_{\chi }^{2}$
acting on
$B_{\chi }^{2}$
acting on
![]() $\Lambda ^{k}(X,E)$
. In this case,
$\Lambda ^{k}(X,E)$
. In this case,
![]() $\tau _{\chi }$
is a complex number.
$\tau _{\chi }$
is a complex number.
Proposition 6.4. Let
![]() $\chi \in V$
. Then, the Cappell–Miller torsion
$\chi \in V$
. Then, the Cappell–Miller torsion
![]() $\tau _{\chi }$
and the refined analytic torsion
$\tau _{\chi }$
and the refined analytic torsion
![]() $T_{\chi }$
are related by
$T_{\chi }$
are related by
7 Twisted Selberg and Ruelle zeta functions
In this paper, we are dealing with odd-dimensional, compact, hyperbolic manifolds, obtained as follows. Let
![]() $d=2n+1$
,
$d=2n+1$
,
![]() $n\in \mathbb {N}_{>0}$
. We consider the universal coverings
$n\in \mathbb {N}_{>0}$
. We consider the universal coverings
![]() $G=\operatorname {\mathrm {Spin}}(d,1)$
of
$G=\operatorname {\mathrm {Spin}}(d,1)$
of
![]() $\mathrm {SO}^0(d,1)$
and
$\mathrm {SO}^0(d,1)$
and
![]() $K=\operatorname {\mathrm {Spin}}(d)$
of
$K=\operatorname {\mathrm {Spin}}(d)$
of
![]() $\mathrm {SO}(d)$
, respectively. We set
$\mathrm {SO}(d)$
, respectively. We set
![]() $\widetilde {X}:=G/K$
. Let
$\widetilde {X}:=G/K$
. Let
![]() $\mathfrak {g},\mathfrak {k}$
be the Lie algebras of G and K, respectively. Let
$\mathfrak {g},\mathfrak {k}$
be the Lie algebras of G and K, respectively. Let
![]() $\Theta $
be the Cartan involution of G and
$\Theta $
be the Cartan involution of G and
![]() $\theta $
the differential of
$\theta $
the differential of
![]() $\Theta $
at e, where e is the identity element of G. Let
$\Theta $
at e, where e is the identity element of G. Let
![]() $ \mathfrak {g}=\mathfrak {k}\oplus \mathfrak {p}$
be the Cartan decomposition of
$ \mathfrak {g}=\mathfrak {k}\oplus \mathfrak {p}$
be the Cartan decomposition of
![]() $\mathfrak {g}$
with respect to
$\mathfrak {g}$
with respect to
![]() $\theta $
. There exists a canonical isomorphism
$\theta $
. There exists a canonical isomorphism
![]() $T_{eK}\cong \mathfrak {p}$
. Let
$T_{eK}\cong \mathfrak {p}$
. Let
![]() $B(X,Y)$
be the Killing form on
$B(X,Y)$
be the Killing form on
![]() $\mathfrak {g}\times \mathfrak {g}$
defined by
$\mathfrak {g}\times \mathfrak {g}$
defined by
![]() $ B(X,Y)=\operatorname {\mathrm {Tr}} (\operatorname {\mathrm {ad}}(X)\circ \operatorname {\mathrm {ad}}(Y))$
. It is a symmetric bilinear form. We set
$ B(X,Y)=\operatorname {\mathrm {Tr}} (\operatorname {\mathrm {ad}}(X)\circ \operatorname {\mathrm {ad}}(Y))$
. It is a symmetric bilinear form. We set
The restriction of
![]() $\langle \cdot ,\cdot \rangle $
to
$\langle \cdot ,\cdot \rangle $
to
![]() $\mathfrak {p}$
defines an inner product on
$\mathfrak {p}$
defines an inner product on
![]() $\mathfrak {p}$
and therefore induces a G-invariant Riemannian metric on
$\mathfrak {p}$
and therefore induces a G-invariant Riemannian metric on
![]() $\widetilde {X}$
, which has constant curvature
$\widetilde {X}$
, which has constant curvature
![]() $-1$
. Then,
$-1$
. Then,
![]() $\widetilde {X}$
equipped with this metric is isometric to
$\widetilde {X}$
equipped with this metric is isometric to
![]() ${\mathbb {H}}^{d}$
. Let
${\mathbb {H}}^{d}$
. Let
![]() $\Gamma _{1}$
be a torsion-free, cocompact, discrete subgroup of
$\Gamma _{1}$
be a torsion-free, cocompact, discrete subgroup of
![]() $\mathrm {SO}^0(d,1)$
. We assume that
$\mathrm {SO}^0(d,1)$
. We assume that
![]() $\Gamma _{1}$
can be lifted to a subgroup
$\Gamma _{1}$
can be lifted to a subgroup
![]() $\Gamma $
of G. Then,
$\Gamma $
of G. Then,
![]() $X:=\Gamma \backslash \widetilde {X}$
is a compact, hyperbolic manifold of odd dimension d.
$X:=\Gamma \backslash \widetilde {X}$
is a compact, hyperbolic manifold of odd dimension d.
7.1 Representation theory of Lie groups
Let
be the standard Iwasawa decomposition of G, and let M be the centralizer of A in K. Then,
![]() $M=\operatorname {\mathrm {Spin}}(d-1)$
. Let
$M=\operatorname {\mathrm {Spin}}(d-1)$
. Let
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {m}$
be the Lie algebras of A and M, respectively. Let
$\mathfrak {m}$
be the Lie algebras of A and M, respectively. Let
![]() $\mathfrak {b}$
be a Cartan subalgebra of
$\mathfrak {b}$
be a Cartan subalgebra of
![]() $\mathfrak {m}$
. Let
$\mathfrak {m}$
. Let
![]() $\mathfrak {h}$
be a Cartan subalgebra of
$\mathfrak {h}$
be a Cartan subalgebra of
![]() $\mathfrak {g}$
. We consider the complexifications
$\mathfrak {g}$
. We consider the complexifications
![]() $\mathfrak {g}_{\mathbb {C}}:=\mathfrak {g}\oplus i\mathfrak {g}$
,
$\mathfrak {g}_{\mathbb {C}}:=\mathfrak {g}\oplus i\mathfrak {g}$
,
![]() $\mathfrak {h}_{\mathbb {C}}:=\mathfrak {h}\oplus i\mathfrak {h}$
and
$\mathfrak {h}_{\mathbb {C}}:=\mathfrak {h}\oplus i\mathfrak {h}$
and
![]() $\mathfrak {m}_{\mathbb {C}}:=\mathfrak {m}\oplus i\mathfrak {m}$
.
$\mathfrak {m}_{\mathbb {C}}:=\mathfrak {m}\oplus i\mathfrak {m}$
.
Let
![]() $\Delta ^{+}(\mathfrak {g},\mathfrak {a})$
be the set of positive roots of
$\Delta ^{+}(\mathfrak {g},\mathfrak {a})$
be the set of positive roots of
![]() $(\mathfrak {g},\mathfrak {a})$
and
$(\mathfrak {g},\mathfrak {a})$
and
![]() $\mathfrak {g}_{\alpha }$
the corresponding root spaces. In the present case,
$\mathfrak {g}_{\alpha }$
the corresponding root spaces. In the present case,
![]() $\Delta ^{+}(\mathfrak {g},\mathfrak {a})$
consists of a single root
$\Delta ^{+}(\mathfrak {g},\mathfrak {a})$
consists of a single root
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $M'=\operatorname {\mathrm {Norm}}_{K}(A)$
be the normalizer of A in K. Let
$M'=\operatorname {\mathrm {Norm}}_{K}(A)$
be the normalizer of A in K. Let
![]() $H\in \mathfrak {a}$
such that
$H\in \mathfrak {a}$
such that
![]() $\alpha (H)=1$
. With respect to the inner product, induced by (2.1) on
$\alpha (H)=1$
. With respect to the inner product, induced by (2.1) on
![]() $\mathfrak {a}$
, H has norm 1. We define
$\mathfrak {a}$
, H has norm 1. We define
 $$ \begin{align} \rho_{\mathfrak{m}}:=\frac{1}{2}\sum_{\alpha\in \Delta^+(\mathfrak{m}_{\mathbb{C}},\mathfrak{b})}\alpha. \end{align} $$
$$ \begin{align} \rho_{\mathfrak{m}}:=\frac{1}{2}\sum_{\alpha\in \Delta^+(\mathfrak{m}_{\mathbb{C}},\mathfrak{b})}\alpha. \end{align} $$
The inclusion
![]() $i\colon M\hookrightarrow K$
induces the restriction map
$i\colon M\hookrightarrow K$
induces the restriction map
![]() $i^{*}\colon R(K)\rightarrow R(M)$
, where
$i^{*}\colon R(K)\rightarrow R(M)$
, where
![]() $R(K),R(M)$
are the representation rings over
$R(K),R(M)$
are the representation rings over
![]() $\mathbb {Z}$
of K and M, respectively. Let
$\mathbb {Z}$
of K and M, respectively. Let
![]() $\widehat {K},\widehat {M}$
be the sets of equivalent classes of irreducible unitary representations of K and M, respectively. For the highest weight
$\widehat {K},\widehat {M}$
be the sets of equivalent classes of irreducible unitary representations of K and M, respectively. For the highest weight
![]() $\nu _{\tau }$
of
$\nu _{\tau }$
of
![]() $\tau \in \widehat {K}$
, we have
$\tau \in \widehat {K}$
, we have
![]() $\nu _{\tau }=(\nu _{1},\ldots ,\nu _{n})$
, where
$\nu _{\tau }=(\nu _{1},\ldots ,\nu _{n})$
, where
![]() $\nu _{1}\geq \ldots \geq \nu _{n}$
and
$\nu _{1}\geq \ldots \geq \nu _{n}$
and
![]() $\nu _{i},i=1,\ldots ,n$
are all half integers (i.e.,
$\nu _{i},i=1,\ldots ,n$
are all half integers (i.e.,
![]() $\nu _{i}=q_{i}+\frac {1}{2}$
,
$\nu _{i}=q_{i}+\frac {1}{2}$
,
![]() $q_{i}\in \mathbb {Z}$
). For the highest weight
$q_{i}\in \mathbb {Z}$
). For the highest weight
![]() $\nu _{\sigma }$
of
$\nu _{\sigma }$
of
![]() $\sigma \in \widehat {M}$
, we have
$\sigma \in \widehat {M}$
, we have
where
![]() $\nu _{1}\geq \ldots \geq \nu _{n-1}\geq \lvert \nu _{n}\rvert $
and
$\nu _{1}\geq \ldots \geq \nu _{n-1}\geq \lvert \nu _{n}\rvert $
and
![]() $\nu _{i},i=1,\ldots ,n$
are all half integers ([Reference Bunke and Olbrich7, p. 20]). We denote by
$\nu _{i},i=1,\ldots ,n$
are all half integers ([Reference Bunke and Olbrich7, p. 20]). We denote by
![]() $(s,S)$
be the spin representation of K and by
$(s,S)$
be the spin representation of K and by
![]() $(s^{+},S^{+})$
,
$(s^{+},S^{+})$
,
![]() $(s^{-},S^{-})$
the half spin representations of M ([Reference Friedrich20, p. 22]).
$(s^{-},S^{-})$
the half spin representations of M ([Reference Friedrich20, p. 22]).
7.2 The Casimir element
Let
![]() $Z_{i}$
be a basis of
$Z_{i}$
be a basis of
![]() $\mathfrak {g}$
, and let
$\mathfrak {g}$
, and let
![]() $Z^{j}$
be the basis of
$Z^{j}$
be the basis of
![]() $\mathfrak {g}$
, which is determined by
$\mathfrak {g}$
, which is determined by
![]() $\langle Z_{i}, Z^{j} \rangle =\delta _{ij}$
, where
$\langle Z_{i}, Z^{j} \rangle =\delta _{ij}$
, where
![]() $\langle \cdot , \cdot \rangle $
is as in Equation (7.1). Let
$\langle \cdot , \cdot \rangle $
is as in Equation (7.1). Let
![]() $\mathcal {U}(\mathfrak {g}_{\mathbb {C}})$
be the universal enveloping algebra of
$\mathcal {U}(\mathfrak {g}_{\mathbb {C}})$
be the universal enveloping algebra of
![]() $\mathfrak {g}_{\mathbb {C}}$
, and let
$\mathfrak {g}_{\mathbb {C}}$
, and let
![]() $Z(\mathfrak {g}_{\mathbb {C}})$
be its center. Then,
$Z(\mathfrak {g}_{\mathbb {C}})$
be its center. Then,
![]() $\Omega \in Z(\mathfrak {g}_{\mathbb {C}})$
is given by
$\Omega \in Z(\mathfrak {g}_{\mathbb {C}})$
is given by
By Kuga’s Lemma ([Reference Matsushima and Murakami28, (6.9)]), the Hodge Laplacian, acting on the space
![]() $\Lambda ^{*}(G/K)$
of differential forms on
$\Lambda ^{*}(G/K)$
of differential forms on
![]() $G/K$
, coincides with
$G/K$
, coincides with
![]() $-R(\Omega )$
, where
$-R(\Omega )$
, where
![]() $R(\Omega )$
is the Casimir operator on
$R(\Omega )$
is the Casimir operator on
![]() $\Lambda ^{*}(G/K)$
, induced by
$\Lambda ^{*}(G/K)$
, induced by
![]() $\Omega $
.
$\Omega $
.
7.3 Definition of the twisted dynamical zeta functions
We consider the twisted Ruelle and Selberg zeta functions associated with the geodesic flow on the sphere vector bundle
![]() $S(X)$
of
$S(X)$
of
![]() $X=\Gamma \backslash G/ K$
. Since K acts transitively on the unit vectors in
$X=\Gamma \backslash G/ K$
. Since K acts transitively on the unit vectors in
![]() $\mathfrak {p}$
,
$\mathfrak {p}$
,
![]() $S(\widetilde {X})$
can be represented by the homogeneous space
$S(\widetilde {X})$
can be represented by the homogeneous space
![]() $G/M$
. Therefore
$G/M$
. Therefore
![]() $S(X)=\Gamma \backslash G/M$
.
$S(X)=\Gamma \backslash G/M$
.
We recall the Cartan decomposition
![]() $G=KA^{+}K$
of G, where
$G=KA^{+}K$
of G, where
![]() $A^{+}$
is as in Equation (7.2). Then, every element
$A^{+}$
is as in Equation (7.2). Then, every element
![]() $g\in G$
can be written as
$g\in G$
can be written as
![]() $g=ha_{+}k$
, where
$g=ha_{+}k$
, where
![]() $h,k\in K$
and
$h,k\in K$
and
![]() $a_{+}=\exp (tH)$
, for some
$a_{+}=\exp (tH)$
, for some
![]() $t\in \mathbb {R}^{+}$
. The positive real number t equals
$t\in \mathbb {R}^{+}$
. The positive real number t equals
![]() $d(eK,gK)$
, where
$d(eK,gK)$
, where
![]() $d(\cdot ,\cdot )$
denotes the geodesic distance on
$d(\cdot ,\cdot )$
denotes the geodesic distance on
![]() $\widetilde {X}$
. It is a well-known fact that there is a one-to-one correspondence between the closed geodesics on a manifold X with negative sectional curvature and the nontrivial conjugacy classes of the fundamental group
$\widetilde {X}$
. It is a well-known fact that there is a one-to-one correspondence between the closed geodesics on a manifold X with negative sectional curvature and the nontrivial conjugacy classes of the fundamental group
![]() $\pi _{1}(X)$
of X ([Reference Gromoll, Klingenberg and Meyer22]).
$\pi _{1}(X)$
of X ([Reference Gromoll, Klingenberg and Meyer22]).
The hyperbolic elements of
![]() $\Gamma $
can be realized as the semisimple elements of this group, that is, the diagonalizable elements of
$\Gamma $
can be realized as the semisimple elements of this group, that is, the diagonalizable elements of
![]() $\Gamma $
. Since
$\Gamma $
. Since
![]() $\Gamma $
is a cocompact subgroup of G, every element
$\Gamma $
is a cocompact subgroup of G, every element
![]() $\gamma \in \Gamma -\{e\}$
hyperbolic. We denote by
$\gamma \in \Gamma -\{e\}$
hyperbolic. We denote by
![]() $c_{\gamma }$
the closed geodesic on X, associated with the hyperbolic conjugacy class
$c_{\gamma }$
the closed geodesic on X, associated with the hyperbolic conjugacy class
![]() $[\gamma ]$
. We denote by
$[\gamma ]$
. We denote by
![]() $l(\gamma )$
the length of
$l(\gamma )$
the length of
![]() $c_{\gamma }$
. Since
$c_{\gamma }$
. Since
![]() $\Gamma $
is torsion-free,
$\Gamma $
is torsion-free,
![]() $l(\gamma )$
is always positive and therefore we can obtain an infimum for the length spectrum
$l(\gamma )$
is always positive and therefore we can obtain an infimum for the length spectrum
![]() $\operatorname {\mathrm {spec}}(\Gamma ):=\{l(\gamma )\colon \gamma \in \Gamma \}$
. An element
$\operatorname {\mathrm {spec}}(\Gamma ):=\{l(\gamma )\colon \gamma \in \Gamma \}$
. An element
![]() $\gamma \in \Gamma $
is called primitive if there exists no
$\gamma \in \Gamma $
is called primitive if there exists no
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n>1$
and
$n>1$
and
![]() $\gamma _{0}\in \Gamma $
such that
$\gamma _{0}\in \Gamma $
such that
![]() $\gamma =\gamma _{0}^{n}$
. A primitive element
$\gamma =\gamma _{0}^{n}$
. A primitive element
![]() $\gamma _{0}\in \Gamma $
corresponds to a geodesic on X. The prime geodesics correspond to the periodic orbits of minimal length. Hence, if a hyperbolic element
$\gamma _{0}\in \Gamma $
corresponds to a geodesic on X. The prime geodesics correspond to the periodic orbits of minimal length. Hence, if a hyperbolic element
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma $
is generated by a primitive element
$\Gamma $
is generated by a primitive element
![]() $\gamma _{0}$
, then there exists a
$\gamma _{0}$
, then there exists a
![]() $n_{\Gamma }(\gamma )\in \mathbb {N}$
such that
$n_{\Gamma }(\gamma )\in \mathbb {N}$
such that
![]() $\gamma =\gamma _{0}^{n_{\Gamma }(\gamma )}$
and the corresponding closed geodesic is of length
$\gamma =\gamma _{0}^{n_{\Gamma }(\gamma )}$
and the corresponding closed geodesic is of length
![]() $l(\gamma )=n_{\Gamma }(\gamma )l(\gamma _{0})$
.
$l(\gamma )=n_{\Gamma }(\gamma )l(\gamma _{0})$
.
We lift now the closed geodesic
![]() $c_{\gamma }$
to the universal covering
$c_{\gamma }$
to the universal covering
![]() $\widetilde {X}$
. For
$\widetilde {X}$
. For
![]() $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
![]() $l(\gamma ):=\inf \{d(x,\gamma x)\colon x\in \widetilde {X}\}$
, or
$l(\gamma ):=\inf \{d(x,\gamma x)\colon x\in \widetilde {X}\}$
, or
![]() $l(\gamma )=\inf \{d(eK,g^{-1}\gamma gK)\colon g\in G\}$
. Hence, we see that the length of the closed geodesic
$l(\gamma )=\inf \{d(eK,g^{-1}\gamma gK)\colon g\in G\}$
. Hence, we see that the length of the closed geodesic
![]() $l(\gamma )$
depends only on
$l(\gamma )$
depends only on
![]() $\gamma \in \Gamma $
. Let
$\gamma \in \Gamma $
. Let
![]() $\gamma \in \Gamma $
, with
$\gamma \in \Gamma $
, with
![]() $ \gamma \neq e$
. Then, by [Reference Wallach51, Lemma 6.5] there exist a
$ \gamma \neq e$
. Then, by [Reference Wallach51, Lemma 6.5] there exist a
![]() $g\in G$
, a
$g\in G$
, a
![]() $m_{\gamma } \in M$
, and an
$m_{\gamma } \in M$
, and an
![]() $a_{\gamma } \in A^{+}$
such that
$a_{\gamma } \in A^{+}$
such that
![]() $ g^{-1}\gamma g=m_{\gamma }a_{\gamma }$
. The element
$ g^{-1}\gamma g=m_{\gamma }a_{\gamma }$
. The element
![]() $m_{\gamma }$
is determined up to conjugacy in M, and the element
$m_{\gamma }$
is determined up to conjugacy in M, and the element
![]() $a_{\gamma }$
depends only on
$a_{\gamma }$
depends only on
![]() $\gamma $
. As in [Reference Bunke and Olbrich7, Section 3.1], we consider the geodesic flow
$\gamma $
. As in [Reference Bunke and Olbrich7, Section 3.1], we consider the geodesic flow
![]() $\phi $
on
$\phi $
on
![]() $S(X)$
, given by the map
$S(X)$
, given by the map
![]() $ \phi \colon \mathbb {R}\times S(X)\ni (t,\Gamma gM)\rightarrow \Gamma g\exp (-tH) M \in S(X) $
. A closed orbit of
$ \phi \colon \mathbb {R}\times S(X)\ni (t,\Gamma gM)\rightarrow \Gamma g\exp (-tH) M \in S(X) $
. A closed orbit of
![]() $\phi $
is described by the set
$\phi $
is described by the set
![]() $c:=\{\Gamma g\exp (-tH) M\colon t\in \mathbb {R}\}$
, where
$c:=\{\Gamma g\exp (-tH) M\colon t\in \mathbb {R}\}$
, where
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $g^{-1}\gamma g:=m_{\gamma }a_{\gamma }\in MA^{+}$
. The Anosov property of the geodesic flow
$g^{-1}\gamma g:=m_{\gamma }a_{\gamma }\in MA^{+}$
. The Anosov property of the geodesic flow
![]() $\phi $
on
$\phi $
on
![]() $S(X)$
can be expressed by the following
$S(X)$
can be expressed by the following
![]() $d\phi $
-invariant splitting of
$d\phi $
-invariant splitting of
![]() $TS(X)$
$TS(X)$
where
![]() $T^sS(X)$
consists of vectors that shrink exponentially,
$T^sS(X)$
consists of vectors that shrink exponentially,
![]() $T^uS(X)$
consists of vectors that expand exponentially, and
$T^uS(X)$
consists of vectors that expand exponentially, and
![]() $T^{c}S(X)$
is the one-dimensional subspace of vectors tangent to the flow, with respect to the Riemannian metric, as
$T^{c}S(X)$
is the one-dimensional subspace of vectors tangent to the flow, with respect to the Riemannian metric, as
![]() $t\rightarrow \infty $
. The splitting in Equation (7.6) corresponds to the splitting
$t\rightarrow \infty $
. The splitting in Equation (7.6) corresponds to the splitting
where
![]() $\operatorname {\mathrm {Ad}}$
denotes the adjoint action of
$\operatorname {\mathrm {Ad}}$
denotes the adjoint action of
![]() $\operatorname {\mathrm {Ad}}(\exp (-tH))$
on
$\operatorname {\mathrm {Ad}}(\exp (-tH))$
on
![]() $\overline {\mathfrak {n}}, \mathfrak {a},\mathfrak {n}$
, and
$\overline {\mathfrak {n}}, \mathfrak {a},\mathfrak {n}$
, and
![]() $\overline {\mathfrak {n}}=\theta \mathfrak {n}$
is the sum of the negative root spaces of the system
$\overline {\mathfrak {n}}=\theta \mathfrak {n}$
is the sum of the negative root spaces of the system
![]() $(\mathfrak {g},\mathfrak {a})$
.
$(\mathfrak {g},\mathfrak {a})$
.
Definition 7.3.1. Let
![]() $\chi \colon \Gamma \rightarrow \operatorname {\mathrm {GL}}(V_{\chi })$
be a finite-dimensional, complex representation of
$\chi \colon \Gamma \rightarrow \operatorname {\mathrm {GL}}(V_{\chi })$
be a finite-dimensional, complex representation of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\sigma \in \widehat {M}$
. The twisted Selberg zeta function
$\sigma \in \widehat {M}$
. The twisted Selberg zeta function
![]() $Z(s;\sigma ,\chi )$
is defined by the infinite product
$Z(s;\sigma ,\chi )$
is defined by the infinite product
 $$ \begin{align*} Z(s;\sigma,\chi):=\prod_{\substack{[\gamma]\neq{e}\\ [\gamma]\operatorname{\mathrm{prime}}}} \prod_{k=0}^{\infty}\det\big(\operatorname{\mathrm{Id}}-(\chi(\gamma)\otimes\sigma(m_\gamma)\otimes S^k(\operatorname{\mathrm{Ad}}(m_\gamma a_\gamma)|_{\overline{\mathfrak{n}}})) e^{-(s+|\rho|)\lvert l(\gamma)}\big), \end{align*} $$
$$ \begin{align*} Z(s;\sigma,\chi):=\prod_{\substack{[\gamma]\neq{e}\\ [\gamma]\operatorname{\mathrm{prime}}}} \prod_{k=0}^{\infty}\det\big(\operatorname{\mathrm{Id}}-(\chi(\gamma)\otimes\sigma(m_\gamma)\otimes S^k(\operatorname{\mathrm{Ad}}(m_\gamma a_\gamma)|_{\overline{\mathfrak{n}}})) e^{-(s+|\rho|)\lvert l(\gamma)}\big), \end{align*} $$
where
![]() $s\in \mathbb {C}$
,
$s\in \mathbb {C}$
,
![]() $S^k(\operatorname {\mathrm {Ad}}(m_\gamma a_\gamma )_{\overline {\mathfrak {n}}})$
denotes the k-th symmetric power of the adjoint map
$S^k(\operatorname {\mathrm {Ad}}(m_\gamma a_\gamma )_{\overline {\mathfrak {n}}})$
denotes the k-th symmetric power of the adjoint map
![]() $\operatorname {\mathrm {Ad}}(m_\gamma a_\gamma )$
restricted to
$\operatorname {\mathrm {Ad}}(m_\gamma a_\gamma )$
restricted to
![]() $\mathfrak {\overline {n}}$
and
$\mathfrak {\overline {n}}$
and
![]() $\rho $
is as in Equation (7.3).
$\rho $
is as in Equation (7.3).
By [Reference Spilioti48, Proposition 3.4], there exists a positive constant c such that the twisted Selberg zeta function
![]() $Z(s;\sigma ,\chi )$
converges absolutely and uniformly on compact subsets of the half-plane
$Z(s;\sigma ,\chi )$
converges absolutely and uniformly on compact subsets of the half-plane
![]() $\operatorname {\mathrm {Re}}(s)>c$
.
$\operatorname {\mathrm {Re}}(s)>c$
.
Definition 7.3.2. Let
![]() $\chi \colon \Gamma \rightarrow \operatorname {\mathrm {GL}}(V_{\chi })$
be a finite-dimensional, complex representation of
$\chi \colon \Gamma \rightarrow \operatorname {\mathrm {GL}}(V_{\chi })$
be a finite-dimensional, complex representation of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\sigma \in \widehat {M}$
. The twisted Ruelle zeta function
$\sigma \in \widehat {M}$
. The twisted Ruelle zeta function
![]() $ R(s;\sigma ,\chi )$
is defined by the infinite product
$ R(s;\sigma ,\chi )$
is defined by the infinite product
 $$ \begin{align*} R(s;\sigma,\chi):=\prod_{\substack{[\gamma]\neq{e}\\ [\gamma]\operatorname{\mathrm{prime}}}}\det\big(\operatorname{\mathrm{Id}}-(\chi(\gamma)\otimes\sigma(m_{\gamma}))e^{-sl(\gamma)}\big)^{(-1)^{d-1}}, \end{align*} $$
$$ \begin{align*} R(s;\sigma,\chi):=\prod_{\substack{[\gamma]\neq{e}\\ [\gamma]\operatorname{\mathrm{prime}}}}\det\big(\operatorname{\mathrm{Id}}-(\chi(\gamma)\otimes\sigma(m_{\gamma}))e^{-sl(\gamma)}\big)^{(-1)^{d-1}}, \end{align*} $$
where
![]() $s\in \mathbb {C}$
.
$s\in \mathbb {C}$
.
By [Reference Spilioti48, Proposition 3.5], there exists a positive constant r such that the twisted Selberg zeta function
![]() $R(s;\sigma ,\chi )$
converges absolutely and uniformly on compact subsets of the half-plane
$R(s;\sigma ,\chi )$
converges absolutely and uniformly on compact subsets of the half-plane
![]() $\operatorname {\mathrm {Re}}(s)>r$
.
$\operatorname {\mathrm {Re}}(s)>r$
.
The twisted dynamical zeta functions associated with an arbitrary representation of
![]() $\Gamma $
has been studied in [Reference Spilioti48] and [Reference Spilioti49]. Specifically, by [Reference Spilioti48, Theorem 1.1 and Theorem 1.2], the twisted dynamical zeta functions admit a meromorphic continuation to the whole complex plane.
$\Gamma $
has been studied in [Reference Spilioti48] and [Reference Spilioti49]. Specifically, by [Reference Spilioti48, Theorem 1.1 and Theorem 1.2], the twisted dynamical zeta functions admit a meromorphic continuation to the whole complex plane.
8 Harmonic analysis on symmetric spaces
8.1 Twisted Bochner–Laplace operator
In this section, we define the twisted Bochner–Laplace operator as it is introduced in [Reference Müller35, Section 4]. In addition, we describe this operator in the locally symmetric space setting.
Let
![]() $E_{0}\rightarrow X$
be a complex vector bundle with covariant derivative
$E_{0}\rightarrow X$
be a complex vector bundle with covariant derivative
![]() $\nabla $
. We define the second covariant derivative
$\nabla $
. We define the second covariant derivative
![]() $\nabla ^2$
by
$\nabla ^2$
by
where
![]() $V,W\in C^{\infty }(X,TX)$
and
$V,W\in C^{\infty }(X,TX)$
and
![]() $\nabla ^{LC}$
denotes the Levi–Civita connection on
$\nabla ^{LC}$
denotes the Levi–Civita connection on
![]() $TX$
. We define the connection Laplacian
$TX$
. We define the connection Laplacian
![]() $\Delta _{E_{0}}$
to be the negative of the trace of the second covariant derivative, that is,
$\Delta _{E_{0}}$
to be the negative of the trace of the second covariant derivative, that is,
If
![]() $E_{0}$
is equipped with a Hermitian metric compatible with the connection
$E_{0}$
is equipped with a Hermitian metric compatible with the connection
![]() $\nabla $
, then by [Reference Lawson and Michelsohn25, p. 154], the connection Laplacian is equal to the Bochner–Laplace operator, that is,
$\nabla $
, then by [Reference Lawson and Michelsohn25, p. 154], the connection Laplacian is equal to the Bochner–Laplace operator, that is,
In terms of a local orthonormal frame field
![]() $(e_{1},\ldots ,e_{d})$
of
$(e_{1},\ldots ,e_{d})$
of
![]() $T_{x}X$
, for
$T_{x}X$
, for
![]() $x\in X$
, the connection Laplacian is given by
$x\in X$
, the connection Laplacian is given by
 $$ \begin{align*} \Delta_{E_{0}}=-\sum_{j=1}^{d}\nabla^ 2{{}_{e_j,e_j}}. \end{align*} $$
$$ \begin{align*} \Delta_{E_{0}}=-\sum_{j=1}^{d}\nabla^ 2{{}_{e_j,e_j}}. \end{align*} $$
The principal symbol of
![]() $\Delta _{E_{0}}$
equals
$\Delta _{E_{0}}$
equals
where
![]() $x\in X$
and
$x\in X$
and
![]() $\xi \in \operatorname {\mathrm {T}}_{x}^{*}X$
.
$\xi \in \operatorname {\mathrm {T}}_{x}^{*}X$
.
![]() $\Delta _{E_{0}}$
acts in
$\Delta _{E_{0}}$
acts in
![]() $L^{2}(X,E_{0})$
with domain
$L^{2}(X,E_{0})$
with domain
![]() $C^{\infty }(X,E_{0})$
. The operator
$C^{\infty }(X,E_{0})$
. The operator
![]() $\Delta _{E_{0}}\colon C^{\infty }(X,E_{0})\circlearrowright $
is a second order, elliptic, formally self-adjoint differential operator.
$\Delta _{E_{0}}\colon C^{\infty }(X,E_{0})\circlearrowright $
is a second order, elliptic, formally self-adjoint differential operator.
Let
![]() $\chi \colon \Gamma \rightarrow \operatorname {\mathrm {GL}}(V_{\chi })$
be a finite-dimensional, complex representation of
$\chi \colon \Gamma \rightarrow \operatorname {\mathrm {GL}}(V_{\chi })$
be a finite-dimensional, complex representation of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $E_{\chi }\rightarrow X$
be the associated flat vector bundle over X, equipped with a flat connection
$E_{\chi }\rightarrow X$
be the associated flat vector bundle over X, equipped with a flat connection
![]() $\nabla ^{E_{\chi }}$
. We specialize to the twisted case
$\nabla ^{E_{\chi }}$
. We specialize to the twisted case
![]() $E=E_{0}\otimes E_{\chi }$
, where
$E=E_{0}\otimes E_{\chi }$
, where
![]() $E_{0}\rightarrow X$
is a complex vector bundle equipped with a connection
$E_{0}\rightarrow X$
is a complex vector bundle equipped with a connection
![]() $\nabla ^{E_{0}}$
and a metric, which is compatible with this connection. Let
$\nabla ^{E_{0}}$
and a metric, which is compatible with this connection. Let
![]() $\nabla ^{E}=\nabla ^{E_{0}\otimes E_{\chi }}$
be the product connection, defined by
$\nabla ^{E}=\nabla ^{E_{0}\otimes E_{\chi }}$
be the product connection, defined by
We define the operator
![]() $\Delta _{E_{0},\chi }^\sharp $
by
$\Delta _{E_{0},\chi }^\sharp $
by
We choose a Hermitian metric in
![]() $E_{\chi }$
. Then,
$E_{\chi }$
. Then,
![]() $\Delta _{E_{0},\chi }^{\sharp }$
acts on
$\Delta _{E_{0},\chi }^{\sharp }$
acts on
![]() $L^{2}(X,E_{0}\otimes E_{\chi })$
. However, it is not a formally self-adjoint operator in general. We want to describe this operator locally. Following the analysis in [Reference Müller35], we consider an open subset U of X such that
$L^{2}(X,E_{0}\otimes E_{\chi })$
. However, it is not a formally self-adjoint operator in general. We want to describe this operator locally. Following the analysis in [Reference Müller35], we consider an open subset U of X such that
![]() $E_{\chi }\lvert _{U}$
is trivial. Then,
$E_{\chi }\lvert _{U}$
is trivial. Then,
![]() $E_{0}\otimes E_{\chi }\lvert _{U}$
is isomorphic to the direct sum of m-copies of
$E_{0}\otimes E_{\chi }\lvert _{U}$
is isomorphic to the direct sum of m-copies of
![]() $E_{0}\lvert _{U}$
, that is,
$E_{0}\lvert _{U}$
, that is,
where
![]() $m:=\operatorname {\mathrm {rank}}(E_\chi )=\dim V_{\chi }$
. Let
$m:=\operatorname {\mathrm {rank}}(E_\chi )=\dim V_{\chi }$
. Let
![]() $(e_{i}),i=1,\ldots ,m$
be any basis of flat sections of
$(e_{i}),i=1,\ldots ,m$
be any basis of flat sections of
![]() $E_{\chi }\lvert _{U}$
. Then, each
$E_{\chi }\lvert _{U}$
. Then, each
![]() $\phi \in C^{\infty }(U,(E_{0}\otimes E_{\chi })\lvert _{U})$
can be written as
$\phi \in C^{\infty }(U,(E_{0}\otimes E_{\chi })\lvert _{U})$
can be written as
 $$ \begin{align*} \phi=\sum_{i=1}^{m}\phi_{i} \otimes e_{i}, \end{align*} $$
$$ \begin{align*} \phi=\sum_{i=1}^{m}\phi_{i} \otimes e_{i}, \end{align*} $$
where
![]() $\phi _{i}\in C^{\infty }(U, E_{0}\lvert _{U}), i=1,\ldots ,m$
. The product connection is given by
$\phi _{i}\in C^{\infty }(U, E_{0}\lvert _{U}), i=1,\ldots ,m$
. The product connection is given by
 $$ \begin{align*} \nabla_{Y}^{E_{0}\otimes E_{\chi}}\phi=\sum_{i=1}^{m}(\nabla_{Y}^{E_{0}})(\phi_{i})\otimes e_{i}, \end{align*} $$
$$ \begin{align*} \nabla_{Y}^{E_{0}\otimes E_{\chi}}\phi=\sum_{i=1}^{m}(\nabla_{Y}^{E_{0}})(\phi_{i})\otimes e_{i}, \end{align*} $$
where
![]() $Y\in C^{\infty }(X,TX)$
. The local expression above is independent of the choice of the base of flat sections of
$Y\in C^{\infty }(X,TX)$
. The local expression above is independent of the choice of the base of flat sections of
![]() $E_{\chi }\vert _{U}$
since the transition maps comparing flat sections are constant. By Equation (8.1), we obtain the twisted Bochner–Laplace operator acting on
$E_{\chi }\vert _{U}$
since the transition maps comparing flat sections are constant. By Equation (8.1), we obtain the twisted Bochner–Laplace operator acting on
![]() $C^{\infty }(X,E_{0}\otimes E_{\chi })$
given by
$C^{\infty }(X,E_{0}\otimes E_{\chi })$
given by
 $$ \begin{align} \Delta_{E_{0},\chi}^{\sharp}\phi=\sum_{i=1}^{m}(\Delta_{E_{0}}\phi_{i})\otimes e_{i}, \end{align} $$
$$ \begin{align} \Delta_{E_{0},\chi}^{\sharp}\phi=\sum_{i=1}^{m}(\Delta_{E_{0}}\phi_{i})\otimes e_{i}, \end{align} $$
where
![]() $\Delta _{E_{0}}$
denotes the Bochner–Laplace operator
$\Delta _{E_{0}}$
denotes the Bochner–Laplace operator
![]() $\Delta ^{E_{0}}=(\nabla ^{E_{0}})^*\nabla ^{E_{0}}$
associated to the connection
$\Delta ^{E_{0}}=(\nabla ^{E_{0}})^*\nabla ^{E_{0}}$
associated to the connection
![]() $\nabla ^{E_{0}}$
. Let now
$\nabla ^{E_{0}}$
. Let now
![]() $\widetilde {E}_{0}, \widetilde {E}_{\chi }$
be the pullbacks to
$\widetilde {E}_{0}, \widetilde {E}_{\chi }$
be the pullbacks to
![]() $\widetilde {X}$
of
$\widetilde {X}$
of
![]() $E_{0},E_{\chi }$
, respectively. Then,
$E_{0},E_{\chi }$
, respectively. Then,
and
With respect to the isomorphism (8.3), it follows from Equation (8.2) that the lift of
![]() $\Delta _{E_{0},\chi }^{\sharp }$
to
$\Delta _{E_{0},\chi }^{\sharp }$
to
![]() $\widetilde {X}$
takes the form
$\widetilde {X}$
takes the form
where
![]() $\widetilde {\Delta }_{E_{0}}$
is the lift of
$\widetilde {\Delta }_{E_{0}}$
is the lift of
![]() $\Delta _{E_{0}}$
to
$\Delta _{E_{0}}$
to
![]() $\widetilde {X}$
. By Equation (8.2),
$\widetilde {X}$
. By Equation (8.2),
![]() $\Delta _{E_{0},\chi }^{\sharp }$
has principal symbol
$\Delta _{E_{0},\chi }^{\sharp }$
has principal symbol
Hence, it has nice spectral properties, that is, its spectrum is discrete and contained in a translate of a positive cone
![]() $C\subset \mathbb {C}$
such that
$C\subset \mathbb {C}$
such that
![]() $\mathbb {R}^{+}\subset C$
([Reference Spilioti48, Lemma 8.6]).
$\mathbb {R}^{+}\subset C$
([Reference Spilioti48, Lemma 8.6]).
We specialize now the twisted Bochner–Laplace operator
![]() $\Delta _{E_{0},\chi }^{\sharp }$
to the case of the operator
$\Delta _{E_{0},\chi }^{\sharp }$
to the case of the operator
![]() $\Delta ^{\sharp }_{\tau ,\chi }$
acting on smooth sections of the twisted vector bundle
$\Delta ^{\sharp }_{\tau ,\chi }$
acting on smooth sections of the twisted vector bundle
![]() $E_{\tau }\otimes E_{\chi }$
. Here,
$E_{\tau }\otimes E_{\chi }$
. Here,
![]() $E_{\tau }$
is the locally homogeneous vector bundle associated with a finite-dimensional, unitary representation
$E_{\tau }$
is the locally homogeneous vector bundle associated with a finite-dimensional, unitary representation
![]() $\tau $
of K. The keypoint is that when we consider the lift
$\tau $
of K. The keypoint is that when we consider the lift
![]() $\widetilde {\Delta }^{\sharp }_{\tau ,\chi }$
of the twisted Bochner–Laplace operator
$\widetilde {\Delta }^{\sharp }_{\tau ,\chi }$
of the twisted Bochner–Laplace operator
![]() $\Delta ^{\sharp }_{\tau ,\chi }$
to the universal covering
$\Delta ^{\sharp }_{\tau ,\chi }$
to the universal covering
![]() $\widetilde {X}$
, it acts as the identity operator on
$\widetilde {X}$
, it acts as the identity operator on
![]() $V_{\chi }$
. By Equation (8.1), we have
$V_{\chi }$
. By Equation (8.1), we have
where
![]() $\widetilde {\Delta }_\tau $
is the lift to
$\widetilde {\Delta }_\tau $
is the lift to
![]() $\widetilde {X}$
of the Bochner–Laplace operator
$\widetilde {X}$
of the Bochner–Laplace operator
![]() $\Delta _{\tau }$
, associated with the representation
$\Delta _{\tau }$
, associated with the representation
![]() $\tau $
of K.
$\tau $
of K.
8.2 The twisted operator
 $A_{\chi }^{\sharp }(\sigma )$
$A_{\chi }^{\sharp }(\sigma )$
In this section, we define the twisted operators
![]() $A_{\chi }^{\sharp }(\sigma )$
, associated with
$A_{\chi }^{\sharp }(\sigma )$
, associated with
![]() $\sigma \in \widehat {M}$
and representations
$\sigma \in \widehat {M}$
and representations
![]() $\chi $
of
$\chi $
of
![]() $\Gamma $
, acting on smooth sections of twisted vector bundles. These operators are first introduced in [Reference Bunke and Olbrich7]. For more details, we refer the reader to [Reference Spilioti48, Section 5].
$\Gamma $
, acting on smooth sections of twisted vector bundles. These operators are first introduced in [Reference Bunke and Olbrich7]. For more details, we refer the reader to [Reference Spilioti48, Section 5].
We define the restricted Weyl group as the quotient
![]() $ W_{A}:=M'/M$
. Recall from Section 7.1 that
$ W_{A}:=M'/M$
. Recall from Section 7.1 that
![]() $M'=\operatorname {\mathrm {Norm}}_{K}(A)$
is the normalizer of A in K. Then,
$M'=\operatorname {\mathrm {Norm}}_{K}(A)$
is the normalizer of A in K. Then,
![]() $W_{A}$
has order 2. Let
$W_{A}$
has order 2. Let
![]() $w\in W_{A}$
be the nontrivial element of
$w\in W_{A}$
be the nontrivial element of
![]() $W_{A}$
, and
$W_{A}$
, and
![]() $m_{w}$
a representative of w in
$m_{w}$
a representative of w in
![]() $M'$
. The action of
$M'$
. The action of
![]() $W_{A}$
on
$W_{A}$
on
![]() $\widehat {M}$
is defined by
$\widehat {M}$
is defined by
![]() $(w\sigma )(m):=\sigma (m_{w}^{-1}mm_{w})$
,
$(w\sigma )(m):=\sigma (m_{w}^{-1}mm_{w})$
,
![]() $m\in M, \sigma \in \widehat {M}$
. Following the proof of Proposition 1.1 in [Reference Bunke and Olbrich7] (see also [Reference Pfaff39, Proposition 2.3]), there exist unique integers
$m\in M, \sigma \in \widehat {M}$
. Following the proof of Proposition 1.1 in [Reference Bunke and Olbrich7] (see also [Reference Pfaff39, Proposition 2.3]), there exist unique integers
![]() $m_{\tau }(\sigma )\in \{-1,0,1\}$
, which are equal to zero except for finitely many
$m_{\tau }(\sigma )\in \{-1,0,1\}$
, which are equal to zero except for finitely many
![]() $\tau \in \widehat {K}$
such that there exist unique integers
$\tau \in \widehat {K}$
such that there exist unique integers
![]() $m_{\tau }(\sigma )\in \{-1,0,1\}$
, which are equal to zero except for finitely many
$m_{\tau }(\sigma )\in \{-1,0,1\}$
, which are equal to zero except for finitely many
![]() $\tau \in \widehat {K}$
such that
$\tau \in \widehat {K}$
such that
-
• if
 $\sigma $
is Weyl invariant,
$\sigma $
is Weyl invariant,
 $ \sigma =\sum _{\tau \in \widehat {K}}m_{\tau }(\sigma )i^{*}(\tau ); $
$ \sigma =\sum _{\tau \in \widehat {K}}m_{\tau }(\sigma )i^{*}(\tau ); $
-
• if
 $\sigma $
is non-Weyl invariant,
$\sigma $
is non-Weyl invariant,
 $ \sigma +w\sigma =\sum _{\tau \in \widehat {K}}m_{\tau }(\sigma )i^{*}(\tau ). $
$ \sigma +w\sigma =\sum _{\tau \in \widehat {K}}m_{\tau }(\sigma )i^{*}(\tau ). $
We define a locally homogeneous vector bundle
![]() $E(\sigma )$
associated to
$E(\sigma )$
associated to
![]() $\sigma $
by
$\sigma $
by
 $$ \begin{align*} E(\sigma):=\bigoplus_{\substack{\tau\in\widehat{K}\\m_{\tau}(\sigma)\neq 0}}E_{\tau}, \end{align*} $$
$$ \begin{align*} E(\sigma):=\bigoplus_{\substack{\tau\in\widehat{K}\\m_{\tau}(\sigma)\neq 0}}E_{\tau}, \end{align*} $$
where
![]() $E_{\tau }$
is the locally homogeneous vector bundle associated with
$E_{\tau }$
is the locally homogeneous vector bundle associated with
![]() $\tau \in \widehat {K}$
. The vector bundle
$\tau \in \widehat {K}$
. The vector bundle
![]() $E(\sigma )$
has a grading
$E(\sigma )$
has a grading
This grading is defined exactly by the positive or negative sign of
![]() $m_{\tau }(\sigma )$
. Let
$m_{\tau }(\sigma )$
. Let
![]() $\widetilde {E}(\sigma )$
be the pullback of
$\widetilde {E}(\sigma )$
be the pullback of
![]() $E(\sigma )$
to
$E(\sigma )$
to
![]() $\widetilde {X}$
. Then,
$\widetilde {X}$
. Then,
 $$ \begin{align*} \widetilde{E}(\sigma)=\bigoplus_{\substack{\tau\in\widehat{K}\\ m_{\tau}(\sigma)\neq0}}\widetilde{E}_{\tau}. \end{align*} $$
$$ \begin{align*} \widetilde{E}(\sigma)=\bigoplus_{\substack{\tau\in\widehat{K}\\ m_{\tau}(\sigma)\neq0}}\widetilde{E}_{\tau}. \end{align*} $$
We assume now that
![]() $\tau \in \widehat {K}$
is irreducible. Recall that
$\tau \in \widehat {K}$
is irreducible. Recall that
![]() $ \widetilde {\Delta }_{\tau }=-R(\Omega )+\lambda _{\tau }\operatorname {\mathrm {Id}}. $
([Reference Miatello29, Proposition 1.1], see also [Reference Spilioti48, (5.4)]) We put
$ \widetilde {\Delta }_{\tau }=-R(\Omega )+\lambda _{\tau }\operatorname {\mathrm {Id}}. $
([Reference Miatello29, Proposition 1.1], see also [Reference Spilioti48, (5.4)]) We put
Hence, the operator
![]() $\widetilde {A}_{\tau }$
acts like
$\widetilde {A}_{\tau }$
acts like
![]() $-R(\Omega )$
on the space of smooth sections of
$-R(\Omega )$
on the space of smooth sections of
![]() $\widetilde {E}_{\tau }$
. It is an elliptic, formally self-adjoint operator of second order. By [Reference Chernoof12], it is an essentially self-adjoint operator. Its self-adjoint extension will be also denoted by
$\widetilde {E}_{\tau }$
. It is an elliptic, formally self-adjoint operator of second order. By [Reference Chernoof12], it is an essentially self-adjoint operator. Its self-adjoint extension will be also denoted by
![]() $\widetilde {A}_{\tau }$
. We get then the operator
$\widetilde {A}_{\tau }$
. We get then the operator
![]() $\widetilde {A}^{\sharp }_{\tau ,\chi }$
acting on the space
$\widetilde {A}^{\sharp }_{\tau ,\chi }$
acting on the space
![]() $C^{\infty }(\widetilde {X},\widetilde {E}_{\tau }\otimes \widetilde {E}_{\chi })$
, defined by
$C^{\infty }(\widetilde {X},\widetilde {E}_{\tau }\otimes \widetilde {E}_{\chi })$
, defined by
We put
where
![]() $\nu _{\sigma }$
is as in Equations (7.5) and
$\nu _{\sigma }$
is as in Equations (7.5) and
![]() $\rho ,\rho _{m}$
are defined by Equations (7.3) and (7.4), respectively. We define the operator
$\rho ,\rho _{m}$
are defined by Equations (7.3) and (7.4), respectively. We define the operator
![]() $A_{\chi }^{\sharp }(\sigma )$
acting on
$A_{\chi }^{\sharp }(\sigma )$
acting on
![]() $C^{\infty }(X,E(\sigma )\otimes E_{\chi })$
by
$C^{\infty }(X,E(\sigma )\otimes E_{\chi })$
by
 $$ \begin{align} A_{\chi}^{\sharp}(\sigma):=\bigoplus_{m_{\tau}(\sigma)\neq 0}A_{\tau,\chi}^{\sharp}+c(\sigma). \end{align} $$
$$ \begin{align} A_{\chi}^{\sharp}(\sigma):=\bigoplus_{m_{\tau}(\sigma)\neq 0}A_{\tau,\chi}^{\sharp}+c(\sigma). \end{align} $$
The operator
![]() $A_{\chi }^{\sharp }(\sigma )$
preserves the grading and it is a non-self-adjoint, elliptic operator of order two.
$A_{\chi }^{\sharp }(\sigma )$
preserves the grading and it is a non-self-adjoint, elliptic operator of order two.
9 The determinant formula
In [Reference Spilioti49], a determinant formula has been proved, which gives an interpretation of the twisted Ruelle zeta function in terms of graded, regularized determinants of twisted, non-self-adjoint, elliptic differential operators. We recall here some facts and definitions from [Reference Spilioti49].
Let
![]() $\sigma _{p}$
be the standard representation of M in
$\sigma _{p}$
be the standard representation of M in
![]() $\Lambda ^{p}\mathbb {R}^{d-1}\otimes \mathbb {C}$
. Let
$\Lambda ^{p}\mathbb {R}^{d-1}\otimes \mathbb {C}$
. Let
![]() $\sigma ,\sigma '\in \widehat {M}$
. We denote by
$\sigma ,\sigma '\in \widehat {M}$
. We denote by
![]() $[\sigma _{p}\otimes \sigma :\sigma ']$
the multiplicity of
$[\sigma _{p}\otimes \sigma :\sigma ']$
the multiplicity of
![]() $\sigma '$
in
$\sigma '$
in
![]() $\sigma _{p}\otimes \sigma $
. We distinguish again two cases for
$\sigma _{p}\otimes \sigma $
. We distinguish again two cases for
![]() $\sigma '\in \widehat {M}$
.
$\sigma '\in \widehat {M}$
.
-
• case (a):
 $\sigma '$
is invariant under the action of the restricted Weyl group
$\sigma '$
is invariant under the action of the restricted Weyl group
 $W_{A}$
. Then,
$W_{A}$
. Then,
 $i^{*}(\tau )=\sigma '$
, where
$i^{*}(\tau )=\sigma '$
, where
 $\tau \in R(K)$
.
$\tau \in R(K)$
. -
• case (b):
 $\sigma '$
is not invariant under the action of the restricted Weyl group
$\sigma '$
is not invariant under the action of the restricted Weyl group
 $W_{A}$
. Then,
$W_{A}$
. Then,
 $i^{*}(\tau )=\sigma '+w\sigma '$
, where
$i^{*}(\tau )=\sigma '+w\sigma '$
, where
 $\tau \in R(K)$
.
$\tau \in R(K)$
.
We define the operator
 $$ \begin{align} A_{\chi}^{\sharp}(\sigma_{p}\otimes\sigma):=\bigoplus_{[\sigma']\in\widehat{M}/W_{A}}\bigoplus_{i=1}^{[\sigma_{p}\otimes\sigma:\sigma']}A^{\sharp}_{\chi}(\sigma'), \end{align} $$
$$ \begin{align} A_{\chi}^{\sharp}(\sigma_{p}\otimes\sigma):=\bigoplus_{[\sigma']\in\widehat{M}/W_{A}}\bigoplus_{i=1}^{[\sigma_{p}\otimes\sigma:\sigma']}A^{\sharp}_{\chi}(\sigma'), \end{align} $$
acting on the space
![]() $C^{\infty }(X,E(\sigma ')\otimes E_{\chi })$
, where
$C^{\infty }(X,E(\sigma ')\otimes E_{\chi })$
, where
![]() $E(\sigma ')$
is the vector bundle over X, constructed as in [Reference Spilioti48, p. 175].
$E(\sigma ')$
is the vector bundle over X, constructed as in [Reference Spilioti48, p. 175].
Let
![]() $\alpha $
be the unique positive root of
$\alpha $
be the unique positive root of
![]() $(\mathfrak {g},\mathfrak {a})$
. Let
$(\mathfrak {g},\mathfrak {a})$
. Let
![]() $H\in \mathfrak {a}$
such that
$H\in \mathfrak {a}$
such that
![]() $\alpha (H)=1$
. The character
$\alpha (H)=1$
. The character
![]() $\lambda \equiv \lambda _{p}$
of A is defined by
$\lambda \equiv \lambda _{p}$
of A is defined by
![]() $\lambda \equiv \lambda _{p}(a)=e^{p\alpha (\log a)}$
. Then, we can identify
$\lambda \equiv \lambda _{p}(a)=e^{p\alpha (\log a)}$
. Then, we can identify
![]() $\lambda $
with p. By [Reference Spilioti49, Proposition 7.9, case (a)], we have the following proposition.
$\lambda $
with p. By [Reference Spilioti49, Proposition 7.9, case (a)], we have the following proposition.
Proposition 9.1. The Ruelle zeta function has the representation
 $$ \begin{align} R(s;\sigma,\chi)=\notag&\prod_{p=0}^{d-1}{{\det}_{\operatorname{\mathrm{gr}}}(A^{\sharp}_{\chi}(\sigma_{p}\otimes\sigma)+(s+\vert\rho\vert-p)^{2})}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim(V_{\sigma})\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg). \end{align} $$
$$ \begin{align} R(s;\sigma,\chi)=\notag&\prod_{p=0}^{d-1}{{\det}_{\operatorname{\mathrm{gr}}}(A^{\sharp}_{\chi}(\sigma_{p}\otimes\sigma)+(s+\vert\rho\vert-p)^{2})}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim(V_{\sigma})\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg). \end{align} $$
Remark 9.2. In the determinant formula (9.2), the regularized determinants are graded, with respect to the grading (8.5) of the locally homogeneous vector bundle
![]() $E(\sigma )$
over X.
$E(\sigma )$
over X.
Theorem 9.3. The Ruelle zeta function has the representation
 $$ \begin{align} R(s;\chi)=\notag&\prod_{k=0}^{d-1}\prod_{p=k}^{d-1}{\det\big(\Delta^{\sharp}_{\chi,k}+s(s+2(\vert\rho\vert-p))\big)}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg). \end{align} $$
$$ \begin{align} R(s;\chi)=\notag&\prod_{k=0}^{d-1}\prod_{p=k}^{d-1}{\det\big(\Delta^{\sharp}_{\chi,k}+s(s+2(\vert\rho\vert-p))\big)}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg). \end{align} $$
Let
![]() $d_{\chi ,k}:=\dim \operatorname {\mathrm {Ker}}(\Delta _{\chi ,k})$
. Then, the singularity of the Ruelle zeta function at
$d_{\chi ,k}:=\dim \operatorname {\mathrm {Ker}}(\Delta _{\chi ,k})$
. Then, the singularity of the Ruelle zeta function at
![]() $s=0$
is of order
$s=0$
is of order
 $$ \begin{align} \sum_{k=0}^{(d-1)/2}(d+1-2k)(-1)^{k}d_{\chi,k}. \end{align} $$
$$ \begin{align} \sum_{k=0}^{(d-1)/2}(d+1-2k)(-1)^{k}d_{\chi,k}. \end{align} $$
Proof. We denote by
![]() $r_{p}$
be the p-th exterior power of the standard representation of K. This notation coincides with the notation used in [Reference Bunke and Olbrich7, p. 23–24]. Then, for
$r_{p}$
be the p-th exterior power of the standard representation of K. This notation coincides with the notation used in [Reference Bunke and Olbrich7, p. 23–24]. Then, for
![]() $p=0,\ldots , d-1$
, we have
$p=0,\ldots , d-1$
, we have
![]() $i^{*}(r_{p})=\sigma _{p}+\sigma _{p-1}$
. Let
$i^{*}(r_{p})=\sigma _{p}+\sigma _{p-1}$
. Let
![]() $k_{p}\in R(K)$
, defined by
$k_{p}\in R(K)$
, defined by
 $$ \begin{align*} k_{p}:=\sum_{k=0}^{p}(-1)^{k}r_{p-k}. \end{align*} $$
$$ \begin{align*} k_{p}:=\sum_{k=0}^{p}(-1)^{k}r_{p-k}. \end{align*} $$
Then, for
![]() $p=0,1,\ldots , d-1$
, one has
$p=0,1,\ldots , d-1$
, one has
![]() $\sigma _{p}=i^{*}(k_{p})$
. Let
$\sigma _{p}=i^{*}(k_{p})$
. Let
![]() $E_{k_{p}}$
,
$E_{k_{p}}$
,
![]() $E_{r_{k}}$
be the locally homogeneous vector bundles over X, associated with
$E_{r_{k}}$
be the locally homogeneous vector bundles over X, associated with
![]() $k_{p}$
and
$k_{p}$
and
![]() $r_{k}$
, correspondingly. We consider
$r_{k}$
, correspondingly. We consider
![]() $\sigma $
being trivial. By Equation (8.6),
$\sigma $
being trivial. By Equation (8.6),
![]() $c(\sigma _{p})=(\vert \rho \vert -p)^{2}$
. By Equations (8.7) and (9.1), the operators
$c(\sigma _{p})=(\vert \rho \vert -p)^{2}$
. By Equations (8.7) and (9.1), the operators
![]() $A^{\sharp }_{\chi }(\sigma _{p})+(\vert \rho \vert -p)^{2}$
and
$A^{\sharp }_{\chi }(\sigma _{p})+(\vert \rho \vert -p)^{2}$
and
![]() $-R(\Omega )$
on
$-R(\Omega )$
on
![]() $C^{\infty }(X, E_{k_{p}}\otimes V_{\chi } )$
coincide. On the other hand, by Kuga’s lemma (Subsection 2.1.3), the Casimir operator
$C^{\infty }(X, E_{k_{p}}\otimes V_{\chi } )$
coincide. On the other hand, by Kuga’s lemma (Subsection 2.1.3), the Casimir operator
![]() $R(\Omega )$
acts as the negative Hodge Laplacian
$R(\Omega )$
acts as the negative Hodge Laplacian
![]() $-\Delta ^{\sharp }_{\chi ,k}$
on
$-\Delta ^{\sharp }_{\chi ,k}$
on
![]() $C^{\infty }(X, E_{r_{k}}\otimes V_{\chi })$
. Hence, by Equation (9.2), we get
$C^{\infty }(X, E_{r_{k}}\otimes V_{\chi })$
. Hence, by Equation (9.2), we get
 $$ \begin{align*} R(s;\chi)=\prod_{p=0}^{d-1}&{{\det}_{\operatorname{\mathrm{gr}}}(A^{\sharp}_{\chi}(\sigma_{p})+(s+\vert\rho\vert-p)^{2})}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg)\\ =\prod_{k=0}^{d-1}&\prod_{p=k}^{d-1}{\det\big(\Delta^{\sharp}_{\chi,k}+s(s+2(\vert\rho\vert-p))\big)}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg). \end{align*} $$
$$ \begin{align*} R(s;\chi)=\prod_{p=0}^{d-1}&{{\det}_{\operatorname{\mathrm{gr}}}(A^{\sharp}_{\chi}(\sigma_{p})+(s+\vert\rho\vert-p)^{2})}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg)\\ =\prod_{k=0}^{d-1}&\prod_{p=k}^{d-1}{\det\big(\Delta^{\sharp}_{\chi,k}+s(s+2(\vert\rho\vert-p))\big)}^{(-1)^{p}}\\ &\cdot\exp\bigg((-1)^{\frac{d-1}{2}+1}\pi(d+1)\dim (V_{\chi})\frac{\operatorname{\mathrm{Vol}}(X)}{\operatorname{\mathrm{Vol}}(S^{d})}s\bigg). \end{align*} $$
For the order of the singularity of the Ruelle zeta function at
![]() $s=0$
, Equation (9.4) follows from Poincaré duality on differential forms.
$s=0$
, Equation (9.4) follows from Poincaré duality on differential forms.
Remark 9.4. We note here that for
![]() $p=\frac {d-1}{2}$
,
$p=\frac {d-1}{2}$
,
![]() $\sigma _{p}$
is not irreducible. In fact,
$\sigma _{p}$
is not irreducible. In fact,
![]() $\sigma _{\frac {d-1}{2}}$
decomposes into
$\sigma _{\frac {d-1}{2}}$
decomposes into
![]() $\sigma _{+}+\sigma _{-}$
, and
$\sigma _{+}+\sigma _{-}$
, and
![]() $\sigma _{\pm }=w\sigma _{\mp }$
. Then, we use Equation (9.1) to define
$\sigma _{\pm }=w\sigma _{\mp }$
. Then, we use Equation (9.1) to define
![]() $A^{\sharp }_{\chi }(\sigma _{\frac {d-1}{2}})$
. By [Reference Millson30, Lemma 1.4],
$A^{\sharp }_{\chi }(\sigma _{\frac {d-1}{2}})$
. By [Reference Millson30, Lemma 1.4],
![]() $c(\sigma _{+})=c(\sigma _{-})=0$
.
$c(\sigma _{+})=c(\sigma _{-})=0$
.
Remark 9.5. In the case of unitary representations, which are acyclic, we can obtain the triviality of the kernels of the Hodge Laplacian
![]() $\Delta _{\chi ,k}$
, since by Hodge theorem we have
$\Delta _{\chi ,k}$
, since by Hodge theorem we have
where
![]() $H^{k}(X,E_{\chi })$
is the cohomology with coefficients in the local system defined by
$H^{k}(X,E_{\chi })$
is the cohomology with coefficients in the local system defined by
![]() $\chi $
. In the present case, there is no such an isomorphism and one can find noninjective Laplacians associated with acyclic representations of
$\chi $
. In the present case, there is no such an isomorphism and one can find noninjective Laplacians associated with acyclic representations of
![]() $\Gamma $
.
$\Gamma $
.
10 Ruelle zeta function and refined analytic torsion
This section is the key part of the article since all the objects studied before get identified with each others.
Let V be as in Subsection 3.3, that is, V is an open neighbourhood of the set
![]() $\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
of acyclic and unitary representations of
$\operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
of acyclic and unitary representations of
![]() $\pi _{1}(X)=\Gamma $
such that, for all
$\pi _{1}(X)=\Gamma $
such that, for all
![]() $\chi \in V$
,
$\chi \in V$
,
![]() $B_{\chi }$
is bijective. Then, we have the following theorem.
$B_{\chi }$
is bijective. Then, we have the following theorem.
Theorem 10.1. Let
![]() $\chi \in V$
. Then, the Ruelle zeta function
$\chi \in V$
. Then, the Ruelle zeta function
![]() $R(s;\chi )$
is regular at
$R(s;\chi )$
is regular at
![]() $s=0$
and is equal to the complex Cappell-Miller torsion,
$s=0$
and is equal to the complex Cappell-Miller torsion,
Proof. For
![]() $\chi \in V$
, the operator
$\chi \in V$
, the operator
![]() $B_{\chi ,k}^{2}$
coincides with the flat Laplacian
$B_{\chi ,k}^{2}$
coincides with the flat Laplacian
![]() $\Delta ^{\sharp }_{\chi ,k}$
on
$\Delta ^{\sharp }_{\chi ,k}$
on
![]() $\Lambda ^{k}(X,E_{\chi })$
and it is injective. Hence, by Theorem 5.3, the Ruelle zeta function
$\Lambda ^{k}(X,E_{\chi })$
and it is injective. Hence, by Theorem 5.3, the Ruelle zeta function
![]() $R(s;\chi )$
is regular at zero and in addition, by Equation (9.3),
$R(s;\chi )$
is regular at zero and in addition, by Equation (9.3),
 $$ \begin{align} R(0;\chi)=\prod_{k=0}^{d-1}{\det(\Delta^{\sharp}_{\chi,k})}^{(d-k)(-1)^{k}} = \prod_{k=1}^{d}{\det(\Delta^{\sharp}_{\chi,k})}^{k(-1)^{k-1}}. \end{align} $$
$$ \begin{align} R(0;\chi)=\prod_{k=0}^{d-1}{\det(\Delta^{\sharp}_{\chi,k})}^{(d-k)(-1)^{k}} = \prod_{k=1}^{d}{\det(\Delta^{\sharp}_{\chi,k})}^{k(-1)^{k-1}}. \end{align} $$
Hence, Equation (10.1) follows by Equations (6.2) and (10.2).
Corollary 10.2. Let
![]() $\chi \in V$
. Then the Ruelle zeta function
$\chi \in V$
. Then the Ruelle zeta function
![]() $R(s;\chi )$
is regular at
$R(s;\chi )$
is regular at
![]() $s=0$
and is related to the refined analytic torsion
$s=0$
and is related to the refined analytic torsion
![]() $T_{\chi }$
by
$T_{\chi }$
by
Let now
![]() $\chi \in \operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
. Then, by [Reference Bunke and Olbrich7, Theorem 4.8], the Ruelle zeta function
$\chi \in \operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
. Then, by [Reference Bunke and Olbrich7, Theorem 4.8], the Ruelle zeta function
![]() $R(s,\chi )$
associated with
$R(s,\chi )$
associated with
![]() $\chi $
is regular at
$\chi $
is regular at
![]() $s=0$
. Moreover, the Cappell–Miller torsion coincides with the square of the Ray–Singer real-valued torsion
$s=0$
. Moreover, the Cappell–Miller torsion coincides with the square of the Ray–Singer real-valued torsion
![]() $T^{RS}_{\chi }$
. On the other hand, in this case, the refined analytic torsion is still a complex number, given by
$T^{RS}_{\chi }$
. On the other hand, in this case, the refined analytic torsion is still a complex number, given by
Here, we denote
![]() $\xi _{\chi }=\xi (\chi , g, \theta )$
. If
$\xi _{\chi }=\xi (\chi , g, \theta )$
. If
![]() $\chi $
is unitary and acyclic, the term
$\chi $
is unitary and acyclic, the term
![]() $e^{\xi _{\chi }}$
coincides with the Ray–Singer torsion
$e^{\xi _{\chi }}$
coincides with the Ray–Singer torsion
![]() $T^{RS}_{\chi }$
, and the eta invariant
$T^{RS}_{\chi }$
, and the eta invariant
![]() $\eta (\chi ,g)$
is real valued. Hence,
$\eta (\chi ,g)$
is real valued. Hence,
Therefore, Equations (10.1), (10.3) and (10.4) yield the following classical result (see [Reference Bunke and Olbrich7, Theorem 4.8]).
Corollary 10.3. Let
![]() $\chi \in \operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
. Then, the Ruelle zeta function
$\chi \in \operatorname {\mathrm {Rep}}^{u}_{0}(\pi _{1}(X),\mathbb {C}^{n})$
. Then, the Ruelle zeta function
![]() $R(s;\chi )$
associated with
$R(s;\chi )$
associated with
![]() $\chi $
is regular at
$\chi $
is regular at
![]() $s=0$
and
$s=0$
and
Corollary 10.4. Let
![]() $\chi \in V$
. Then, the Ruelle zeta function
$\chi \in V$
. Then, the Ruelle zeta function
![]() $R(s;\chi )$
is regular at
$R(s;\chi )$
is regular at
![]() $s=0$
and
$s=0$
and
Proof. By [Reference Braverman and Kappeler6, Theorem 8.2], we have
Hence, Equation (10.5) follows from Equations (10.1), (10.3) and (10.6).
Using the alternative definition of the refined analytic torsion as in Section 8, we obtain the following corollary.
Corollary 10.5. Let
![]() $\chi \in V$
and
$\chi \in V$
and
![]() $n=4k$
,
$n=4k$
,
![]() $k\in \mathbb {Z}$
. Then, the Ruelle zeta function
$k\in \mathbb {Z}$
. Then, the Ruelle zeta function
![]() $R(s;\chi )$
is regular at
$R(s;\chi )$
is regular at
![]() $s=0$
and
$s=0$
and
11 Appendix: Refined analytic torsion as an element of the determinant line
For a general nonunitary representation, the definition of the refined analytic torsion differs from 4.1.1 and is not a complex number any more. It is an element of the determinant line of the cohomology. We recall here the definition from [Reference Braverman and Kappeler4]. Let
![]() $\mathbf {k}$
be a field of characteristic zero. Let V be a
$\mathbf {k}$
be a field of characteristic zero. Let V be a
![]() $\mathbf {k}$
-vector space of dimension n. We define the determinant line of V by
$\mathbf {k}$
-vector space of dimension n. We define the determinant line of V by
![]() $\det (V^{*}):=\Lambda ^{n}V$
, where
$\det (V^{*}):=\Lambda ^{n}V$
, where
![]() $\Lambda ^{n}V$
denotes the n-th exterior power of V. We set
$\Lambda ^{n}V$
denotes the n-th exterior power of V. We set
![]() $\det (0):=\mathbf {k}$
. If L is a
$\det (0):=\mathbf {k}$
. If L is a
![]() $\mathbf {k}$
-line (one-dimensional vector space), we define the dual line
$\mathbf {k}$
-line (one-dimensional vector space), we define the dual line
![]() $L^{-1}$
by
$L^{-1}$
by
![]() $L^{-1}:=\text {Hom}_{\mathbf {k}}(L,\mathbf {k})$
. For
$L^{-1}:=\text {Hom}_{\mathbf {k}}(L,\mathbf {k})$
. For
![]() $l\in L$
, we denote by
$l\in L$
, we denote by
![]() $l^{-1}\in L^{-1}$
the unique
$l^{-1}\in L^{-1}$
the unique
![]() $\mathbf {k}$
-linear map
$\mathbf {k}$
-linear map
![]() $L\rightarrow \mathbf {k}$
such that
$L\rightarrow \mathbf {k}$
such that
![]() $l^{-1}(l)=1$
. For a graded
$l^{-1}(l)=1$
. For a graded
![]() $\mathbf {k}$
-vector space
$\mathbf {k}$
-vector space
![]() $V^{*}=V^{0}\oplus V^{1} \cdots \oplus V^{d}$
, we define
$V^{*}=V^{0}\oplus V^{1} \cdots \oplus V^{d}$
, we define
 $$ \begin{align*} \det (V^{*}):= \bigotimes_{j=0}^{d}\det(V^{j})^{(-1)^{j}}. \end{align*} $$
$$ \begin{align*} \det (V^{*}):= \bigotimes_{j=0}^{d}\det(V^{j})^{(-1)^{j}}. \end{align*} $$
Let
![]() $(C^{*},\partial )$
,
$(C^{*},\partial )$
,
be a complex of finite-dimensional
![]() $\mathbf {k}$
-vector spaces. We call the integer d the length of the complex
$\mathbf {k}$
-vector spaces. We call the integer d the length of the complex
![]() $(C^{*},\partial )$
. We denote by
$(C^{*},\partial )$
. We denote by
 $$ \begin{align*} H^{*}(\partial)=\bigoplus_{i=0}^{d}H^{i}(\partial) \end{align*} $$
$$ \begin{align*} H^{*}(\partial)=\bigoplus_{i=0}^{d}H^{i}(\partial) \end{align*} $$
the cohomology of
![]() $(C^{*},\partial )$
. We set
$(C^{*},\partial )$
. We set
 $$ \begin{align*} &\det (C^{*}):= \bigotimes_{j=0}^{d}\det(C^{j})^{(-1)^{j}}\\ &\det (H^{*}):= \bigotimes_{j=0}^{d}\det(H^{j}(\partial))^{(-1)^{j}}. \end{align*} $$
$$ \begin{align*} &\det (C^{*}):= \bigotimes_{j=0}^{d}\det(C^{j})^{(-1)^{j}}\\ &\det (H^{*}):= \bigotimes_{j=0}^{d}\det(H^{j}(\partial))^{(-1)^{j}}. \end{align*} $$
We want to consider the determinant line of a direct sum of two (or more) finite-dimensional
![]() $\mathbf {k}$
-vector spaces. Let
$\mathbf {k}$
-vector spaces. Let
![]() $V,W$
be finite-dimensional
$V,W$
be finite-dimensional
![]() $\mathbf {k}$
-vector spaces of dimension
$\mathbf {k}$
-vector spaces of dimension
![]() $\dim V=k$
and
$\dim V=k$
and
![]() $\dim W=l$
, correspondingly. We define the canonical fusion isomorphism
$\dim W=l$
, correspondingly. We define the canonical fusion isomorphism
by
 $$ \begin{align*} \mu_{V,W}\colon (v_{1}\wedge v_{2}\wedge\ldots\wedge v_{k})\otimes (w_{1}&\wedge w_{2}\wedge\ldots\wedge w_{l})\\ &\mapsto v_{1}\wedge v_{2}\wedge\ldots\wedge v_{k}\wedge w_{1}\wedge w_{2}\wedge\ldots\wedge w_{l}, \end{align*} $$
$$ \begin{align*} \mu_{V,W}\colon (v_{1}\wedge v_{2}\wedge\ldots\wedge v_{k})\otimes (w_{1}&\wedge w_{2}\wedge\ldots\wedge w_{l})\\ &\mapsto v_{1}\wedge v_{2}\wedge\ldots\wedge v_{k}\wedge w_{1}\wedge w_{2}\wedge\ldots\wedge w_{l}, \end{align*} $$
where
![]() $v_{i}\in V$
and
$v_{i}\in V$
and
![]() $w_{j}\in W$
. For
$w_{j}\in W$
. For
![]() $v\in \det (V)$
and
$v\in \det (V)$
and
![]() $w\in \det (W)$
, we have
$w\in \det (W)$
, we have
We denote by
the transpose of the inverse of
![]() $\mu _{V,W}$
. Then, it follows that for
$\mu _{V,W}$
. Then, it follows that for
![]() $v\in \det (V)$
and
$v\in \det (V)$
and
![]() $w\in \det (W)$
$w\in \det (W)$
Let now
![]() $V_{1},\ldots V_{r}$
, finite-dimensional
$V_{1},\ldots V_{r}$
, finite-dimensional
![]() $\mathbf {k}$
-vector spaces. We define an isomorphism
$\mathbf {k}$
-vector spaces. We define an isomorphism
For
![]() $j=1,\ldots , r-1$
, it holds
$j=1,\ldots , r-1$
, it holds
We fix now a direct sum decomposition
such that
![]() $B^{j}\oplus H^{j}=\operatorname {\mathrm {Ker}}(\partial )\cap C^{j}$
and
$B^{j}\oplus H^{j}=\operatorname {\mathrm {Ker}}(\partial )\cap C^{j}$
and
![]() $B^{j}=\partial (C^{j-1})=\partial (A^{j-1)})$
, for all j. Note that
$B^{j}=\partial (C^{j-1})=\partial (A^{j-1)})$
, for all j. Note that
![]() $A^{d}={0}$
. Set
$A^{d}={0}$
. Set
![]() $A^{-1}=\{0\}$
. Then,
$A^{-1}=\{0\}$
. Then,
![]() $H^{j}$
is naturally isomorphic to the cohomology
$H^{j}$
is naturally isomorphic to the cohomology
![]() $H^{j}(\partial )$
and
$H^{j}(\partial )$
and
![]() $\partial $
defines an isomorphism
$\partial $
defines an isomorphism
![]() $\partial \colon A^{j}\rightarrow B^{j+1}$
. For each
$\partial \colon A^{j}\rightarrow B^{j+1}$
. For each
![]() $j=0,\ldots ,d$
, we fix
$j=0,\ldots ,d$
, we fix
![]() $c_{j}\det (C^{j})$
and
$c_{j}\det (C^{j})$
and
![]() $a_{j}\in \det (A^{j})$
. Let
$a_{j}\in \det (A^{j})$
. Let
![]() $\partial (a_{j})\det (B^{j+1})$
be the image of
$\partial (a_{j})\det (B^{j+1})$
be the image of
![]() $a_{j}$
under the map
$a_{j}$
under the map
![]() $\det (A^{j})\rightarrow \det (B^{j+1})$
, induced by the isomorphism
$\det (A^{j})\rightarrow \det (B^{j+1})$
, induced by the isomorphism
![]() $\partial \colon A^{j}\rightarrow B^{j+1}$
. Then, for each
$\partial \colon A^{j}\rightarrow B^{j+1}$
. Then, for each
![]() $j=0,\cdots , d$
, there is a unique element
$j=0,\cdots , d$
, there is a unique element
![]() $h_{j}\det (H^{j})$
such that
$h_{j}\det (H^{j})$
such that
Let
![]() $\phi _{C^{*}}$
be the isomorphism
$\phi _{C^{*}}$
be the isomorphism
defined by
where
 $$ \begin{align*} \mathcal{N}(C^{*}):=\frac{1}{2}\sum_{j=0}^{d}\dim A^{j}(\dim A^{j} +(-1)^{j+1}). \end{align*} $$
$$ \begin{align*} \mathcal{N}(C^{*}):=\frac{1}{2}\sum_{j=0}^{d}\dim A^{j}(\dim A^{j} +(-1)^{j+1}). \end{align*} $$
Then,
![]() $\phi _{C^{*}}$
is independent of the choices of
$\phi _{C^{*}}$
is independent of the choices of
![]() $c_{j}$
and
$c_{j}$
and
![]() $a_{j}$
.
$a_{j}$
.
Remark 11.1. The isomorphism
![]() $\phi _{C^{*}}$
is a sign refinement of the standard construction by Milnor ([Reference Milnor31]). The sign factor
$\phi _{C^{*}}$
is a sign refinement of the standard construction by Milnor ([Reference Milnor31]). The sign factor
![]() $\mathcal {N}(C^{*})$
was introduced by Braverman and Kappeler in order to obtain various compatibility properties (see [Reference Braverman and Kappeler4, Remark 2.5, Lemma 2.7 and Proposition 5.6]).
$\mathcal {N}(C^{*})$
was introduced by Braverman and Kappeler in order to obtain various compatibility properties (see [Reference Braverman and Kappeler4, Remark 2.5, Lemma 2.7 and Proposition 5.6]).
11.1 Refined torsion of a finite-dimensional complex with a chirality operator
We consider now the chirality operator
![]() $\Gamma : C^{*}\rightarrow C^{*}$
such that
$\Gamma : C^{*}\rightarrow C^{*}$
such that
![]() $\Gamma : C^{j}\rightarrow C^{d-j}$
, for
$\Gamma : C^{j}\rightarrow C^{d-j}$
, for
![]() $j=0,\cdots ,d$
. For
$j=0,\cdots ,d$
. For
![]() $c_{j}\in \det (C^{j})$
,
$c_{j}\in \det (C^{j})$
,
![]() $\Gamma c_{j}\in \det (C^{d-j})$
is the image of
$\Gamma c_{j}\in \det (C^{d-j})$
is the image of
![]() $c_{j}$
under the isomorphism
$c_{j}$
under the isomorphism
![]() $\det (C^{j})\rightarrow \det (C^{d-j})$
, induced by
$\det (C^{j})\rightarrow \det (C^{d-j})$
, induced by
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $d=2r-1$
be an odd integer. We fix nonzero elements
$d=2r-1$
be an odd integer. We fix nonzero elements
![]() $c_{j}\in \det (C^{j})$
,
$c_{j}\in \det (C^{j})$
,
![]() $j=0,\cdots , r-1$
and consider the element
$j=0,\cdots , r-1$
and consider the element
 $$ \begin{align*} c_{\Gamma}:= (-1)^{\mathcal{R}(C^{*})}c_{0}\otimes & c_{1}^{-1}\otimes \cdots c_{r-1}^{(-1)^{r-1}}\\ &\otimes(\Gamma c_{r-1})^{(-1)^{r}} \otimes(\Gamma c_{r-2})^{(-1)^{r-1}} \otimes\cdots \otimes (\Gamma c_{0}^{-1})\notag \end{align*} $$
$$ \begin{align*} c_{\Gamma}:= (-1)^{\mathcal{R}(C^{*})}c_{0}\otimes & c_{1}^{-1}\otimes \cdots c_{r-1}^{(-1)^{r-1}}\\ &\otimes(\Gamma c_{r-1})^{(-1)^{r}} \otimes(\Gamma c_{r-2})^{(-1)^{r-1}} \otimes\cdots \otimes (\Gamma c_{0}^{-1})\notag \end{align*} $$
of
![]() $\det (C^{*})$
, where
$\det (C^{*})$
, where
 $$ \begin{align*} \mathcal{R}(C^{*})=\frac{1}{2}\sum_{j=0}^{r-1}\dim C^{j}(\dim C^{j}+(-1)^{r+j}). \end{align*} $$
$$ \begin{align*} \mathcal{R}(C^{*})=\frac{1}{2}\sum_{j=0}^{r-1}\dim C^{j}(\dim C^{j}+(-1)^{r+j}). \end{align*} $$
It follows from the definition of
![]() $c_{j}^{-1}$
that
$c_{j}^{-1}$
that
![]() $c_{\Gamma }$
is independent of the choice of
$c_{\Gamma }$
is independent of the choice of
![]() $c_{j}$
,
$c_{j}$
,
![]() $j=0,\ldots ,r-1$
.
$j=0,\ldots ,r-1$
.
Definition 11.1.1. We define the refined torsion
![]() $\rho _{\Gamma }$
of the pair
$\rho _{\Gamma }$
of the pair
![]() $(C^{*},\Gamma )$
by
$(C^{*},\Gamma )$
by
where
![]() $\phi _{C^{*}}$
is as in Equation (11.1).
$\phi _{C^{*}}$
is as in Equation (11.1).
We consider now the finite-dimensional analogue of the odd signature operator B, defined in a Riemannian manifold-setting by Equation (3.1). Let
![]() $B\colon C^{*}\rightarrow C^{*}$
be the signature operator, defined by
$B\colon C^{*}\rightarrow C^{*}$
be the signature operator, defined by
We consider its square,
![]() $B^{2}=(\partial \Gamma )^{2}+(\Gamma \partial )^{2}$
. Let
$B^{2}=(\partial \Gamma )^{2}+(\Gamma \partial )^{2}$
. Let
![]() $I\subset [0,\infty )$
. Let
$I\subset [0,\infty )$
. Let
![]() $C^{j}_{I}\subset C^{j}$
be the span of the generalized eigenvectors of the restriction of
$C^{j}_{I}\subset C^{j}$
be the span of the generalized eigenvectors of the restriction of
![]() $B^{2}$
to
$B^{2}$
to
![]() $C^{j}$
, corresponding to eigenvalues r with
$C^{j}$
, corresponding to eigenvalues r with
![]() $\vert r \vert \in I$
. Both
$\vert r \vert \in I$
. Both
![]() $\Gamma $
and
$\Gamma $
and
![]() $\partial $
commute with B and hence with
$\partial $
commute with B and hence with
![]() $B^{2}$
. Then, we have
$B^{2}$
. Then, we have
![]() $\Gamma :C^{j}_{I}\rightarrow C^{d-j}_{I}$
, and
$\Gamma :C^{j}_{I}\rightarrow C^{d-j}_{I}$
, and
![]() $\partial : C^{j}_{I}\rightarrow C^{j+1}_{I}$
. Hence, we obtain a subcomplex
$\partial : C^{j}_{I}\rightarrow C^{j+1}_{I}$
. Hence, we obtain a subcomplex
![]() $C_{I}^{*}$
of
$C_{I}^{*}$
of
![]() $C^{*}$
and the restriction
$C^{*}$
and the restriction
![]() $\Gamma _{I}$
of
$\Gamma _{I}$
of
![]() $\Gamma $
to
$\Gamma $
to
![]() $C_{I}^{*}$
is the chirality operator on this complex. Let
$C_{I}^{*}$
is the chirality operator on this complex. Let
![]() $\partial _{I}, B_{I}, B^{\operatorname {\mathrm {even}}}_{I}$
be the restriction to
$\partial _{I}, B_{I}, B^{\operatorname {\mathrm {even}}}_{I}$
be the restriction to
![]() $C_{I}^{*}$
of
$C_{I}^{*}$
of
![]() $\partial , B, B^{\operatorname {\mathrm {even}}}$
, correspondingly. Here, we denote
$\partial , B, B^{\operatorname {\mathrm {even}}}$
, correspondingly. Here, we denote
![]() $ B^{\operatorname {\mathrm {even}}}\colon C^{\operatorname {\mathrm {even}}}\rightarrow C^{\operatorname {\mathrm {even}}}$
, where
$ B^{\operatorname {\mathrm {even}}}\colon C^{\operatorname {\mathrm {even}}}\rightarrow C^{\operatorname {\mathrm {even}}}$
, where
![]() $C^{\operatorname {\mathrm {even}}}:=\bigoplus _{j \operatorname {\mathrm {even}}} C^{j}$
. By Lemma 5.8 in [Reference Braverman and Kappeler4], if
$C^{\operatorname {\mathrm {even}}}:=\bigoplus _{j \operatorname {\mathrm {even}}} C^{j}$
. By Lemma 5.8 in [Reference Braverman and Kappeler4], if
![]() $0 \notin I$
, then the complex
$0 \notin I$
, then the complex
![]() $(C^{*}_{I},\partial _{I})$
is acyclic. For every
$(C^{*}_{I},\partial _{I})$
is acyclic. For every
![]() $\lambda \geq 0$
, we have
$\lambda \geq 0$
, we have
In particular,
Hence, there are canonical isomorphisms
By [Reference Braverman and Kappeler4, Proposition 5.10], for each
![]() $\lambda \geq 0$
,
$\lambda \geq 0$
,
where
![]() $\rho _{\Gamma _{[0,\lambda ]}}$
is an element of
$\rho _{\Gamma _{[0,\lambda ]}}$
is an element of
![]() $\det (H^{*}(\partial ))$
via the canonical isomorphism
$\det (H^{*}(\partial ))$
via the canonical isomorphism
![]() $\Psi $
.
$\Psi $
.
11.2 Refined analytic torsion as an element of the determinant line for compact odd-dimensional manifolds
We consider now a compact, oriented, Riemannian manifold
![]() $(X,g)$
of odd dimension
$(X,g)$
of odd dimension
![]() $d=2r-1$
and a complex vector bundle E over X, endowed with a flat connection
$d=2r-1$
and a complex vector bundle E over X, endowed with a flat connection
![]() $\nabla $
. Let
$\nabla $
. Let
![]() $\Lambda ^{k}(X,E)$
be the space of k-differential forms on X with values in E. Let B be the odd signature operator acting on
$\Lambda ^{k}(X,E)$
be the space of k-differential forms on X with values in E. Let B be the odd signature operator acting on
![]() $\Lambda ^{k}(X,E)$
as in Definition 3.1.1. Let
$\Lambda ^{k}(X,E)$
as in Definition 3.1.1. Let
![]() $I\subset [0,\infty )$
. Let
$I\subset [0,\infty )$
. Let
![]() $\Lambda ^{k}_{I}(X,E)$
be the image of
$\Lambda ^{k}_{I}(X,E)$
be the image of
![]() $\Lambda ^{k}(X,E)$
under the spectral projection of
$\Lambda ^{k}(X,E)$
under the spectral projection of
![]() $B^{2}$
, corresponding to eigenvalues whose absolute value lie in I. If I is bounded, then the subspace
$B^{2}$
, corresponding to eigenvalues whose absolute value lie in I. If I is bounded, then the subspace
![]() $\Lambda ^{k}_{I}(X,E)$
is finite-dimensional ([Reference Braverman and Kappeler4, Section 6.10]). Let
$\Lambda ^{k}_{I}(X,E)$
is finite-dimensional ([Reference Braverman and Kappeler4, Section 6.10]). Let
![]() $B_{I}$
,
$B_{I}$
,
![]() $\Gamma _{I}$
be the restrictions to
$\Gamma _{I}$
be the restrictions to
![]() $\Lambda ^{k}_{I}(X,E)$
of B and
$\Lambda ^{k}_{I}(X,E)$
of B and
![]() $\Gamma $
, respectively. For every
$\Gamma $
, respectively. For every
![]() $\lambda \geq 0$
, we have
$\lambda \geq 0$
, we have
Since for every
![]() $\lambda \geq 0$
the complex
$\lambda \geq 0$
the complex
![]() $\Lambda ^{*}_{(\lambda ,\infty )}(X,E)$
is acyclic, we get
$\Lambda ^{*}_{(\lambda ,\infty )}(X,E)$
is acyclic, we get
Definition 11.2.1. The refined analytic torsion
![]() $T=T(\nabla )$
is an element of
$T=T(\nabla )$
is an element of
![]() $\det (H^{*}(X,E))$
, defined by
$\det (H^{*}(X,E))$
, defined by
where
![]() $\rho _{\Gamma _{[0,\lambda ]}}$
is as in Equation (11.2).
$\rho _{\Gamma _{[0,\lambda ]}}$
is as in Equation (11.2).
By [Reference Braverman and Kappeler4, Proposition 7.8] and [Reference Braverman and Kappeler4, Theorem 9.6], the refined analytic torsion is independent the choice of
![]() $\lambda \geq 0$
, the choice of the Agmon angle
$\lambda \geq 0$
, the choice of the Agmon angle
![]() $\theta \in (-\pi ,0)$
for
$\theta \in (-\pi ,0)$
for
![]() $B^{\operatorname {\mathrm {even}}}$
, and the Riemannian metric g.
$B^{\operatorname {\mathrm {even}}}$
, and the Riemannian metric g.
Acknowledgements
The author would like to thank Werner Müller for his helpful suggestions and comments, as well as Maxim Braverman for the insightful discussions. The author wishes to acknowledge also the hospitality of the Department of Mathematics of the University of Tübingen, Aarhus University and University of Göttingen. This work was partially funded by a research grant from the Villum Foundation (Grant No. 00025373) and the Research Training Group RTG 2491-Fourier Analysis and Spectral Theory.
Competing interest
None.