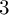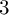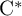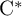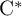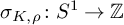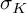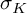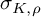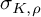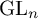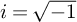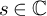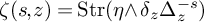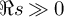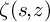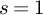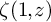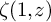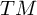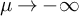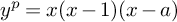Contents
Research Article
THE DIAGONAL CYCLE EULER SYSTEM FOR
 $\mathrm {GL}_2\times \mathrm {GL}_2$
$\mathrm {GL}_2\times \mathrm {GL}_2$
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1591-1653
-
- Article
- Export citation
Addendum
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS - ADDENDUM
-
- Published online by Cambridge University Press:
- 11 June 2025, p. 2133
-
- Article
- Export citation
Research Article
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
-
- Article
- Export citation
ALGEBRAIC CLASSES IN MIXED CHARACTERISTIC AND ANDRÉ’S p-ADIC PERIODS
-
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1093-1138
-
- Article
- Export citation
ON THE DEGREE OF IRRATIONALITY OF LOW GENUS
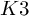 $K3$ SURFACES
$K3$ SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2025, pp. 627-662
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REDUCED QUIVER QUANTUM TOROIDAL ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 07 November 2024, pp. 341-369
-
- Article
- Export citation
STATED SKEIN MODULES OF 3-MANIFOLDS AND TQFT
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2025, pp. 663-703
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORAVA K-THEORY AND FILTRATIONS BY POWERS
- Part of:
-
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1655-1731
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
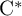 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED BLANCHFIELD PAIRINGS AND TWISTED SIGNATURES II: RELATION TO CASSON-GORDON INVARIANTS
-
- Published online by Cambridge University Press:
- 20 March 2025, pp. 1139-1195
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SIMPLE TRACIALLY
 $\mathcal {Z}$-ABSORBING C*-ALGEBRAS
$\mathcal {Z}$-ABSORBING C*-ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2025, pp. 2135-2179
-
- Article
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2024, pp. 17-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GAUSSIAN HOLOMORPHIC SECTIONS ON NONCOMPACT COMPLEX MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1197-1262
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
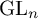 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2024, pp. 41-116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ODD RANK VECTOR BUNDLES IN ETA-PERIODIC MOTIVIC HOMOTOPY THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1733-1764
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGID INNER FORMS OVER GLOBAL FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2025, pp. 2181-2256
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOMBRE DE PETITS POINTS SUR UNE VARIÉTÉ ABÉLIENNE
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2025, pp. 705-761
-
- Article
- Export citation
ZETA INVARIANTS OF MORSE FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 10 October 2024, pp. 411-480
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARBITRARILY LARGE p-TORSION IN TATE-SHAFAREVICH GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 12 November 2024, pp. 481-502
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS
- Part of:
-
- Published online by Cambridge University Press:
- 25 November 2024, pp. 117-156
-
- Article
- Export citation

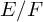

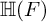
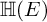
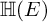
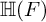
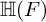
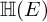
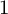

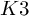
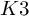
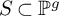
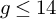
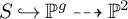 of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most
of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most 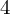
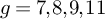
 of degree
of degree