Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T07:42:06.721Z Has data issue: false hasContentIssue false
  • English
  • Français

CUTOFF AT THE ENTROPIC TIME FOR RANDOM WALKS ON COVERED EXPANDER GRAPHS

Part of: Graph theory Markov processes

Published online by Cambridge University Press:  09 February 2021

Charles Bordenave  and
Hubert Lacoin Open the ORCID record for Hubert Lacoin [Opens in a new window]
Charles Bordenave
Affiliation:
Institut de Mathématiques de Marseille Université d'Aix-Marseille 163 avenue de Luminy - Case 907 13288 Marseille Cedex 9 - France (charles.bordenave@univ-amu.fr)
Hubert Lacoin
Affiliation:
IMPA Estrada Dona Castorina 110 Rio de Janeiro / Brasil22460-320 tel: +55 21 2529 5118 (lacoin@impa.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

It is a fact simple to establish that the mixing time of the simple random walk on a d-regular graph 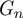$G_n$ with n vertices is asymptotically bounded from below by 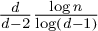$\frac {d }{d-2 } \frac {\log n}{\log (d-1)}$ . Such a bound is obtained by comparing the walk on 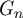$G_n$ to the walk on d-regular tree 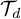$\mathcal{T}_d$ . If one can map another transitive graph 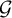$\mathcal{G} $ onto 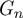$G_n$ , then we can improve the strategy by using a comparison with the random walk on 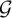$\mathcal{G} $ (instead of that of 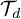$\mathcal{T} _d$ ), and we obtain a lower bound of the form 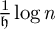$\frac {1}{\mathfrak{h} }\log n$ , where 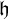$\mathfrak{h} $ is the entropy rate associated with 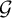$\mathcal{G} $ . We call this the entropic lower bound.

It was recently proved that in the case 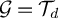$\mathcal{G} =\mathcal{T} _d$ , this entropic lower bound (in that case 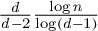$\frac {d }{d-2 } \frac {\log n}{\log (d-1)}$ ) is sharp when graphs have minimal spectral radius and thus that in that case the random walk exhibits cutoff at the entropic time. In this article, we provide a generalisation of the result by providing a sufficient condition on the spectra of the random walks on 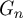$G_n$ under which the random walk exhibits cutoff at the entropic time. It applies notably to anisotropic random walks on random d-regular graphs and to random walks on random n-lifts of a base graph (including nonreversible walks).

Keywords

expander graphsmixing timespectral gapRamanujan graphentropic time

MSC classification

Primary: 05C81: Random walks on graphs 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 5 , September 2022 , pp. 1571 - 1616
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akemann, C. A. and Ostrand, P. A., Computing norms in group ${C}^{\ast }$ -algebras, Amer. J. Math. 98(4) (1976), 1015–1047.CrossRefGoogle Scholar
Aldous, D., Random walks on finite groups and rapidly mixing Markov chains, in Seminar on Probability, XVII, Vol. 986 of Lecture Notes in Mathematics, pp. 243–297 (Springer, Berlin, 1983).Google Scholar
Aldous, D. and Diaconis, P., Shuffling cards and stopping times, Amer. Math. Monthly 93 (1986), 333–348.CrossRefGoogle Scholar
Alon, N., Eigenvalues and expanders, Combinatorica 6(2) (1986), 83–96.CrossRefGoogle Scholar
Alon, N., Benjamini, I., Lubetzky, E. and Sodin, S., nonbacktracking random walks mix faster, Commun. Contemp. Math. 9(4) (2007), 585–603.Google Scholar
Amit, A. and Linial, N., Random graph coverings. I. General theory and graph connectivity, Combinatorica 22(1) (2002), 1–18.CrossRefGoogle Scholar
Amit, A. and Linial, N., Random lifts of graphs: edge expansion, Combin. Probab. Comput. 15(3) (2006), 317–332.Google Scholar
Avez, A., Entropie des groupes de type fini, C. R. Acad. Sci. Paris Sér. A-B 275 (1972), A1363–A1366.Google Scholar
Basu, R., Hermon, J. and Peres, Y., Characterization of cutoff for reversible Markov chains, Ann. Probab. 45(3) (2017), 1448–1487.CrossRefGoogle Scholar
Ben-Hamou, A. and Salez, J., Cutoff for nonbacktracking random walks on sparse random graphs, Ann. Probab. 45(3) (2017), 1752–1770.CrossRefGoogle Scholar
Berestycki, N., Lubetzky, E., Peres, Y. and Sly, A., Random walks on the random graph, Ann. Probab. 46(1) (2018), 456–490.CrossRefGoogle Scholar
Blachère, S., Haïssinsky, P. and Mathieu, P., Asymptotic entropy and Green speed for random walks on countable groups, Ann. Probab. 36(3) (2008), 1134–1152.CrossRefGoogle Scholar
Bordenave, C., A new proof of Friedman’s second eigenvalue theorem and its extension to random lifts. 2015, arXiv:1502.04482.Google Scholar
Bordenave, C., Caputo, P. and Salez, J., Random walk on sparse random digraphs, Probab. Theory Relat. Fields 170(3-4) (2018), 933–960.CrossRefGoogle Scholar
Bordenave, C. and Collins, B., Eigenvalues of random lifts and polynomials of random permutation matrices, Ann. Math. (2) 190(3) (2019), 811–875.Google Scholar
Cartier, P., Harmonic Analysis on Trees (American Mathematical Society, Providence, RI, 1973).CrossRefGoogle Scholar
Ceccherini-Silberstein, T., Scarabotti, F. and Tolli, F., Weighted expanders and the anisotropic Alon–Boppana theorem, Eur. J. Comb. 25(5) (2004), 735–744.CrossRefGoogle Scholar
Chatterji, I., Introduction to the rapid decay property, in Around Langlands Correspondences , Vol. 691 of Contemporary Mathematics (American Mathematical Society, Providence, RI, 2017).Google Scholar
Conchon-Kerjan, G., Cutoff for random lifts of weighted graphs, (2019), arXiv:1908.02898.Google Scholar
Diaconis, P., The cutoff phenomenon in finite Markov chains, Proc. Natl. Acad. Sci. U.S.A. 93(4) (1996), 1659–1664.CrossRefGoogle ScholarPubMed
Diaconis, P. and Shahshahani, M., Generating a random permutation with random transpositions, Probab. Theory Relat. Fields 57(2) (1981), 159–179.Google Scholar
Figà-Talamanca, A. and Steger, T., Harmonic analysis for anisotropic random walks on homogeneous trees, Mem. Amer. Math. Soc. 110(531) (1994), xii+68.Google Scholar
Friedman, J., Relative expanders or weakly relatively Ramanujan graphs, Duke Math. J. 118(1) (2003), 19–35.CrossRefGoogle Scholar
Gerl, P. and Woess, W., Local limits and harmonic functions for nonisotropic random walks on free groups, Probab. Theory Relat. Fields 71(3) (1986), 341–355.Google Scholar
Geronimus, J., On a set of polynomials, Ann. Math (2), 31(4) (1930), 681–686.CrossRefGoogle Scholar
Grigorchuk, R. I. and Żuk, A., On the asymptotic spectrum of random walks on infinite families of graphs, in Random Walks and Discrete Potential Theory (Cortona, 1997), pp. 188–204 (Cambridge University Press, Cambridge, 1999).Google Scholar
Haagerup, U., An example of a nonnuclear ${C}^{\ast }$ -algebra, which has the metric approximation property, Invent. Math. 50(3) (1978/79), 279–293.CrossRefGoogle Scholar
Haagerup, U. and Larsen, F., Brown’s spectral distribution measure for $R$ -diagonal elements in finite von Neumann algebras, J. Funct. Anal. 176(2) (2000), 331–367.CrossRefGoogle Scholar
Hermon, J., Cutoff for Ramanujan graphs via degree inflation, Electron. Commun. Probab. 22 (2017), 45.CrossRefGoogle Scholar
Hermon, J., A technical report on hitting times, mixing and cutoff, ALEA Lat. Am. J. Probab. Math. Stat. 15(1) (2018), 101–120.CrossRefGoogle Scholar
Ka anovich, V. A. and Vershik, A. M., Random walks on discrete groups: boundary and entropy, Ann. Probab. 11(3) (1983), 457–490.Google Scholar
Kesten, H., Full Banach mean values on countable groups, Math. Scand. 7 (1959), 146–156.CrossRefGoogle Scholar
Kesten, H., Symmetric random walks on groups, Trans. Amer. Math. Soc. 92 (1959), 336–354.CrossRefGoogle Scholar
Ledrappier, F., Some asymptotic properties of random walks on free groups, in Topics in Probability and Lie Groups: Boundary Theory, Vol. 28 of CRM Proceedings and Lecture Notes, pp. 117–152 (American Mathematical Society, Providence, RI, 2001).Google Scholar
Lehner, F., On the computation of spectra in free probability, J. Funct. Anal. 183(2) (2001), 451–471.CrossRefGoogle Scholar
Levin, D. A., Peres, Y. and Wilmer, E. L., Markov Chains and Mixing Times (American Mathematical Society, Providence, RI, 2017). Second edition of Markov Chains and Mixing Times (2017) Second Edition, With a chapter on “Coupling from the past” by James G. Propp and David B. Wilson.CrossRefGoogle Scholar
Lovász, L. and Plummer, M. D., Matching Theory (AMS Chelsea Publishing, Providence, RI, 2009).Google Scholar
Lubetzky, E. and Peres, Y., Cutoff on all Ramanujan graphs, Geom. Funct. Anal. 26(4) (2016), 1190–1216.Google Scholar
Lubetzky, E. and Sly, A., Cutoff phenomena for random walks on random regular graphs, Duke Math. J. 153(3) (2010), 475–510.CrossRefGoogle Scholar
Mingo, J. A. and Speicher, R., Free Probability and Random Matrices , Vol. 35 of Fields Institute Monographs (Springer, New York, 2017).Google Scholar
Mohar, B., A strengthening and a multipartite generalisation of the Alon-Boppana-Serre theorem, Proc. Amer. Math. Soc. 138(11) (2010), 3899–3909.CrossRefGoogle Scholar
Petersen, J., Die Theorie der regulären graphs, Acta Math. 15(1) (1891), 193–220.Google Scholar
Pisier, G., A simple proof of a theorem of Kirchberg and related results on ${C}^{\ast }$ -norms, J. Oper. Theory 35(2) (1996), 317–335.Google Scholar
Sodin, S., Random matrices, nonbacktracking walks, and orthogonal polynomials, J. Math. Phys. 48(12) (2007), 123503.CrossRefGoogle Scholar