1 Introduction
1.1 Motivation and main result
The anticanonical system is arguably the most natural object attached to a Fano manifold, and it plays an important role in the classification of Fano manifolds of low dimension. While it is expected that the anticanonical bundle always has global sections [10, Reference Ambro1, Reference Kawamata28], it is in general not globally generated. In dimension three, Shokurov’s theorem gives a complete description of the situation:
Theorem 1.1 [Reference Shokurov48].
Let X be a smooth Fano threefold such that the base locus
![]() $\mathrm {Bs}(|-K_X|)$
is not empty. Then the base locus is a smooth rational curve. Moreover, a general anticanonical divisor
$\mathrm {Bs}(|-K_X|)$
is not empty. Then the base locus is a smooth rational curve. Moreover, a general anticanonical divisor
![]() $Y \in |-K_X|$
is smooth.
$Y \in |-K_X|$
is smooth.
In dimension four, our current knowledge about the anticanonical system is very limited. An example by the first named author and Voisin shows that Shokurov’s theorem does not generalise to higher dimension:
Example 1.2 [Reference Höring and Voisin23, Example 2.12].
Let S be a smooth del Pezzo surface of degree one, and denote by
![]() $p \in S$
the unique base point of
$p \in S$
the unique base point of
![]() $|-K_S|$
. Set
$|-K_S|$
. Set
![]() $X:=S \times S$
, and let
$X:=S \times S$
, and let
![]() $Y \in |-K_X|$
be a general anticanonical divisor. Then Y is singular in the point
$Y \in |-K_X|$
be a general anticanonical divisor. Then Y is singular in the point
![]() $(p,p)$
.
$(p,p)$
.
Indeed, the threefold Y contains the base locus
![]() $\mathrm {Bs}(|-K_X|) = p \times S \cup S \times p$
which has embedding dimension four in the point
$\mathrm {Bs}(|-K_X|) = p \times S \cup S \times p$
which has embedding dimension four in the point
![]() $(p,p)$
. The varieties in Example 1.2 belong to the unique family of Fano fourfolds having the maximal Picard number 18 [Reference Casagrande9, Theorem 1.1], so one might hope that the presence of singular general anticanonical divisors is a rare pathology. In this paper, we destroy this hope by showing that a sufficiently large base locus always leads to singularities:
$(p,p)$
. The varieties in Example 1.2 belong to the unique family of Fano fourfolds having the maximal Picard number 18 [Reference Casagrande9, Theorem 1.1], so one might hope that the presence of singular general anticanonical divisors is a rare pathology. In this paper, we destroy this hope by showing that a sufficiently large base locus always leads to singularities:
Theorem 1.3. Let X be a smooth Fano fourfold such that
![]() $h^0(X, {\mathcal O}_X(-K_X)) \geq 3$
. Assume that the base locus
$h^0(X, {\mathcal O}_X(-K_X)) \geq 3$
. Assume that the base locus
![]() $\mathrm {Bs}(|-K_X|)$
is an irreducible normal surface. Then a general anticanonical divisor
$\mathrm {Bs}(|-K_X|)$
is an irreducible normal surface. Then a general anticanonical divisor
![]() $Y \in |-K_X|$
is not
$Y \in |-K_X|$
is not
![]() $\mathbb {Q}$
-factorial; in particular, it is singular.
$\mathbb {Q}$
-factorial; in particular, it is singular.
This theorem covers all the examples we know of smooth Fano fourfolds such that
![]() $\mathrm {Bs}(|-K_X|)$
is an irreducible surface; cf. Examples 3.2, 3.3, 3.4. These examples differ from Example 1.2 in a significant way: they have moving singularities (i.e., the singular locus
$\mathrm {Bs}(|-K_X|)$
is an irreducible surface; cf. Examples 3.2, 3.3, 3.4. These examples differ from Example 1.2 in a significant way: they have moving singularities (i.e., the singular locus
![]() $Y_{\operatorname *{\mathrm {sing}}} \subset \mathrm {Bs}(|-K_X|)$
depends on the choice of
$Y_{\operatorname *{\mathrm {sing}}} \subset \mathrm {Bs}(|-K_X|)$
depends on the choice of
![]() $Y \in |-K_X|$
). Theorem 1.3 is almost optimal: if the base scheme
$Y \in |-K_X|$
). Theorem 1.3 is almost optimal: if the base scheme
![]() $\mathbf {Bs}(|-K_X|)$
is smooth of dimension at most one, a general anticanonical divisor Y is smooth by a strong version of Bertini’s theorem [Reference Diaz and Harbater12, Corollary 2.4]. It seems likely that Theorem 1.3 still holds under the relaxed assumption that
$\mathbf {Bs}(|-K_X|)$
is smooth of dimension at most one, a general anticanonical divisor Y is smooth by a strong version of Bertini’s theorem [Reference Diaz and Harbater12, Corollary 2.4]. It seems likely that Theorem 1.3 still holds under the relaxed assumption that
![]() $\mathrm {Bs}(|-K_X|)$
contains a surface. However, this additional generality leads to numerous case distinctions in our proofs, a technicality that we wanted to avoid.
$\mathrm {Bs}(|-K_X|)$
contains a surface. However, this additional generality leads to numerous case distinctions in our proofs, a technicality that we wanted to avoid.
While our main result states that the anticanonical geometry of a Fano fourfold is more complicated than in dimension three, the tools developed in this paper indicate that two-dimensional base loci lead to numerous restrictions on the geometry and the numerical invariants. Therefore, Theorem 1.3 is actually a first step towards the classification of Fano fourfolds with large anticanonical base locus. We plan to come back to this topic in the near future.
1.2 The setup
Let X be a smooth Fano fourfold such that
![]() $h^0(X, {\mathcal O}_X(-K_X)) \geq 3$
and
$h^0(X, {\mathcal O}_X(-K_X)) \geq 3$
and
![]() $\mathrm {Bs}(|-K_X|)$
is an irreducible normal surface B.
$\mathrm {Bs}(|-K_X|)$
is an irreducible normal surface B.
Let
![]() $Y \in |-K_X|$
be a general anticanonical divisor, so Y is a normal threefold (Corollary 2.8). By Kodaira, vanishing the restriction morphism
$Y \in |-K_X|$
be a general anticanonical divisor, so Y is a normal threefold (Corollary 2.8). By Kodaira, vanishing the restriction morphism
is surjective. Thus, we know that
and
![]() $h^0(Y, {\mathcal O}_Y(-K_X))=h^0(X, {\mathcal O}_X(-K_X))-1 \geq 2$
. Denote by
$h^0(Y, {\mathcal O}_Y(-K_X))=h^0(X, {\mathcal O}_X(-K_X))-1 \geq 2$
. Denote by
![]() $|M|$
the mobile part of the linear system
$|M|$
the mobile part of the linear system
![]() $|-K_X|_Y|$
. Then we have a linear equivalence of effective Weil divisors
$|-K_X|_Y|$
. Then we have a linear equivalence of effective Weil divisors
The proof of Theorem 1.3 will be by contradiction, so we make the following assumption.
Assumption 1.4. We assume that Y is
![]() $\mathbb {Q}$
-factorial.
$\mathbb {Q}$
-factorial.
Combined with the known results about anticanonical divisors (cf. Corollary 2.9), this assumption implies that the Weil divisors M and B are Cartier. By Grothendieck’s Lefschetz hyperplane theorem [Reference Lazarsfeld39, Example 3.1.25], the restriction morphism
is an isomorphism, so there exists uniquely defined Cartier divisor classes
![]() $M_X \rightarrow X$
and
$M_X \rightarrow X$
and
![]() $B_X \rightarrow X$
such that
$B_X \rightarrow X$
such that
Note that it is not clear whether the divisors
![]() $M_X$
and
$M_X$
and
![]() $B_X$
are effective, establishing this will be an important first step in our proof.
$B_X$
are effective, establishing this will be an important first step in our proof.
1.3 General strategy and structure of the proof
The proof of Shokurov’s theorem 1.1 can be split into two steps, cf. [Reference Iskovskikh and Prokhorov24, \S 2.3]: first, one shows that Y has canonical singularities. Then one applies Mayer’s theorem to a minimal resolution
![]() $Y' \rightarrow Y$
.
$Y' \rightarrow Y$
.
Theorem 1.5 [Reference Mayer42, Proposition 5].
Let S be a smooth K3 surface, and let A be a nef and big Cartier divisor on S such that
![]() $\mathrm {Bs}(|A|) \neq \emptyset $
. Then we have a decomposition into fixed and mobile part
$\mathrm {Bs}(|A|) \neq \emptyset $
. Then we have a decomposition into fixed and mobile part
where
![]() $B \simeq \mathbb {P}^1$
and M is a nef divisor that defines an elliptic fibration
$B \simeq \mathbb {P}^1$
and M is a nef divisor that defines an elliptic fibration
![]() $\varphi _{|M|}: S \rightarrow \mathbb {P}^1$
.
$\varphi _{|M|}: S \rightarrow \mathbb {P}^1$
.
Since the first part of Shokurov’s proof also works for Fano fourfolds [Reference Kawamata28, Theorem 5.2], the most natural approach would be to look for an analogue of Mayer’s theorem for Calabi-Yau threefolds (with mild singularities). This approach immediately encounters two obstacles: while it is easy to classify fixed prime divisors on a K3 surface (they are
![]() $(-2)$
-curves), there are many possibilities on a Calabi-Yau threefold (e.g., Enriques surfaces [Reference Borisov and Nuer7, Theorem 3.1]). Moreover, the mobile part of a linear system on a surface is always nef. This is not true on a threefold.
$(-2)$
-curves), there are many possibilities on a Calabi-Yau threefold (e.g., Enriques surfaces [Reference Borisov and Nuer7, Theorem 3.1]). Moreover, the mobile part of a linear system on a surface is always nef. This is not true on a threefold.
The second obstacle leads to a basic case distinction in our proof: if
![]() $M_X$
is nef, the basepoint free theorem yields a morphism
$M_X$
is nef, the basepoint free theorem yields a morphism
![]() $X \rightarrow T$
that we can use to study the anticanonical system. This situation is close to the Examples 3.2, 3.3, 3.4, and we will need a series of rather specific classification results to settle this case in Section 7.
$X \rightarrow T$
that we can use to study the anticanonical system. This situation is close to the Examples 3.2, 3.3, 3.4, and we will need a series of rather specific classification results to settle this case in Section 7.
In the second case,
![]() $M_X$
is not nef. We use the embedding
$M_X$
is not nef. We use the embedding
![]() $Y \subset X$
in a more direct way. We start by showing that
$Y \subset X$
in a more direct way. We start by showing that
![]() $-K_X+M_X$
is nef and big (i.e., the anticanonical divisor compensates the negativity of
$-K_X+M_X$
is nef and big (i.e., the anticanonical divisor compensates the negativity of
![]() $M_X$
). This allows us to show that the surface B is a complete intersection: we find an effective divisor
$M_X$
). This allows us to show that the surface B is a complete intersection: we find an effective divisor
![]() $B_X$
with canonical singularities such that
$B_X$
with canonical singularities such that
Moreover, using an extension theorem of Fujino, we obtain that the restriction map
is surjective. Combined with some classification results for linear systems on irregular surfaces (cf. Section 4), we exclude this possibility.
1.4 Future research
In Theorem 1.3, we make the assumption that
![]() $h^0(X, {\mathcal O}_X(-K_X)) \geq 3$
, an assumption that is satisfied by all smooth Fano fourfolds that we are aware of.Footnote
1
Riemann-Roch computations only show that
$h^0(X, {\mathcal O}_X(-K_X)) \geq 3$
, an assumption that is satisfied by all smooth Fano fourfolds that we are aware of.Footnote
1
Riemann-Roch computations only show that
![]() $h^0(X, {\mathcal O}_X(-K_X)) \geq 2$
(Theorem 2.8), so it would be highly desirable to have an answer to the following
$h^0(X, {\mathcal O}_X(-K_X)) \geq 2$
(Theorem 2.8), so it would be highly desirable to have an answer to the following
Problem 1.6 [Reference Fujita15, Reference Küchle37, Reference Liu41].
Is there a smooth Fano fourfold X with
![]() $h^0(X, {\mathcal O}_X(-K_X)) = 2$
?
$h^0(X, {\mathcal O}_X(-K_X)) = 2$
?
Is there a smooth Calabi-Yau threefold Y with an ample Cartier divisor A such that
![]() $h^0(Y, {\mathcal O}_Y(A))=1$
?
$h^0(Y, {\mathcal O}_Y(A))=1$
?
Beauville [Reference Beauville6] gave an example of a numerical Calabi-Yau threefold with a fixed ample divisor. For our purpose, we are interested in strict Calabi-Yau’s (i.e., Y is simply connected).
A significant problem in this theory is the lack of interesting examples. Our Example 3.4 generalises a construction from the threefold case, but it is still related to the del Pezzo surface of degree one.
Problem 1.7. Construct new examples of smooth Fano fourfolds X such that
![]() ${\mathrm {Bs}(|-K_X|)}$
has dimension two.
${\mathrm {Bs}(|-K_X|)}$
has dimension two.
2 Notation and basic facts
We work over
![]() $\mathbb {C}$
; for general definitions, we refer to [Reference Hartshorne20]. All the schemes appearing in this paper are projective; manifolds and normal varieties will always be supposed to be irreducible. For notions of positivity of divisors and vector bundles, we refer to Lazarsfeld’s book [Reference Lazarsfeld39, Reference Lazarsfeld40]. Given two Cartier divisors
$\mathbb {C}$
; for general definitions, we refer to [Reference Hartshorne20]. All the schemes appearing in this paper are projective; manifolds and normal varieties will always be supposed to be irreducible. For notions of positivity of divisors and vector bundles, we refer to Lazarsfeld’s book [Reference Lazarsfeld39, Reference Lazarsfeld40]. Given two Cartier divisors
![]() $D_1, D_2$
on a projective variety, we denote by
$D_1, D_2$
on a projective variety, we denote by
![]() $D_1 \simeq D_2$
(resp.
$D_1 \simeq D_2$
(resp.
![]() $D_1 \equiv D_2$
) the linear equivalence (resp. numerical equivalence) of the Cartier divisor classes. Given a Cartier divisor D, we will denote by
$D_1 \equiv D_2$
) the linear equivalence (resp. numerical equivalence) of the Cartier divisor classes. Given a Cartier divisor D, we will denote by
![]() ${\mathcal O}_X(D)$
both the associated invertible sheaf and the corresponding line bundle. Somewhat abusively we will say that a Cartier divisor class is effective if it contains an effective divisor.
${\mathcal O}_X(D)$
both the associated invertible sheaf and the corresponding line bundle. Somewhat abusively we will say that a Cartier divisor class is effective if it contains an effective divisor.
We use the terminology of [Reference Kollár and Mori31] for birational geometry and of [Reference Kollár34] for rational curves. We refer to [Reference Kollár35] for the definitions and basic facts about singularities of the MMP.
Given a normal projective surface S with Gorenstein singularities, we will denote by
the irregularity, and by
the geometric genus.
Definition 2.1. Let Y be a projective variety, and let D be a nef Cartier divisor on Y. The numerical dimension
![]() $\nu (Y,D)$
is defined as
$\nu (Y,D)$
is defined as
We collect a number of basic facts for the convenience of the reader:
Fact 2.2. Let A be a Cartier divisor on a projective variety Y such that the complete linear system
![]() $|A|$
has a non-empty fixed part B. Then
$|A|$
has a non-empty fixed part B. Then
![]() $h^0(Y,{\mathcal O}_Y(B))=1$
.
$h^0(Y,{\mathcal O}_Y(B))=1$
.
Fact 2.3. Let X be a Fano manifold, and let D be a nef Cartier divisor on X. Then there exists a morphism with connected fibres
![]() $\varphi :X \rightarrow T$
and an ample Cartier divisor
$\varphi :X \rightarrow T$
and an ample Cartier divisor
![]() $H_T$
on T such that
$H_T$
on T such that
![]() $D \simeq \varphi ^* H_T$
.
$D \simeq \varphi ^* H_T$
.
Proof. By the basepoint free theorem, we have
![]() $mD \simeq \varphi ^* H_m$
for some very ample divisor
$mD \simeq \varphi ^* H_m$
for some very ample divisor
![]() $H_m \rightarrow T$
for every
$H_m \rightarrow T$
for every
![]() $m \gg 0$
. Thus,
$m \gg 0$
. Thus,
![]() $H_T := H_{m+1}-H_m$
is a Cartier divisor such that
$H_T := H_{m+1}-H_m$
is a Cartier divisor such that
![]() $D \simeq \varphi ^* H_T$
. Since D is numerically the pull-back of an ample class on T, the divisor
$D \simeq \varphi ^* H_T$
. Since D is numerically the pull-back of an ample class on T, the divisor
![]() $H_T$
is ample.
$H_T$
is ample.
Fact 2.4. Let S be an irreducible projective surface with Gorenstein singularities, and let
![]() $C \subset S$
be an irreducible curve that is not contained in the singular locus of S. If
$C \subset S$
be an irreducible curve that is not contained in the singular locus of S. If
![]() $-K_S \cdot C \geq 2$
, the curve C deforms in S in a positive-dimensional family.
$-K_S \cdot C \geq 2$
, the curve C deforms in S in a positive-dimensional family.
Proof. Let
![]() $\tau :S' \rightarrow S$
be the composition of normalisation and minimal resolution. Then we have
$\tau :S' \rightarrow S$
be the composition of normalisation and minimal resolution. Then we have
![]() $K_{S'} \simeq \tau ^* K_S - E$
, where E is an effective divisor that maps into the singular locus of S. Thus, if
$K_{S'} \simeq \tau ^* K_S - E$
, where E is an effective divisor that maps into the singular locus of S. Thus, if
![]() $C' \subset S'$
is the strict transform, it is not contained in the support of E. Thus, we have
$C' \subset S'$
is the strict transform, it is not contained in the support of E. Thus, we have
The statement now follows from [Reference Kollár34, Theorem 1.15].
Fact 2.5 [Reference Beltrametti and Sommese8, Lemma 2.4.1].
Let X be a normal projective variety with rational singularities such that
![]() $q(X)>0$
. Then the Albanese map
$q(X)>0$
. Then the Albanese map
![]() $\alpha :X \rightarrow A$
to the Albanese torus exists and is determined by the Albanese map of some resolution of singularities.
$\alpha :X \rightarrow A$
to the Albanese torus exists and is determined by the Albanese map of some resolution of singularities.
Fact 2.6. Let S be a normal projective surface with rational singularities, and let A be a Cartier divisor on S. Then the Riemann-Roch formula
holds.
Let Y be a normal projective threefold with terminal singularities, and let A be a Cartier divisor on Y. Then the Riemann-Roch formula
holds.
Proof. It is sufficient to verify that all the terms are well-defined and can be calculated on a resolution of singularities. This is well-known; cf. [Reference Höring22, Section 2]. The statement then follows via the projection formula.
In the rest of the paper, we will refer to the following set of statements by inversion of adjunction:
Theorem 2.7 [Reference Kollár and Mori31, Theorem 5.50] [Reference Kawakita29, Theorem] [Reference Kollár35, Theorem 4.9].
Let X be a normal projective variety, and let
![]() $S \subset X$
be a reduced Weil divisor that is Cartier in codimension two. Let
$S \subset X$
be a reduced Weil divisor that is Cartier in codimension two. Let
![]() $\Delta $
be an effective boundary divisor on X that has no common component with S such that
$\Delta $
be an effective boundary divisor on X that has no common component with S such that
![]() $K_X+S+\Delta $
is
$K_X+S+\Delta $
is
![]() $\mathbb {Q}$
-Cartier. Then the following holds:
$\mathbb {Q}$
-Cartier. Then the following holds:
-
• The pair
 $(X, S+\Delta )$
is lc near S if and only if the pair
$(X, S+\Delta )$
is lc near S if and only if the pair
 $(S, \Delta |_S)$
is slc.
$(S, \Delta |_S)$
is slc. -
• The pair
 $(X, S+\Delta )$
is plt near S if and only if the pair
$(X, S+\Delta )$
is plt near S if and only if the pair
 $(S, \Delta |_S)$
is klt.
$(S, \Delta |_S)$
is klt.
2.1 Anticanonical divisors on Fano fourfolds
The following statement collects the known results about anticanonical divisors on smooth Fano fourfolds
Theorem 2.8 [Reference Kawamata28, Theorem 5.2],[Reference Höring and Voisin23, Theorem 1.7], [Reference Heuberger21, Theorem 2].
Let X be a smooth Fano fourfold. Then we have
Let
![]() $Y \in |-K_X|$
be a general anticanonical divisor. Then Y is a normal prime divisor with terminal Gorenstein singularities. The variety Y is Calabi-Yau, that is,
$Y \in |-K_X|$
be a general anticanonical divisor. Then Y is a normal prime divisor with terminal Gorenstein singularities. The variety Y is Calabi-Yau, that is,
![]() $K_Y \simeq {\mathcal O}_Y$
and
$K_Y \simeq {\mathcal O}_Y$
and
In fact, the possible singularities of Y are completely described by [Reference Heuberger21, Theorem 4], but we will not need this description for our proof. By [Reference Kawamata25, Lemma 5.1], a terminal
![]() $\mathbb {Q}$
-factorial Gorenstein threefold singularity is factorial, so Theorem 2.8 implies the following:
$\mathbb {Q}$
-factorial Gorenstein threefold singularity is factorial, so Theorem 2.8 implies the following:
Corollary 2.9. Let X be a smooth Fano fourfold. If a general anticanonical divisor Y is
![]() $\mathbb {Q}$
-factorial, it is factorial.
$\mathbb {Q}$
-factorial, it is factorial.
Theorem 2.10 [Reference Kollár33, Theorem].
Let X be a Fano manifold of dimension at least four, and let
![]() $Y \in |-K_X|$
be an irreducibleFootnote
2
anticanonical divisor. Then the inclusion
$Y \in |-K_X|$
be an irreducibleFootnote
2
anticanonical divisor. Then the inclusion
is a bijection. Equivalently, a Cartier divisor
![]() $D \rightarrow X$
is nef if and only if its restriction
$D \rightarrow X$
is nef if and only if its restriction
![]() $D|_Y$
is nef.
$D|_Y$
is nef.
Theorem 2.11 [Reference Kawamata28, Proposition 4.2].
Let Y be a normal projective threefold with canonical Gorenstein singularities such that
![]() $c_1(Y)=0$
. Let
$c_1(Y)=0$
. Let
![]() $A \rightarrow Y$
be an ample Cartier divisor, and let
$A \rightarrow Y$
be an ample Cartier divisor, and let
![]() $D \in |A|$
be a general element. Then the pair
$D \in |A|$
be a general element. Then the pair
![]() $(Y, D)$
is lc.
$(Y, D)$
is lc.
Corollary 2.12. In the situation of Setup 1.2, let M be a general element of the mobile part of
![]() $|-K_X|_Y|$
. Then the pair
$|-K_X|_Y|$
. Then the pair
![]() $(Y, M+B)$
is lc, and hence, the pairs
$(Y, M+B)$
is lc, and hence, the pairs
![]() $(Y, M)$
and
$(Y, M)$
and
![]() $(Y,B)$
are lc. In particular, B is a normal projective Gorenstein surface with at most lc singularities and
$(Y,B)$
are lc. In particular, B is a normal projective Gorenstein surface with at most lc singularities and
![]() $p_g(B)=0$
. Moreover,
$p_g(B)=0$
. Moreover,
is an lc pair such that
is ample with
![]() $(K_B+M|_B) \cdot M|_B>0$
.
$(K_B+M|_B) \cdot M|_B>0$
.
Proof. Since M is a general divisor in the mobile part, the divisor
![]() $M+B$
is general in
$M+B$
is general in
![]() $|-K_X|_Y|$
. Thus,
$|-K_X|_Y|$
. Thus,
![]() $(Y, M+B)$
is lc by Theorem 2.11. The statement for
$(Y, M+B)$
is lc by Theorem 2.11. The statement for
![]() $(Y, M)$
and
$(Y, M)$
and
![]() $(Y,B)$
is now immediate since we assume that Y is
$(Y,B)$
is now immediate since we assume that Y is
![]() $\mathbb {Q}$
-factorial. By adjunction (Theorem 2.7), this implies that the surfaces M and B have at most slc singularities. Since B is normal by assumption, it has lc singularities. Consider the cohomology sequence associated to the exact sequence
$\mathbb {Q}$
-factorial. By adjunction (Theorem 2.7), this implies that the surfaces M and B have at most slc singularities. Since B is normal by assumption, it has lc singularities. Consider the cohomology sequence associated to the exact sequence
The Calabi-Yau threefold Y has
![]() $h^1(Y, {\mathcal O}_Y)=0$
and
$h^1(Y, {\mathcal O}_Y)=0$
and
![]() $h^0(Y, {\mathcal O}_Y(B))=1$
by Fact 2.2, so
$h^0(Y, {\mathcal O}_Y(B))=1$
by Fact 2.2, so
![]() $p_g(B)=h^0(B, {\mathcal O}_B(K_B))=0$
.
$p_g(B)=h^0(B, {\mathcal O}_B(K_B))=0$
.
Again, by adjunction, the pair
![]() $(B, M|_B)$
is slc (hence lc) since
$(B, M|_B)$
is slc (hence lc) since
![]() $(Y, M+B)$
is lc. Since
$(Y, M+B)$
is lc. Since
![]() $K_Y$
is trivial, the linear equivalence (1) follows from the adjunction formula. Finally, observe that the support of the divisor
$K_Y$
is trivial, the linear equivalence (1) follows from the adjunction formula. Finally, observe that the support of the divisor
![]() $M+B \simeq -K_X|_Y$
is connected since it is ample. Therefore, the intersection
$M+B \simeq -K_X|_Y$
is connected since it is ample. Therefore, the intersection
![]() $M \cap B$
has positive dimension and
$M \cap B$
has positive dimension and
![]() $(K_B+M|_B) \cdot M|_B = -K_X|_B \cdot M|_B>0$
.
$(K_B+M|_B) \cdot M|_B = -K_X|_B \cdot M|_B>0$
.
3 Examples and first observations
We start this section by collecting some arguments that give a moral explanation for Theorem 1.3.
Lemma 3.1. Let X be a projective manifold, and let A be an ample divisor on X. Let
![]() $B \subset \mathrm {Bs}(|A|)$
be a submanifold of dimension at least
$B \subset \mathrm {Bs}(|A|)$
be a submanifold of dimension at least
![]() $\frac {\dim X}{2}$
such that the conormal bundle
$\frac {\dim X}{2}$
such that the conormal bundle
![]() ${\mathcal N}_{B/X}^*$
is nef. Then every divisor
${\mathcal N}_{B/X}^*$
is nef. Then every divisor
![]() $Y \in |A|$
has at least one singular point along B.
$Y \in |A|$
has at least one singular point along B.
Proof. Consider the natural morphism
By [Reference Beltrametti and Sommese8, Lemma 1.7.4], the divisor Y is smooth along B if and only if the section
![]() $\alpha (s) \in H^0(B, {\mathcal I}_B/{\mathcal I}_B^2 \otimes {\mathcal O}_X(A))$
is nowhere zero, where
$\alpha (s) \in H^0(B, {\mathcal I}_B/{\mathcal I}_B^2 \otimes {\mathcal O}_X(A))$
is nowhere zero, where
![]() $0 \neq s \in H^0(X, {\mathcal O}_X(A))$
is a section vanishing on Y. Since
$0 \neq s \in H^0(X, {\mathcal O}_X(A))$
is a section vanishing on Y. Since
![]() ${\mathcal I}_B/{\mathcal I}_B^2 \otimes {\mathcal O}_X(A) \simeq {\mathcal N}_{B/X}^* \otimes {\mathcal O}_X(A)$
is a tensor product of a nef vector bundle and an ample line bundle, it is ample [Reference Lazarsfeld40, Theorem 6.2.12.(iv)]. Set
${\mathcal I}_B/{\mathcal I}_B^2 \otimes {\mathcal O}_X(A) \simeq {\mathcal N}_{B/X}^* \otimes {\mathcal O}_X(A)$
is a tensor product of a nef vector bundle and an ample line bundle, it is ample [Reference Lazarsfeld40, Theorem 6.2.12.(iv)]. Set
![]() $d=\mathrm {codim}_X B$
. If
$d=\mathrm {codim}_X B$
. If
![]() $\alpha (s)$
does not vanish in any point of B, the top Chern class
$\alpha (s)$
does not vanish in any point of B, the top Chern class
![]() $c_d({\mathcal N}_{B/X}^* \otimes {\mathcal O}_X(A))$
is zero. Yet since
$c_d({\mathcal N}_{B/X}^* \otimes {\mathcal O}_X(A))$
is zero. Yet since
![]() $d \leq \dim B$
, this is a contradiction to the positivity of Chern classes of ample vector bundles [Reference Lazarsfeld40, Theorem 8.3.9].
$d \leq \dim B$
, this is a contradiction to the positivity of Chern classes of ample vector bundles [Reference Lazarsfeld40, Theorem 8.3.9].
Remark. The key point of the proof above is that the vector bundle
![]() ${\mathcal N}_{B/X}^* \otimes {\mathcal O}_X(A)$
is ample, and one may wonder if this holds without any assumption on
${\mathcal N}_{B/X}^* \otimes {\mathcal O}_X(A)$
is ample, and one may wonder if this holds without any assumption on
![]() ${\mathcal N}_{B/X}^*$
: as a toy case, assume that the base scheme
${\mathcal N}_{B/X}^*$
: as a toy case, assume that the base scheme
![]() $\mathbf {Bs}(|A|)$
is the submanifold B. We can resolve the indeterminacies of
$\mathbf {Bs}(|A|)$
is the submanifold B. We can resolve the indeterminacies of
![]() $\varphi _{|A|}$
by blowing up B and compute that
$\varphi _{|A|}$
by blowing up B and compute that
![]() ${\mathcal N}_{B/X}^* \otimes {\mathcal O}_X(A)$
is nef. However, it is not clear if the vector bundle is ample; in fact, this is impossible if
${\mathcal N}_{B/X}^* \otimes {\mathcal O}_X(A)$
is nef. However, it is not clear if the vector bundle is ample; in fact, this is impossible if
![]() $h^0(X, {\mathcal O}_X(A)) \leq \dim X-1$
.
$h^0(X, {\mathcal O}_X(A)) \leq \dim X-1$
.
The lemma allows to cover all the known examples of Fano fourfolds with a two-dimensional base locus:
Example 3.2. Let
![]() $X = S_1 \times S$
be the product of smooth del Pezzo surface
$X = S_1 \times S$
be the product of smooth del Pezzo surface
![]() $S_1$
of degree one and S a smooth del Pezzo surface of degree at least two. Then every anticanonical divisor
$S_1$
of degree one and S a smooth del Pezzo surface of degree at least two. Then every anticanonical divisor
![]() $Y \in |-K_X|$
is singular.
$Y \in |-K_X|$
is singular.
Proof. The base locus is
![]() $B=p \times S$
, where
$B=p \times S$
, where
![]() $p =\text {Bs}(|-K_{S_1}|)$
. Thus,
$p =\text {Bs}(|-K_{S_1}|)$
. Thus,
![]() ${\mathcal N}^*_{B/X} \simeq {\mathcal O}_B^{\oplus 2}$
is trivial, and Lemma 3.1 applies.
${\mathcal N}^*_{B/X} \simeq {\mathcal O}_B^{\oplus 2}$
is trivial, and Lemma 3.1 applies.
Applied to an irreducible component of the base locus, the argument above also works for [Reference Höring and Voisin23, Example 2.12].
Example 3.3. Let
![]() $X = Z \times \mathbb {P}^1$
, where Z is a smooth Fano threefold such that
$X = Z \times \mathbb {P}^1$
, where Z is a smooth Fano threefold such that
![]() $C :=\mathrm {Bs}(|-K_{Z}|)$
is not empty. Then every anticanonical divisor
$C :=\mathrm {Bs}(|-K_{Z}|)$
is not empty. Then every anticanonical divisor
![]() $Y \in |-K_X|$
is singular.
$Y \in |-K_X|$
is singular.
Proof. The base locus is
![]() $B=C \times \mathbb {P}^1$
, and we know that
$B=C \times \mathbb {P}^1$
, and we know that
![]() ${\mathcal N}^*_{C/Z} \simeq {\mathcal O}_C^{\oplus 2}$
or
${\mathcal N}^*_{C/Z} \simeq {\mathcal O}_C^{\oplus 2}$
or
![]() ${\mathcal N}^*_{C/Z} \simeq {\mathcal O}_C \oplus {\mathcal O}_C(1)$
(cf. the proof of [Reference Iskovskikh and Prokhorov24, Lemma 2.4.4]). Thus,
${\mathcal N}^*_{C/Z} \simeq {\mathcal O}_C \oplus {\mathcal O}_C(1)$
(cf. the proof of [Reference Iskovskikh and Prokhorov24, Lemma 2.4.4]). Thus,
![]() ${\mathcal N}^*_{B/X}$
is nef, and Lemma 3.1 applies.
${\mathcal N}^*_{B/X}$
is nef, and Lemma 3.1 applies.
The next manifold is a generalisation of a well-known example in the threefold case [Reference Mori and Mukai44, Table 2, No 1].
Example 3.4. For
![]() $n \geq 4$
, let M be a general sextic hypersurface in the weighted projective space
$n \geq 4$
, let M be a general sextic hypersurface in the weighted projective space
![]() $\mathbb {P}(1^n, 2, 3)$
. Then M is a del Pezzo manifold of dimension n and degree
$\mathbb {P}(1^n, 2, 3)$
. Then M is a del Pezzo manifold of dimension n and degree
![]() $1$
[Reference Fujita16, Theorem 8.11] (i.e., we have
$1$
[Reference Fujita16, Theorem 8.11] (i.e., we have
![]() $-K_M \simeq (n-1) A$
with A an ample Cartier divisor such that
$-K_M \simeq (n-1) A$
with A an ample Cartier divisor such that
![]() $A^n=1$
). The del Pezzo manifold M has a ladder [Reference Fujita16, Theorem 3.5]; that is, we can choose
$A^n=1$
). The del Pezzo manifold M has a ladder [Reference Fujita16, Theorem 3.5]; that is, we can choose
![]() $n-1$
general elements
$n-1$
general elements
![]() $D_1, \ldots , D_{n-1}$
in the linear system
$D_1, \ldots , D_{n-1}$
in the linear system
![]() $|A|$
such that
$|A|$
such that
is a smooth elliptic curve. Morever,
![]() $|A|$
has a unique base-point p.
$|A|$
has a unique base-point p.
Let now
![]() $\mu :X \rightarrow M$
be the blow-up along C, and denote by E the exceptional divisor. Then
$\mu :X \rightarrow M$
be the blow-up along C, and denote by E the exceptional divisor. Then
![]() $\mu $
resolves the base locus of the linear system
$\mu $
resolves the base locus of the linear system
![]() $|V|$
generated by
$|V|$
generated by
![]() $D_1, \ldots , D_{n-1}$
, so we have a fibration
$D_1, \ldots , D_{n-1}$
, so we have a fibration
such that
![]() $\mu ^* A \simeq f^* H + E$
, where H is the hyperplane divisor on
$\mu ^* A \simeq f^* H + E$
, where H is the hyperplane divisor on
![]() $\mathbb {P}^{n-2}$
. Using the Nakai-Moishezon criterion, we obtain immediately that
$\mathbb {P}^{n-2}$
. Using the Nakai-Moishezon criterion, we obtain immediately that
is ample, so X is a Fano manifold. The general f-fibre is a surface S obtained as the complete intersection of
![]() $n-2$
elements in
$n-2$
elements in
![]() $|V|$
, so it is a del Pezzo surface of degree one. In particular,
$|V|$
, so it is a del Pezzo surface of degree one. In particular,
![]() $|-K_S|$
has a unique base point
$|-K_S|$
has a unique base point
![]() $p_S$
such that
$p_S$
such that
![]() $\mu (p_S)=p$
. This implies that
$\mu (p_S)=p$
. This implies that
![]() $\mu ^{-1} (p) \simeq \mathbb {P}^{n-2}$
is contained in
$\mu ^{-1} (p) \simeq \mathbb {P}^{n-2}$
is contained in
![]() $\mathrm {Bs}(|-K_X|)$
.
$\mathrm {Bs}(|-K_X|)$
.
Since
![]() ${\mathcal N}^*_{\mathbb {P}^{n-2}/X} \simeq {\mathcal O}_{\mathbb {P}^{n-2}} \oplus {\mathcal O}_{\mathbb {P}^{n-2}} (1)$
is nef, we can apply Lemma 3.1 to see that all the anticanonical divisors in X are singular.
${\mathcal N}^*_{\mathbb {P}^{n-2}/X} \simeq {\mathcal O}_{\mathbb {P}^{n-2}} \oplus {\mathcal O}_{\mathbb {P}^{n-2}} (1)$
is nef, we can apply Lemma 3.1 to see that all the anticanonical divisors in X are singular.
Remark 3.5. Let X be a complex manifold, and let
![]() $B \subset X$
be a submanifold of codimension two. Let
$B \subset X$
be a submanifold of codimension two. Let
![]() $B \subset Y \subset X$
be a normal prime divisor. Then Y is singular in a point
$B \subset Y \subset X$
be a normal prime divisor. Then Y is singular in a point
![]() $p \in B$
if and only if Y is not factorial in p. Indeed, if Y is factorial in p, the Weil divisor
$p \in B$
if and only if Y is not factorial in p. Indeed, if Y is factorial in p, the Weil divisor
![]() $B \subset Y$
is Cartier near the point p. Thus, if Y is singular in p, so is the Cartier divisor B.
$B \subset Y$
is Cartier near the point p. Thus, if Y is singular in p, so is the Cartier divisor B.
The next statement shows that for most prime Fano manifolds (i.e., the prime Fanos with index one), the presence of a codimension two base locus is incompatible with the smoothness of the anticanonical divisor.
Proposition 3.6. Let X be a Fano manifold of dimension at least four with Picard number one such that
![]() $h^0(X, {\mathcal O}_X(-K_X)) \geq 3$
. Assume that the base locus
$h^0(X, {\mathcal O}_X(-K_X)) \geq 3$
. Assume that the base locus
![]() $\mathrm {Bs}(|-K_X|)$
has codimension two and a general anticanonical divisor
$\mathrm {Bs}(|-K_X|)$
has codimension two and a general anticanonical divisor
![]() $Y \in |-K_X|$
is smooth. Then X has Fano index at least three.
$Y \in |-K_X|$
is smooth. Then X has Fano index at least three.
Proof. Let
be the decomposition into fixed and mobile part. Since Y is smooth, the Weil divisors M and B are Cartier. Since
![]() $\dim X \geq 4$
and
$\dim X \geq 4$
and
![]() $\rho (X)=1$
, the Lefschetz hyperplane theorem implies
$\rho (X)=1$
, the Lefschetz hyperplane theorem implies
![]() $\operatorname *{\mathrm {Pic}}{Y} \simeq \operatorname *{\mathrm {Pic}}{X} \simeq \mathbb {Z} H$
, where H is the ample generator of the Picard group. Thus, we have
$\operatorname *{\mathrm {Pic}}{Y} \simeq \operatorname *{\mathrm {Pic}}{X} \simeq \mathbb {Z} H$
, where H is the ample generator of the Picard group. Thus, we have
with
![]() $a,b \in \mathbb {N}^*$
. Since
$a,b \in \mathbb {N}^*$
. Since
![]() $h^0(Y, {\mathcal O}_Y(B))=1$
and
$h^0(Y, {\mathcal O}_Y(B))=1$
and
![]() $h^0(Y, {\mathcal O}_Y(M)) \geq 2$
, we have
$h^0(Y, {\mathcal O}_Y(M)) \geq 2$
, we have
![]() $a>b$
, and therefore,
$a>b$
, and therefore,
![]() $a+b \geq 3$
. Since
$a+b \geq 3$
. Since
the statement follows from
![]() $\operatorname *{\mathrm {Pic}}{Y} \simeq \operatorname *{\mathrm {Pic}}{X}$
.
$\operatorname *{\mathrm {Pic}}{Y} \simeq \operatorname *{\mathrm {Pic}}{X}$
.
Lemma 3.7. Let X be a smooth Fano fourfold, and let D be a non-zero nef Cartier divisor on X. Then
![]() $h^0(X, {\mathcal O}_X(D)) \geq 2$
.
$h^0(X, {\mathcal O}_X(D)) \geq 2$
.
Proof. If D has numerical dimension one, there exists a fibration
![]() $\varphi : X \rightarrow \mathbb {P}^1$
such that
$\varphi : X \rightarrow \mathbb {P}^1$
such that
![]() $D \simeq \varphi ^* H$
with H an ample Cartier divisor on
$D \simeq \varphi ^* H$
with H an ample Cartier divisor on
![]() $\mathbb {P}^1$
(cf. Fact 2.3). Thus,
$\mathbb {P}^1$
(cf. Fact 2.3). Thus,
![]() $h^0(\mathbb {P}^1, {\mathcal O}_{\mathbb {P}^1}(H)) \geq 2$
yields the claim.
$h^0(\mathbb {P}^1, {\mathcal O}_{\mathbb {P}^1}(H)) \geq 2$
yields the claim.
If D has numerical dimension at least two, we have
![]() $D^2 \cdot K_X^2= D^2 \cdot (-K_X)^2>0$
. Moreover,
$D^2 \cdot K_X^2= D^2 \cdot (-K_X)^2>0$
. Moreover,
![]() $h^0(X, {\mathcal O}_X(D))=\chi (X, {\mathcal O}_X(D))$
by Kodaira vanishing, and by Riemann-Roch,
$h^0(X, {\mathcal O}_X(D))=\chi (X, {\mathcal O}_X(D))$
by Kodaira vanishing, and by Riemann-Roch,
 $$ \begin{align*} \chi(X, {\mathcal O}_X(D)) &= \frac{D^4}{4!} - \frac{D^3 \cdot K_X}{2 \cdot 3!} + \frac{D^2 \cdot (K_X^2+c_2(X))}{12 \cdot 2 !} - \frac{D \cdot K_X \cdot c_2(X)}{24 \cdot 1!} + \chi(X, {\mathcal O}_X) \\ & \geq \frac{D^2 \cdot (-K_X)^2}{24} + \frac{D^2 \cdot c_2(X)}{24} - \frac{D \cdot K_X \cdot c_2(X)}{24} + 1. \end{align*} $$
$$ \begin{align*} \chi(X, {\mathcal O}_X(D)) &= \frac{D^4}{4!} - \frac{D^3 \cdot K_X}{2 \cdot 3!} + \frac{D^2 \cdot (K_X^2+c_2(X))}{12 \cdot 2 !} - \frac{D \cdot K_X \cdot c_2(X)}{24 \cdot 1!} + \chi(X, {\mathcal O}_X) \\ & \geq \frac{D^2 \cdot (-K_X)^2}{24} + \frac{D^2 \cdot c_2(X)}{24} - \frac{D \cdot K_X \cdot c_2(X)}{24} + 1. \end{align*} $$
Since
![]() $-K_X \cdot D \cdot c_2(X) \geq 0$
and
$-K_X \cdot D \cdot c_2(X) \geq 0$
and
![]() $D^2 \cdot c_2(X) \geq 0$
by [Reference Peternell46, Theorem 1.3], [Reference Miyaoka43, Theorem 6.1] we obtain that the second line is at least two.
$D^2 \cdot c_2(X) \geq 0$
by [Reference Peternell46, Theorem 1.3], [Reference Miyaoka43, Theorem 6.1] we obtain that the second line is at least two.
Lemma 3.8. Let X be a smooth Fano fourfold, and let L be a line bundle on X such that
![]() $h^0(X, L) \neq 0$
. Let
$h^0(X, L) \neq 0$
. Let
![]() $D \in |L|$
be a general divisor, and assume that for a general anticanonical divisor
$D \in |L|$
be a general divisor, and assume that for a general anticanonical divisor
![]() $Y \in |-K_X|$
, the pair
$Y \in |-K_X|$
, the pair
![]() $(Y, D \cap Y)$
is log-canonical. Then the pair
$(Y, D \cap Y)$
is log-canonical. Then the pair
![]() $(X,D)$
is log-canonical.
$(X,D)$
is log-canonical.
Proof. Since
![]() $\dim X \leq 4$
, the anticanonical system
$\dim X \leq 4$
, the anticanonical system
![]() $|-K_X|$
has no fixed component; cf. Theorem 2.8. In particular, Y has no common component with D.
$|-K_X|$
has no fixed component; cf. Theorem 2.8. In particular, Y has no common component with D.
We argue by contradiction and assume that the non-lc locus Z is not empty.
1st step. Assume that Z has positive dimension. Since Y is an ample divisor, it intersects Z in at least one point, so the pair
![]() $(X,D)$
is not lc near Y. Thus, the pair
$(X,D)$
is not lc near Y. Thus, the pair
![]() $(X, D+Y)$
is not lc near Y. By Theorem 2.7, this is a contradiction to Corollary 2.12.
$(X, D+Y)$
is not lc near Y. By Theorem 2.7, this is a contradiction to Corollary 2.12.
2nd step. Assume that Z has dimension zero. We endow
![]() $Z \subset X$
with its natural scheme structure; cf. [Reference Fujino17, \S 7]. Since
$Z \subset X$
with its natural scheme structure; cf. [Reference Fujino17, \S 7]. Since
is ample, we can apply Fujino’s extension theorem (with W the empty set; cf. [Reference Fujino17, Theorem 8.1]) to see that the restriction map
is surjective. Since Z is a finite scheme, the restriction
![]() $L|_Z$
is globally generated. Thus, L is globally generated near Z; in particular, a general
$L|_Z$
is globally generated. Thus, L is globally generated near Z; in particular, a general
![]() $D \in |L|$
is smooth near Z. Hence, the pair
$D \in |L|$
is smooth near Z. Hence, the pair
![]() $(X,D)$
is lc, a contradiction.
$(X,D)$
is lc, a contradiction.
4 Auxiliary results about linear systems, part I
In Section 5, our study of the Fano fourfold X will lead to several restrictions on the geometry of the base locus
![]() $\mathrm {Bs}(|-K_X|)$
. These restrictions can be strengthened when combined with the technical results of this section.
$\mathrm {Bs}(|-K_X|)$
. These restrictions can be strengthened when combined with the technical results of this section.
Lemma 4.1. Let S be a normal projective surface with canonical singularities such that
![]() $p_g(S)=0$
. Assume that the Albanese map induces a fibration
$p_g(S)=0$
. Assume that the Albanese map induces a fibration
![]() $\alpha :S \rightarrow C$
onto a curve of genus
$\alpha :S \rightarrow C$
onto a curve of genus
![]() $g=q(S)>0$
. Then the general
$g=q(S)>0$
. Then the general
![]() $\alpha $
-fibre is
$\alpha $
-fibre is
![]() $\mathbb {P}^1$
or
$\mathbb {P}^1$
or
![]() $g=1$
.
$g=1$
.
Proof. Since canonical surface singularities are rational, we can replace S with a resolution of singularities. Thus, S is a smooth surface with
![]() $p_g(S)=0$
and
$p_g(S)=0$
and
![]() $q(S) \geq 1$
. If the general
$q(S) \geq 1$
. If the general
![]() $\alpha $
-fibre is not
$\alpha $
-fibre is not
![]() $\mathbb {P}^1$
, the surface S is not uniruled. Thus, we can apply [Reference Beauville5, Theorem VI.13] to the minimal model of S to obtain that
$\mathbb {P}^1$
, the surface S is not uniruled. Thus, we can apply [Reference Beauville5, Theorem VI.13] to the minimal model of S to obtain that
![]() $q(S)=1$
.
$q(S)=1$
.
Proposition 4.2. Let S be a normal projective Gorenstein surface with
![]() $p_g(S)=0$
, and let A be a nef and big Cartier divisor on S such that
$p_g(S)=0$
, and let A be a nef and big Cartier divisor on S such that
where
![]() $\Delta _S$
is an effective Weil divisor such that the pair
$\Delta _S$
is an effective Weil divisor such that the pair
![]() $(S, \Delta _S)$
is lc and
$(S, \Delta _S)$
is lc and
![]() $A \cdot \Delta _S>0$
. Assume that we have
$A \cdot \Delta _S>0$
. Assume that we have
Then S has canonical singularities, and the Albanese map induces a fibration
onto a curve of genus
![]() $q(S)>0$
. Set
$q(S)>0$
. Set
![]() $r:=\mathrm {rk} (\alpha _* {\mathcal O}_S(A))$
. Then we have
$r:=\mathrm {rk} (\alpha _* {\mathcal O}_S(A))$
. Then we have
Moreover, we have
Remark. In the second step of the proof, we will use the following fact that follows easily from the Leray spectral sequence: let S be a normal projective surface with Gorenstein singularities such that
![]() $p_g(S)=0$
. Assume that S has irrational (hence non-canonical [Reference Kollár and Mori31, Corollary 5.24]) singularities, and let
$p_g(S)=0$
. Assume that S has irrational (hence non-canonical [Reference Kollár and Mori31, Corollary 5.24]) singularities, and let
![]() $\tau :S_c \rightarrow S$
be the canonical modification [Reference Kollár35, Theorem 1.31]. Then we have
$\tau :S_c \rightarrow S$
be the canonical modification [Reference Kollár35, Theorem 1.31]. Then we have
Proof of Proposition 4.2.
Since
![]() $A \cdot \Delta _S>0$
, we have
$A \cdot \Delta _S>0$
, we have
![]() $\Delta _S \neq 0$
. Thus,
$\Delta _S \neq 0$
. Thus,
and we have the inequalities
1st step. Assume that S has canonical singularities. By Fact 2.6, we have the Riemann-Roch formula
Hence,
![]() $A \cdot \Delta _S>0$
implies that
$A \cdot \Delta _S>0$
implies that
![]() $q(S)> \chi (S, {\mathcal O}_S) = 1 - q(S)$
. In particular, we have
$q(S)> \chi (S, {\mathcal O}_S) = 1 - q(S)$
. In particular, we have
![]() $q(S)>0$
, so there is a non-trivial Albanese morphism
$q(S)>0$
, so there is a non-trivial Albanese morphism
![]() $\alpha $
. If
$\alpha $
. If
![]() $\dim \alpha (S)=2$
, the ramification formula shows that
$\dim \alpha (S)=2$
, the ramification formula shows that
![]() $p_g(S)>0$
which we excluded. Thus, the Albanese morphism gives a fibration [Reference Beltrametti and Sommese8, Lemma 2.4.5]
$p_g(S)>0$
which we excluded. Thus, the Albanese morphism gives a fibration [Reference Beltrametti and Sommese8, Lemma 2.4.5]
onto a curve C of genus
![]() $g:=q(S)>0$
. Since the pair
$g:=q(S)>0$
. Since the pair
![]() $(S, \Delta _S)$
is lc, the direct image sheaf
$(S, \Delta _S)$
is lc, the direct image sheaf
is a nef vector bundle [Reference Fujino19, Theorem 1.1] of rank r. Thus,
has
![]() $c_1(V) \geq r (2g-2)$
. By the Riemann-Roch formula on curves, we have
$c_1(V) \geq r (2g-2)$
. By the Riemann-Roch formula on curves, we have
Now observe that
![]() $r(g-1)> g$
unless
$r(g-1)> g$
unless
![]() $(r-1) (g-1) \leq 1$
.
$(r-1) (g-1) \leq 1$
.
Finally, let us show that we have
![]() $h^0(S, {\mathcal O}_S(A)) = q(S)$
: if
$h^0(S, {\mathcal O}_S(A)) = q(S)$
: if
![]() $h^0(S, {\mathcal O}_S(A)) \leq q(S)-1$
, the Riemann-Roch estimate (2) becomes
$h^0(S, {\mathcal O}_S(A)) \leq q(S)-1$
, the Riemann-Roch estimate (2) becomes
![]() $g-1 \geq r (g-1)$
.
$g-1 \geq r (g-1)$
.
Subcase a) Assume that
![]() $g>1$
. Then the unique possibility
$g>1$
. Then the unique possibility
![]() $r=1$
. Since A is nef and big, this implies that the general
$r=1$
. Since A is nef and big, this implies that the general
![]() $\alpha $
-fibre is not
$\alpha $
-fibre is not
![]() $\mathbb {P}^1$
. Yet this contradicts Lemma 4.1.
$\mathbb {P}^1$
. Yet this contradicts Lemma 4.1.
Subcase b) Assume that
![]() $g=1$
. In this case, the Riemann-Roch inequality becomes
$g=1$
. In this case, the Riemann-Roch inequality becomes
so
![]() $h^0(S, {\mathcal O}_S(K_S+\Delta _S)) \geq 1 = g$
.
$h^0(S, {\mathcal O}_S(K_S+\Delta _S)) \geq 1 = g$
.
2nd step. We show that S has canonical singularities. Since S is Gorenstein, it has canonical singularities if and only if it has rational singularities. Arguing by contradiction, we assume that S has non-canonical singularities and denote by
![]() $\tau :S_c \rightarrow S$
the canonical modification. Then we have
$\tau :S_c \rightarrow S$
the canonical modification. Then we have
![]() $K_{S_c} \simeq \tau ^* K_S - E$
with E an effective Weil divisor. Observe that
$K_{S_c} \simeq \tau ^* K_S - E$
with E an effective Weil divisor. Observe that
so the pair
![]() $(S_c, \Delta _{S_c}) := (S_c, E + \tau ^* \Delta _S)$
is lc. Moreover,
$(S_c, \Delta _{S_c}) := (S_c, E + \tau ^* \Delta _S)$
is lc. Moreover,
is a nef and big Cartier divisor with
![]() $A_c \cdot \Delta _{S_c}=A \cdot \Delta _S>0$
and
$A_c \cdot \Delta _{S_c}=A \cdot \Delta _S>0$
and
![]() $h^0(S, {\mathcal O}_S(A)) = h^0(S_c, {\mathcal O}_{S_c}(A_c))$
. Finally, by the remark before the proof, one has
$h^0(S, {\mathcal O}_S(A)) = h^0(S_c, {\mathcal O}_{S_c}(A_c))$
. Finally, by the remark before the proof, one has
![]() $p_g(S_c) \leq p_g(S)=0$
and
$p_g(S_c) \leq p_g(S)=0$
and
![]() $q(S_c)>q(S)$
. Therefore, by Step 1 of the proof,
$q(S_c)>q(S)$
. Therefore, by Step 1 of the proof,
a contradiction to our assumption.
The conditions in Proposition 4.2 are very restrictive; however, there is a classical example that will play a prominent role in Section 7:
Example 4.3. Let C be an elliptic curve, and for some point
![]() $p \in C$
, let
$p \in C$
, let
be an unsplit extension. Set
![]() $\alpha :S:=\mathbb {P}(V) \rightarrow C$
and denote by
$\alpha :S:=\mathbb {P}(V) \rightarrow C$
and denote by
![]() $\zeta _S$
the tautological class on S. Set
$\zeta _S$
the tautological class on S. Set
![]() $\Delta _S := 3 \zeta _S - \alpha ^* p$
. Then
$\Delta _S := 3 \zeta _S - \alpha ^* p$
. Then
![]() $\Delta _S$
is an ample divisor [Reference Hartshorne20, V, Proposition 2.21] such that
$\Delta _S$
is an ample divisor [Reference Hartshorne20, V, Proposition 2.21] such that
![]() $|\Delta _S|$
contains an element with normal crossing singularities. Thus, the pair
$|\Delta _S|$
contains an element with normal crossing singularities. Thus, the pair
![]() $(S, \Delta _S)$
is lc, and
$(S, \Delta _S)$
is lc, and
is an ample divisor with
![]() $h^0(S, {\mathcal O}_S(A))=1=q(S)$
.
$h^0(S, {\mathcal O}_S(A))=1=q(S)$
.
Since it would be tedious to go into the classification of surfaces with small invariants, we want a convenient criterion to exclude this kind of exceptional surfaces in the proof of Theorem 1.3:
Proposition 4.4. Let S be a normal projective Gorenstein surface with
![]() $p_g(S)=0$
, and let A be an ample Cartier divisor on S such that
$p_g(S)=0$
, and let A be an ample Cartier divisor on S such that
where
![]() $\Delta _S$
is an effective Weil divisor such that the pair
$\Delta _S$
is an effective Weil divisor such that the pair
![]() $(S, \Delta _S)$
is lc. Assume that we have
$(S, \Delta _S)$
is lc. Assume that we have
Then
![]() $\Delta _S$
does not contain any smooth rational curve.
$\Delta _S$
does not contain any smooth rational curve.
Proof. We argue by contradiction, so let
![]() $l \subset \Delta _S$
be a smooth rational curve. In particular,
$l \subset \Delta _S$
be a smooth rational curve. In particular,
![]() $\Delta _S \neq 0$
, and therefore,
$\Delta _S \neq 0$
, and therefore,
![]() $A\cdot \Delta _S>0$
. By Proposition 4.2, the surface has canonical singularities, and we have an Albanese fibration
$A\cdot \Delta _S>0$
. By Proposition 4.2, the surface has canonical singularities, and we have an Albanese fibration
![]() $\alpha :S \rightarrow C$
onto a smooth curve C of genus
$\alpha :S \rightarrow C$
onto a smooth curve C of genus
![]() $g=q(S)$
. Moreover, we have
$g=q(S)$
. Moreover, we have
where
![]() $r= \mathrm {rk} (\alpha _* {\mathcal O}_S(A))$
.
$r= \mathrm {rk} (\alpha _* {\mathcal O}_S(A))$
.
1st case. Assume that
![]() $g>1$
. By Lemma 4.1, the general
$g>1$
. By Lemma 4.1, the general
![]() $\alpha $
-fibre F is
$\alpha $
-fibre F is
![]() $\mathbb {P}^1$
. Since
$\mathbb {P}^1$
. Since
![]() $A \cdot F \geq 1$
, we have
$A \cdot F \geq 1$
, we have
![]() $r \geq 2$
, and thus, (3) yields
$r \geq 2$
, and thus, (3) yields
![]() $g=2$
and
$g=2$
and
![]() $r=2$
. Moreover,
$r=2$
. Moreover,
![]() $A \cdot F=1$
implies that
$A \cdot F=1$
implies that
![]() $\alpha :S \rightarrow C$
is a
$\alpha :S \rightarrow C$
is a
![]() $\mathbb {P}^1$
-bundle over the genus two curve C [Reference Kollár34, II,Theorem 2.8]. In particular, the rational curve l is a fibre of
$\mathbb {P}^1$
-bundle over the genus two curve C [Reference Kollár34, II,Theorem 2.8]. In particular, the rational curve l is a fibre of
![]() $\alpha $
, and thus a nef divisor on S. The pair
$\alpha $
, and thus a nef divisor on S. The pair
![]() $(S, \Delta _S-l)$
is lc, so the direct image
$(S, \Delta _S-l)$
is lc, so the direct image
is a nef vector bundle [Reference Fujino19, Theorem 1.1]. Thus,
![]() $\alpha _* {\mathcal O}_S(A)$
has degree at least six. By the Riemann-Roch formula on the curve C, this implies
$\alpha _* {\mathcal O}_S(A)$
has degree at least six. By the Riemann-Roch formula on the curve C, this implies
![]() $h^0(S, {\mathcal O}_S(A))=h^0(C, \alpha _* {\mathcal O}_S(A)) \geq 4$
, a contradiction.
$h^0(S, {\mathcal O}_S(A))=h^0(C, \alpha _* {\mathcal O}_S(A)) \geq 4$
, a contradiction.
2nd case. Assume that
![]() $g=1$
. By Proposition 4.2, we have
$g=1$
. By Proposition 4.2, we have
![]() $h^0(S, {\mathcal O}_S(A))=1$
, and thus by Riemann-Roch,
$h^0(S, {\mathcal O}_S(A))=1$
, and thus by Riemann-Roch,
Therefore,
![]() $A \cdot \Delta _S = (K_S+\Delta _S) \cdot \Delta _S=2$
, and Lemma 4.5 applies: all the irreducible components of
$A \cdot \Delta _S = (K_S+\Delta _S) \cdot \Delta _S=2$
, and Lemma 4.5 applies: all the irreducible components of
![]() $\Delta _S$
are rational curves, so they are contracted by the Albanese map. Moreover, the support of
$\Delta _S$
are rational curves, so they are contracted by the Albanese map. Moreover, the support of
![]() $\Delta _S$
is connected, so it is contained in an
$\Delta _S$
is connected, so it is contained in an
![]() $\alpha $
-fibre
$\alpha $
-fibre
![]() $F_0$
. Since
$F_0$
. Since
![]() $p_a(\Delta _S)=2$
, we deduce that
$p_a(\Delta _S)=2$
, we deduce that
![]() $p_a(F_0) \geq 2$
. Since the arithmetic genus is constant in the flat family
$p_a(F_0) \geq 2$
. Since the arithmetic genus is constant in the flat family
![]() $\alpha :S \rightarrow C$
, we obtain that S is not uniruled. Let
$\alpha :S \rightarrow C$
, we obtain that S is not uniruled. Let
![]() $\tau :S' \rightarrow S$
be the minimal resolution, and let
$\tau :S' \rightarrow S$
be the minimal resolution, and let
![]() $\nu :S' \rightarrow S_m$
the minimal model of
$\nu :S' \rightarrow S_m$
the minimal model of
![]() $S'$
. Since S has canonical singularities, we have
$S'$
. Since S has canonical singularities, we have
By [Reference Beauville5, Proposition VI.6], the minimal surface
![]() $S_m$
does not contain any rational curves. Since the exceptional divisors of the resolution
$S_m$
does not contain any rational curves. Since the exceptional divisors of the resolution
![]() $\tau $
are rational curves, the rigidity lemma [Reference Debarre11, Lemma 1.15] yields a birational map
$\tau $
are rational curves, the rigidity lemma [Reference Debarre11, Lemma 1.15] yields a birational map
![]() $\nu :S \rightarrow S_m$
that contracts all the rational curves on S. In particular, it contracts the divisor
$\nu :S \rightarrow S_m$
that contracts all the rational curves on S. In particular, it contracts the divisor
![]() $\Delta _S$
. Yet
$\Delta _S$
. Yet
![]() $p_a(\Delta _S)=2>0$
, a contradiction to the fact that the smooth surface
$p_a(\Delta _S)=2>0$
, a contradiction to the fact that the smooth surface
![]() $S_m$
has rational singularities.
$S_m$
has rational singularities.
Lemma 4.5. Let S be a normal projective surface with canonical singularities and
![]() $p_g(S)=0$
, and let A be an ample Cartier divisor on S such that
$p_g(S)=0$
, and let A be an ample Cartier divisor on S such that
where
![]() $\Delta _S$
is an effective Weil divisor such that the pair
$\Delta _S$
is an effective Weil divisor such that the pair
![]() $(S, \Delta _S)$
is lc and
$(S, \Delta _S)$
is lc and
![]() $A \cdot \Delta _S=2$
. Assume that
$A \cdot \Delta _S=2$
. Assume that
![]() $\Delta _S$
has an irreducible component that is a smooth rational curve l. Then the support of
$\Delta _S$
has an irreducible component that is a smooth rational curve l. Then the support of
![]() $\Delta _S$
is connected, and all its irreducible components are rational curves.
$\Delta _S$
is connected, and all its irreducible components are rational curves.
Proof. Recall first that canonical surface singularities are Gorenstein, so both
![]() $K_S$
and
$K_S$
and
![]() $\Delta _S = A-K_S$
are Cartier. We have
$\Delta _S = A-K_S$
are Cartier. We have
![]() $p_a(\Delta _S)=2$
, so the inclusion
$p_a(\Delta _S)=2$
, so the inclusion
![]() $l \subset \Delta _S$
must be strict. Since A is ample with
$l \subset \Delta _S$
must be strict. Since A is ample with
![]() $A \cdot \Delta _S=2$
, we obtain
$A \cdot \Delta _S=2$
, we obtain
with R an irreducible curve such that
![]() $A \cdot R=1$
. In particular, we have by subadjunction
$A \cdot R=1$
. In particular, we have by subadjunction
so
![]() $p_a(R)=\frac {1}{2} \deg K_R + 1 \leq 1$
. In particular,
$p_a(R)=\frac {1}{2} \deg K_R + 1 \leq 1$
. In particular,
![]() $\Delta _S$
is connected because otherwise
$\Delta _S$
is connected because otherwise
yields a contradiction.
Let
![]() $\tau :S' \rightarrow S$
be the minimal resolution and set
$\tau :S' \rightarrow S$
be the minimal resolution and set
Since
![]() $\Delta _S$
is connected, the cycle
$\Delta _S$
is connected, the cycle
![]() $\Delta _{S'}$
is connected. Denote by
$\Delta _{S'}$
is connected. Denote by
![]() $R' \subset \Delta _{S'}$
the strict transform of R. We claim that
$R' \subset \Delta _{S'}$
the strict transform of R. We claim that
![]() $R'$
is a rational curve, and this concludes the proof.
$R'$
is a rational curve, and this concludes the proof.
Proof of the claim. Since S has canonical singularities, the minimal resolution
![]() $\tau $
is crepant, so we have
$\tau $
is crepant, so we have
![]() $K_{S'} \simeq \tau ^* K_S$
and
$K_{S'} \simeq \tau ^* K_S$
and
Thus, we have
If we show that
![]() $(\Delta _{S'}-R') \cdot R'\geq 2$
, then the adjunction formula yields the claim. Since
$(\Delta _{S'}-R') \cdot R'\geq 2$
, then the adjunction formula yields the claim. Since
![]() $\Delta _{S'}$
is connected, we have
$\Delta _{S'}$
is connected, we have
![]() $(\Delta _{S'}-R') \cdot R'\geq 1$
. We will argue by contradiction to exclude the case where we have an equality.
$(\Delta _{S'}-R') \cdot R'\geq 1$
. We will argue by contradiction to exclude the case where we have an equality.
In this case,
![]() $R'$
is a curve of arithmetic genus one that meets
$R'$
is a curve of arithmetic genus one that meets
![]() $\Delta _{S'}-R'$
transversally exactly in one point. In particular, we have
$\Delta _{S'}-R'$
transversally exactly in one point. In particular, we have
The curve
![]() $l \subset S$
being smooth, it meets the exceptional divisor over every point
$l \subset S$
being smooth, it meets the exceptional divisor over every point
![]() $p \in l \cap S_{sing}$
in exactly one point, and the intersection is transverse. Thus, we have
$p \in l \cap S_{sing}$
in exactly one point, and the intersection is transverse. Thus, we have
since the exceptional divisors of the minimal resolution of an ADE-singularity have arithmetic genus zero. This gives the final contradiction.
5 Positivity arguments
This section is the technical core of the paper. We will study the positivity properties of the Cartier classes
![]() $M_X$
and
$M_X$
and
![]() $B_X$
and successively improve our knowledge about the existence and singularities of effective divisors contained in these classes.
$B_X$
and successively improve our knowledge about the existence and singularities of effective divisors contained in these classes.
Proposition 5.1. In the situation of Setup 1.2, the divisor
![]() $B_X$
is not nef. If
$B_X$
is not nef. If
![]() $B_X$
is effective, then
$B_X$
is effective, then
![]() $h^0(X, {\mathcal O}_X(B_X))=1$
and
$h^0(X, {\mathcal O}_X(B_X))=1$
and
![]() $B_X$
is a normal prime divisor.
$B_X$
is a normal prime divisor.
Proof. Consider the exact sequence
We have
![]() $h^0(X, {\mathcal O}_X(-M_X))=0$
since otherwise
$h^0(X, {\mathcal O}_X(-M_X))=0$
since otherwise
![]() $-M_X$
, and thus its restriction
$-M_X$
, and thus its restriction
![]() $-M$
to the general anticanonical divisor Y, is effective. Thus, we have an injection
$-M$
to the general anticanonical divisor Y, is effective. Thus, we have an injection
Since
![]() $h^0(Y, {\mathcal O}_Y(B))=1$
by Fact 2.2, we have
$h^0(Y, {\mathcal O}_Y(B))=1$
by Fact 2.2, we have
![]() $h^0(X, {\mathcal O}_X(B_X)) \leq 1$
. By Lemma 3.7, this implies that
$h^0(X, {\mathcal O}_X(B_X)) \leq 1$
. By Lemma 3.7, this implies that
![]() $B_X$
is not nef.
$B_X$
is not nef.
If
![]() $B_X$
is effective, it is a normal prime divisor since its restriction to the ample divisor Y is the normal prime divisor B.
$B_X$
is effective, it is a normal prime divisor since its restriction to the ample divisor Y is the normal prime divisor B.
Proposition 5.2. Let Y be a
![]() $\mathbb {Q}$
-factorial threefold with canonical Gorenstein singularities such that
$\mathbb {Q}$
-factorial threefold with canonical Gorenstein singularities such that
![]() $c_1(Y)=0$
. Let A be an ample Cartier divisor with
$c_1(Y)=0$
. Let A be an ample Cartier divisor with
![]() $h^0(Y, {\mathcal O}_Y(A)) \geq 2$
such that
$h^0(Y, {\mathcal O}_Y(A)) \geq 2$
such that
![]() $\mathrm {Bs}( |A|)$
has pure dimension two. Let
$\mathrm {Bs}( |A|)$
has pure dimension two. Let
![]() $A \simeq M+B$
be the decomposition into mobile part and fixed part B. Then
$A \simeq M+B$
be the decomposition into mobile part and fixed part B. Then
![]() $A+M$
is a nef and big divisor.
$A+M$
is a nef and big divisor.
Proof. We choose a general element M in the mobile part, so by Theorem 2.11, the pair
![]() $(Y, M+B)$
is lc. If
$(Y, M+B)$
is lc. If
![]() $A+M$
is not nef, there exists an irreducible curve
$A+M$
is not nef, there exists an irreducible curve
![]() $\gamma $
such that
$\gamma $
such that
![]() $(A+M) \cdot \gamma <0$
. Since A is ample, we have
$(A+M) \cdot \gamma <0$
. Since A is ample, we have
![]() $M \cdot \gamma \leq -2$
. In particular, we have
$M \cdot \gamma \leq -2$
. In particular, we have
![]() $\gamma \subset \mathrm {Bs}(|M|)$
. Since
$\gamma \subset \mathrm {Bs}(|M|)$
. Since
![]() $|M|$
is the mobile part of
$|M|$
is the mobile part of
![]() $|A|$
, we have
$|A|$
, we have
![]() $\mathrm {Bs}(|M|) \subset \mathrm {Bs}(|A|)$
. By assumption,
$\mathrm {Bs}(|M|) \subset \mathrm {Bs}(|A|)$
. By assumption,
![]() $\mathrm {Bs}(|A|)$
has pure dimension two, so it coincides with B. Thus, we have
$\mathrm {Bs}(|A|)$
has pure dimension two, so it coincides with B. Thus, we have
![]() $\gamma \subset B,$
and hence,
$\gamma \subset B,$
and hence,
The surface
![]() $M+B$
is slc by Theorem 2.7, so it has normal crossing singularities in codimension one. Therefore, B and M are smooth in the generic point of
$M+B$
is slc by Theorem 2.7, so it has normal crossing singularities in codimension one. Therefore, B and M are smooth in the generic point of
![]() $\gamma $
; in particular,
$\gamma $
; in particular,
![]() $\gamma $
is not contained in the singular locus of M. Since
$\gamma $
is not contained in the singular locus of M. Since
we know by Fact 2.4 that the curve
![]() $\gamma $
deforms in M. In particular, M contains a positive-dimensional family of curves
$\gamma $
deforms in M. In particular, M contains a positive-dimensional family of curves
![]() $\gamma _t$
such that
$\gamma _t$
such that
![]() $M \cdot \gamma _t<0$
. Yet M is a mobile divisor and
$M \cdot \gamma _t<0$
. Yet M is a mobile divisor and
![]() $\dim Y=3$
, so this is impossible.
$\dim Y=3$
, so this is impossible.
Corollary 5.3. In the situation of Setup 1.2, the divisor
![]() $-K_X+M_X$
is nef and has numerical dimension at least three. In particular,
$-K_X+M_X$
is nef and has numerical dimension at least three. In particular,
Proof. By Theorem 2.10, we know that
![]() $-K_X+M_X$
is nef if and only if the restriction to Y is nef. Thus, nefness follows from Proposition 5.2. The numerical dimension is at least three since the restriction to Y is big, so of numerical dimension three. Finally, the vanishing follows from
$-K_X+M_X$
is nef if and only if the restriction to Y is nef. Thus, nefness follows from Proposition 5.2. The numerical dimension is at least three since the restriction to Y is big, so of numerical dimension three. Finally, the vanishing follows from
and the numerical Kawamata-Viehweg vanishing theorem [Reference Lazarsfeld39, Example 4.3.7].
Proposition 5.4. In the situation of Setup 1.2, assume that
![]() $M_X$
is not nef. Then we have
$M_X$
is not nef. Then we have
For the proof, we start with a general lemma which is essentially contained in Küronya’s paper [Reference Küronya38]:
Lemma 5.5. Let Y be a normal projective threefold with canonical Gorenstein singularities, and let D be an effective Cartier divisor on Y such that for every irreducible component
![]() $D' \subset D$
, the restriction
$D' \subset D$
, the restriction
![]() $D|_{D'}$
is pseudoeffective. Then
$D|_{D'}$
is pseudoeffective. Then
unless (maybe) D is nef of numerical dimension at most one.
Proof. Since the restriction
![]() $D|_{D'}$
is pseudoeffective and
$D|_{D'}$
is pseudoeffective and
![]() $\dim D'=2$
, there are at most finitely many curves
$\dim D'=2$
, there are at most finitely many curves
![]() $\gamma \subset Y$
such that
$\gamma \subset Y$
such that
![]() $D \cdot \gamma <0$
. In particular, for a general very ample divisor
$D \cdot \gamma <0$
. In particular, for a general very ample divisor
![]() $A \subset Y$
, the restriction
$A \subset Y$
, the restriction
![]() $D|_A$
is nef. Moreover,
$D|_A$
is nef. Moreover,
and equality holds if and only if the pseudoeffective class
![]() $D|_D$
is zero. Hence, if
$D|_D$
is zero. Hence, if
![]() $(D|_A)^2 =0$
, the restriction
$(D|_A)^2 =0$
, the restriction
![]() $D|_D$
is numerically trivial and D is nef with numerical dimension at most one. If
$D|_D$
is numerically trivial and D is nef with numerical dimension at most one. If
![]() $(D|_A)^2>0$
, the restriction
$(D|_A)^2>0$
, the restriction
![]() $D|_A$
is nef and big and we obtain the vanishing by [Reference Küronya38, Theorem C].Footnote
3
$D|_A$
is nef and big and we obtain the vanishing by [Reference Küronya38, Theorem C].Footnote
3
Proof of Proposition 5.4.
We twist the exact sequence
with
![]() $M_X$
to get
$M_X$
to get
Since M is mobile, it satisfies the conditions of Lemma 5.5; by assumption,
![]() $M_X$
(and thus M) is not nef, so we have
$M_X$
(and thus M) is not nef, so we have
![]() $H^q(Y, {\mathcal O}_Y(M))=0$
for
$H^q(Y, {\mathcal O}_Y(M))=0$
for
![]() $q \geq 2$
. By the exact sequence in cohomology, this implies
$q \geq 2$
. By the exact sequence in cohomology, this implies
Yet the right-hand side vanishes by Corollary 5.3.
Corollary 5.6. In the situation of Setup 1.2, assume that
![]() $M_X$
is not nef. Then the divisor class
$M_X$
is not nef. Then the divisor class
![]() $B_X$
is effective.
$B_X$
is effective.
Proof. We twist the restriction sequence
with
![]() $B_X$
to get
$B_X$
to get
By Serre duality and Proposition 5.4, one has
Therefore,
![]() $h^0(Y, {\mathcal O}_Y(B))=1$
implies that
$h^0(Y, {\mathcal O}_Y(B))=1$
implies that
![]() $B_X$
is effective.
$B_X$
is effective.
Proposition 5.7. In the situation of Setup 1.2, the divisor class
![]() $M_X$
is effective and mobile.
$M_X$
is effective and mobile.
Remark. If
![]() $M_X$
is nef, the linear system
$M_X$
is nef, the linear system
![]() $|M_X|$
might have fixed components. Nevertheless, the class being nef, it is mobile. If
$|M_X|$
might have fixed components. Nevertheless, the class being nef, it is mobile. If
![]() $M_X$
is not nef, the proof will show that
$M_X$
is not nef, the proof will show that
Proof. If
![]() $M_X$
is nef, this is immediate from Lemma 3.7. If
$M_X$
is nef, this is immediate from Lemma 3.7. If
![]() $M_X$
is not nef, we know by Corollary 5.6 that
$M_X$
is not nef, we know by Corollary 5.6 that
![]() $B_X$
is effective. Thus,
$B_X$
is effective. Thus,
![]() $B_X$
is normal prime divisor by Proposition 5.1, and we can twist the restriction sequence for
$B_X$
is normal prime divisor by Proposition 5.1, and we can twist the restriction sequence for
![]() $B_X$
by
$B_X$
by
![]() $K_X+B_X$
to get an exact sequence
$K_X+B_X$
to get an exact sequence
Taking cohomology, we get a sequence
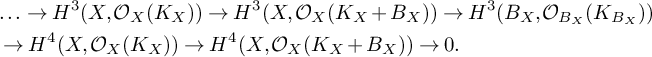 $$ \begin{align*} &\ldots \rightarrow H^3(X, {\mathcal O}_X(K_X)) \rightarrow H^3(X, {\mathcal O}_X(K_X+B_X)) \rightarrow H^3(B_X, {\mathcal O}_{B_X}(K_{B_X})) \\ &\rightarrow H^4(X, {\mathcal O}_X(K_X)) \rightarrow H^4(X, {\mathcal O}_X(K_X+B_X)) \rightarrow 0. \end{align*} $$
$$ \begin{align*} &\ldots \rightarrow H^3(X, {\mathcal O}_X(K_X)) \rightarrow H^3(X, {\mathcal O}_X(K_X+B_X)) \rightarrow H^3(B_X, {\mathcal O}_{B_X}(K_{B_X})) \\ &\rightarrow H^4(X, {\mathcal O}_X(K_X)) \rightarrow H^4(X, {\mathcal O}_X(K_X+B_X)) \rightarrow 0. \end{align*} $$
Using Serre duality on X and
![]() $B_X$
, this transforms into
$B_X$
, this transforms into
 $$ \begin{align*} &\ldots \rightarrow H^1(X, {\mathcal O}_X)=0 \rightarrow H^3(X, {\mathcal O}_X(K_X+B_X)) \rightarrow H^0(B_X, {\mathcal O}_{B_X})=\mathbb{C} \\ &\rightarrow H^0(X, {\mathcal O}_X)=\mathbb{C} \rightarrow H^0(X, {\mathcal O}_X(-B_X))=0 \rightarrow 0. \end{align*} $$
$$ \begin{align*} &\ldots \rightarrow H^1(X, {\mathcal O}_X)=0 \rightarrow H^3(X, {\mathcal O}_X(K_X+B_X)) \rightarrow H^0(B_X, {\mathcal O}_{B_X})=\mathbb{C} \\ &\rightarrow H^0(X, {\mathcal O}_X)=\mathbb{C} \rightarrow H^0(X, {\mathcal O}_X(-B_X))=0 \rightarrow 0. \end{align*} $$
In conclusion, we get
Now we twist the restriction sequence to Y by
![]() $M_X$
to get
$M_X$
to get
By Serre duality and what precedes,
Thus, the restriction map
is surjective. In particular,
Since Y is ample and M is mobile, this shows that
![]() $\dim \mathrm {Bs}(|M_X|) \leq 2$
. Thus,
$\dim \mathrm {Bs}(|M_X|) \leq 2$
. Thus,
![]() $|M_X|$
is mobile.
$|M_X|$
is mobile.
The divisor
![]() $M_X$
being effective by Proposition 5.7, the divisor class
$M_X$
being effective by Proposition 5.7, the divisor class
![]() $-K_X+M_X$
is big. Since
$-K_X+M_X$
is big. Since
![]() $-K_X+M_X$
is also nef by Corollary 5.3, we finally obtain the following:
$-K_X+M_X$
is also nef by Corollary 5.3, we finally obtain the following:
Corollary 5.8. In the situation of Setup 1.2, the divisor
![]() $-K_X+M_X$
is nef and big.
$-K_X+M_X$
is nef and big.
Proposition 5.9. In the situation of Setup 1.2, assume that
![]() $h^0(X, {\mathcal O}_X(B_X)) \neq 0$
. Then the pair
$h^0(X, {\mathcal O}_X(B_X)) \neq 0$
. Then the pair
![]() $(X, B_X)$
is log-canonical. Moreover, the log-canonical centres are the prime divisor
$(X, B_X)$
is log-canonical. Moreover, the log-canonical centres are the prime divisor
![]() $B_{X}$
and (possibly) some smooth curves
$B_{X}$
and (possibly) some smooth curves
![]() $C \subset B_X$
such that
$C \subset B_X$
such that
![]() $B_X \cdot C<0$
.
$B_X \cdot C<0$
.
Proof. We have
![]() $h^0(X, {\mathcal O}_X(B_X)) = 1$
by Proposition 5.1. Thus,
$h^0(X, {\mathcal O}_X(B_X)) = 1$
by Proposition 5.1. Thus,
![]() $B_X$
is the unique effective divisor in its linear system, and hence general. Since
$B_X$
is the unique effective divisor in its linear system, and hence general. Since
![]() $(Y, B) =(Y, Y \cap B_X)$
is log-canonical by Corollary 2.12, we know by Lemma 3.8 that
$(Y, B) =(Y, Y \cap B_X)$
is log-canonical by Corollary 2.12, we know by Lemma 3.8 that
![]() $(X, B_X)$
is lc.
$(X, B_X)$
is lc.
Let us now describe its lc centres: since
![]() $B_X-(K_X+B_X)=-K_X$
is ample, we know by [Reference Fujino17, Theorem 8.1] that for every lc centre
$B_X-(K_X+B_X)=-K_X$
is ample, we know by [Reference Fujino17, Theorem 8.1] that for every lc centre
![]() $Z \subset X$
, the restriction morphism
$Z \subset X$
, the restriction morphism
is surjective. Since
![]() $Z \subset B_X$
and
$Z \subset B_X$
and
![]() $h^0(X, {\mathcal O}_X(B_X))=1$
, we obtain that
$h^0(X, {\mathcal O}_X(B_X))=1$
, we obtain that
![]() $H^0(Z, {\mathcal O}_Z(B_X))=0$
.
$H^0(Z, {\mathcal O}_Z(B_X))=0$
.
This immediately excludes the possibility that
![]() $\dim Z=0$
. Since
$\dim Z=0$
. Since
![]() $B_X$
is normal by Proposition 5.1, there are no two-dimensional lc centres.
$B_X$
is normal by Proposition 5.1, there are no two-dimensional lc centres.
The unique remaining possibility is that
![]() $\dim Z=1$
and the centre is minimal. Thus, by Kawamata subadjunction [Reference Kawamata27], the curve Z is normal and there exists an effective divisor
$\dim Z=1$
and the centre is minimal. Thus, by Kawamata subadjunction [Reference Kawamata27], the curve Z is normal and there exists an effective divisor
![]() $\Delta _Z$
on Z such that
$\Delta _Z$
on Z such that
In particular,
is ample. Thus, if
![]() $B_X \cdot Z \geq 0$
, a Riemann-Roch computation shows that
$B_X \cdot Z \geq 0$
, a Riemann-Roch computation shows that
![]() $h^0(Z, {\mathcal O}_Z(B_X))>0$
, a contradiction.
$h^0(Z, {\mathcal O}_Z(B_X))>0$
, a contradiction.
We now come to the key technical result of this section:
Lemma 5.10. In the situation of Setup 1.2, assume that
![]() $h^0(X, {\mathcal O}_X(B_X)) \neq 0$
. Then we have a surjective restriction morphism
$h^0(X, {\mathcal O}_X(B_X)) \neq 0$
. Then we have a surjective restriction morphism
Proof. By Proposition 5.9, the pair
![]() $(X,B_X)$
is lc, and
$(X,B_X)$
is lc, and
![]() $B_X$
is an lc centre for this pair. By Fujino’s extension theorem [Reference Fujino18, Theorem 1.11], we have to show that
$B_X$
is an lc centre for this pair. By Fujino’s extension theorem [Reference Fujino18, Theorem 1.11], we have to show that
is nef and log big (i.e., the restriction of
![]() $-K_X+M_X$
to every lc centre of
$-K_X+M_X$
to every lc centre of
![]() $(X, B_X)$
is big).
$(X, B_X)$
is big).
By Corollary 5.8, the nef divisor
![]() $-K_X+M_X$
is big on X. Since
$-K_X+M_X$
is big on X. Since
![]() $M_X$
is mobile by Proposition 5.7, the restriction
$M_X$
is mobile by Proposition 5.7, the restriction
![]() $M_X|_{B_X}$
is pseudoeffective, so
$M_X|_{B_X}$
is pseudoeffective, so
![]() $(-K_X+M_X)|_{B_X}$
is big. By Proposition 5.9, an lc centre Z that is distinct from
$(-K_X+M_X)|_{B_X}$
is big. By Proposition 5.9, an lc centre Z that is distinct from
![]() $B_X$
is a curve such that
$B_X$
is a curve such that
![]() $B_X \cdot Z<0$
. Therefore,
$B_X \cdot Z<0$
. Therefore,
![]() $M_X \cdot Z>0$
, and hence
$M_X \cdot Z>0$
, and hence
![]() $(-K_X+M_X)|_{Z}$
, is ample.
$(-K_X+M_X)|_{Z}$
, is ample.
Proposition 5.11. In the situation of Setup 1.2, assume that
![]() $h^0(X, {\mathcal O}_X(B_X)) \neq 0$
. Then we have an injection
$h^0(X, {\mathcal O}_X(B_X)) \neq 0$
. Then we have an injection
Moreover, we have
Proof. We have
![]() $B=Y \cap B_X$
, so
$B=Y \cap B_X$
, so
![]() $B \subset B_X$
is a Cartier divisor that is linearly equivalent to
$B \subset B_X$
is a Cartier divisor that is linearly equivalent to
![]() $-K_X|_{B_X}$
. Thus, we have an exact sequence
$-K_X|_{B_X}$
. Thus, we have an exact sequence
Let us first show that the restriction map
is zero. Since
![]() $B \subset \mathrm {Bs}(|-K_X|)$
, the restriction map
$B \subset \mathrm {Bs}(|-K_X|)$
, the restriction map
is zero. Since
![]() $H^0(X, {\mathcal O}_X(-K_X)) \rightarrow H^0(B_X, {\mathcal O}_{B_X}(-K_X))$
is surjective by Lemma 5.10, we get the claim.
$H^0(X, {\mathcal O}_X(-K_X)) \rightarrow H^0(B_X, {\mathcal O}_{B_X}(-K_X))$
is surjective by Lemma 5.10, we get the claim.
This already implies the second statement since the kernel of the restriction map is
![]() $H^0(B_X, {\mathcal O}_{B_X})=\mathbb {C}$
. Since the restriction map is zero, we have an injection
$H^0(B_X, {\mathcal O}_{B_X})=\mathbb {C}$
. Since the restriction map is zero, we have an injection
Now consider the exact sequence
The pair
![]() $(X, B_X)$
is lc by Proposition 5.9, and
$(X, B_X)$
is lc by Proposition 5.9, and
![]() $B_X$
is normal by Proposition 5.1, so
$B_X$
is normal by Proposition 5.1, so
![]() $B_X$
is a threefold with lc singularities. Since
$B_X$
is a threefold with lc singularities. Since
![]() $K_X|_{B_X}$
is an antiample Cartier divisor, we can apply Kodaira vanishing [Reference Kovács, Schwede and Smith36, Corollary 6.6] to get
$K_X|_{B_X}$
is an antiample Cartier divisor, we can apply Kodaira vanishing [Reference Kovács, Schwede and Smith36, Corollary 6.6] to get
Thus, we have an isomorphism
![]() $H^1(B_X, {\mathcal O}_{B_X}) \simeq H^1(B, {\mathcal O}_B),$
and the first statement follows.
$H^1(B_X, {\mathcal O}_{B_X}) \simeq H^1(B, {\mathcal O}_B),$
and the first statement follows.
Corollary 5.12. In the situation of Setup 1.2, assume that
![]() $h^0(X, {\mathcal O}_X(B_X)) \neq 0$
. Then the pair
$h^0(X, {\mathcal O}_X(B_X)) \neq 0$
. Then the pair
![]() $(X, B_X)$
is plt (i.e., the threefold
$(X, B_X)$
is plt (i.e., the threefold
![]() $B_X$
has canonical Gorenstein singularities).
$B_X$
has canonical Gorenstein singularities).
Proof. By Proposition 5.11, we have
![]() $h^0(B, {\mathcal O}_B(-K_X)) \leq q(B)$
. By Corollary 2.12, the conditions of Lemma 4.2 are satisfied. Thus, we know that B has canonical singularities. By inversion of adjunction (Theorem 2.7), the pair
$h^0(B, {\mathcal O}_B(-K_X)) \leq q(B)$
. By Corollary 2.12, the conditions of Lemma 4.2 are satisfied. Thus, we know that B has canonical singularities. By inversion of adjunction (Theorem 2.7), the pair
![]() $(B_X, B)=(B_X, Y \cap B_X)$
is plt near B. Thus,
$(B_X, B)=(B_X, Y \cap B_X)$
is plt near B. Thus,
![]() $(B_X, 0)$
is plt (i.e., klt) near B. Since
$(B_X, 0)$
is plt (i.e., klt) near B. Since
![]() $B_X$
is Gorenstein, this implies that
$B_X$
is Gorenstein, this implies that
![]() $B_X$
has canonical singularities near B. Since
$B_X$
has canonical singularities near B. Since
![]() $B = B_X \cap Y$
is an ample divisor, the non-canonical locus of
$B = B_X \cap Y$
is an ample divisor, the non-canonical locus of
![]() $B_X$
is at most a finite set.
$B_X$
is at most a finite set.
By Proposition 5.9, the pair
![]() $(X, B_X)$
is lc, and the lc centres of dimension at most two are irreducible curves C. Again by inversion of adjunction, the non-canonical locus of
$(X, B_X)$
is lc, and the lc centres of dimension at most two are irreducible curves C. Again by inversion of adjunction, the non-canonical locus of
![]() $B_X$
coincides with the union of lower-dimensional lc centres which has pure dimension one. By the first paragraph, the non-canonical locus has dimension at most zero, so it is empty.
$B_X$
coincides with the union of lower-dimensional lc centres which has pure dimension one. By the first paragraph, the non-canonical locus has dimension at most zero, so it is empty.
We are now ready for the first reduction step in the proof of Theorem 1.3:
Theorem 5.13. In the situation of Setup 1.2, the divisor
![]() $M_X$
is nef.
$M_X$
is nef.
Proof. We argue by contradiction and assume that
![]() $M_X$
is not nef. By the cone theorem, there exists a
$M_X$
is not nef. By the cone theorem, there exists a
![]() $K_X$
-negative extremal ray
$K_X$
-negative extremal ray
![]() $\mathbb {R}^+ \gamma $
such that
$\mathbb {R}^+ \gamma $
such that
![]() $M_X \cdot \gamma <0$
. Since
$M_X \cdot \gamma <0$
. Since
![]() $M_X$
is mobile by Proposition 5.7, the extremal ray is small. Thus, by Kawamata’s classification [Reference Kawamata26, Theorem 1.1], a connected component of the exceptional locus is a
$M_X$
is mobile by Proposition 5.7, the extremal ray is small. Thus, by Kawamata’s classification [Reference Kawamata26, Theorem 1.1], a connected component of the exceptional locus is a
![]() $\mathbb {P}^2 \subset X$
such that
$\mathbb {P}^2 \subset X$
such that
![]() ${\mathcal O}_{\mathbb {P}^2}(-K_X) \simeq {\mathcal O}_{\mathbb {P}^2}(1)$
. Thus, the intersection
${\mathcal O}_{\mathbb {P}^2}(-K_X) \simeq {\mathcal O}_{\mathbb {P}^2}(1)$
. Thus, the intersection
![]() $Y \cap \mathbb {P}^2$
is either a line or the whole surface
$Y \cap \mathbb {P}^2$
is either a line or the whole surface
![]() $\mathbb {P}^2$
. In the latter case, we would have
$\mathbb {P}^2$
. In the latter case, we would have
![]() $\mathbb {P}^2 \subset M \subset Y$
, in contradiction to the mobility of M. Therefore,
$\mathbb {P}^2 \subset M \subset Y$
, in contradiction to the mobility of M. Therefore,
![]() $Y \cap \mathbb {P}^2$
is a smooth rational curve l such that
$Y \cap \mathbb {P}^2$
is a smooth rational curve l such that
![]() $M \cdot l<0$
. Thus,
$M \cdot l<0$
. Thus,
shows that the effective divisor
![]() $M|_B$
contains a smooth rational curve.
$M|_B$
contains a smooth rational curve.
Since
![]() $M_X$
is not nef, the divisor
$M_X$
is not nef, the divisor
![]() $B_X$
is effective by Corollary 5.6. Thus, Proposition 5.11 implies that we have an injection
$B_X$
is effective by Corollary 5.6. Thus, Proposition 5.11 implies that we have an injection
By Corollary 2.12, the surface B satisfies the conditions of Proposition 4.4. Thus, the support of
![]() $M|_B$
does not contain a smooth rational curve, in contradiction to the first paragraph.
$M|_B$
does not contain a smooth rational curve, in contradiction to the first paragraph.
6 Auxiliary results about linear systems, part II
Theorem 5.13 shows the nefness of the divisor class
![]() $M_X$
which by Fact 2.3 will give us a morphism
$M_X$
which by Fact 2.3 will give us a morphism
![]() $X \rightarrow T$
that adds additional structure to all the varieties appearing in our setup. In this section, we prove further technical results that use these structures.
$X \rightarrow T$
that adds additional structure to all the varieties appearing in our setup. In this section, we prove further technical results that use these structures.
We start with a statement that is a variation of Kollár’s injectivity theorem [Reference Kollár32, Theorem 2.2].
Proposition 6.1. Let Y be a normal
![]() $\mathbb {Q}$
-factorial projective variety with klt singularities such that
$\mathbb {Q}$
-factorial projective variety with klt singularities such that
![]() $c_1(Y)=0$
. Assume that Y admits a fibration
$c_1(Y)=0$
. Assume that Y admits a fibration
![]() $\psi :Y \rightarrow C$
onto a smooth projective curve, and let F be a general fibre. Let A be a nef and big Cartier divisor such that
$\psi :Y \rightarrow C$
onto a smooth projective curve, and let F be a general fibre. Let A be a nef and big Cartier divisor such that
with B an effective divisor such that
![]() $(Y, B)$
is lc. If
$(Y, B)$
is lc. If
![]() $m>1$
, the restriction map
$m>1$
, the restriction map
is surjective.
Proof. It is clearly sufficient to show that
Since Y has klt singularities and
![]() $(Y, B)$
is lc, the pair
$(Y, B)$
is lc, the pair
![]() $(Y, \epsilon B)$
is klt for every
$(Y, \epsilon B)$
is klt for every
![]() $\epsilon < 1$
[Reference Kollár and Mori31, Corollary 2.35(5)]. In particular,
$\epsilon < 1$
[Reference Kollár and Mori31, Corollary 2.35(5)]. In particular,
![]() $(Y, \frac {1}{m} B)$
is klt. Now we write
$(Y, \frac {1}{m} B)$
is klt. Now we write
Since
![]() $A \equiv m (F+\frac {1}{m}B)$
and
$A \equiv m (F+\frac {1}{m}B)$
and
![]() $m>1$
, the
$m>1$
, the
![]() $\mathbb {Q}$
-divisor class
$\mathbb {Q}$
-divisor class
![]() $(m-1) (F+\frac {1}{m}B)$
is nef and big. Now we conclude with Kawamata-Viehweg vanishing [Reference Debarre11, Theorem 7.26].
$(m-1) (F+\frac {1}{m}B)$
is nef and big. Now we conclude with Kawamata-Viehweg vanishing [Reference Debarre11, Theorem 7.26].
Lemma 6.2. Let Y be a normal projective
![]() $\mathbb {Q}$
-factorial threefold with terminal singularities such that
$\mathbb {Q}$
-factorial threefold with terminal singularities such that
![]() $K_Y \simeq {\mathcal O}_Y$
. Suppose that Y admits an elliptic fibration
$K_Y \simeq {\mathcal O}_Y$
. Suppose that Y admits an elliptic fibration
onto a surface T. Let A be a nef and big Cartier divisor such that we have
![]() $A \simeq M + B$
, where
$A \simeq M + B$
, where
![]() $M \simeq \varphi ^* M_T$
with
$M \simeq \varphi ^* M_T$
with
![]() $M_T$
a nef and big Cartier divisor on T and B is an effective divisor such that
$M_T$
a nef and big Cartier divisor on T and B is an effective divisor such that
![]() $B \subset \mathrm {Bs}(|A|)$
.
$B \subset \mathrm {Bs}(|A|)$
.
Then we have an injection
Proof. Since Y is a terminal, Gorenstein,
![]() $\mathbb {Q}$
-factorial threefold, it is factorial [Reference Kawamata25, Lemma 5.1]. Thus, all the Weil divisors on Y are Cartier.
$\mathbb {Q}$
-factorial threefold, it is factorial [Reference Kawamata25, Lemma 5.1]. Thus, all the Weil divisors on Y are Cartier.
Consider the exact sequence
and the long exact sequence in cohomology
By Kawamata-Viehweg vanishing, we have
![]() $H^1(Y, {\mathcal O}_Y(A))=0$
. Since
$H^1(Y, {\mathcal O}_Y(A))=0$
. Since
![]() $B \subset \mathrm {Bs}(|A|)$
, the restriction map
$B \subset \mathrm {Bs}(|A|)$
, the restriction map
![]() $H^0(Y, {\mathcal O}_Y(A)) \rightarrow H^0(B, {\mathcal O}_B(A))$
is zero, so we have an isomorphism
$H^0(Y, {\mathcal O}_Y(A)) \rightarrow H^0(B, {\mathcal O}_B(A))$
is zero, so we have an isomorphism
By the Leray spectral sequence, we have an exact sequence
By the canonical bundle formula [Reference Ambro2], there exists a boundary divisor
![]() $\Delta _T$
on T such that
$\Delta _T$
on T such that
![]() $(T, \Delta _T)$
is klt and
$(T, \Delta _T)$
is klt and
![]() $K_T+\Delta _T \sim _{\mathbb {Q}} 0$
. Since
$K_T+\Delta _T \sim _{\mathbb {Q}} 0$
. Since
![]() $\varphi _* {\mathcal O}_Y(M) \simeq {\mathcal O}_T(M_T)$
is nef and big, we can apply the Kawamata-Viehweg vanishing theorem [Reference Debarre11, Theorem 7.26] to see that
$\varphi _* {\mathcal O}_Y(M) \simeq {\mathcal O}_T(M_T)$
is nef and big, we can apply the Kawamata-Viehweg vanishing theorem [Reference Debarre11, Theorem 7.26] to see that
By the projection formula, we have
so
![]() $R^1 \varphi _* {\mathcal O}_Y(M)$
is torsion-free by [Reference Kollár32, Theorem 2.1].
$R^1 \varphi _* {\mathcal O}_Y(M)$
is torsion-free by [Reference Kollár32, Theorem 2.1].
Since
![]() $K_Y \simeq {\mathcal O}_Y$
and
$K_Y \simeq {\mathcal O}_Y$
and
![]() $\varphi $
is flat over a big open susbset of T, we have by relative duality [Reference Kleiman30]
$\varphi $
is flat over a big open susbset of T, we have by relative duality [Reference Kleiman30]
in the complement of finitely many points. Since
![]() $R^1 \varphi _* {\mathcal O}_Y(M)$
is torsion-free, the morphism
$R^1 \varphi _* {\mathcal O}_Y(M)$
is torsion-free, the morphism
is thus injective and yields an inclusion
The statement now follows from (5).
We need the following characterisation of Example 4.3, a singular variant of [Reference Fujita14, Theorem 0.2] and its proof.
Proposition 6.3. Let S be a normal projective surface with canonical singularities such that
![]() $H^1(S, {\mathcal O}_S) \neq 0$
. Let A be an ample, effective Cartier divisor such that
$H^1(S, {\mathcal O}_S) \neq 0$
. Let A be an ample, effective Cartier divisor such that
![]() $A^2=1$
and
$A^2=1$
and
![]() $K_S \cdot A=-1$
. Then S is a
$K_S \cdot A=-1$
. Then S is a
![]() $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
![]() $f: \mathbb {P}(V) \rightarrow C$
over an elliptic curve C such that A is the tautological divisor.
$f: \mathbb {P}(V) \rightarrow C$
over an elliptic curve C such that A is the tautological divisor.
Proof. Since
![]() $K_S \cdot A=-1$
, the canonical bundle is not pseudoeffective, so S is uniruled. Since
$K_S \cdot A=-1$
, the canonical bundle is not pseudoeffective, so S is uniruled. Since
![]() $H^1(S, {\mathcal O}_S) \neq 0$
, the surface is not rationally connected, and the MRC fibration coincides with the Albanese map
$H^1(S, {\mathcal O}_S) \neq 0$
, the surface is not rationally connected, and the MRC fibration coincides with the Albanese map
![]() $f: S \rightarrow \text {Alb}(S)$
. In particular, f contracts all the rational curves on S and
$f: S \rightarrow \text {Alb}(S)$
. In particular, f contracts all the rational curves on S and
![]() $\pi _1(S) \simeq \pi _1(C)$
, where C is the image of f. Our goal is to show that
$\pi _1(S) \simeq \pi _1(C)$
, where C is the image of f. Our goal is to show that
![]() $q(S)=1$
and f is a
$q(S)=1$
and f is a
![]() $\mathbb {P}^1$
-bundle.
$\mathbb {P}^1$
-bundle.
Since the Cartier divisor A is effective and
![]() $A^2=1$
, the divisor A is an integral curve. By the adjunction formula, the arithmetic genus of A is one, so either A is smooth or its normalisation is
$A^2=1$
, the divisor A is an integral curve. By the adjunction formula, the arithmetic genus of A is one, so either A is smooth or its normalisation is
![]() $\mathbb {P}^1$
. Since the ample divisor A is not contracted by the fibration f, we see that A is a smooth elliptic curve. Now recall that canonical surface singularities are hypersurface singularities, so by Goresky-MacPherson’s Lefschetz theorem for homotopy groups [Reference Lazarsfeld39, Theorem 3.1.21, Remark 3.1.41], the morphism
$\mathbb {P}^1$
. Since the ample divisor A is not contracted by the fibration f, we see that A is a smooth elliptic curve. Now recall that canonical surface singularities are hypersurface singularities, so by Goresky-MacPherson’s Lefschetz theorem for homotopy groups [Reference Lazarsfeld39, Theorem 3.1.21, Remark 3.1.41], the morphism
is surjective; in particular,
![]() $q(S)=1$
and C is also an elliptic curve. Since
$q(S)=1$
and C is also an elliptic curve. Since
is surjective, the étale map map
![]() $A \rightarrow C$
is an isomorphism. Thus, A is a section of f. Since A is ample and has degree one on the fibres, all the f-fibres are integral curves. Thus, f is a
$A \rightarrow C$
is an isomorphism. Thus, A is a section of f. Since A is ample and has degree one on the fibres, all the f-fibres are integral curves. Thus, f is a
![]() $\mathbb {P}^1$
-bundle by [Reference Kollár34, II,Theorem 2.8]. Since
$\mathbb {P}^1$
-bundle by [Reference Kollár34, II,Theorem 2.8]. Since
![]() $A \cdot f=1$
, we have
$A \cdot f=1$
, we have
![]() $S \simeq \mathbb {P}(f_* {\mathcal O}_S(A))$
.
$S \simeq \mathbb {P}(f_* {\mathcal O}_S(A))$
.
Remark 6.4. An elementary computation [Reference Hartshorne20, V, Proposition 2.21] shows that in the situation of Proposition 6.3, the divisor A is adjoint (i.e., we have
with
![]() $\Delta _S$
an ample divisor with
$\Delta _S$
an ample divisor with
![]() $\Delta _S^2=3$
).
$\Delta _S^2=3$
).
Proposition 6.5. Let Z be a normal projective threefold with canonical Gorenstein singularities such that
![]() $q(Z)=1$
and
$q(Z)=1$
and
![]() $-K_Z$
is nef. Let
$-K_Z$
is nef. Let
![]() $S \subset Z$
be a normal surface with canonical singularities such that S is an ample Cartier divisor in Z. Suppose that
$S \subset Z$
be a normal surface with canonical singularities such that S is an ample Cartier divisor in Z. Suppose that
Then either
![]() $K_S \equiv 0$
or S is a ruled surface over an elliptic curve.
$K_S \equiv 0$
or S is a ruled surface over an elliptic curve.
Proof. Let
![]() $\tau :Z' \rightarrow Z$
be a terminalisation of Z. Then
$\tau :Z' \rightarrow Z$
be a terminalisation of Z. Then
![]() $-K_{Z'} \simeq \tau ^* (-K_Z)$
is nef and
$-K_{Z'} \simeq \tau ^* (-K_Z)$
is nef and
![]() $h^i(Z', {\mathcal O}_{Z'})=h^i(Z, {\mathcal O}_Z)$
for all
$h^i(Z', {\mathcal O}_{Z'})=h^i(Z, {\mathcal O}_Z)$
for all
![]() $i \in \mathbb {N}$
. Since
$i \in \mathbb {N}$
. Since
![]() $\tau ^* S \cdot (-K_{Z'})^2 = S \cdot (-K_Z)^2>0$
, the nef divisor
$\tau ^* S \cdot (-K_{Z'})^2 = S \cdot (-K_Z)^2>0$
, the nef divisor
![]() $-K_{Z'}$
is not trivial. Thus,
$-K_{Z'}$
is not trivial. Thus,
![]() $Z'$
is uniruled, and hence,
$Z'$
is uniruled, and hence,
![]() $h^3(Z', {\mathcal O}_{Z'})=0$
. Since
$h^3(Z', {\mathcal O}_{Z'})=0$
. Since
![]() $q(Z)=1$
by assumption, we obtain
$q(Z)=1$
by assumption, we obtain
![]() $\chi (Z', {\mathcal O}_{Z'}) \geq 0$
. Since
$\chi (Z', {\mathcal O}_{Z'}) \geq 0$
. Since
![]() $\tau ^* S$
is nef and big and
$\tau ^* S$
is nef and big and
![]() $-K_{Z'}$
is nef, we have
$-K_{Z'}$
is nef, we have
by Kawamata-Viehweg vanishing. Thus, the Riemann-Roch formula (Fact 2.6) yields
 $$ \begin{align} 1 = h^0(Z', {\mathcal O}_{Z'}(\tau^* S)) &= \chi(Z', {\mathcal O}_{Z'}(\tau^* S)) \\ &\geq \frac{1}{12} \tau^* S \cdot \tau^* (S-K_Z) \cdot \tau^* (2S-K_Z) + \frac{1}{12} \tau^* S \cdot c_2(Z').\nonumber \end{align} $$
$$ \begin{align} 1 = h^0(Z', {\mathcal O}_{Z'}(\tau^* S)) &= \chi(Z', {\mathcal O}_{Z'}(\tau^* S)) \\ &\geq \frac{1}{12} \tau^* S \cdot \tau^* (S-K_Z) \cdot \tau^* (2S-K_Z) + \frac{1}{12} \tau^* S \cdot c_2(Z').\nonumber \end{align} $$
Since
![]() $-K_{Z'}$
is nef and
$-K_{Z'}$
is nef and
![]() $\tau ^* S$
is nef, we have
$\tau ^* S$
is nef, we have
![]() $\tau ^* S \cdot c_2(Z') \geq 0$
by [Reference Ou45, Corollary 1.5]. Applying the projection formula, we obtain
$\tau ^* S \cdot c_2(Z') \geq 0$
by [Reference Ou45, Corollary 1.5]. Applying the projection formula, we obtain
Set
![]() $A:=S|_S$
and
$A:=S|_S$
and
![]() $H=-K_Z|_S$
. Then A is an ample Cartier divisor on S, and H is a nef and big Cartier divisor on S such that
$H=-K_Z|_S$
. Then A is an ample Cartier divisor on S, and H is a nef and big Cartier divisor on S such that
![]() $H^2 \geq 2$
. By the Hodge index inequality
$H^2 \geq 2$
. By the Hodge index inequality
![]() $(A \cdot H)^2 \geq A^2 \cdot H^2$
[Reference Beltrametti and Sommese8, Proposition 2.5.1], this implies
$(A \cdot H)^2 \geq A^2 \cdot H^2$
[Reference Beltrametti and Sommese8, Proposition 2.5.1], this implies
![]() $A \cdot H \geq 2$
. Since
$A \cdot H \geq 2$
. Since
we actually have
![]() $A \cdot H=2$
. Moreover, we have
$A \cdot H=2$
. Moreover, we have
![]() $A^2 \leq 2$
.
$A^2 \leq 2$
.
1st case. Suppose that
![]() $A^2=2$
. Then we have equality in the Hodge index inequality, and therefore,
$A^2=2$
. Then we have equality in the Hodge index inequality, and therefore,
![]() $A \equiv H$
by [Reference Beltrametti and Sommese8, Corollary 2.5.4]. Since
$A \equiv H$
by [Reference Beltrametti and Sommese8, Corollary 2.5.4]. Since
we obtain
![]() $K_S \equiv 0$
.
$K_S \equiv 0$
.
2nd case. Suppose that
![]() $A^2=1$
. Since
$A^2=1$
. Since
we have
![]() $K_S \cdot A=-1$
. Finally, we have the Riemann-Roch inequality
$K_S \cdot A=-1$
. Finally, we have the Riemann-Roch inequality
Since S is an ample divisor in a threefold and Z has canonical singularities, we can use Kodaira vanishing to show that
![]() $q(S)=q(Z)=1$
. In particular,
$q(S)=q(Z)=1$
. In particular,
![]() $\chi ({\mathcal O}_S) \geq 0$
, and by the Riemann-Roch inequality,
$\chi ({\mathcal O}_S) \geq 0$
, and by the Riemann-Roch inequality,
![]() $h^0(S, {\mathcal O}_S(A))>0$
, so A is an effective divisor. Thus, the polarised surface
$h^0(S, {\mathcal O}_S(A))>0$
, so A is an effective divisor. Thus, the polarised surface
![]() $(S, A)$
satisfies the conditions of Proposition 6.3.
$(S, A)$
satisfies the conditions of Proposition 6.3.
7 The nef case
The goal of this section is to show the following.
Theorem 7.1. In the situation of setup 1.2, the divisor
![]() $M_X$
is not nef.
$M_X$
is not nef.
Setup 7.2. For the proof of Theorem 7.1, we will argue by contradiction and assume that
![]() $M_X$
is nef. By the Fact 2.3, there exists a morphism with connected fibres
$M_X$
is nef. By the Fact 2.3, there exists a morphism with connected fibres
such that
![]() $M_ X \simeq \varphi ^* M_T$
for some ample Cartier divisor
$M_ X \simeq \varphi ^* M_T$
for some ample Cartier divisor
![]() $M_T \rightarrow T$
. Note that
$M_T \rightarrow T$
. Note that
![]() $B_X$
is
$B_X$
is
![]() $\varphi $
-ample since
$\varphi $
-ample since
![]() $B_X \sim _\varphi -K_X$
.
$B_X \sim _\varphi -K_X$
.
Since X is a Fano, there exists a boundary divisor such that
![]() $(X, \Delta )$
is klt and
$(X, \Delta )$
is klt and
![]() $\Delta \sim _{\mathbb {Q}} -K_X$
. Thus, we apply Ambro’s theorem [Reference Ambro2] to see that T is klt. Note that it is not clear whether T is
$\Delta \sim _{\mathbb {Q}} -K_X$
. Thus, we apply Ambro’s theorem [Reference Ambro2] to see that T is klt. Note that it is not clear whether T is
![]() $\mathbb {Q}$
-factorial.
$\mathbb {Q}$
-factorial.
Lemma 7.3. In the situation of Setup 7.2, we have
![]() $H^1(X, {\mathcal O}_X(-M_X))=0$
unless
$H^1(X, {\mathcal O}_X(-M_X))=0$
unless
![]() $T \simeq \mathbb {P}^1$
and
$T \simeq \mathbb {P}^1$
and
![]() $M_T \simeq {\mathcal O}_{\mathbb {P}^1}(m)$
with
$M_T \simeq {\mathcal O}_{\mathbb {P}^1}(m)$
with
![]() $m \geq 2$
.
$m \geq 2$
.
Proof. Since
![]() $-K_X$
is
$-K_X$
is
![]() $\varphi $
-ample, we have
$\varphi $
-ample, we have
![]() $R^j \varphi _* {\mathcal O}_X=0$
for every
$R^j \varphi _* {\mathcal O}_X=0$
for every
![]() $j \geq 1$
by relative Kodaira vanishing. Since
$j \geq 1$
by relative Kodaira vanishing. Since
![]() $M_X \simeq \varphi ^* M_T$
, we deduce that
$M_X \simeq \varphi ^* M_T$
, we deduce that
![]() $R^j \varphi _* {\mathcal O}_X(-M_X)=0$
for
$R^j \varphi _* {\mathcal O}_X(-M_X)=0$
for
![]() $j \geq 1$
by the projection formula. Thus, we have
$j \geq 1$
by the projection formula. Thus, we have
and the latter is zero by Kodaira vanishing on the klt space T unless T is a curve. The rest is now straightforward.
Corollary 7.4. In the situation of Setup 7.2, we have
![]() $H^0(X, {\mathcal O}_X(B_X)) \neq 0$
unless
$H^0(X, {\mathcal O}_X(B_X)) \neq 0$
unless
![]() $T \simeq \mathbb {P}^1$
and
$T \simeq \mathbb {P}^1$
and
![]() $M_T \simeq {\mathcal O}_{\mathbb {P}^1}(m)$
with
$M_T \simeq {\mathcal O}_{\mathbb {P}^1}(m)$
with
![]() $m \geq 2$
.
$m \geq 2$
.
Proof. Immediate from Lemma 7.3 and the exact sequence
We will prove Theorem 7.1 by making a case distinction in terms of the dimension of the base T.
Proposition 7.5. In the situation of Setup 7.2, we have
![]() $\dim T> 1$
.
$\dim T> 1$
.
Proof. If
![]() $\dim T=1$
, the fibration
$\dim T=1$
, the fibration
![]() $\varphi $
has as general fibre a smooth Fano threefold F (the divisor
$\varphi $
has as general fibre a smooth Fano threefold F (the divisor
![]() $-K_F \simeq -K_X|_F$
is ample) and
$-K_F \simeq -K_X|_F$
is ample) and
![]() $T \simeq \mathbb {P}^1$
.
$T \simeq \mathbb {P}^1$
.
Choose
![]() $Y \in |-K_X|$
a general element, and denote by
$Y \in |-K_X|$
a general element, and denote by
![]() $\psi :Y \rightarrow \mathbb {P}^1$
the restriction of
$\psi :Y \rightarrow \mathbb {P}^1$
the restriction of
![]() $\varphi $
to Y. Denote by
$\varphi $
to Y. Denote by
![]() $F_Y$
the general
$F_Y$
the general
![]() $\psi $
-fibre; that is,
$\psi $
-fibre; that is,
![]() $F_Y= F \cap Y$
. We have a commutative diagram
$F_Y= F \cap Y$
. We have a commutative diagram

and the horizontal maps are surjective since
![]() $q(X)=0=q(F)$
.
$q(X)=0=q(F)$
.
1st case. Suppose that
![]() ${\mathcal O}_T(M_T) \simeq {\mathcal O}_{\mathbb {P}^1}(m)$
with
${\mathcal O}_T(M_T) \simeq {\mathcal O}_{\mathbb {P}^1}(m)$
with
![]() $m \geq 2$
. We have
$m \geq 2$
. We have
![]() $-K_X|_Y \simeq \psi ^* M_T + B$
; moreover, the pair
$-K_X|_Y \simeq \psi ^* M_T + B$
; moreover, the pair
![]() $(Y,B)$
is lc by Corollary 2.12. Thus, by Proposition 6.1, the restriction map
$(Y,B)$
is lc by Corollary 2.12. Thus, by Proposition 6.1, the restriction map
![]() $r_Y$
is surjective. Since
$r_Y$
is surjective. Since
![]() $-K_X|_Y \simeq \psi ^* M_T + B$
and B is a fixed component of the linear system
$-K_X|_Y \simeq \psi ^* M_T + B$
and B is a fixed component of the linear system
![]() $|-K_X|_Y|$
, the image of
$|-K_X|_Y|$
, the image of
![]() $r_Y$
is generated by a section vanishing on
$r_Y$
is generated by a section vanishing on
![]() $B \cap F_Y$
. Thus,
$B \cap F_Y$
. Thus,
![]() $r_Y$
is a surjective map of rank one, and therefore,
$r_Y$
is a surjective map of rank one, and therefore,
![]() $h^0(F_Y, {\mathcal O}_{F_Y}(-K_X))=1$
. The restriction map
$h^0(F_Y, {\mathcal O}_{F_Y}(-K_X))=1$
. The restriction map
![]() $H^0(F, {\mathcal O}_F(-K_X)) \rightarrow H^0(F_Y, {\mathcal O}_{F_Y}(-K_X))$
has kernel
$H^0(F, {\mathcal O}_F(-K_X)) \rightarrow H^0(F_Y, {\mathcal O}_{F_Y}(-K_X))$
has kernel
![]() $H^0(F, {\mathcal O}_F) \simeq \mathbb {C}$
, so we deduce
$H^0(F, {\mathcal O}_F) \simeq \mathbb {C}$
, so we deduce
![]() $h^0(F, {\mathcal O}_F(-K_X))=2$
. Yet
$h^0(F, {\mathcal O}_F(-K_X))=2$
. Yet
![]() $-K_F \simeq -K_X|_F$
, and for a smooth Fano threefold, we always have
$-K_F \simeq -K_X|_F$
, and for a smooth Fano threefold, we always have
![]() $h^0(F, {\mathcal O}_F(-K_F)) \geq 3$
by [Reference Iskovskikh and Prokhorov24, Corollary 2.1.14].
$h^0(F, {\mathcal O}_F(-K_F)) \geq 3$
by [Reference Iskovskikh and Prokhorov24, Corollary 2.1.14].
2nd case. Suppose that
![]() ${\mathcal O}_T(M_T) \simeq {\mathcal O}_{\mathbb {P}^1}(1)$
. By Corollary 7.4, this implies that
${\mathcal O}_T(M_T) \simeq {\mathcal O}_{\mathbb {P}^1}(1)$
. By Corollary 7.4, this implies that
![]() $B_X$
is an effective divisor. Since
$B_X$
is an effective divisor. Since
![]() $-K_X \simeq \varphi ^* M_T + B_X\simeq F + B_X$
, the divisor
$-K_X \simeq \varphi ^* M_T + B_X\simeq F + B_X$
, the divisor
![]() $B_X$
is relatively ample. We claim that
$B_X$
is relatively ample. We claim that
As in the first case, this yields the surjectivity of
![]() $H^0(Y, {\mathcal O}_Y(-K_X)) \rightarrow H^0(F_Y, {\mathcal O}_{F_Y}(-K_X))$
and the desired contradiction.
$H^0(Y, {\mathcal O}_Y(-K_X)) \rightarrow H^0(F_Y, {\mathcal O}_{F_Y}(-K_X))$
and the desired contradiction.
Proof of the claim. By Proposition 5.1, we know that
![]() $B_X$
is not nef, so there exists a
$B_X$
is not nef, so there exists a
![]() $K_X$
-negative extremal ray
$K_X$
-negative extremal ray
![]() $\mathbb {R}^+ \gamma $
such that
$\mathbb {R}^+ \gamma $
such that
![]() $B_X \cdot \gamma <0$
. Since
$B_X \cdot \gamma <0$
. Since
![]() $B_X$
is effective, the corresponding contraction
$B_X$
is effective, the corresponding contraction
must be birational with exceptional locus contained in
![]() $B_X$
. Since
$B_X$
. Since
![]() $B_X$
is
$B_X$
is
![]() $\varphi $
-ample and
$\varphi $
-ample and
![]() $\mu $
-antiample, the intersection of any
$\mu $
-antiample, the intersection of any
![]() $\mu $
-fibre with a
$\mu $
-fibre with a
![]() $\varphi $
-fibre must be finite. Thus, the fibres of
$\varphi $
-fibre must be finite. Thus, the fibres of
![]() $\mu $
have dimension at most one. By Ando’s theorem [Reference Ando3, Theorem 2.3], this implies that
$\mu $
have dimension at most one. By Ando’s theorem [Reference Ando3, Theorem 2.3], this implies that
![]() $\mu $
is a smooth blowup along a surface. In particular, we have
$\mu $
is a smooth blowup along a surface. In particular, we have
![]() $(-K_X+B_X) \cdot \gamma =0$
, so
$(-K_X+B_X) \cdot \gamma =0$
, so
![]() $-K_X+B_X$
is non-negative on the extremal ray
$-K_X+B_X$
is non-negative on the extremal ray
![]() $\mathbb {R}^+ \gamma $
. Since
$\mathbb {R}^+ \gamma $
. Since
![]() $\gamma $
was an arbitrary
$\gamma $
was an arbitrary
![]() $B_X$
-negative extremal ray, the cone theorem implies that
$B_X$
-negative extremal ray, the cone theorem implies that
![]() $-K_X+B_X$
is nef. Since
$-K_X+B_X$
is nef. Since
![]() $B_X$
is effective, the divisor
$B_X$
is effective, the divisor
![]() $-K_X+B_X$
is nef and big. Therefore,
$-K_X+B_X$
is nef and big. Therefore,
for
![]() $j \geq 1$
by Kawamata-Viehweg vanishing. Now consider the exact sequence
$j \geq 1$
by Kawamata-Viehweg vanishing. Now consider the exact sequence
Since
![]() $M_X \simeq \varphi ^* M_T$
and
$M_X \simeq \varphi ^* M_T$
and
![]() $\dim T=1$
, we have
$\dim T=1$
, we have
![]() $H^2(X, {\mathcal O}_X(-M_X)) \simeq H^2(T, {\mathcal O}_T(-M_T)) = 0.$
By the long exact sequence in cohomology, the map
$H^2(X, {\mathcal O}_X(-M_X)) \simeq H^2(T, {\mathcal O}_T(-M_T)) = 0.$
By the long exact sequence in cohomology, the map
![]() $0=H^1(X, {\mathcal O}_X(B_X)) \rightarrow H^1(Y,{\mathcal O}_Y(B))$
is surjective, and we are finally done.
$0=H^1(X, {\mathcal O}_X(B_X)) \rightarrow H^1(Y,{\mathcal O}_Y(B))$
is surjective, and we are finally done.
Proposition 7.6. In the situation of Setup 7.2, we have
![]() $\dim T < 3$
.
$\dim T < 3$
.
Proof. Assume that
![]() $\dim T \geq 3$
. Since Y is an ample divisor, the morphism
$\dim T \geq 3$
. Since Y is an ample divisor, the morphism
![]() $\varphi |_Y: Y \rightarrow T$
is generically finite onto its image, so
$\varphi |_Y: Y \rightarrow T$
is generically finite onto its image, so
![]() $M \simeq \varphi ^* M_T|_Y$
is nef and big. Consider the exact sequence
$M \simeq \varphi ^* M_T|_Y$
is nef and big. Consider the exact sequence
Since
![]() $H^1(Y, {\mathcal O}_Y(M))=0$
, by Kawamata-Viehweg vanishing, the restriction morphism
$H^1(Y, {\mathcal O}_Y(M))=0$
, by Kawamata-Viehweg vanishing, the restriction morphism
is surjective. Since B is in the base locus of
![]() $|-K_X|_Y|$
, we obtain
$|-K_X|_Y|$
, we obtain
![]() $H^0(B, {\mathcal O}_B(-K_X))=0$
.
$H^0(B, {\mathcal O}_B(-K_X))=0$
.
Since
![]() $\dim\ T \geq 3$
, we have
$\dim\ T \geq 3$
, we have
![]() $h^0(X, {\mathcal O}_X(B_X)) \neq 0$
by Corollary 7.4. Thus, Proposition 5.11 shows that we have an injection
$h^0(X, {\mathcal O}_X(B_X)) \neq 0$
by Corollary 7.4. Thus, Proposition 5.11 shows that we have an injection
By Corollary 2.12, the surface B satisfies the conditions of Proposition 4.2. Thus, we have
![]() $q(B)>0$
, and the inclusion
$q(B)>0$
, and the inclusion
![]() $H^0(B, {\mathcal O}_B(-K_X)) \hookrightarrow H^1(B, {\mathcal O}_B)$
is an equality. Since the first space has dimension zero, this is a contradiction.
$H^0(B, {\mathcal O}_B(-K_X)) \hookrightarrow H^1(B, {\mathcal O}_B)$
is an equality. Since the first space has dimension zero, this is a contradiction.
Proposition 7.7. In the situation of Setup 7.2, we have
![]() $\dim T \neq 2$
$\dim T \neq 2$
This is the part of the proof that requires the most work. We will use properties of the anticanonical divisor Y and the effective divisor
![]() $B_X$
to determine some of the invariants of the base T. Then we will use the smoothness of X to reach a contradiction.
$B_X$
to determine some of the invariants of the base T. Then we will use the smoothness of X to reach a contradiction.
Proof. Assume that
![]() $\dim T=2$
. By Corollary 7.4, the divisor
$\dim T=2$
. By Corollary 7.4, the divisor
![]() $B_X$
is effective. By Corollary 5.12, the divisor
$B_X$
is effective. By Corollary 5.12, the divisor
![]() $B_X$
has canonical Gorenstein singularities, and by Proposition 5.11, we have
$B_X$
has canonical Gorenstein singularities, and by Proposition 5.11, we have
Since
![]() $Y \subset X$
is an ample divisor, the fibration
$Y \subset X$
is an ample divisor, the fibration
![]() $\varphi $
induces an elliptic fibration
$\varphi $
induces an elliptic fibration
such that
![]() $-K_X|_Y \simeq \psi ^* M_T + B$
. By Theorem 2.8 and Corollary 2.9, the threefold Y satisfies the conditions of Lemma 6.2. Hence, we have an injection
$-K_X|_Y \simeq \psi ^* M_T + B$
. By Theorem 2.8 and Corollary 2.9, the threefold Y satisfies the conditions of Lemma 6.2. Hence, we have an injection
Observe that the induced morphism
![]() $\varphi |_{B_X}$
is surjective onto T since
$\varphi |_{B_X}$
is surjective onto T since
![]() $B_X$
is
$B_X$
is
![]() $\varphi $
-ample.
$\varphi $
-ample.
Step 1. We show that
![]() $h^0(T, {\mathcal O}_T(K_T+M_T))=0$
unless
$h^0(T, {\mathcal O}_T(K_T+M_T))=0$
unless
![]() $K_T \simeq -M_T$
. By the adjunction formula,
$K_T \simeq -M_T$
. By the adjunction formula,
is nef with numerical dimension two. Since
![]() $B_X$
has canonical singularities, we can apply [Reference Fujino and Gongyo13, Theorem 3.1] to see that there exists a boundary divisor
$B_X$
has canonical singularities, we can apply [Reference Fujino and Gongyo13, Theorem 3.1] to see that there exists a boundary divisor
![]() $\Delta _T$
on T such that
$\Delta _T$
on T such that
![]() $(T, \Delta _T)$
is klt and
$(T, \Delta _T)$
is klt and
Thus, we have
![]() $K_T+\Delta _T \equiv -M_T$
, and hence,
$K_T+\Delta _T \equiv -M_T$
, and hence,
![]() $K_T+M_T=-\Delta _T$
is not pseudoeffective unless
$K_T+M_T=-\Delta _T$
is not pseudoeffective unless
![]() $\Delta _T=0$
. Therefore,
$\Delta _T=0$
. Therefore,
![]() $h^0(T, {\mathcal O}_T(K_T+M_T)) =0$
unless
$h^0(T, {\mathcal O}_T(K_T+M_T)) =0$
unless
![]() $\Delta _T=0$
. In the latter case,
$\Delta _T=0$
. In the latter case,
![]() $h^0(T, {\mathcal O}_T(K_T+M_T)) \neq 0$
implies that
$h^0(T, {\mathcal O}_T(K_T+M_T)) \neq 0$
implies that
![]() $K_T \simeq -M_T$
; in particular,
$K_T \simeq -M_T$
; in particular,
![]() $K_T$
is Cartier.
$K_T$
is Cartier.
Step 2. We reach a contradiction. By Proposition 5.11, we have an injection
By Corollary 2.12, the surface B satisfies the conditions of Proposition 4.2. In particular, B has canonical singularities, positive irregularity
![]() $q(B)>0$
, and the inclusion above is an equality. Since
$q(B)>0$
, and the inclusion above is an equality. Since
the injection (8) and the first step show that
In particular,
![]() $K_T \simeq -M_T$
by the first step (i.e., T is a del Pezzo surface with at most canonical singularities).
$K_T \simeq -M_T$
by the first step (i.e., T is a del Pezzo surface with at most canonical singularities).
Since B is the complete intersection of
![]() $B_X$
and Y, the surface
$B_X$
and Y, the surface
![]() $B \subset B_X$
is an ample Cartier divisor, and the restriction of
$B \subset B_X$
is an ample Cartier divisor, and the restriction of
![]() $\varphi |_{B_X}$
to B is still surjective onto the surface T. Since
$\varphi |_{B_X}$
to B is still surjective onto the surface T. Since
![]() $q(T)=0$
and
$q(T)=0$
and
![]() $q(B)=1$
, and the irregularity is a birational invariant of varieties with rational singularities, the map
$q(B)=1$
, and the irregularity is a birational invariant of varieties with rational singularities, the map
is not birational. Thus,
![]() $\tau $
is generically finite of degree at least two and
$\tau $
is generically finite of degree at least two and
Thus,
![]() $q(B_X)=q(B)=1$
,
$q(B_X)=q(B)=1$
,
![]() $-K_{B_X} \simeq M_X|_{B_X}$
is nef,
$-K_{B_X} \simeq M_X|_{B_X}$
is nef,
![]() $B\subset B_X$
is an ample Cartier divisor with
$B\subset B_X$
is an ample Cartier divisor with
![]() $h^0(B_X, {\mathcal O}_{B_X}(B))=h^0(B_X, {\mathcal O}_{B_X}(-K_X))=1$
and
$h^0(B_X, {\mathcal O}_{B_X}(B))=h^0(B_X, {\mathcal O}_{B_X}(-K_X))=1$
and
![]() $B\cdot (-K_{B_X})^2\geq 2$
. Thus, the threefold
$B\cdot (-K_{B_X})^2\geq 2$
. Thus, the threefold
![]() $B_X$
and the surface
$B_X$
and the surface
![]() $B \subset B_X$
satisfy the conditions of Proposition 6.5, and we have two cases:
$B \subset B_X$
satisfy the conditions of Proposition 6.5, and we have two cases:
Case a) We have
![]() $K_B \equiv 0$
. Since
$K_B \equiv 0$
. Since
![]() $K_B \simeq B|_B$
, this implies that B is nef. Thus,
$K_B \simeq B|_B$
, this implies that B is nef. Thus,
![]() $B_X$
is nef by Theorem 2.10, a contradiction to Proposition 5.1.
$B_X$
is nef by Theorem 2.10, a contradiction to Proposition 5.1.
Case b) B is a ruled surface over an elliptic curve. Since
![]() $\rho (\mathbb {P}(V))=2$
and the map
$\rho (\mathbb {P}(V))=2$
and the map
![]() $\tau $
is surjective, the del Pezzo surface T has Picard number at most two (canonical singularities are
$\tau $
is surjective, the del Pezzo surface T has Picard number at most two (canonical singularities are
![]() $\mathbb {Q}$
-factorial, [Reference Kollár and Mori31, Proposition 4.11]). By Remark 6.4, the nef and big class
$\mathbb {Q}$
-factorial, [Reference Kollár and Mori31, Proposition 4.11]). By Remark 6.4, the nef and big class
![]() $M_X|_B$
is ample and
$M_X|_B$
is ample and
![]() $(M_X|_B)^2=3$
. Since
$(M_X|_B)^2=3$
. Since
![]() $M_X|_B \simeq \tau ^* M_T \simeq \tau ^* (-K_T)$
is ample, the generically finite map
$M_X|_B \simeq \tau ^* M_T \simeq \tau ^* (-K_T)$
is ample, the generically finite map
![]() $\tau $
is actually finite. Moreover,
$\tau $
is actually finite. Moreover,
![]() $\tau $
having degree at least two, we deduce that
$\tau $
having degree at least two, we deduce that
![]() $\tau $
has degree three and
$\tau $
has degree three and
![]() $(-K_T)^2=1$
. Thus, T is a del Pezzo surface of degree one and Picard number at most two; in particular, it is not smooth. By [Reference Andreatta and Wiśniewski4, Proposition 1.3], this implies that the fibration
$(-K_T)^2=1$
. Thus, T is a del Pezzo surface of degree one and Picard number at most two; in particular, it is not smooth. By [Reference Andreatta and Wiśniewski4, Proposition 1.3], this implies that the fibration
![]() $\varphi :X \rightarrow T$
is not equidimensional, so there exists a prime divisor
$\varphi :X \rightarrow T$
is not equidimensional, so there exists a prime divisor
![]() $D \subset X$
that is contracted onto a point in T.
$D \subset X$
that is contracted onto a point in T.
Since the effective divisors
![]() $B_X$
and Y are
$B_X$
and Y are
![]() $\varphi $
-ample, the intersection
$\varphi $
-ample, the intersection
is non-empty. Hence, there exists a curve
![]() $E \subset B$
that is contracted by
$E \subset B$
that is contracted by
![]() $\tau $
. Yet we showed above that
$\tau $
. Yet we showed above that
![]() $\tau $
is finite, a contradiction.
$\tau $
is finite, a contradiction.
Remark. It may seem annoying that the case of a fibration
![]() $X \rightarrow T$
with T a del Pezzo surface of degree one requires so much additional effort. Note, however, that this situation is very close to Example 3.2, so our arguments must be specific enough to rule out this situation.
$X \rightarrow T$
with T a del Pezzo surface of degree one requires so much additional effort. Note, however, that this situation is very close to Example 3.2, so our arguments must be specific enough to rule out this situation.
Acknowledgements
A.H. thanks the Institut Universitaire de France for providing excellent working conditions for this project. S.A.S. thanks the LJAD Université Côte d’Azur for partially funding his long stay in Nice, in order to establish this project; he also thanks the Mathematics Department of the University of Turin for the opportunities given during his PhD. We thank the referee for the careful verification of our arguments.


