Article contents
THE METRIC PROJECTIONS ONTO CLOSED CONVEX CONES IN A HILBERT SPACE
Published online by Cambridge University Press: 11 February 2021
Abstract
We study the metric projection onto the closed convex cone in a real Hilbert space 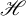 $\mathscr {H}$ generated by a sequence
$\mathscr {H}$ generated by a sequence 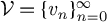 $\mathcal {V} = \{v_n\}_{n=0}^\infty $. The first main result of this article provides a sufficient condition under which the closed convex cone generated by
$\mathcal {V} = \{v_n\}_{n=0}^\infty $. The first main result of this article provides a sufficient condition under which the closed convex cone generated by 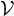 $\mathcal {V}$ coincides with the following set:
$\mathcal {V}$ coincides with the following set: 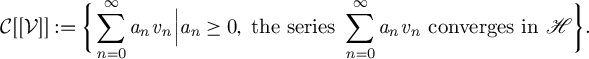
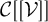 $\mathcal {C}[[\mathcal {V}]]$. As an application, we obtain the best approximations of many concrete functions in
$\mathcal {C}[[\mathcal {V}]]$. As an application, we obtain the best approximations of many concrete functions in 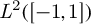 $L^2([-1,1])$ by polynomials with nonnegative coefficients.
$L^2([-1,1])$ by polynomials with nonnegative coefficients.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 5 , September 2022 , pp. 1617 - 1650
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by


