1. Introduction
Various Henselian valued fields are amenable to model theoretic study. Those include the p-adic numbers (more generally, p-adically closed fields) and (non-trivially) valued real closed and algebraically closed fields, as well as various expansions thereof (e.g., by restricted analytic functions). Recently, a new axiomatic framework for tame valued fields (of characteristic
![]() $0$
) was introduced. This framework, known as Hensel-minimality,Footnote 1 was suggested in [Reference Cluckers, Halupczok and Rideau-Kikuchi4] and [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5] as a valued field analogue of o-minimality. The notion of
$0$
) was introduced. This framework, known as Hensel-minimality,Footnote 1 was suggested in [Reference Cluckers, Halupczok and Rideau-Kikuchi4] and [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5] as a valued field analogue of o-minimality. The notion of
![]() $1$
-h-minimality is both broad and powerful. Known examples include, among others, all pure Henselian valued fields of characteristic
$1$
-h-minimality is both broad and powerful. Known examples include, among others, all pure Henselian valued fields of characteristic
![]() $0$
as well as their expansions by restricted analytic functions. Known tameness consequences of
$0$
as well as their expansions by restricted analytic functions. Known tameness consequences of
![]() $1$
-h-minimality include a well-behaved dimension theory and strong regularity of definable functions (e.g., a generic Taylor approximation theorem for definable functions).
$1$
-h-minimality include a well-behaved dimension theory and strong regularity of definable functions (e.g., a generic Taylor approximation theorem for definable functions).
In the present paper, we initiate a study of groups definable in
![]() $1$
-h-minimal fields. Using the above-mentioned tameness and regularity conditions provided by
$1$
-h-minimal fields. Using the above-mentioned tameness and regularity conditions provided by
![]() $1$
-h-minimality and inspired by similar studies in the o-minimal setting (initiated in [Reference Pillay11]) and in p-adically closed fields ([Reference Pillay12]), our first theorem (Proposition 6.4, stated here in a slightly weaker form) is as follows:
$1$
-h-minimality and inspired by similar studies in the o-minimal setting (initiated in [Reference Pillay11]) and in p-adically closed fields ([Reference Pillay12]), our first theorem (Proposition 6.4, stated here in a slightly weaker form) is as follows:
Theorem 1. Let K be a
![]() $1$
-h-minimal field and G be an infinite group definable in K. Then G admits a definable weak
$1$
-h-minimal field and G be an infinite group definable in K. Then G admits a definable weak
![]() ${\mathcal C}^k$
(any k) manifold structure with respect to which G has the structure of a strictly differentiable weak
${\mathcal C}^k$
(any k) manifold structure with respect to which G has the structure of a strictly differentiable weak
![]() ${\mathcal C}^k$
-Lie group. More precisely, the forgetful functor from definable strictly differentiable weak Lie groups to definable groups is an equivalence of categories. If algebraic closure coincides with definable closure in K, then a definable weak Lie group is a definable Lie group.
${\mathcal C}^k$
-Lie group. More precisely, the forgetful functor from definable strictly differentiable weak Lie groups to definable groups is an equivalence of categories. If algebraic closure coincides with definable closure in K, then a definable weak Lie group is a definable Lie group.
Above, by a definable weak Lie group (over K), we mean a Lie group whose underlying K-manifold structure may not have a definable (so, in particular, finite) atlas but can be covered by (the domains of) finitely many compatible étale maps. We do not know whether this is a necessary requirement for the correctness of the statement, or an artifact of the proof: we follow Pillay’s argument in the o-minimal and p-adic contexts ([Reference Pillay11], [Reference Pillay12]), but the fact that, in the present setting, finite covers are not generically trivial requires that we work with weakly definable manifolds, in the above sense. To pursue this argument, we have to extend the study of definable functions beyond what was done in [Reference Cluckers, Halupczok and Rideau-Kikuchi4] (and its sequel). Specifically, instead of working with continuously differentiable functions (as is the case in the o-minimal setting), we are working with strictly differentiable functions, and for those we prove an inverse function theorem, allowing us to deduce an implicit function theorem for definable functions as well as other standard consequences of these theorems. This allows us to develop the basic theory of the category of (weak) manifolds definable in this setting. Among others, we prove a definable version of Sard’s Lemma.
We do not know whether strict differentiability follows in the
![]() $1$
-h-minimal context from continuous differentiability (as is the case in real analysis), but it can be easily inferred from a multi-variable Taylor approximation theorem for definable functions available in this context.
$1$
-h-minimal context from continuous differentiability (as is the case in real analysis), but it can be easily inferred from a multi-variable Taylor approximation theorem for definable functions available in this context.
Having established that definable groups are Lie, our next theorem establishes the natural Lie correspondence (asserting that the germ of a definable group morphism at the identity is determined by its derivative at that point). For applications, it is convenient to state the result for local groups (Corollary 6.11):
Theorem 2. Let K be a
![]() $1$
-h-minimal field, U and V definable strictly differentiable local Lie groups and
$1$
-h-minimal field, U and V definable strictly differentiable local Lie groups and
![]() $g,f:U\to V$
definable strictly differentiable local Lie group morphisms. If we denote
$g,f:U\to V$
definable strictly differentiable local Lie group morphisms. If we denote
![]() $Z=\{x\in U: g(x)=f(x)\}$
, then
$Z=\{x\in U: g(x)=f(x)\}$
, then
![]() $\dim _e Z=\dim (\ker (f'(e)-g'(e)))$
, where e denotes the identity of the local group U.
$\dim _e Z=\dim (\ker (f'(e)-g'(e)))$
, where e denotes the identity of the local group U.
We then prove two applications. First, we show – adapting techniques from the o-minimal context – that every infinite field definable in a
![]() $1$
-h-minimal field K is definably isomorphic to a finite extension of K, Proposition 7.3. This generalises an analogous result for real closed valued fields ([Reference Bays and Peterzil2]) and p-adically closed fields ([Reference Pillay12]). It will be interesting to know whether these results can be extended to interpretable fields (in the spirit of [Reference Halevi, Hasson and Peterzil6] or [Reference Hrushovski and Rideau-Kikuchi9, §6] under suitable additional assumptions on the RV-sort.
$1$
-h-minimal field K is definably isomorphic to a finite extension of K, Proposition 7.3. This generalises an analogous result for real closed valued fields ([Reference Bays and Peterzil2]) and p-adically closed fields ([Reference Pillay12]). It will be interesting to know whether these results can be extended to interpretable fields (in the spirit of [Reference Halevi, Hasson and Peterzil6] or [Reference Hrushovski and Rideau-Kikuchi9, §6] under suitable additional assumptions on the RV-sort.
Our next application is a proof that definable
![]() $1$
-dimensional groups are finite-by-abelian-by-finite, Corollary 8.10. This generalises analogous results in the o-minimal context ([Reference Pillay11]), in p-adically closed fields ([Reference Pillay12]) and combines with [Reference Acosta1] to give a complete classification of
$1$
-dimensional groups are finite-by-abelian-by-finite, Corollary 8.10. This generalises analogous results in the o-minimal context ([Reference Pillay11]), in p-adically closed fields ([Reference Pillay12]) and combines with [Reference Acosta1] to give a complete classification of
![]() $1$
-dimensional groups definable in ACVF
$1$
-dimensional groups definable in ACVF
![]() $_0$
.
$_0$
.
The present paper is a first step toward the study of groups definable in
![]() $1$
-h-minimal fields. It seems that more standard results on Lie groups over complete local fields can be extended to this context. Thus, for example, it can be shown that any definable local group contains a definable open subgroup. As the proof is long and involves new techniques, we postpone it to a subsequent paper.
$1$
-h-minimal fields. It seems that more standard results on Lie groups over complete local fields can be extended to this context. Thus, for example, it can be shown that any definable local group contains a definable open subgroup. As the proof is long and involves new techniques, we postpone it to a subsequent paper.
1.1. Structure of the paper
In Section 2, we review the basics of
![]() $1$
-h-minimality and dimension theory in geometric structures. In Section 3, we prove a multi-variable Taylor approximation theorem for
$1$
-h-minimality and dimension theory in geometric structures. In Section 3, we prove a multi-variable Taylor approximation theorem for
![]() $1$
-h-minimal fields, and we formulate some strong regularity conditions (implied, generically, by Taylor’s theorem) that will be needed in later parts of the paper. These results are probably known to the experts, and we include them mostly for the sake of completeness and clarity of exposition (as some of them do not seem to exist in writing).
$1$
-h-minimal fields, and we formulate some strong regularity conditions (implied, generically, by Taylor’s theorem) that will be needed in later parts of the paper. These results are probably known to the experts, and we include them mostly for the sake of completeness and clarity of exposition (as some of them do not seem to exist in writing).
In Section 4, we prove the inverse function theorem and related theorems on the local structure of immersions, submersions and constant rank functions. Though some proofs are similar to those of analogous statements in real analysis (and, more generally, in the o-minimal context), this is not true throughout. Specifically,
![]() $1$
-h-minimality is invoked in a crucial way in the proof that a function with vanishing derivative is locally constant, which, in turn, is used in our proof of the Lie correspondence for definable groups.
$1$
-h-minimality is invoked in a crucial way in the proof that a function with vanishing derivative is locally constant, which, in turn, is used in our proof of the Lie correspondence for definable groups.
In Section 5, we introduce several versions of definable manifolds in
![]() $1$
-h-minimal fields, and we develop their basic theory.
$1$
-h-minimal fields, and we develop their basic theory.
Using the results of the first sections, our study of definable groups starts in Section 6. We first show that definable groups can be endowed with an essentially unique strictly differentiable weak Lie group structure and that the germ of definable group morphisms are determined by their derivative at the identity. We then define the (definable) Lie algebra associated with a definable Lie group, and show that it satisfies the familiar properties of Lie algebras. This is done using a local computation, after characterising the Lie bracket as the second order part of the commutator function near the identity.
Section 7 is dedicated to the classification of fields definable in
![]() $1$
-h-minimal fields, and in Section 8, we prove our results on definable one-dimensional groups.
$1$
-h-minimal fields, and in Section 8, we prove our results on definable one-dimensional groups.
2. Preliminaries
In this section, we describe some background definitions, notation and basic relevant results, used in later sections. Most of the terminology below is either standard or taken from [Reference Cluckers, Halupczok and Rideau-Kikuchi4]. Throughout, K will denote a non-trivially valued field. We will not distinguish notationally between the structure and its universe. Formally, we allow K to be a multi-sorted structure (with all sorts coming from
![]() $K^{eq}$
), but by a definable set we mean, unless explicitly stated otherwise, a subset of
$K^{eq}$
), but by a definable set we mean, unless explicitly stated otherwise, a subset of
![]() $K^n$
definable with parameters. All tuples are finite, and we write (as is common in model theory)
$K^n$
definable with parameters. All tuples are finite, and we write (as is common in model theory)
![]() $a\in K$
for
$a\in K$
for
![]() $a\in K^n$
, where
$a\in K^n$
, where
![]() $n=\mathrm {length}(a)$
. We apply the same convention to variables.
$n=\mathrm {length}(a)$
. We apply the same convention to variables.
To stress the analogy of the current setting with the Real numbers, we use multiplicative notation for the valuation. Thus, the valued group is denoted
![]() $(\Gamma ,\cdot )$
and the valuation
$(\Gamma ,\cdot )$
and the valuation
![]() $|\cdot |:K\to \Gamma _0=\Gamma \cup \{0\}$
, and if
$|\cdot |:K\to \Gamma _0=\Gamma \cup \{0\}$
, and if
![]() $x\in K^n$
, we set
$x\in K^n$
, we set
![]() $|x|:=\max _{1\leq k\leq n}|x_k|$
.
$|x|:=\max _{1\leq k\leq n}|x_k|$
.
An open ball of (valuative) radius
![]() $r\in \Gamma $
in
$r\in \Gamma $
in
![]() $K^n$
is a set of the form
$K^n$
is a set of the form
![]() $B=\{x\in K^n: |x-a|<r\}$
for
$B=\{x\in K^n: |x-a|<r\}$
for
![]() $a\in K^n$
. The balls endow K with a field topology (the valuation topology). Up until Section 5, all topological notions mentioned in the text will refer solely to this topology and the product topology it induces on
$a\in K^n$
. The balls endow K with a field topology (the valuation topology). Up until Section 5, all topological notions mentioned in the text will refer solely to this topology and the product topology it induces on
![]() $K^n$
.
$K^n$
.
We denote
![]() $\mathcal {O}:=\{x: |x|\le 1\}$
, the valuation ring,
$\mathcal {O}:=\{x: |x|\le 1\}$
, the valuation ring,
![]() $\mathcal {M}:=\{x\in {\mathcal O}: |x|<1\}$
, the valuation ideal, and
$\mathcal {M}:=\{x\in {\mathcal O}: |x|<1\}$
, the valuation ideal, and
![]() $k:={\mathcal O}/{\mathcal M}$
, the residue field. We also denote
$k:={\mathcal O}/{\mathcal M}$
, the residue field. We also denote
![]() $RV=K^{\times }/(1+\mathcal {M})$
. More generally, whenever
$RV=K^{\times }/(1+\mathcal {M})$
. More generally, whenever
![]() $s\in \Gamma $
and
$s\in \Gamma $
and
![]() $s\leq 1$
, we denote
$s\leq 1$
, we denote
![]() $\mathcal {M}_s=\{x\in K: |x|<s\}$
, and
$\mathcal {M}_s=\{x\in K: |x|<s\}$
, and
![]() $RV_s=K^{\times }/(1+\mathcal {M}_s)$
. If K has mixed characteristic
$RV_s=K^{\times }/(1+\mathcal {M}_s)$
. If K has mixed characteristic
![]() $(0,p)$
, we denote
$(0,p)$
, we denote
![]() $RV_{p,n}=RV_{|p|^n}$
and
$RV_{p,n}=RV_{|p|^n}$
and
![]() $RV_{p,\bullet }=\bigcup _n RV_{p,n}$
.
$RV_{p,\bullet }=\bigcup _n RV_{p,n}$
.
It is convenient, when discussing approximation theorems, to adopt the big-O notation from real analysis. For the sake of clarity, we recall this notation in the valued field setting:
Definition 2.1.
-
(1) If
 $f:U\to K^m$
and
$f:U\to K^m$
and
 $g:U\to \Gamma _0$
are functions defined in an open neighborhood of
$g:U\to \Gamma _0$
are functions defined in an open neighborhood of
 $0$
in
$0$
in
 $K^n$
, then
$K^n$
, then
 $f(x)=O(g(x))$
means that there are
$f(x)=O(g(x))$
means that there are
 $r, M>0$
in
$r, M>0$
in
 $\Gamma $
, such that if
$\Gamma $
, such that if
 $|x|<r$
, then
$|x|<r$
, then
 $|f(x)|\le Mg(x)$
. We also denote
$|f(x)|\le Mg(x)$
. We also denote
 $f_1(x)=f_2(x)+O(g(x))$
if
$f_1(x)=f_2(x)+O(g(x))$
if
 $f_1(x)-f_2(x)=O(g(x))$
.
$f_1(x)-f_2(x)=O(g(x))$
. -
(2) If
 $g:U\to K^r$
, and
$g:U\to K^r$
, and
 $s\in \mathbb {N}$
, then
$s\in \mathbb {N}$
, then
 $O(g(x)^s)=O(|g(x)|^s)$
.
$O(g(x)^s)=O(|g(x)|^s)$
. -
(3) If
 $f:Y\times U\to K^m$
is a function where U is an open neighborhood of
$f:Y\times U\to K^m$
is a function where U is an open neighborhood of
 $0$
in
$0$
in
 $K^n$
, and if
$K^n$
, and if
 $g:U\to \Gamma _0$
, then
$g:U\to \Gamma _0$
, then
 $f(y,x)=O_y(g(x))$
means that for every
$f(y,x)=O_y(g(x))$
means that for every
 $y\in Y$
, there are
$y\in Y$
, there are
 $r_y,M_y>0$
, such that if
$r_y,M_y>0$
, such that if
 $|x|<r_y$
, then
$|x|<r_y$
, then
 $|f(y,x)|\le M_yg(x)$
.
$|f(y,x)|\le M_yg(x)$
.
As mentioned in the introduction, in the present paper, we are working with the notion of strict differentiability that we now recall:
Definition 2.2. Let
![]() $U\subset K^n$
be an open subset and
$U\subset K^n$
be an open subset and
![]() $f:U\to K^m$
be a map. Then f is strictly differentiable at
$f:U\to K^m$
be a map. Then f is strictly differentiable at
![]() $a\in U$
if there is a linear map
$a\in U$
if there is a linear map
![]() $A:K^n\to K^m$
such that for every
$A:K^n\to K^m$
such that for every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\delta>0$
satisfying
$\delta>0$
satisfying
![]() $|f(x)-f(y)-A(x-y)|\leq \epsilon |x-y|$
for every
$|f(x)-f(y)-A(x-y)|\leq \epsilon |x-y|$
for every
![]() $x,y$
such that
$x,y$
such that
![]() $|x-a|<\delta $
and
$|x-a|<\delta $
and
![]() $|y-a|<\delta $
.
$|y-a|<\delta $
.
f is strictly differentiable in U if it is strictly differentiable at every point of U.
In the situation of the definition, the linear map A is uniquely determined and denoted
![]() $f'(a)$
. If f is strictly differentiable in an open U, then it is continuously differentiable.
$f'(a)$
. If f is strictly differentiable in an open U, then it is continuously differentiable.
Definition 2.3. Let
![]() $U\subset K^n$
and
$U\subset K^n$
and
![]() $V\subset K^n$
be open subsets. Then
$V\subset K^n$
be open subsets. Then
![]() $f:U\to V$
is a strict diffeomorphism if it is strictly differentiable and bijective and if its inverse is strictly differentiable.
$f:U\to V$
is a strict diffeomorphism if it is strictly differentiable and bijective and if its inverse is strictly differentiable.
As we will see, a strict diffeomorphism is just a strictly differentiable diffeomorphism.
Given an open ball
![]() $B\subseteq K^n$
of radius r, a subset Y of
$B\subseteq K^n$
of radius r, a subset Y of
![]() $K^n$
, and an element
$K^n$
, and an element
![]() $s\in \Gamma $
with
$s\in \Gamma $
with
![]() $s\leq 1$
, we say that B is s-away from Y if
$s\leq 1$
, we say that B is s-away from Y if
![]() $B'\cap Y=\emptyset $
for
$B'\cap Y=\emptyset $
for
![]() $B'$
the open ball of radius
$B'$
the open ball of radius
![]() $s^{-1}r$
containing B. Note the closely related definition in [Reference Cluckers, Halupczok and Rideau-Kikuchi4] of a ball
$s^{-1}r$
containing B. Note the closely related definition in [Reference Cluckers, Halupczok and Rideau-Kikuchi4] of a ball
![]() $B\subset K$
being s-next to a finite set
$B\subset K$
being s-next to a finite set
![]() $Y\subset K$
. In that terminology, a ball B is s-next to Y if it is maximal among the balls s-away from Y.
$Y\subset K$
. In that terminology, a ball B is s-next to Y if it is maximal among the balls s-away from Y.
Note that every point not in the closure of Y is contained in a ball s-away from Y. This is because if B is an open ball of radius r disjoint from Y, then every open ball of radius
![]() $sr$
contained in B is s-away from Y.
$sr$
contained in B is s-away from Y.
Following [Reference Cluckers, Halupczok and Rideau-Kikuchi4], we say that a finite set
![]() $Y\subset K$
prepares the set
$Y\subset K$
prepares the set
![]() $X\subset K$
if every ball B disjoint from Y is either disjoint from X or contained in X. More generally, if
$X\subset K$
if every ball B disjoint from Y is either disjoint from X or contained in X. More generally, if
![]() $s\in \Gamma $
is such that
$s\in \Gamma $
is such that
![]() $s\leq 1$
, then Y s-prepares X if every open ball B s-away from Y is either contained in X or disjoint from X.
$s\leq 1$
, then Y s-prepares X if every open ball B s-away from Y is either contained in X or disjoint from X.
If K is a valued field of mixed characteristic
![]() $(0,p)$
, given an integer
$(0,p)$
, given an integer
![]() $m\in \mathbb {N}$
, an open ball,
$m\in \mathbb {N}$
, an open ball,
![]() $B\subseteq K^n$
and a set
$B\subseteq K^n$
and a set
![]() $Y\subseteq K^n$
, we say that B is m-away from Y if it is
$Y\subseteq K^n$
, we say that B is m-away from Y if it is
![]() $|p|^m$
-away from Y. Similarly, if
$|p|^m$
-away from Y. Similarly, if
![]() $s\in \Gamma $
and
$s\in \Gamma $
and
![]() $s\leq 1$
, then B is m-s-away from Y if it is
$s\leq 1$
, then B is m-s-away from Y if it is
![]() $|p|^ms$
-away from Y. Given a finite
$|p|^ms$
-away from Y. Given a finite
![]() $Y\subset K$
and
$Y\subset K$
and
![]() $X\subset K$
, we say that Y m-prepares (resp. m-s-prepares) the set X if Y
$X\subset K$
, we say that Y m-prepares (resp. m-s-prepares) the set X if Y
![]() $|p|^m$
-prepares X (resp. Y
$|p|^m$
-prepares X (resp. Y
![]() $|p|^ms$
-prepares X).
$|p|^ms$
-prepares X).
Next, we recall the definitions of 1-h-minimality defined in the equi-characteristic
![]() $0$
([Reference Cluckers, Halupczok and Rideau-Kikuchi4]) and in the mixed characteristic ([Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5]) settings:
$0$
([Reference Cluckers, Halupczok and Rideau-Kikuchi4]) and in the mixed characteristic ([Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5]) settings:
Definition 2.4. Let K be an
![]() $\aleph _0$
-saturated non-trivially valued field of characteristic
$\aleph _0$
-saturated non-trivially valued field of characteristic
![]() $0$
, which is a structure in a language expanding the language of valued fields.
$0$
, which is a structure in a language expanding the language of valued fields.
-
(1) If K has residue characteristic
 $0$
, then K is
$0$
, then K is
 $1$
-h-minimal, if for any
$1$
-h-minimal, if for any
 $s\le 1$
in
$s\le 1$
in
 $\Gamma $
any
$\Gamma $
any
 $A\subseteq K$
,
$A\subseteq K$
,
 $A'\in RV_s$
(a singleton) and every
$A'\in RV_s$
(a singleton) and every
 $(A\cup RV\cup A')$
-definable set
$(A\cup RV\cup A')$
-definable set
 $X\subset K$
, there is an A-definable finite set
$X\subset K$
, there is an A-definable finite set
 $Y\subset K$
s-preparing X.
$Y\subset K$
s-preparing X. -
(2) If K has mixed characteristic
 $(0,p)$
, then K is
$(0,p)$
, then K is
 $1$
-h-minimal, if for any
$1$
-h-minimal, if for any
 $s\le 1$
in
$s\le 1$
in
 $\Gamma $
any
$\Gamma $
any
 $A\subseteq K$
,
$A\subseteq K$
,
 $A'\in RV_{s}$
(a singleton) and every
$A'\in RV_{s}$
(a singleton) and every
 $(A\cup RV_{p,\bullet }\cup A')$
-definable set
$(A\cup RV_{p,\bullet }\cup A')$
-definable set
 $X\subset K$
, there is
$X\subset K$
, there is
 $m\in {\mathbb {N}}$
and an A-definable finite set
$m\in {\mathbb {N}}$
and an A-definable finite set
 $Y\subset K$
which m-s-prepares X.
$Y\subset K$
which m-s-prepares X.
In the sequel, when appealing directly to the definition, we will only need the case
![]() $s=1$
(so
$s=1$
(so
![]() $A'$
does not appear). The parameter s does appear implicitly, though, when applying properties of
$A'$
does not appear). The parameter s does appear implicitly, though, when applying properties of
![]() $1$
-h-minimality such as generic continuity of definable functions (see [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.1.1]).
$1$
-h-minimality such as generic continuity of definable functions (see [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.1.1]).
Below we will need to study properties of ‘one-to-finite definable functions’ (definable correspondences, in the terminology of [Reference Simon and Walsberg15]). It turns out that statements regarding such objects can sometimes be reduced to statements on definable functions in expansions of the language by algebraic Skolem functions (i.e., Skolem functions for definable finite sets). For this, the following will be convenient (see [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 4.3.3] and [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Proposition 3.2.2]):
Fact 2.5. Suppose K is a 1-h-minimal valued field. Then there exists a language
![]() $\mathcal {L}'\supseteq \mathcal {L}$
, an elementary extension
$\mathcal {L}'\supseteq \mathcal {L}$
, an elementary extension
![]() $K'$
of K and an
$K'$
of K and an
![]() $\aleph _0$
-saturated
$\aleph _0$
-saturated
![]() $\mathcal {L}'$
-structure on
$\mathcal {L}'$
-structure on
![]() $K'$
extending the
$K'$
extending the
![]() $\mathcal {L}$
-structure of
$\mathcal {L}$
-structure of
![]() $K'$
, such that
$K'$
, such that
![]() $K'$
is 1-h-minimal as an
$K'$
is 1-h-minimal as an
![]() $\mathcal {L}'$
-structure, and such that
$\mathcal {L}'$
-structure, and such that
![]() $\operatorname {\mathrm {acl}}_{\mathcal {L}'}(A)=\operatorname {\mathrm {dcl}}_{\mathcal {L}'}(A)$
for all
$\operatorname {\mathrm {acl}}_{\mathcal {L}'}(A)=\operatorname {\mathrm {dcl}}_{\mathcal {L}'}(A)$
for all
![]() $A\subseteq K'$
.
$A\subseteq K'$
.
Above and throughout, algebraic and definable closures are always assumed to be taken in the K sort. In the sequel, we will refer to the property appearing in the conclusion of Fact 2.5 simply as ‘
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
’.
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
’.
Remark 2.6. Given an
![]() ${\mathcal L}$
-definable set S, statements concerning topological or geometric properties of S are often expressible by first-order
${\mathcal L}$
-definable set S, statements concerning topological or geometric properties of S are often expressible by first-order
![]() ${\mathcal L}$
-formulas. As the topology on K is definable in the valued field language, and the dimension of definable sets in 1-h-minimal structures is determined by the topology (see Proposition 2.11), the truth values of the hypothesis and conclusion of such statements (for our fixed
${\mathcal L}$
-formulas. As the topology on K is definable in the valued field language, and the dimension of definable sets in 1-h-minimal structures is determined by the topology (see Proposition 2.11), the truth values of the hypothesis and conclusion of such statements (for our fixed
![]() ${\mathcal L}$
-definable set S) are the same in K and in any elementary extension
${\mathcal L}$
-definable set S) are the same in K and in any elementary extension
![]() $K\prec K'$
, as well as in any
$K\prec K'$
, as well as in any
![]() $1$
-h-minimal expansion of the latter. Therefore, by Fact 2.5, in the proof of such statements (for a fixed definable S), there is no harm assuming
$1$
-h-minimal expansion of the latter. Therefore, by Fact 2.5, in the proof of such statements (for a fixed definable S), there is no harm assuming
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
.
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
.
2.1. Geometric structures
We collect a few basic facts about geometric structures. Starting with Proposition 2.11, we apply them to the context of 1-h-mininal fields. Occasionally, we may state the hypothesis in the context of geometric or pregeometric structures when the proof is not simpler in the 1-h-minimal context, but the main application in this paper will always be to 1-h-minimal structures. Geometric structures were introduced in [Reference Hrushovski and Pillay8, §2]. Let us recall the definition: An
![]() $\aleph _0$
-saturated structure, M is pregeometric if
$\aleph _0$
-saturated structure, M is pregeometric if
![]() $\operatorname {\mathrm {acl}}(\cdot )$
is a matroid; that is, it satisfies the exchange property:
$\operatorname {\mathrm {acl}}(\cdot )$
is a matroid; that is, it satisfies the exchange property:
In this situation, the matroid gives a notion of dimension,
![]() $\dim (a/b)$
, the dimension of a tuple a over a tuple b, as the smallest length of a sub-tuple
$\dim (a/b)$
, the dimension of a tuple a over a tuple b, as the smallest length of a sub-tuple
![]() $a'$
of a such that
$a'$
of a such that
![]() $a\in \operatorname {\mathrm {acl}}(a'b)$
, and the dimension of a b-definable set X as the maximum of the dimensions
$a\in \operatorname {\mathrm {acl}}(a'b)$
, and the dimension of a b-definable set X as the maximum of the dimensions
![]() $\dim (a/b)$
with
$\dim (a/b)$
with
![]() $a\in X$
(this does not depend on b). As is customary, we set
$a\in X$
(this does not depend on b). As is customary, we set
![]() $\dim (\emptyset )=-\infty $
. We recall the basic properties of dimension (see [Reference Hrushovski and Pillay8, §2] for all references). This dimension satisfies the additivity property
$\dim (\emptyset )=-\infty $
. We recall the basic properties of dimension (see [Reference Hrushovski and Pillay8, §2] for all references). This dimension satisfies the additivity property
that we will invoke without further reference. We call a and b algebraically independent over c if
![]() $\dim (a/bc)=\dim (a/c)$
. Note that by additivity of dimension, this is a symmetric relation. Note also that additivity implies that if
$\dim (a/bc)=\dim (a/c)$
. Note that by additivity of dimension, this is a symmetric relation. Note also that additivity implies that if
![]() $b,c$
are inter-algebraic over a, meaning
$b,c$
are inter-algebraic over a, meaning
![]() $b\in \operatorname {\mathrm {acl}}(ac)$
and
$b\in \operatorname {\mathrm {acl}}(ac)$
and
![]() $c\in \operatorname {\mathrm {acl}}(ab)$
, then
$c\in \operatorname {\mathrm {acl}}(ab)$
, then
![]() $\dim (b/a)=\dim (c/a)$
(in particular, this holds when c is the image of b under an a-definable bijection). If M is a pregeometric structure and
$\dim (b/a)=\dim (c/a)$
(in particular, this holds when c is the image of b under an a-definable bijection). If M is a pregeometric structure and
![]() $f:X\to Y$
is a surjective definable function with fibers of constant dimension k, then
$f:X\to Y$
is a surjective definable function with fibers of constant dimension k, then
![]() $\dim (X)=\dim (Y)+k$
. This is a consequence of the additivity formula.
$\dim (X)=\dim (Y)+k$
. This is a consequence of the additivity formula.
Given an a-definable set X, a generic element of X over a is an element
![]() $b\in X$
such that
$b\in X$
such that
![]() $\dim (b/a)=\dim (X)$
. Generic elements can always be found in the model by using
$\dim (b/a)=\dim (X)$
. Generic elements can always be found in the model by using
![]() $\aleph _0$
-saturation. We call
$\aleph _0$
-saturation. We call
![]() $Y\subset X$
large if
$Y\subset X$
large if
![]() $\dim (X\setminus Y)<\dim (X)$
. This is equivalent to Y containing every generic point of X.
$\dim (X\setminus Y)<\dim (X)$
. This is equivalent to Y containing every generic point of X.
A pregeometric structure M is called geometric if it eliminates the quantifier
![]() $\exists ^\infty $
. If M is geometric, then dimension is definable in definable families. Namely, for
$\exists ^\infty $
. If M is geometric, then dimension is definable in definable families. Namely, for
![]() $\{X_a\}_{a\in S}$
, a definable family, the set
$\{X_a\}_{a\in S}$
, a definable family, the set
![]() $\{a\in S: \dim (X_a)=k\}$
is definable.
$\{a\in S: \dim (X_a)=k\}$
is definable.
The following simple fact is a translation of the definition of a pregeometry to a property of definable sets. Note as an aside that this reformulation implies that the property of being a pregeometry is preserved under reducts. That is, if M is an
![]() $\aleph _0$
-saturated pregeometric
$\aleph _0$
-saturated pregeometric
![]() $\mathcal {L}'$
-structure, and
$\mathcal {L}'$
-structure, and
![]() $\mathcal {L}\subset \mathcal {L}'$
, then M is also a pregeometric
$\mathcal {L}\subset \mathcal {L}'$
, then M is also a pregeometric
![]() $\mathcal {L}$
-structure. For the sake of completeness, we give the proof:
$\mathcal {L}$
-structure. For the sake of completeness, we give the proof:
Fact 2.7. Suppose M is an
![]() $\aleph _0$
-saturated structure. Then M is pregeometric if and only if for every definable
$\aleph _0$
-saturated structure. Then M is pregeometric if and only if for every definable
![]() $X\subset M\times M$
, if the projection,
$X\subset M\times M$
, if the projection,
![]() $\pi _1:X\to M$
, into the first factor is finite-to-one, then the set
$\pi _1:X\to M$
, into the first factor is finite-to-one, then the set
![]() $Y=\{c\in M: \pi _2^{-1}(c)\cap X\text { is infinite}\}$
is finite, where
$Y=\{c\in M: \pi _2^{-1}(c)\cap X\text { is infinite}\}$
is finite, where
![]() $\pi _2$
is the projection into the second factor.
$\pi _2$
is the projection into the second factor.
Proof. Suppose M is pregeometric and suppose
![]() $X\subset M\times M$
is A-definable such that
$X\subset M\times M$
is A-definable such that
![]() $\pi _1^{-1}(x)\cap X$
is finite for all
$\pi _1^{-1}(x)\cap X$
is finite for all
![]() $x\in M$
. Suppose also that
$x\in M$
. Suppose also that
![]() $Y=\{y\in M: \pi _2^{-1}(y)\cap X\text { is infinite}\}$
is infinite. By compactness and saturation, we can choose
$Y=\{y\in M: \pi _2^{-1}(y)\cap X\text { is infinite}\}$
is infinite. By compactness and saturation, we can choose
![]() $b\in Y$
such that
$b\in Y$
such that
![]() ${\dim (b/A)=1}$
. Similarly, we can find
${\dim (b/A)=1}$
. Similarly, we can find
![]() $a\in \pi _2^{-1}(b)\cap X$
such that
$a\in \pi _2^{-1}(b)\cap X$
such that
![]() $\dim (a/Ab)=1$
. We conclude that
$\dim (a/Ab)=1$
. We conclude that
![]() $\dim (ab/A)=2$
, and so
$\dim (ab/A)=2$
, and so
![]() $\dim (X)\ge 2$
. This contradicts the fact that
$\dim (X)\ge 2$
. This contradicts the fact that
![]() $\pi _1^{-1}(x)\cap X$
is finite for all
$\pi _1^{-1}(x)\cap X$
is finite for all
![]() $x\in M$
.
$x\in M$
.
For the converse, suppose A is a finite subset of M and
![]() $a,b\in M$
are singletons such that
$a,b\in M$
are singletons such that
![]() $a\in \operatorname {\mathrm {acl}}(Ab)\setminus \operatorname {\mathrm {acl}}(A)$
. Then there is an A-definable set
$a\in \operatorname {\mathrm {acl}}(Ab)\setminus \operatorname {\mathrm {acl}}(A)$
. Then there is an A-definable set
![]() $X\subset M\times M$
such that
$X\subset M\times M$
such that
![]() $(b,a)\in X$
and
$(b,a)\in X$
and
![]() $\pi _1^{-1}(b)\cap X$
is finite, say of cardinality k. If we take
$\pi _1^{-1}(b)\cap X$
is finite, say of cardinality k. If we take
![]() $Z=\{c\in M: \pi _1^{-1}(c)\cap X\text { has cardinality }k\}$
, then we may replace X by
$Z=\{c\in M: \pi _1^{-1}(c)\cap X\text { has cardinality }k\}$
, then we may replace X by
![]() $X\cap Z\times M$
, and we may assume that
$X\cap Z\times M$
, and we may assume that
![]() $\pi _1^{-1}(c)\cap X$
is either empty or of constant finite cardinality for all
$\pi _1^{-1}(c)\cap X$
is either empty or of constant finite cardinality for all
![]() $c\in M$
. In this case, by the hypothesis, we conclude that
$c\in M$
. In this case, by the hypothesis, we conclude that
![]() $Y=\{y\in M: \pi _2^{-1}(y)\cap M\text { is infinite}\}$
is finite. Note that Y is A-invariant and definable, so it is A-definable. We conclude that
$Y=\{y\in M: \pi _2^{-1}(y)\cap M\text { is infinite}\}$
is finite. Note that Y is A-invariant and definable, so it is A-definable. We conclude that
![]() $a\notin Y$
because
$a\notin Y$
because
![]() $a\notin \operatorname {\mathrm {acl}}(A)$
, and so
$a\notin \operatorname {\mathrm {acl}}(A)$
, and so
![]() $b\in \operatorname {\mathrm {acl}}(Aa)$
as required.
$b\in \operatorname {\mathrm {acl}}(Aa)$
as required.
The next characterisation of the
![]() $\operatorname {\mathrm {acl}}$
-dimension should be well known:
$\operatorname {\mathrm {acl}}$
-dimension should be well known:
Fact 2.8. Suppose M is an
![]() $\aleph _0$
-saturated structure, which eliminates the
$\aleph _0$
-saturated structure, which eliminates the
![]() $\exists ^{\infty }$
quantifier. Suppose there is a function,
$\exists ^{\infty }$
quantifier. Suppose there is a function,
![]() $X\mapsto d(X)$
, from the nonempty definable subsets of (cartesian powers of) M into
$X\mapsto d(X)$
, from the nonempty definable subsets of (cartesian powers of) M into
![]() $\mathbb {N}$
satisfying the following:
$\mathbb {N}$
satisfying the following:
-
(1) If
 $X\subset M^n\times M$
is such that the first coordinate projection
$X\subset M^n\times M$
is such that the first coordinate projection
 $\pi _1:X\to M^n$
is finite to one, then
$\pi _1:X\to M^n$
is finite to one, then
 $d(X)=d(\pi _1(X))$
.
$d(X)=d(\pi _1(X))$
. -
(2) If
 $X\subset M^n\times M$
and
$X\subset M^n\times M$
and
 $\pi _1:X\to M^n$
is a projection, all of whose fibres are either empty or infinite, then
$\pi _1:X\to M^n$
is a projection, all of whose fibres are either empty or infinite, then
 $d(X)=d(\pi _1(X))+1$
.
$d(X)=d(\pi _1(X))+1$
. -
(3) If
 $\pi :M^n\to M^n$
is a coordinate permutation, then
$\pi :M^n\to M^n$
is a coordinate permutation, then
 $d(X)=d(\pi (X))$
.
$d(X)=d(\pi (X))$
. -
(4)
 $d(X\cup Y)=\max \{d(X),d(Y)\}$
.
$d(X\cup Y)=\max \{d(X),d(Y)\}$
. -
(5)
 $d(M)=1$
$d(M)=1$
-
(6)
 $d(X)=0$
if and only if X is finite.
$d(X)=0$
if and only if X is finite.
Then M is a geometric structure and d coincides with its
![]() ${\mathit {acl}}$
-dimension.
${\mathit {acl}}$
-dimension.
Proof. It suffices to show that M is pregeometric. We use Fact 2.7. Let
![]() $X\subset M\times M$
be such that
$X\subset M\times M$
be such that
![]() $\pi _1^{-1}(x)\cap X$
is finite for all
$\pi _1^{-1}(x)\cap X$
is finite for all
![]() $x\in M$
. Take
$x\in M$
. Take
![]() $Y=\{y\in M: \pi _2^{-1}(y)\cap X\text { is infinite}\}$
. Because M eliminates the
$Y=\{y\in M: \pi _2^{-1}(y)\cap X\text { is infinite}\}$
. Because M eliminates the
![]() $\exists ^{\infty }$
quantifier, we have that Y is definable. If Y is infinite, we conclude that
$\exists ^{\infty }$
quantifier, we have that Y is definable. If Y is infinite, we conclude that
![]() $d(X)\ge d(X\cap \pi _2^{-1}(Y))=d(Y)+1=2$
, the first inequality by item (4), the second equality by items (3) and (2), and the third by item (6). However,
$d(X)\ge d(X\cap \pi _2^{-1}(Y))=d(Y)+1=2$
, the first inequality by item (4), the second equality by items (3) and (2), and the third by item (6). However,
![]() $d(X)=d(\pi _1(X))\le d(M)=1$
, the first equality by item (1), the second inequality by item (4) and the third by item (5). This is a contradiction and finishes the proof.
$d(X)=d(\pi _1(X))\le d(M)=1$
, the first equality by item (1), the second inequality by item (4) and the third by item (5). This is a contradiction and finishes the proof.
To see that
![]() $d(X)=\dim (X)$
for
$d(X)=\dim (X)$
for
![]() $X\subset M^n$
, we may proceed by induction on n. The base case
$X\subset M^n$
, we may proceed by induction on n. The base case
![]() $n=1$
follows from item (4), (5) and (6). So suppose that
$n=1$
follows from item (4), (5) and (6). So suppose that
![]() $X\subset M^n\times M$
. Denote
$X\subset M^n\times M$
. Denote
![]() $Y=\{x\in M^n: \pi _1^{-1}(x)\cap X\text { is infinite}\}$
. By hypothesis, Y is a definable set. Denote
$Y=\{x\in M^n: \pi _1^{-1}(x)\cap X\text { is infinite}\}$
. By hypothesis, Y is a definable set. Denote
![]() $X_1=\pi _1^{-1}(Y)\cap X$
and
$X_1=\pi _1^{-1}(Y)\cap X$
and
![]() $X_2=X\setminus X_1$
. Then by items (1), (2) and (4), we conclude that
$X_2=X\setminus X_1$
. Then by items (1), (2) and (4), we conclude that
![]() $d(X)=\max \{d(X_1),d(X_2)\}=\max \{d(Y)+1,d(\pi _1(X)\setminus Y)\}$
. For the same reason, we have the formula
$d(X)=\max \{d(X_1),d(X_2)\}=\max \{d(Y)+1,d(\pi _1(X)\setminus Y)\}$
. For the same reason, we have the formula
![]() $\dim (X)=\max \{\dim (Y)+1,\dim (\pi _1(X)\setminus Y)\}$
, so
$\dim (X)=\max \{\dim (Y)+1,\dim (\pi _1(X)\setminus Y)\}$
, so
![]() $d(X)=\dim (X)$
, as required.
$d(X)=\dim (X)$
, as required.
The next fact is also standard:
Fact 2.9. Suppose M is a geometric structure. Suppose
![]() $X\subset M^n$
is a-definable. Then there is a partition of X into a finite number of a-definable sets
$X\subset M^n$
is a-definable. Then there is a partition of X into a finite number of a-definable sets
![]() $X=X_1\cup \cdots \cup X_n$
, such that for each member of the partition
$X=X_1\cup \cdots \cup X_n$
, such that for each member of the partition
![]() $X_k$
, there is a coordinate projection
$X_k$
, there is a coordinate projection
![]() $\pi :X_k\to M^r$
which is finite to one and has image of dimension r.
$\pi :X_k\to M^r$
which is finite to one and has image of dimension r.
Remark 2.10. For this statement, we need to allow the identity
![]() $\mathrm {id}:M^n\to M^n$
as well as the constant function
$\mathrm {id}:M^n\to M^n$
as well as the constant function
![]() $M^n\to M^{0}$
as coordinate projections. For the above, recall that
$M^n\to M^{0}$
as coordinate projections. For the above, recall that
![]() $M^{0}$
is a set consisting of one element.
$M^{0}$
is a set consisting of one element.
Proof. By induction on the dimension of the ambient space n. Consider the projection onto the first
![]() $n-1$
coordinates
$n-1$
coordinates
![]() $\pi _1:M^n\to M^{n-1}$
. Then the set
$\pi _1:M^n\to M^{n-1}$
. Then the set
![]() $Y\subset M^{n-1}$
of y such that the fibers
$Y\subset M^{n-1}$
of y such that the fibers
![]() $X_y=\pi _1^{-1}(y)\cap X$
are infinite is definable. So partitioning X, we may assume all the nonempty fibers of X over
$X_y=\pi _1^{-1}(y)\cap X$
are infinite is definable. So partitioning X, we may assume all the nonempty fibers of X over
![]() $M^{n-1}$
are finite, or all are infinite. If all the fibers of
$M^{n-1}$
are finite, or all are infinite. If all the fibers of
![]() $X\to K^{n-1}$
are finite then we finish by induction.
$X\to K^{n-1}$
are finite then we finish by induction.
If all the nonempty fibers are infinite, then by the induction, there is a partition
![]() $Y=\bigcup _i Y_i$
, and for each
$Y=\bigcup _i Y_i$
, and for each
![]() $Y_i$
, there is a coordinate projection
$Y_i$
, there is a coordinate projection
![]() $\tau : Y_i\to K^r$
with finite fibers and
$\tau : Y_i\to K^r$
with finite fibers and
![]() $r=\dim (Y_i)$
. Denote
$r=\dim (Y_i)$
. Denote
![]() $\pi _2:M^{n}\to M$
the projection onto the last coordinate. Then setting
$\pi _2:M^{n}\to M$
the projection onto the last coordinate. Then setting
![]() $X_i=X\cap \pi _1^{-1}(Y_i)$
, the projection
$X_i=X\cap \pi _1^{-1}(Y_i)$
, the projection
![]() $\pi (x)=(\tau (\pi _1(x)),\pi _2(x))$
has the desired properties.
$\pi (x)=(\tau (\pi _1(x)),\pi _2(x))$
has the desired properties.
The next proposition is key. It asserts that
![]() $1$
-h-minimal fields are geometric, and it connects (combined with the previous fact) topology and dimension in such structures:
$1$
-h-minimal fields are geometric, and it connects (combined with the previous fact) topology and dimension in such structures:
Proposition 2.11. Suppose K is a 1-h-minimal valued field. Then
-
(1) K is a geometric structure.
-
(2) Every definable
 $X\subset K^n$
satisfies
$X\subset K^n$
satisfies
 $\dim (X)=n$
if and only if X has nonempty interior, and
$\dim (X)=n$
if and only if X has nonempty interior, and
 $\dim (X)<n$
if and only if X is nowhere dense.
$\dim (X)<n$
if and only if X is nowhere dense. -
(3) For a definable
 $X\subset K^n$
, we have
$X\subset K^n$
, we have
 $\dim (X)=\max \limits _{x\in X}\dim _x(X)$
, where we denote
$\dim (X)=\max \limits _{x\in X}\dim _x(X)$
, where we denote
 $\dim _x(X)$
, the local dimension of X at x, defined as
$\dim _x(X)$
, the local dimension of X at x, defined as  $$\begin{align*}\dim_x(X)= \min\{\dim(B\cap X): x\in B \text{ is an open ball}\}.\end{align*}$$
$$\begin{align*}\dim_x(X)= \min\{\dim(B\cap X): x\in B \text{ is an open ball}\}.\end{align*}$$
Proof. This is essentially items (1)–(5) of [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.3.4] in residue characteristic
![]() $0$
and contained in [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Proposition 3.1.1] in mixed characteristic.
$0$
and contained in [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Proposition 3.1.1] in mixed characteristic.
For example, assume K has residue characteristic
![]() $0$
. That K is geometric is proved in the course of the proof of [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.3.4]. We can also derive it from Fact 2.8 and [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.3.4].
$0$
. That K is geometric is proved in the course of the proof of [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.3.4]. We can also derive it from Fact 2.8 and [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.3.4].
The topological characterisation asserting that
![]() $\dim (X)=n$
if and only if X has nonempty interior is a particular case of item (1) in [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.3.4]. That
$\dim (X)=n$
if and only if X has nonempty interior is a particular case of item (1) in [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.3.4]. That
![]() $\dim (X)<n$
if and only if X is nowhere dense follows from this. Indeed, if
$\dim (X)<n$
if and only if X is nowhere dense follows from this. Indeed, if
![]() $\dim (X)=n$
, then X has nonempty interior and so it is somewhere dense. If
$\dim (X)=n$
, then X has nonempty interior and so it is somewhere dense. If
![]() $\dim (X)<n$
and
$\dim (X)<n$
and
![]() $U\subset K^n$
is nonempty open, then
$U\subset K^n$
is nonempty open, then
![]() $\dim (U\setminus X)=n$
, and so
$\dim (U\setminus X)=n$
, and so
![]() $U\setminus X$
has nonempty interior. This implies X is nowhere dense.
$U\setminus X$
has nonempty interior. This implies X is nowhere dense.
That dimension is the maximum of the local dimensions is item (5) of Proposition 5.3.4 of [Reference Cluckers, Halupczok and Rideau-Kikuchi4]
Proposition 2.12. Suppose K is a 1-h-minimal field. Suppose
![]() $f:U\to K^m$
is a definable function. Then there is a definable open dense subset
$f:U\to K^m$
is a definable function. Then there is a definable open dense subset
![]() $U'\subset U$
such that
$U'\subset U$
such that
![]() $f:U'\to K^m$
is continuous.
$f:U'\to K^m$
is continuous.
Proof. This is essentially a particular case of [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.1.1] in residue characteristic
![]() $0$
and contained in [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Proposition 3.1.1] in mixed characteristic.
$0$
and contained in [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Proposition 3.1.1] in mixed characteristic.
Indeed, because the intersection of open dense sets is open and dense, we reduce to the case
![]() $m=1$
. From those propositions, one gets that the set Z of points where f is continuous is dense in U. As Z is somewhere dense, we conclude using item (2) of Proposition 2.11 that
$m=1$
. From those propositions, one gets that the set Z of points where f is continuous is dense in U. As Z is somewhere dense, we conclude using item (2) of Proposition 2.11 that
![]() $\dim (Z)=n$
and so Z has nonempty interior. If
$\dim (Z)=n$
and so Z has nonempty interior. If
![]() $V\subset U$
is a nonempty open definable subset, then, as
$V\subset U$
is a nonempty open definable subset, then, as
![]() $Z\cap V$
is the set of points at which
$Z\cap V$
is the set of points at which
![]() $f|_{V}$
is continuous, by what we just proved,
$f|_{V}$
is continuous, by what we just proved,
![]() $Z\cap V$
has nonempty interior. We conclude that the set of points at which f is continuous has a dense interior in U, as desired.
$Z\cap V$
has nonempty interior. We conclude that the set of points at which f is continuous has a dense interior in U, as desired.
Next, we describe a topology for
![]() $Y^{[s]}$
, the set of subsets of Y of cardinality s, for Y a Hausdorff topological space, and s a positive integer. We prove a slightly more general statement that will be applied when X is
$Y^{[s]}$
, the set of subsets of Y of cardinality s, for Y a Hausdorff topological space, and s a positive integer. We prove a slightly more general statement that will be applied when X is
![]() $Y^s\setminus \Delta $
, the set of tuples of
$Y^s\setminus \Delta $
, the set of tuples of
![]() $Y^s$
with distinct coordinates and the symmetric group,
$Y^s$
with distinct coordinates and the symmetric group,
![]() $S_s$
, on s elements acting on
$S_s$
, on s elements acting on
![]() $Y^s$
by coordinate permutation, in which case the orbit space is identified with
$Y^s$
by coordinate permutation, in which case the orbit space is identified with
![]() $Y^{[s]}$
.
$Y^{[s]}$
.
Fact 2.13. Suppose X is a Hausdorff topological space and G is a finite group acting on X by homeomorphisms, such that every
![]() $x\in X$
has a trivial stabiliser in G. Then
$x\in X$
has a trivial stabiliser in G. Then
![]() $X/G$
equipped with the quotient topology is Hausdorff and the map
$X/G$
equipped with the quotient topology is Hausdorff and the map
![]() $p:X\to X/G$
is a closed finite covering map. In fact, for every
$p:X\to X/G$
is a closed finite covering map. In fact, for every
![]() $x\in X$
, there is an open set
$x\in X$
, there is an open set
![]() $x\in U\subset X$
such that
$x\in U\subset X$
such that
![]() $\{gU: g\in G\}$
are pairwise disjoint,
$\{gU: g\in G\}$
are pairwise disjoint,
![]() $p^{-1}p(U)=\bigcup _ggU$
and
$p^{-1}p(U)=\bigcup _ggU$
and
![]() $p|_{gU}$
is a homeomorphism onto
$p|_{gU}$
is a homeomorphism onto
![]() $p(U)$
.
$p(U)$
.
Proof. We know that p is open since
![]() $p^{-1}p(U)=\bigcup _{g\in G}gU$
is open for U open. Consider the orbit
$p^{-1}p(U)=\bigcup _{g\in G}gU$
is open for U open. Consider the orbit
![]() $\{gx\}_{g\in G}$
of x. By assumption, if
$\{gx\}_{g\in G}$
of x. By assumption, if
![]() $g\neq h$
, then
$g\neq h$
, then
![]() $gx\neq hx$
. Let V be an open set in X containing
$gx\neq hx$
. Let V be an open set in X containing
![]() $\{gx\}_{g\in G}$
. Now, because X is Hausdorff, there are
$\{gx\}_{g\in G}$
. Now, because X is Hausdorff, there are
![]() $U_g$
open neighborhoods of
$U_g$
open neighborhoods of
![]() $gx$
, contained in V, such that
$gx$
, contained in V, such that
![]() $U_g\cap U_h=\emptyset $
for
$U_g\cap U_h=\emptyset $
for
![]() $g\neq h$
. If we take
$g\neq h$
. If we take
![]() $U=\bigcap _{g\in G}g^{-1}U_g$
, then
$U=\bigcap _{g\in G}g^{-1}U_g$
, then
![]() $gU\subset U_g$
and so
$gU\subset U_g$
and so
![]() $\{gU: g\in G\}$
are pairwise disjoint. We conclude that p is closed and restricted to
$\{gU: g\in G\}$
are pairwise disjoint. We conclude that p is closed and restricted to
![]() $gU$
is a homeomorphism. That
$gU$
is a homeomorphism. That
![]() $X/G$
is Hausdorff now follows from this. Indeed, if
$X/G$
is Hausdorff now follows from this. Indeed, if
![]() $p(x)\neq p(y)$
, then there are open sets
$p(x)\neq p(y)$
, then there are open sets
![]() $V_1$
and
$V_1$
and
![]() $V_2$
of X, which are disjoint and such that
$V_2$
of X, which are disjoint and such that
![]() $p^{-1}p(x)\subset V_1$
and
$p^{-1}p(x)\subset V_1$
and
![]() $p^{-1}p(y)\subset V_2$
. Because p is closed, there are open sets
$p^{-1}p(y)\subset V_2$
. Because p is closed, there are open sets
![]() $p(x)\in U_1$
and
$p(x)\in U_1$
and
![]() $p(y)\in U_2$
in
$p(y)\in U_2$
in
![]() $X/G$
such that
$X/G$
such that
![]() $p^{-1}(U_i)\subset V_i$
. We conclude that
$p^{-1}(U_i)\subset V_i$
. We conclude that
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are disjoint.
$U_2$
are disjoint.
With respect to this topology, we get the following:
Proposition 2.14. Let K be a 1-h-minimal valued field. Suppose
![]() $U\subset K^n$
is open and
$U\subset K^n$
is open and
![]() $f:U\to (K^r)^{[s]}$
is definable. Then there is an open dense definable set
$f:U\to (K^r)^{[s]}$
is definable. Then there is an open dense definable set
![]() $U'\subset U$
such that f is continuous in
$U'\subset U$
such that f is continuous in
![]() $U'$
.
$U'$
.
Proof. This statement is equivalent to saying that the interior of the set of points on which f is continuous is dense. As this property is expressible by a first order formula, we may assume
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
; see Fact 2.5 and the remark following it.
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
; see Fact 2.5 and the remark following it.
In that case, we have a definable section
![]() $\sigma :(K^r)^{[s]}\to K^{rs}$
, and if
$\sigma :(K^r)^{[s]}\to K^{rs}$
, and if
![]() $V\subseteq U$
is open dense such that
$V\subseteq U$
is open dense such that
![]() $\sigma f$
is continuous, as provided by Proposition 2.12, then f is continuous in V.
$\sigma f$
is continuous, as provided by Proposition 2.12, then f is continuous in V.
Proposition 2.15. Suppose
![]() $X\subset K^n$
is b-definable. Then there is finite partition of X into b-definable sets, such that for each element Y of the partition, there is a coordinate projection
$X\subset K^n$
is b-definable. Then there is finite partition of X into b-definable sets, such that for each element Y of the partition, there is a coordinate projection
![]() $\pi :Y\to U$
onto an open set
$\pi :Y\to U$
onto an open set
![]() $U\subset K^m$
, such that the fibers of
$U\subset K^m$
, such that the fibers of
![]() $\pi $
all have the same cardinality equal to s, and the associated map
$\pi $
all have the same cardinality equal to s, and the associated map
![]() $f:U\to (K^{n-m})^{[s]}$
is continuous.
$f:U\to (K^{n-m})^{[s]}$
is continuous.
Remark 2.16. As in Remark 2.10, we need to allow the two cases
![]() $m=0$
and
$m=0$
and
![]() $m=n$
. The set
$m=n$
. The set
![]() $K^0$
consists of a single point and has a unique topology.
$K^0$
consists of a single point and has a unique topology.
Proof. This is a consequence of dimension theory and the previous observation. In more detail, we proceed by induction on the dimension of X.
First, recall that X has a finite partition into b-definable sets such that for each set
![]() $X'$
in the partition, there is a coordinate projection
$X'$
in the partition, there is a coordinate projection
![]() $\pi :X'\to K^r$
with finite fibers and
$\pi :X'\to K^r$
with finite fibers and
![]() $r=\dim (X')$
; see Fact 2.9.
$r=\dim (X')$
; see Fact 2.9.
So now assume
![]() $\pi :X\to K^r$
is a coordinate projection with finite fibers and
$\pi :X\to K^r$
is a coordinate projection with finite fibers and
![]() $r=\dim (X)$
, and denote
$r=\dim (X)$
, and denote
![]() $\pi ':X\to K^{n-r}$
the projection into the other coordinates. There is an integer s which bounds the cardinality of the fibers of
$\pi ':X\to K^{n-r}$
the projection into the other coordinates. There is an integer s which bounds the cardinality of the fibers of
![]() $\pi $
. If we denote
$\pi $
. If we denote
![]() $Y_k$
the set of elements
$Y_k$
the set of elements
![]() $a\in K^r$
such that
$a\in K^r$
such that
![]() $X_a=\pi '(\pi ^{-1}(a))$
has cardinality k, then we get
$X_a=\pi '(\pi ^{-1}(a))$
has cardinality k, then we get
![]() $Y_0\cup \cdots \cup Y_s=K^r$
. Now let
$Y_0\cup \cdots \cup Y_s=K^r$
. Now let
![]() $V_j\subset Y_j$
be open dense in the interior of
$V_j\subset Y_j$
be open dense in the interior of
![]() $Y_j$
and such that the map
$Y_j$
and such that the map
![]() $V_j\to (K^{n-r})^{[j]}$
given by
$V_j\to (K^{n-r})^{[j]}$
given by
![]() $a\mapsto X_a$
is continuous; see Proposition 2.14. Then the set
$a\mapsto X_a$
is continuous; see Proposition 2.14. Then the set
![]() $\{x\in X: \pi (x)\in Y_j\setminus V_j, 1\leq j\leq s\}$
is of lower dimension than X, by item 2 of Proposition 2.11, and so we may apply the induction hypothesis on it.
$\{x\in X: \pi (x)\in Y_j\setminus V_j, 1\leq j\leq s\}$
is of lower dimension than X, by item 2 of Proposition 2.11, and so we may apply the induction hypothesis on it.
Recall that a subset
![]() $Y\subset X$
of a topological space X is locally closed if it is the intersection of an open set and a closed set. This is equivalent to Y being relatively open in its closure. It is also equivalent to, for every point
$Y\subset X$
of a topological space X is locally closed if it is the intersection of an open set and a closed set. This is equivalent to Y being relatively open in its closure. It is also equivalent to, for every point
![]() $y\in Y$
, the existence of a neighborhood V of y, such that
$y\in Y$
, the existence of a neighborhood V of y, such that
![]() $Y\cap V$
is relatively closed in V.
$Y\cap V$
is relatively closed in V.
Proposition 2.17. Suppose K is 1-h-minimal and
![]() $X\subset K^n$
an a-definable set. Then X is a finite union of a-definable locally closed subsets of
$X\subset K^n$
an a-definable set. Then X is a finite union of a-definable locally closed subsets of
![]() $K^n$
.
$K^n$
.
Proof. This is a consequence of Proposition 2.15. Namely, there is a partition of X into a finite union of a-definable subsets for each of which there is a coordinate projection with finite fibers onto an open set U, so we may assume X is of this form. We may further assume that the fibers have constant cardinality k and the associated mapping
![]() $U\to (K^r)^{[k]}$
is continuous. Then X is closed in
$U\to (K^r)^{[k]}$
is continuous. Then X is closed in
![]() $U\times K^r$
and so locally closed.
$U\times K^r$
and so locally closed.
We finish by reviewing a more difficult property of dimension. We will only use this in Proposition 5.20, Proposition 6.9 and Corollary 6.14, which are not used in the main theorems.
Proposition 2.18. Suppose K is a 1-h-minimal field and
![]() $X\subset K^n$
. Then
$X\subset K^n$
. Then
![]() $\dim (\operatorname {\mathrm {cl}}(X)\setminus X)<\dim (X)$
.
$\dim (\operatorname {\mathrm {cl}}(X)\setminus X)<\dim (X)$
.
This is item 6 of [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Proposition 5.3.4] for the residue characteristic
![]() $0$
, and it is contained in Proposition 3.1.1 of [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5] in the mixed characteristic case.
$0$
, and it is contained in Proposition 3.1.1 of [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5] in the mixed characteristic case.
3. Taylor approximations
In this section, we show that, in the
![]() $1$
-h-minimal setting, the generic one variable Taylor approximation theorem ([Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Theorem 3.1.2]) implies a multi-variable version of the theorem. In equi-characteristic
$1$
-h-minimal setting, the generic one variable Taylor approximation theorem ([Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Theorem 3.1.2]) implies a multi-variable version of the theorem. In equi-characteristic
![]() $0$
, this is [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Theorem 5.6.1]. Although the proof in mixed characteristic is essentially similar, we give the details for the sake of completeness and in view of the importance of this result in the sequel.
$0$
, this is [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Theorem 5.6.1]. Although the proof in mixed characteristic is essentially similar, we give the details for the sake of completeness and in view of the importance of this result in the sequel.
We then proceed to introducing some regularity conditions for definable functions (implied in the present context by Taylor’s approximation theorem) necessary for computations related to the Lie algebra of definable groups.
First, we recall the multi-index notation. If
![]() $i=(i_1,\dots ,i_n)\in \mathbb {N}^n$
, we denote
$i=(i_1,\dots ,i_n)\in \mathbb {N}^n$
, we denote
![]() $|i|=i_1+\cdots +i_n$
and
$|i|=i_1+\cdots +i_n$
and
![]() $i!=i_1!\cdots i_n!$
. For
$i!=i_1!\cdots i_n!$
. For
![]() $x=(x_1,\cdots ,x_n)\in K^n$
, we denote
$x=(x_1,\cdots ,x_n)\in K^n$
, we denote
![]() $x^i=x_1^{i_1}\cdots x_n^{i_n}$
. Also, if
$x^i=x_1^{i_1}\cdots x_n^{i_n}$
. Also, if
![]() $f:U\to K$
is a function defined in an open set of
$f:U\to K$
is a function defined in an open set of
![]() $K^n$
, we denote
$K^n$
, we denote
![]() $f^{(i)}(x)=(\frac {\partial ^{i_1}}{\partial x_1^{i_1}} \cdots \frac {\partial ^{i_n}}{\partial x_n^{i_n}}f)(x)$
whenever it exists. Note that we are not assuming equality of mixed derivatives, but see Corollary 3.6.
$f^{(i)}(x)=(\frac {\partial ^{i_1}}{\partial x_1^{i_1}} \cdots \frac {\partial ^{i_n}}{\partial x_n^{i_n}}f)(x)$
whenever it exists. Note that we are not assuming equality of mixed derivatives, but see Corollary 3.6.
Proposition 3.1. Let K be a 1-h-minimal field of residue characteristic
![]() $0$
. Suppose
$0$
. Suppose
![]() $f:U\to K$
is an a-definable function with
$f:U\to K$
is an a-definable function with
![]() $U\subset K^n$
open and let
$U\subset K^n$
open and let
![]() $r\in {\mathbb {N}}$
. Then there is an a-definable set C, of dimension strictly smaller than n, such that for any open ball
$r\in {\mathbb {N}}$
. Then there is an a-definable set C, of dimension strictly smaller than n, such that for any open ball
![]() $B\subseteq U$
disjoint from C, the derivative
$B\subseteq U$
disjoint from C, the derivative
![]() $f^{(i)}$
exists in B for every i with
$f^{(i)}$
exists in B for every i with
![]() $|i|\leq r$
and has constant valuation in B. Moreover,
$|i|\leq r$
and has constant valuation in B. Moreover,
 $$ \begin{align*} \left | f(x)-\sum_{\{i:|i|<r\}}\frac{1}{i!}f^{(i)}(x_0)(x-x_0)^i \right | \leq \max_{\{i:|i|=r\}} \left |\frac{1}{i!}f^{(i)}(x_0)(x-x_0)^i \right| \end{align*} $$
$$ \begin{align*} \left | f(x)-\sum_{\{i:|i|<r\}}\frac{1}{i!}f^{(i)}(x_0)(x-x_0)^i \right | \leq \max_{\{i:|i|=r\}} \left |\frac{1}{i!}f^{(i)}(x_0)(x-x_0)^i \right| \end{align*} $$
for every
![]() $x,x_0\in B$
.
$x,x_0\in B$
.
This is [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Theorem 5.6.1]. Our first order of business is to adapt this result to positive residue characteristic.
The following fact is proved by a standard compactness argument and is often applied implicitly. We add this argument for convenience.
Fact 3.2. Let M be an
![]() $\aleph _0$
-saturated structure and
$\aleph _0$
-saturated structure and
![]() $\{\Phi ^l(\bar {D})\}_{l\in I}$
be a family of properties of definable sets
$\{\Phi ^l(\bar {D})\}_{l\in I}$
be a family of properties of definable sets
![]() $\bar {D}=(D_1,\dots ,D_n)$
in M, indexed by a directed set I. Let b be a tuple in M and S a b-definable set. Assume that
$\bar {D}=(D_1,\dots ,D_n)$
in M, indexed by a directed set I. Let b be a tuple in M and S a b-definable set. Assume that
-
(1) For all l, the property
 $\Phi ^l$
is definable in definable families. That is, if for
$\Phi ^l$
is definable in definable families. That is, if for
 $i=1,\dots ,n$
, we have
$i=1,\dots ,n$
, we have
 $\{D_{i,a}\}_{a\in T}$
b-definable families, then the set
$\{D_{i,a}\}_{a\in T}$
b-definable families, then the set
 $\{a\in T: \Phi ^l({\bar {D}_a})\text { holds}\}$
is b-definable.
$\{a\in T: \Phi ^l({\bar {D}_a})\text { holds}\}$
is b-definable. -
(2)
 $\Phi ^l$
implies
$\Phi ^l$
implies
 $\Phi ^{l'}$
for all
$\Phi ^{l'}$
for all
 $l\leq l'$
.
$l\leq l'$
. -
(3) For every
 $a\in S$
, and for
$a\in S$
, and for
 $i=1,\dots ,n$
, there are
$i=1,\dots ,n$
, there are
 $ba$
-definable sets
$ba$
-definable sets
 $D_{i,a}$
, satisfying
$D_{i,a}$
, satisfying
 $\Phi ^{l_a}$
for some
$\Phi ^{l_a}$
for some
 $l_a\in I$
.
$l_a\in I$
.
Then for
![]() $i=1,\dots , n$
, there are
$i=1,\dots , n$
, there are
![]() $\{D_{i,a}\}_{a\in S}$
b-definable families of sets, and a fixed
$\{D_{i,a}\}_{a\in S}$
b-definable families of sets, and a fixed
![]() $l\in I$
, such that
$l\in I$
, such that
![]() $\Phi ^l(\bar {D}_{a})$
holds for every
$\Phi ^l(\bar {D}_{a})$
holds for every
![]() $a\in S$
.
$a\in S$
.
Remark 3.3. Formally,
![]() $\Phi ^l$
is a subset of
$\Phi ^l$
is a subset of
and we say
![]() $\Phi ^l(D_1,\dots ,D_n)$
holds if the tuple
$\Phi ^l(D_1,\dots ,D_n)$
holds if the tuple
![]() $(D_1,\cdots ,D_n)$
belongs to
$(D_1,\cdots ,D_n)$
belongs to
![]() $\Phi ^l$
.
$\Phi ^l$
.
Note also that the tuple
![]() $(D_1,\dots ,D_n)$
can be replaced with
$(D_1,\dots ,D_n)$
can be replaced with
![]() $D_1\times \cdots \times D_n$
, so there is no loss of generality in taking
$D_1\times \cdots \times D_n$
, so there is no loss of generality in taking
![]() $\Phi ^l$
of the form
$\Phi ^l$
of the form
![]() $\Phi ^l(D)$
.
$\Phi ^l(D)$
.
Proof. Note that by the previous remark, it suffices to prove the result for
![]() $n=1$
, as we shall presently proceed to do. Let
$n=1$
, as we shall presently proceed to do. Let
![]() $a\in S$
. By hypothesis, there is a b-definable family
$a\in S$
. By hypothesis, there is a b-definable family
![]() $\{D_{a'}^a\}_{a'\in S^{0,a}}$
and an element
$\{D_{a'}^a\}_{a'\in S^{0,a}}$
and an element
![]() $l^a\in I$
, such that
$l^a\in I$
, such that
![]() $D_{a}^a$
satisfies
$D_{a}^a$
satisfies
![]() $\Phi ^{l^a}$
. Consider
$\Phi ^{l^a}$
. Consider
![]() $S^a$
to be the set of
$S^a$
to be the set of
![]() $a'\in S$
such that
$a'\in S$
such that
![]() $a'\in S^{0,a}$
and such that
$a'\in S^{0,a}$
and such that
![]() $\Phi ^{l^a}(D_{a'}^a)$
holds. By hypothesis, this is a b-definable set contained in S and containing a.
$\Phi ^{l^a}(D_{a'}^a)$
holds. By hypothesis, this is a b-definable set contained in S and containing a.
We conclude that
![]() $S=\bigcup _{a\in S}S^a$
is a cover of S by b-definable sets, and so by compactness and saturation, there is a finite sub-cover, say
$S=\bigcup _{a\in S}S^a$
is a cover of S by b-definable sets, and so by compactness and saturation, there is a finite sub-cover, say
![]() $S=S^1\cup \dots \cup S^k$
for
$S=S^1\cup \dots \cup S^k$
for
![]() $S^r=S^{a_r}$
. Indeed, if there was no finite sub-cover, then the partial type expressing
$S^r=S^{a_r}$
. Indeed, if there was no finite sub-cover, then the partial type expressing
![]() $x\in S$
and
$x\in S$
and
![]() $x\notin S^a$
for all
$x\notin S^a$
for all
![]() $a\in S$
is a consistent b-type, and so a realization in M would contradict
$a\in S$
is a consistent b-type, and so a realization in M would contradict
![]() $S=\bigcup _{a\in S}S^a$
.
$S=\bigcup _{a\in S}S^a$
.
Then
![]() $D_{a}$
defined as
$D_{a}$
defined as
![]() $D_{a}^{a_r}$
if
$D_{a}^{a_r}$
if
![]() $a\in S^r\setminus \bigcup _{r'<r}S^{r'}$
satisfies that
$a\in S^r\setminus \bigcup _{r'<r}S^{r'}$
satisfies that
![]() $\{D_{a}\}_{a\in S}$
forms a b-definable family. If we take l such that
$\{D_{a}\}_{a\in S}$
forms a b-definable family. If we take l such that
![]() $l\geq l^{a_1},\dots ,l^{a_k}$
, then we get that
$l\geq l^{a_1},\dots ,l^{a_k}$
, then we get that
![]() $\Phi ^l(D_{a})$
holds for every
$\Phi ^l(D_{a})$
holds for every
![]() $a\in S$
, as required.
$a\in S$
, as required.
Notation 3.4. If
![]() $D\subset E\times F$
, and
$D\subset E\times F$
, and
![]() $a\in E$
, we often denote
$a\in E$
, we often denote
![]() $D_a=\{b\in F: (a,b)\in D\}$
. If
$D_a=\{b\in F: (a,b)\in D\}$
. If
![]() $b\in F$
, we denote, when no ambiguity can occur,
$b\in F$
, we denote, when no ambiguity can occur,
![]() $D_b=\{a\in E: (a,b)\in D\}$
. If
$D_b=\{a\in E: (a,b)\in D\}$
. If
![]() $f:D\to C$
is a function, we let
$f:D\to C$
is a function, we let
![]() $f_a:D_a\to C$
denote the function
$f_a:D_a\to C$
denote the function
![]() $f_a(b)=f(a,b)$
, and similarly,
$f_a(b)=f(a,b)$
, and similarly,
![]() $f_b$
for
$f_b$
for
![]() $b\in F$
.
$b\in F$
.
The positive residue characteristic versions of the multi-variable Taylor Theorem is as follows:
Proposition 3.5. Let K be a 1-h-minimal field of positive residue characteristic, let
![]() $f:U\to K$
be an a-definable function with
$f:U\to K$
be an a-definable function with
![]() $U\subset K^n$
open, and let
$U\subset K^n$
open, and let
![]() $r\in {\mathbb {N}}$
. Then there is an integer m, and a set C, which is closed, a-definable and with
$r\in {\mathbb {N}}$
. Then there is an integer m, and a set C, which is closed, a-definable and with
![]() $\dim (C)<n$
, such that for every open ball,
$\dim (C)<n$
, such that for every open ball,
![]() $B\subseteq U$
m-away from C,
$B\subseteq U$
m-away from C,
![]() $f^{(i)}$
exists in B for every i with
$f^{(i)}$
exists in B for every i with
![]() $|i|\leq r$
, and
$|i|\leq r$
, and
![]() $f^{(i)}$
has constant valuation in B. Moreover,
$f^{(i)}$
has constant valuation in B. Moreover,
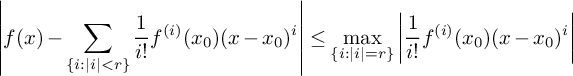 $$ \begin{align*} \left | f(x)-\sum_{\{i:|i|<r\}}\frac{1}{i!}f^{(i)}(x_0)(x-x_0)^i \right | \leq \max_{\{i:|i|=r\}} \left |\frac{1}{i!}f^{(i)}(x_0)(x-x_0)^i \right | \end{align*} $$
$$ \begin{align*} \left | f(x)-\sum_{\{i:|i|<r\}}\frac{1}{i!}f^{(i)}(x_0)(x-x_0)^i \right | \leq \max_{\{i:|i|=r\}} \left |\frac{1}{i!}f^{(i)}(x_0)(x-x_0)^i \right | \end{align*} $$
for every
![]() $x,x_0\in B$
.
$x,x_0\in B$
.
Proof. We proceed by induction on n, the case
![]() $n=1$
being [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Theorem 3.1.2]. Assume the result for n and let
$n=1$
being [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Theorem 3.1.2]. Assume the result for n and let
![]() $f:U\to K$
be an a-definable function with
$f:U\to K$
be an a-definable function with
![]() $U\subset K^n\times K$
open, i a multi-index with
$U\subset K^n\times K$
open, i a multi-index with
![]() $|i|\le r$
. Then for every
$|i|\le r$
. Then for every
![]() $x\in K^n$
, there is a finite
$x\in K^n$
, there is a finite
![]() $ax$
-definable set
$ax$
-definable set
![]() $C_x\subset K$
and an integer
$C_x\subset K$
and an integer
![]() $m_x$
such that
$m_x$
such that
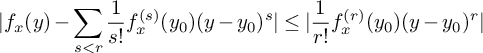 $$ \begin{align} |f_x(y)-\sum_{s<r}\frac{1}{s!}f_x^{(s)}(y_0)(y-y_0)^s| \leq |\frac{1}{r!}f_x^{(r)}(y_0)(y-y_0)^r| \end{align} $$
$$ \begin{align} |f_x(y)-\sum_{s<r}\frac{1}{s!}f_x^{(s)}(y_0)(y-y_0)^s| \leq |\frac{1}{r!}f_x^{(r)}(y_0)(y-y_0)^r| \end{align} $$
for every y and
![]() $y_0$
in an open ball
$y_0$
in an open ball
![]() $m_x$
-away from
$m_x$
-away from
![]() $C_x$
, and such that
$C_x$
, and such that
![]() $|f_x^{(s)}(y)|$
exists and is constant in any such open ball. By a standard compactness argument (see Fact 3.2), we may assume that the
$|f_x^{(s)}(y)|$
exists and is constant in any such open ball. By a standard compactness argument (see Fact 3.2), we may assume that the
![]() $C_x$
are uniformly definable and that there is some
$C_x$
are uniformly definable and that there is some
![]() $m\in {\mathbb {N}}$
such that
$m\in {\mathbb {N}}$
such that
![]() $m_x=m$
for all x. Define
$m_x=m$
for all x. Define
![]() $C=\bigcup _x(\{x\}\times C_x)$
. By induction, for each
$C=\bigcup _x(\{x\}\times C_x)$
. By induction, for each
![]() $y\in K$
, we can approximate the functions
$y\in K$
, we can approximate the functions
![]() $g_{s,y}(x)=f_x^{(s)}(y)$
defined on
$g_{s,y}(x)=f_x^{(s)}(y)$
defined on
![]() $V_y=\mathrm {Int}(U_y\setminus C_y)$
up to order
$V_y=\mathrm {Int}(U_y\setminus C_y)$
up to order
![]() $r-s$
. By a similar application of Fact 3.2, we obtain a natural number
$r-s$
. By a similar application of Fact 3.2, we obtain a natural number
![]() $m'$
and an a-definable family
$m'$
and an a-definable family
![]() $\{D_y\}_{y\in K^n}$
of subsets
$\{D_y\}_{y\in K^n}$
of subsets
![]() $D_y\subseteq V_y$
with
$D_y\subseteq V_y$
with
![]() $\dim (D_y)<n$
such that
$\dim (D_y)<n$
such that
![]() $g_{s,y}^{(i)}$
exists and has constant valuation on any ball
$g_{s,y}^{(i)}$
exists and has constant valuation on any ball
![]() $m'$
-away from
$m'$
-away from
![]() $D_y$
in
$D_y$
in
![]() $V_y$
, for every multi-index i, with
$V_y$
, for every multi-index i, with
![]() $|i|\leq r-s$
. Moreover,
$|i|\leq r-s$
. Moreover,
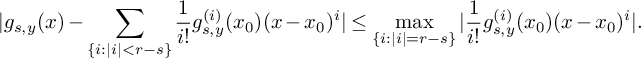 $$ \begin{align} | g_{s,y}(x)-\sum_{\{i:|i|<r-s\}}\frac{1}{i!}g_{s,y}^{(i)}(x_0)(x-x_0)^i | \leq \max_{\{i:|i|=r-s\}} |\frac{1}{i!}g_{s,y}^{(i)}(x_0)(x-x_0)^i|. \end{align} $$
$$ \begin{align} | g_{s,y}(x)-\sum_{\{i:|i|<r-s\}}\frac{1}{i!}g_{s,y}^{(i)}(x_0)(x-x_0)^i | \leq \max_{\{i:|i|=r-s\}} |\frac{1}{i!}g_{s,y}^{(i)}(x_0)(x-x_0)^i|. \end{align} $$
Replacing m and
![]() $m'$
by their maximum, we may assume
$m'$
by their maximum, we may assume
![]() $m=m'$
. Define
$m=m'$
. Define
![]() $D:=\bigcup _y D_y\times \{y\}$
. By additivity of dimension,
$D:=\bigcup _y D_y\times \{y\}$
. By additivity of dimension,
![]() $\dim (C)\le n$
and
$\dim (C)\le n$
and
![]() $\dim (D)\le n$
. Now take
$\dim (D)\le n$
. Now take
![]() $E=C\cup D\cup \bigcup _y (U_y\setminus V_y)\times \{y\}$
. Similar dimension considerations show that
$E=C\cup D\cup \bigcup _y (U_y\setminus V_y)\times \{y\}$
. Similar dimension considerations show that
![]() $\dim (E)<n+1$
.
$\dim (E)<n+1$
.
Note that for
![]() $(x,y)\in U\setminus E$
, we have that, for i and s such that
$(x,y)\in U\setminus E$
, we have that, for i and s such that
![]() $|i|+s\leq r$
,
$|i|+s\leq r$
,
![]() $f^{(i,s)}(x,y)$
and
$f^{(i,s)}(x,y)$
and
![]() $g_{s,y}^{(i)}(x)$
exist and are equal.
$g_{s,y}^{(i)}(x)$
exist and are equal.
Now, for
![]() $x\in K^n$
, define
$x\in K^n$
, define
![]() $W_x=\mathrm {Int}(U_x\setminus E_x)$
, and for the functions
$W_x=\mathrm {Int}(U_x\setminus E_x)$
, and for the functions
![]() $h_{x,s,i}:y\mapsto f^{(i,s)}(x,y)$
with
$h_{x,s,i}:y\mapsto f^{(i,s)}(x,y)$
with
![]() $s+|i|\leq r$
defined on
$s+|i|\leq r$
defined on
![]() $W_x$
, we find a finite set
$W_x$
, we find a finite set
![]() $F_x\subset W_x$
such that
$F_x\subset W_x$
such that
![]() $\{F_x\}_x$
is an a-definable family, and there is an integer
$\{F_x\}_x$
is an a-definable family, and there is an integer
![]() $m'$
, such that in every ball in
$m'$
, such that in every ball in
![]() $W_x$
$W_x$
![]() $m'$
-away from
$m'$
-away from
![]() $F_x$
,
$F_x$
,
![]() $h_{x,s,i}$
has constant valuation. We may assume that
$h_{x,s,i}$
has constant valuation. We may assume that
![]() $m'=m$
as before. Let G be the closure of
$m'=m$
as before. Let G be the closure of
![]() $E\cup \bigcup _x (\{x\}\times F_x)\cup \bigcup _x (\{x\}\times (U_x\setminus W_x))$
. Note that
$E\cup \bigcup _x (\{x\}\times F_x)\cup \bigcup _x (\{x\}\times (U_x\setminus W_x))$
. Note that
![]() $\dim (G)<n+1$
.
$\dim (G)<n+1$
.
Take
![]() $B_1\times B_2$
a ball in U, m-away from G. Then for every
$B_1\times B_2$
a ball in U, m-away from G. Then for every
![]() $x\in B_1$
, we get that
$x\in B_1$
, we get that
![]() $B_2$
is m-away from both
$B_2$
is m-away from both
![]() $C_x$
and
$C_x$
and
![]() $F_x$
and
$F_x$
and
![]() $B_2\subseteq W_x$
. Similarly, for every
$B_2\subseteq W_x$
. Similarly, for every
![]() $y\in B_2$
,
$y\in B_2$
,
![]() $B_1\subseteq V_y$
is m-away from
$B_1\subseteq V_y$
is m-away from
![]() $D_y$
.
$D_y$
.
We conclude that for every
![]() $(x,y)\in B_1\times B_2$
,
$(x,y)\in B_1\times B_2$
,
![]() $f^{(i,s)}(x,y)$
exists and has constant valuation, for every index
$f^{(i,s)}(x,y)$
exists and has constant valuation, for every index
![]() $(i,s)$
such that
$(i,s)$
such that
![]() $|(i,s)|\leq r$
. Indeed, we have for every
$|(i,s)|\leq r$
. Indeed, we have for every
![]() $(x,y), (x',y')\in B_1\times B_2$
that
$(x,y), (x',y')\in B_1\times B_2$
that
as the second equality follows from the condition on
![]() $D_{y'}$
, and the fourth from those on
$D_{y'}$
, and the fourth from those on
![]() $F_x$
and
$F_x$
and
![]() $W_x$
.
$W_x$
.
Now, if
![]() $(x,y)$
and
$(x,y)$
and
![]() $(x_0,y_0)$
are in
$(x_0,y_0)$
are in
![]() $B_1\times B_2$
, then equations 1 and 2 hold, and for the error term of 1, we have
$B_1\times B_2$
, then equations 1 and 2 hold, and for the error term of 1, we have
![]() $|f_x^{(r)}(y_0)|=|f^{(0,r)}(x,y_0)|= |f^{(0,r)}(x_0,y_0)|$
. Denote
$|f_x^{(r)}(y_0)|=|f^{(0,r)}(x,y_0)|= |f^{(0,r)}(x_0,y_0)|$
. Denote
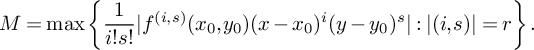 $$\begin{align*}M=\max\left \{\frac{1}{i!s!} |f^{(i,s)}(x_0,y_0)(x-x_0)^i(y-y_0)^s|: |(i,s)|=r\right \}.\end{align*}$$
$$\begin{align*}M=\max\left \{\frac{1}{i!s!} |f^{(i,s)}(x_0,y_0)(x-x_0)^i(y-y_0)^s|: |(i,s)|=r\right \}.\end{align*}$$
Then Equation 1 yields
![]() $|f(x,y)-\sum _{s<r}\frac {1}{s!}f^{(0,s)}(x,y_0)(y-y_0)^s|\leq M$
. Also, from Equation 2, we have that
$|f(x,y)-\sum _{s<r}\frac {1}{s!}f^{(0,s)}(x,y_0)(y-y_0)^s|\leq M$
. Also, from Equation 2, we have that
 $$\begin{align*}\left |\frac{1}{s!}f^{(0,s)}(x,y_0)(y-y_0)^s- \sum_{\{i:|i|<r-s\}}\frac{1}{i!s!}f^{(i,s)}(x_0,y_0)(x-x_0)^i(y-y_0)^s \right | \leq M.\end{align*}$$
$$\begin{align*}\left |\frac{1}{s!}f^{(0,s)}(x,y_0)(y-y_0)^s- \sum_{\{i:|i|<r-s\}}\frac{1}{i!s!}f^{(i,s)}(x_0,y_0)(x-x_0)^i(y-y_0)^s \right | \leq M.\end{align*}$$
Taking the sum over s smaller than r and using the ultrametric inequality, we obtain
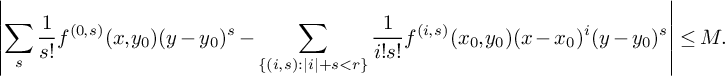 $$\begin{align*}\left |\sum_s \frac{1}{s!}f^{(0,s)}(x,y_0)(y-y_0)^s- \sum_{\{(i,s):|i|+s<r\}}\frac{1}{i!s!}f^{(i,s)}(x_0,y_0)(x-x_0)^i(y-y_0)^s\right |\leq M.\end{align*}$$
$$\begin{align*}\left |\sum_s \frac{1}{s!}f^{(0,s)}(x,y_0)(y-y_0)^s- \sum_{\{(i,s):|i|+s<r\}}\frac{1}{i!s!}f^{(i,s)}(x_0,y_0)(x-x_0)^i(y-y_0)^s\right |\leq M.\end{align*}$$
Summing this with Equation 1 and using the ultrametric inequality once more, we conclude.
As a consequence of the previous theorem, we obtain that partial derivatives of definable functions commute generically.
Corollary 3.6. Suppose
![]() $f:U\to K$
is a definable function for some open
$f:U\to K$
is a definable function for some open
![]() $U\subset K\times K$
. Then there exists a dense open
$U\subset K\times K$
. Then there exists a dense open
![]() $U'\subset U$
such that for every
$U'\subset U$
such that for every
![]() $(x,y)\in U'$
,
$(x,y)\in U'$
,
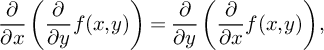 $$\begin{align*}\frac{\partial}{\partial x} \left (\frac{\partial}{\partial y}f(x,y)\right )= \frac{\partial}{\partial y}\left ( \frac{\partial}{\partial x}f(x,y) \right ),\end{align*}$$
$$\begin{align*}\frac{\partial}{\partial x} \left (\frac{\partial}{\partial y}f(x,y)\right )= \frac{\partial}{\partial y}\left ( \frac{\partial}{\partial x}f(x,y) \right ),\end{align*}$$
and, in particular, the terms of the above equation exist in
![]() $U'$
.
$U'$
.
Moreover, if
![]() $f:U\to K$
is such that the partial derivatives
$f:U\to K$
is such that the partial derivatives
![]() $\frac {\partial }{\partial x}\frac {\partial }{\partial y}f(x,y)$
,
$\frac {\partial }{\partial x}\frac {\partial }{\partial y}f(x,y)$
,
![]() $\frac {\partial }{\partial y}\frac {\partial }{\partial x}f(x,y)$
exist and are continuous in U, then they are equal.
$\frac {\partial }{\partial y}\frac {\partial }{\partial x}f(x,y)$
exist and are continuous in U, then they are equal.
Proof. Take a
![]() $1$
-dimensional closed
$1$
-dimensional closed
![]() $C\subset K\times K$
and m an integer as provided by the Taylor approximation property for errors of order
$C\subset K\times K$
and m an integer as provided by the Taylor approximation property for errors of order
![]() $3$
. We may also assume that
$3$
. We may also assume that
![]() $\pi (C)$
and m satisfy the same Taylor approximation property for the function
$\pi (C)$
and m satisfy the same Taylor approximation property for the function
![]() $f\pi $
, where
$f\pi $
, where
![]() $\pi $
is the coordinate permutation
$\pi $
is the coordinate permutation
![]() $(x,y)\mapsto (y,x)$
.
$(x,y)\mapsto (y,x)$
.
Then for
![]() $(x,y),(x_0,y_0)\in B_1\times B_2$
in a ball m-away from C, we obtain (see Definition 2.1 for the big-O notation) that
$(x,y),(x_0,y_0)\in B_1\times B_2$
in a ball m-away from C, we obtain (see Definition 2.1 for the big-O notation) that
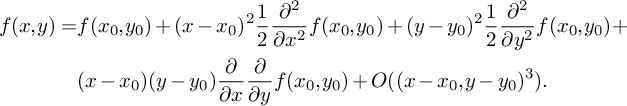 $$ \begin{align*} f(x,y)=& f(x_0,y_0)+ (x-x_0)^2\frac{1}{2}\frac{\partial^2}{\partial x^2}f(x_0,y_0)+ (y-y_0)^2\frac{1}{2}\frac{\partial^2}{\partial y^2}f(x_0,y_0)+ \\ & (x-x_0)(y-y_0)\frac{\partial}{\partial x}\frac{\partial}{\partial y}f(x_0,y_0)+ O((x-x_0,y-y_0)^3). \end{align*} $$
$$ \begin{align*} f(x,y)=& f(x_0,y_0)+ (x-x_0)^2\frac{1}{2}\frac{\partial^2}{\partial x^2}f(x_0,y_0)+ (y-y_0)^2\frac{1}{2}\frac{\partial^2}{\partial y^2}f(x_0,y_0)+ \\ & (x-x_0)(y-y_0)\frac{\partial}{\partial x}\frac{\partial}{\partial y}f(x_0,y_0)+ O((x-x_0,y-y_0)^3). \end{align*} $$
Similarly,
 $$ \begin{align*} f\pi(y,x)=f(x,y)=& f(x_0,y_0)+ (x-x_0)^2\frac{1}{2}\frac{\partial^2}{\partial x^2}f(x_0,y_0)+ (y-y_0)^2\frac{1}{2}\frac{\partial^2}{\partial y^2}f(x_0,y_0)+ \\ & (x-x_0)(y-y_0)\frac{\partial}{\partial y}\frac{\partial}{\partial x}f(x_0,y_0)+ O((x-x_0,y-y_0)^3). \end{align*} $$
$$ \begin{align*} f\pi(y,x)=f(x,y)=& f(x_0,y_0)+ (x-x_0)^2\frac{1}{2}\frac{\partial^2}{\partial x^2}f(x_0,y_0)+ (y-y_0)^2\frac{1}{2}\frac{\partial^2}{\partial y^2}f(x_0,y_0)+ \\ & (x-x_0)(y-y_0)\frac{\partial}{\partial y}\frac{\partial}{\partial x}f(x_0,y_0)+ O((x-x_0,y-y_0)^3). \end{align*} $$
Taking the difference, we obtain
Taking
![]() $h=(x-x_0)=(y-y_0)$
small, we get
$h=(x-x_0)=(y-y_0)$
small, we get
![]() $h^2 (\frac {\partial }{\partial y}\frac {\partial }{\partial x}f(x_0,y_0)- \frac {\partial }{\partial x}\frac {\partial }{\partial y}f(x_0,y_0))= O(h^3)$
, so
$h^2 (\frac {\partial }{\partial y}\frac {\partial }{\partial x}f(x_0,y_0)- \frac {\partial }{\partial x}\frac {\partial }{\partial y}f(x_0,y_0))= O(h^3)$
, so
![]() $\frac {\partial }{\partial y}\frac {\partial }{\partial x}f(x_0,y_0)- \frac {\partial }{\partial x}\frac {\partial }{\partial y}f(x_0,y_0)=O(h)$
. This is only possible when the left-hand side is
$\frac {\partial }{\partial y}\frac {\partial }{\partial x}f(x_0,y_0)- \frac {\partial }{\partial x}\frac {\partial }{\partial y}f(x_0,y_0)=O(h)$
. This is only possible when the left-hand side is
![]() $0$
, as desired.
$0$
, as desired.
The second statement follows from the assumed continuity, as two continuous functions into a Hausdorff space agreeing on a dense subset are equal.
The following notation is intended to provide a cleaner expression for the Taylor approximation of multivariate functions.
Definition 3.7. Let
![]() $m, n$
be positive integers, and
$m, n$
be positive integers, and
![]() $r\in {\mathbb {N}}$
. Let
$r\in {\mathbb {N}}$
. Let
![]() $J=J(r,n)=\{j\in \mathbb {N}^n: |j|=r\}$
. Let
$J=J(r,n)=\{j\in \mathbb {N}^n: |j|=r\}$
. Let
![]() $a=(a_j)_{j\in J}$
be such that
$a=(a_j)_{j\in J}$
be such that
![]() $a_j\in K^m$
for all
$a_j\in K^m$
for all
![]() $j\in J$
. Then, for
$j\in J$
. Then, for
![]() $x\in K^n$
, we define
$x\in K^n$
, we define
![]() $ax^r=\sum \limits _{j\in J}a_jx^j$
, where
$ax^r=\sum \limits _{j\in J}a_jx^j$
, where
![]() $x^j:=\prod _{i=1}^n x_i^{j(i)}$
. Note that
$x^j:=\prod _{i=1}^n x_i^{j(i)}$
. Note that
![]() $x\mapsto ax^r$
is a function
$x\mapsto ax^r$
is a function
![]() $K^n\to K^m$
.
$K^n\to K^m$
.
As an example, consider, in the above notation, the case
![]() $r=1$
. In this case,
$r=1$
. In this case,
![]() $J=\{e_1,\dots , e_n\}$
, and for
$J=\{e_1,\dots , e_n\}$
, and for
![]() $j\in J$
, we have
$j\in J$
, we have
![]() $x^j=x_j$
(where
$x^j=x_j$
(where
![]() $x=(x_1,\dots , x_n)$
), so for
$x=(x_1,\dots , x_n)$
), so for
![]() $a=(a_j)_{j\in J}$
with
$a=(a_j)_{j\in J}$
with
![]() $a_j\in K^m$
, we get that
$a_j\in K^m$
, we get that
![]() $ax=A\cdot x$
, where A is the matrix whose j-th column is
$ax=A\cdot x$
, where A is the matrix whose j-th column is
![]() $a_j$
.
$a_j$
.
In the same spirit, we have the following:
Definition 3.8. Let
![]() $m,n,k$
be positive integers, and
$m,n,k$
be positive integers, and
![]() $r,s\in {\mathbb {N}}$
. Let
$r,s\in {\mathbb {N}}$
. Let
![]() $J_1=J(r,n)$
and
$J_1=J(r,n)$
and
![]() $J_2=J(s,m)$
be as in Definition 3.7. Let
$J_2=J(s,m)$
be as in Definition 3.7. Let
![]() $a=(a_{j,j'})_{j\in J_1,j'\in J_2}$
be such that
$a=(a_{j,j'})_{j\in J_1,j'\in J_2}$
be such that
![]() $a_{j,j'}\in K^k$
. Then, for
$a_{j,j'}\in K^k$
. Then, for
![]() $x\in K^n$
and
$x\in K^n$
and
![]() $y\in K^m$
, we define
$y\in K^m$
, we define
![]() $ax^ry^s=\sum \limits _{j\in J_1,j'\in J_2}a_{j,j'}x^{j}y^{j'}$
. Note that
$ax^ry^s=\sum \limits _{j\in J_1,j'\in J_2}a_{j,j'}x^{j}y^{j'}$
. Note that
![]() $(x,y)\mapsto ax^ry^s$
is a function
$(x,y)\mapsto ax^ry^s$
is a function
![]() $K^n\times K^m\to K^k$
.
$K^n\times K^m\to K^k$
.
As an example, note that the functions
![]() $(x,y)\mapsto axy$
are exactly the bilinear functions
$(x,y)\mapsto axy$
are exactly the bilinear functions
![]() $K^n\times K^m\to K^k$
.
$K^n\times K^m\to K^k$
.
Using the above notation, we introduce the following:
Definition 3.9. Let
![]() $U\subset K^k$
be open,
$U\subset K^k$
be open,
![]() $f:U\to K^m$
a function and
$f:U\to K^m$
a function and
![]() $a\in U$
. We say that f is
$a\in U$
. We say that f is
![]() $P_n$
at a if it is approximable by polynomials of degree n near a in the following sense: there are constants
$P_n$
at a if it is approximable by polynomials of degree n near a in the following sense: there are constants
![]() $b_0,\cdots ,b_n$
such that
$b_0,\cdots ,b_n$
such that
![]() $f(a+x)=\sum _{r\leq n}b_rx^r+O(x^{n+1})$
.
$f(a+x)=\sum _{r\leq n}b_rx^r+O(x^{n+1})$
.
We say f is
![]() $P_n$
in U if it is
$P_n$
in U if it is
![]() $P_n$
at every point of U.
$P_n$
at every point of U.
In view of the example after Definition 3.7, it follows immediately from the definition that a
![]() $P_1$
function is differentiable, and for the coefficient
$P_1$
function is differentiable, and for the coefficient
![]() $b_1$
in the definition, we may take
$b_1$
in the definition, we may take
![]() $f'(a)$
(or, more precisely,
$f'(a)$
(or, more precisely,
![]() $b_1^t=f'(a)$
). Note also that a
$b_1^t=f'(a)$
). Note also that a
![]() $P_n$
function is also
$P_n$
function is also
![]() $P_m$
for every
$P_m$
for every
![]() $m\leq n$
.
$m\leq n$
.
Lemma 3.10. If f is
![]() $P_n$
at a, then for every number
$P_n$
at a, then for every number
![]() $i\leq n$
, the coefficients
$i\leq n$
, the coefficients
![]() $b_i$
in Definition 3.9 are determined by f.
$b_i$
in Definition 3.9 are determined by f.
Proof. The problem readily reduces to the case of f a polynomial restricted to some open neighborhood, U, of the origin. That is, we have to show that if
![]() $\sum _{i\leq n}b_ix^i=O(x^{n+1})$
in any open
$\sum _{i\leq n}b_ix^i=O(x^{n+1})$
in any open
![]() $U\subseteq K^r$
, then
$U\subseteq K^r$
, then
![]() $b_i=0$
for all i. For
$b_i=0$
for all i. For
![]() $x_0$
fixed, let
$x_0$
fixed, let
![]() $x=tx_0$
and consider the single variable polynomial
$x=tx_0$
and consider the single variable polynomial
![]() $P(tx_0)=\sum _{i\le n} (b_ix_0^i)t^i=O(t^{n+1})$
. If we knew the result for
$P(tx_0)=\sum _{i\le n} (b_ix_0^i)t^i=O(t^{n+1})$
. If we knew the result for
![]() $r=1$
, this would give that
$r=1$
, this would give that
![]() $b_ix_0^i=0$
. Since
$b_ix_0^i=0$
. Since
![]() $x_0\in U$
was arbitrary and U contains a cartesian product of r infinite sets, this implies
$x_0\in U$
was arbitrary and U contains a cartesian product of r infinite sets, this implies
![]() $b_i=0$
for all i. So we are reduced to proving the result for
$b_i=0$
for all i. So we are reduced to proving the result for
![]() $r=1$
.
$r=1$
.
In this case, if i is the smallest with
![]() $b_i\neq 0$
, we get
$b_i\neq 0$
, we get
![]() $x^i=O(x^{i+1})$
, which is a contradiction.
$x^i=O(x^{i+1})$
, which is a contradiction.
The next technical definition is only used to obtain the Lie algebra of a definable Lie group; see Proposition 6.19. For the latter, Lemma 3.16 below is key.
We mention that this notion of
![]() $T_n$
was selected to be first order expressible, stronger than
$T_n$
was selected to be first order expressible, stronger than
![]() $P_n$
, and satisfying Propositions 3.12,3.13 and, crucially, Lemma 3.16. Readers willing to accept these results may treat the definition as a black box and skip to the next section.
$P_n$
, and satisfying Propositions 3.12,3.13 and, crucially, Lemma 3.16. Readers willing to accept these results may treat the definition as a black box and skip to the next section.
Definition 3.11. Let
![]() $U\subset K^k$
be open,
$U\subset K^k$
be open,
![]() $f:U\to K^m$
a function and
$f:U\to K^m$
a function and
![]() $a\in U$
. We say f is
$a\in U$
. We say f is
![]() $T_n$
at a if there is
$T_n$
at a if there is
![]() $\gamma \in \Gamma $
such that for every
$\gamma \in \Gamma $
such that for every
![]() $x,x'$
with
$x,x'$
with
![]() $|x-a|,|x'-a|<\gamma $
, we have
$|x-a|,|x'-a|<\gamma $
, we have
![]() $f(x)=\sum _{r\leq n}c_r(x')(x-x')^r+O(x-x')^{n+1}$
for a function
$f(x)=\sum _{r\leq n}c_r(x')(x-x')^r+O(x-x')^{n+1}$
for a function
![]() $c_r$
that is
$c_r$
that is
![]() $P_{n-r}$
at a.
$P_{n-r}$
at a.
We say f is
![]() $T_n$
in U if it is
$T_n$
in U if it is
![]() $T_n$
at every point of U.
$T_n$
at every point of U.
Note that in the previous definition, the constant implicit in the notation
![]() $O(x-x')^{n+1}$
(see Definition 2.1) does not depend on
$O(x-x')^{n+1}$
(see Definition 2.1) does not depend on
![]() $x'$
, so this definition requires some uniformity with respect to the center
$x'$
, so this definition requires some uniformity with respect to the center
![]() $x'$
which is not implied by simply assuming f is
$x'$
which is not implied by simply assuming f is
![]() $P_n$
at every point of a ball around a.
$P_n$
at every point of a ball around a.
Note also that if f is
![]() $T_n$
at
$T_n$
at
![]() $c=(b,a)$
, then, in particular,
$c=(b,a)$
, then, in particular,
![]() $f(z,a+x)=f(z)+f_1(z)x+\cdots +f_n(z)x^n+O(x^{n+1})$
for functions
$f(z,a+x)=f(z)+f_1(z)x+\cdots +f_n(z)x^n+O(x^{n+1})$
for functions
![]() $f_k$
that are
$f_k$
that are
![]() $P_{n-k}$
at b (and a constant in
$P_{n-k}$
at b (and a constant in
![]() $O(x^{n+1})$
uniform in z). This follows from the definition by taking
$O(x^{n+1})$
uniform in z). This follows from the definition by taking
![]() $x=(z,a+x)$
and
$x=(z,a+x)$
and
![]() $x'=(z,a)$
.
$x'=(z,a)$
.
Sums and products of
![]() $P_n$
(resp.
$P_n$
(resp.
![]() $T_n$
) functions are
$T_n$
) functions are
![]() $P_n$
(resp.
$P_n$
(resp.
![]() $T_n$
), and a vector function is
$T_n$
), and a vector function is
![]() $P_n$
(resp.
$P_n$
(resp.
![]() $T_n$
) if and only if its coordinate functions are
$T_n$
) if and only if its coordinate functions are
![]() $P_n$
(resp.
$P_n$
(resp.
![]() $T_n$
).
$T_n$
).
Note also that a
![]() $T_n$
function is
$T_n$
function is
![]() $T_m$
for every
$T_m$
for every
![]() $m<n$
, and a
$m<n$
, and a
![]() $T_1$
function at a is strictly differentiable at a (with
$T_1$
function at a is strictly differentiable at a (with
![]() $f'(a)=c_1(a)$
).
$f'(a)=c_1(a)$
).
We could also require the stronger condition, say
![]() $ST_n$
, defined similarly to
$ST_n$
, defined similarly to
![]() $T_n$
, but requiring inductively the functions
$T_n$
, but requiring inductively the functions
![]() $c_r$
be
$c_r$
be
![]() $ST_{n-r}$
for
$ST_{n-r}$
for
![]() $r=1,\dots ,n$
(the base case
$r=1,\dots ,n$
(the base case
![]() $ST_0=T_0$
). A possible advantage of
$ST_0=T_0$
). A possible advantage of
![]() $ST_n$
is that it can be shown that
$ST_n$
is that it can be shown that
![]() $ST_n$
functions are n-times strictly differentiable. We do not know whether this holds of
$ST_n$
functions are n-times strictly differentiable. We do not know whether this holds of
![]() $T_n$
functions as well. Since all we need is the easy observation that
$T_n$
functions as well. Since all we need is the easy observation that
![]() $T_1$
functions are strictly differentiable, and
$T_1$
functions are strictly differentiable, and
![]() $T_2$
is precisely what is needed to achieve the conclusion of Lemma 3.16, we opted to keep the simpler, though possibly less natural definition.
$T_2$
is precisely what is needed to achieve the conclusion of Lemma 3.16, we opted to keep the simpler, though possibly less natural definition.
Proposition 3.12. If g is
![]() $P_n$
at a and f is
$P_n$
at a and f is
![]() $P_n$
at
$P_n$
at
![]() $g(a)$
then the composition,
$g(a)$
then the composition,
![]() $f\circ g$
is
$f\circ g$
is
![]() $P_n$
at a.
$P_n$
at a.
If g is
![]() $T_n$
at a and f is
$T_n$
at a and f is
![]() $T_n$
at
$T_n$
at
![]() $g(a)$
, then
$g(a)$
, then
![]() $f\circ g$
is
$f\circ g$
is
![]() $T_n$
at a.
$T_n$
at a.
Proof. For the first statement, we write
 $$ \begin{align*} & f(g(a+x))= \\ & f(g(a)+g_1(a)x+...+g_n(a)x^n+O(x^{n+1}))= \\ & f(g(a))+f_1(g(a))h(a,x)+f_2(g(a))h(a,x)^2+...+O(h(a,x)^{n+1})= \\ & fg(a)+b_1(a)x+\cdots+b_n(a)x^n+O(x^{n+1})+O(h(a,x)^{n+1}), \end{align*} $$
$$ \begin{align*} & f(g(a+x))= \\ & f(g(a)+g_1(a)x+...+g_n(a)x^n+O(x^{n+1}))= \\ & f(g(a))+f_1(g(a))h(a,x)+f_2(g(a))h(a,x)^2+...+O(h(a,x)^{n+1})= \\ & fg(a)+b_1(a)x+\cdots+b_n(a)x^n+O(x^{n+1})+O(h(a,x)^{n+1}), \end{align*} $$
where
-
(1)
 $h(a,x)=g(a+x)-g(a)=g_1(a)x+\cdots +g_n(a)x^n+O(x^{n+1})$
$h(a,x)=g(a+x)-g(a)=g_1(a)x+\cdots +g_n(a)x^n+O(x^{n+1})$
-
(2) The second inequality is the application of the assumption that f is
 $P_n$
at
$P_n$
at
 $g(a)$
.
$g(a)$
. -
(3) The coefficients
 $b_i$
arise by expanding the expression
$b_i$
arise by expanding the expression  $$\begin{align*}f_k(a)h(a,x)^k=f_k(a)(g_1(a)x+\cdots+g_n(a)x^n+O(x^{n+1}))^k. \end{align*}$$
$$\begin{align*}f_k(a)h(a,x)^k=f_k(a)(g_1(a)x+\cdots+g_n(a)x^n+O(x^{n+1}))^k. \end{align*}$$
To conclude, we note that, as in the proof of Lemma 3.10,
![]() $h(a,x)=O(x)$
, and so
$h(a,x)=O(x)$
, and so
![]() $O(h(a,x)^{n+1})=O(x^{n+1})$
.
$O(h(a,x)^{n+1})=O(x^{n+1})$
.
The proof of the second statement is, essentially, similar:
 $$ \begin{align*} & f(g(x))=\\ & f(g(x')+g_1(x')(x-x')+...+g_n(x')(x-x')^n+O(x-x')^{n+1})= \\ & f(g(x'))+f_1(g(x'))h(x,x')+f_2(g(x'))h(x,x')^2+...+f_n(g(x'))h(x,x')^n+O(h(x,x')^{n+1})= \\ & f(g(x'))+b_1(x')(x-x')+\cdots+b_n(x')(x-x')^n+O(x-x')^{n+1}, \end{align*} $$
$$ \begin{align*} & f(g(x))=\\ & f(g(x')+g_1(x')(x-x')+...+g_n(x')(x-x')^n+O(x-x')^{n+1})= \\ & f(g(x'))+f_1(g(x'))h(x,x')+f_2(g(x'))h(x,x')^2+...+f_n(g(x'))h(x,x')^n+O(h(x,x')^{n+1})= \\ & f(g(x'))+b_1(x')(x-x')+\cdots+b_n(x')(x-x')^n+O(x-x')^{n+1}, \end{align*} $$
where
![]() $h(x,x')=g(x)-g(x')=g_1(x')(x-x')+\cdots +g_n(x')(x-x')^n+O(x-x')^{n+1}= O(x-x')$
, and the coordinates of the coefficients
$h(x,x')=g(x)-g(x')=g_1(x')(x-x')+\cdots +g_n(x')(x-x')^n+O(x-x')^{n+1}= O(x-x')$
, and the coordinates of the coefficients
![]() $b_k(x')$
are sums and products of the coordinates of the coefficients of
$b_k(x')$
are sums and products of the coordinates of the coefficients of
![]() $f_i(g(x'))$
and
$f_i(g(x'))$
and
![]() $g_j(x')$
with
$g_j(x')$
with
![]() $i,j\leq k$
. By what we have just proved, those are
$i,j\leq k$
. By what we have just proved, those are
![]() $P_{n-i}$
functions. The constant appearing on
$P_{n-i}$
functions. The constant appearing on
![]() $h(x,x')=O(x-x')$
does not depend on
$h(x,x')=O(x-x')$
does not depend on
![]() $x'$
because the
$x'$
because the
![]() $g_i$
are continuous at a. We conclude that the
$g_i$
are continuous at a. We conclude that the
![]() $b_k$
are
$b_k$
are
![]() $P_{n-k}$
at a, as claimed.
$P_{n-k}$
at a, as claimed.
Proposition 3.13. Let K be 1-h-minimal and
![]() $f:U\to K^m$
as definable function. Then there exists
$f:U\to K^m$
as definable function. Then there exists
![]() $U'\subset U$
definable open and dense, such that f is
$U'\subset U$
definable open and dense, such that f is
![]() $T_n$
at every point of
$T_n$
at every point of
![]() $U'$
.
$U'$
.
In particular, for every
![]() $f:U\to K^m$
, there is a definable open dense subset
$f:U\to K^m$
, there is a definable open dense subset
![]() $U'\subset U$
such that f is strictly differentiable in
$U'\subset U$
such that f is strictly differentiable in
![]() $U'$
.
$U'$
.
This follows from Taylor’s approximation theorem (Proposition 3.1 in residue characteristic
![]() $0$
and Proposition 3.5 in positive residue characteristic). The second statement follows because a
$0$
and Proposition 3.5 in positive residue characteristic). The second statement follows because a
![]() $T_1$
function is strictly differentiable.
$T_1$
function is strictly differentiable.
In the next section, we show that a strictly differentiable map with invertible derivative, definable in a 1-h-minimal valued field, is a local homeomorphism. Here, we show that the local inverse is strictly differentiable. We then proceed to showing that the properties
![]() $P_n$
and
$P_n$
and
![]() $T_n$
are also preserved in this local inverse, though this latter fact is not used for the proof of our main results.
$T_n$
are also preserved in this local inverse, though this latter fact is not used for the proof of our main results.
Proposition 3.14. Suppose
![]() $f:U\to V$
is a bijection where
$f:U\to V$
is a bijection where
![]() $U\subset K^n$
and
$U\subset K^n$
and
![]() $V\subset K^n$
are open. Suppose f satisfies
$V\subset K^n$
are open. Suppose f satisfies
![]() $|f(x)-f(y)-(x-y)|<|x-y|$
for
$|f(x)-f(y)-(x-y)|<|x-y|$
for
![]() $x,y\in U$
distinct. Assume f is differentiable at a. Then
$x,y\in U$
distinct. Assume f is differentiable at a. Then
![]() $f'(a)$
is invertible,
$f'(a)$
is invertible,
![]() $f^{-1}$
is differentiable at
$f^{-1}$
is differentiable at
![]() $b=f(a)$
and
$b=f(a)$
and
![]() $(f^{-1})'(b)=f'(f^{-1}(b))^{-1}$
.
$(f^{-1})'(b)=f'(f^{-1}(b))^{-1}$
.
If f is strictly differentiable at a, then
![]() $f^{-1}$
is strictly differentiable at b.
$f^{-1}$
is strictly differentiable at b.
Proof. Note that the hypothesis implies
![]() $|f(x)-f(x')|=|x-x'|$
. This implies that
$|f(x)-f(x')|=|x-x'|$
. This implies that
![]() $f'(a)$
is invertible. Indeed, assume otherwise and take x close to a such that
$f'(a)$
is invertible. Indeed, assume otherwise and take x close to a such that
![]() $f'(a)(x-a)=0$
to get
$f'(a)(x-a)=0$
to get
![]() $|f(x)-f(a)|<|x-a|$
, a contradiction.
$|f(x)-f(a)|<|x-a|$
, a contradiction.
Assume that f is strictly differentiable at a. Take
![]() $\epsilon>0$
in
$\epsilon>0$
in
![]() $\Gamma $
. Then there is
$\Gamma $
. Then there is
![]() $0<r\in \Gamma $
such that if
$0<r\in \Gamma $
such that if
![]() $|x-a|,|x'-a|<r$
, then
$|x-a|,|x'-a|<r$
, then
![]() $|f(x)-f(x')-f'(a)(x-x')|\le \epsilon |x-x'|$
. If we denote
$|f(x)-f(x')-f'(a)(x-x')|\le \epsilon |x-x'|$
. If we denote
![]() $y=f(x)$
and
$y=f(x)$
and
![]() $y'=f(x')$
, then we have
$y'=f(x')$
, then we have
![]() $|y-y'|=|x-x'|$
, so multiplying the above inequality by
$|y-y'|=|x-x'|$
, so multiplying the above inequality by
![]() $f'(a)^{-1}$
, we obtain
$f'(a)^{-1}$
, we obtain
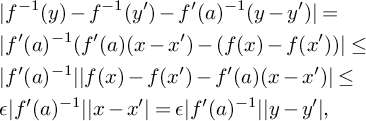 $$ \begin{align*} & |f^{-1}(y)-f^{-1}(y')-f'(a)^{-1}(y-y')|= \\ & |f'(a)^{-1}(f'(a)(x-x')-(f(x)-f(x'))|\le \\ & |f'(a)^{-1}||f(x)-f(x')-f'(a)(x-x')|\le \\ & \epsilon |f'(a)^{-1}||x-x'|= \epsilon |f'(a)^{-1}||y-y'|, \end{align*} $$
$$ \begin{align*} & |f^{-1}(y)-f^{-1}(y')-f'(a)^{-1}(y-y')|= \\ & |f'(a)^{-1}(f'(a)(x-x')-(f(x)-f(x'))|\le \\ & |f'(a)^{-1}||f(x)-f(x')-f'(a)(x-x')|\le \\ & \epsilon |f'(a)^{-1}||x-x'|= \epsilon |f'(a)^{-1}||y-y'|, \end{align*} $$
where, for a linear map, A, represented by the matrix
![]() $(a_{ij})_{i,j}$
, we denote
$(a_{ij})_{i,j}$
, we denote
![]() $|A|=\max _{i,j}|a_{ij}|$
and use the ultra-metric inequality to get
$|A|=\max _{i,j}|a_{ij}|$
and use the ultra-metric inequality to get
![]() $|Ax|\le |A||x|$
, which we apply to obtain the first inequality in the above computation.
$|Ax|\le |A||x|$
, which we apply to obtain the first inequality in the above computation.
So we conclude that
![]() $|f^{-1}(y)-f^{-1}(y')-f'(a)^{-1}(y-y')|\leq \epsilon |f'(a)|^{-1}|y-y'|$
for any
$|f^{-1}(y)-f^{-1}(y')-f'(a)^{-1}(y-y')|\leq \epsilon |f'(a)|^{-1}|y-y'|$
for any
![]() $y,y'$
such that
$y,y'$
such that
![]() $|y-b|=|x-a|<r$
and
$|y-b|=|x-a|<r$
and
![]() $|y'-b|=|x'-a|<r$
. We have thus shown that
$|y'-b|=|x'-a|<r$
. We have thus shown that
![]() $f^{-1}$
is strictly differentiable at b and
$f^{-1}$
is strictly differentiable at b and
![]() $(f^{-1})'(b)=f'(f^{-1}(b))^{-1}$
.
$(f^{-1})'(b)=f'(f^{-1}(b))^{-1}$
.
To show that
![]() $f^{-1}$
is differentiable if f is, substitute
$f^{-1}$
is differentiable if f is, substitute
![]() $x'=a$
in the above argument.
$x'=a$
in the above argument.
Proposition 3.15. Suppose
![]() $f:U\to V$
is a bijection where
$f:U\to V$
is a bijection where
![]() $U\subset K^n$
and
$U\subset K^n$
and
![]() $V\subset K^n$
are open. Suppose f satisfies
$V\subset K^n$
are open. Suppose f satisfies
![]() $|f(x)-f(y)-(x-y)|<|x-y|$
for
$|f(x)-f(y)-(x-y)|<|x-y|$
for
![]() $x,y\in U$
distinct. Then if f is
$x,y\in U$
distinct. Then if f is
![]() $P_n$
(resp.
$P_n$
(resp.
![]() $T_n$
) at b,
$T_n$
) at b,
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $P_n$
(resp.
$P_n$
(resp.
![]() $T_n$
) at
$T_n$
) at
![]() $f(b)$
.
$f(b)$
.
Proof. Denote
![]() $a=f(b)$
. Note that the hypothesis implies then
$a=f(b)$
. Note that the hypothesis implies then
![]() $|f(x)-f(y)|=|x-y|$
for all distinct
$|f(x)-f(y)|=|x-y|$
for all distinct
![]() $x,y\in U$
, so the inverse map
$x,y\in U$
, so the inverse map
![]() $f^{-1}$
is continuous and in fact satisfies
$f^{-1}$
is continuous and in fact satisfies
![]() $|f^{-1}(x)-f^{-1}(y)|=|x-y|$
for distinct
$|f^{-1}(x)-f^{-1}(y)|=|x-y|$
for distinct
![]() $x,y\in V$
. In particular,
$x,y\in V$
. In particular,
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $T_0$
in V.
$T_0$
in V.
Now, assume that f is
![]() $P_n$
at b, with
$P_n$
at b, with
![]() $n\ge 1$
. In particular, by Proposition 3.14, it is differentiable and
$n\ge 1$
. In particular, by Proposition 3.14, it is differentiable and
![]() $f'(b)$
is invertible.
$f'(b)$
is invertible.
Apply the fact that f is
![]() $P_n$
(and see also the discussion following the definition) to get
$P_n$
(and see also the discussion following the definition) to get
Rearranging, we get
Putting
![]() $y=f^{-1}(x)$
, and remembering
$y=f^{-1}(x)$
, and remembering
![]() $x-a=O(y-b)$
, we conclude
$x-a=O(y-b)$
, we conclude
for some constants
![]() $c_i(a)$
.
$c_i(a)$
.
Next, we proceed to showing (by induction on
![]() $k\le n$
) that
$k\le n$
) that
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $P_k$
. As
$P_k$
. As
![]() $P_0$
follows from the equality
$P_0$
follows from the equality
![]() $|f^{-1}(x)-f^{-1}(y)|=|x-y|$
, we assume that
$|f^{-1}(x)-f^{-1}(y)|=|x-y|$
, we assume that
![]() $k\geq 1$
. So suppose
$k\geq 1$
. So suppose
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $P_{k-1}$
. Using this, we can write
$P_{k-1}$
. Using this, we can write
![]() $f^{-1}(x)-f^{-1}(a)=\sum _{1\leq j<k}b_j(a)(x-a)^j+O(x-a)^k$
and apply a direct computation to obtain that
$f^{-1}(x)-f^{-1}(a)=\sum _{1\leq j<k}b_j(a)(x-a)^j+O(x-a)^k$
and apply a direct computation to obtain that
for some constants
![]() $d_{ij}$
. Note that as
$d_{ij}$
. Note that as
![]() $i\ge 2$
, we obtain the improved error
$i\ge 2$
, we obtain the improved error
![]() $O(x-a)^{k+1}$
. Substituting this in
$O(x-a)^{k+1}$
. Substituting this in
![]() $(\diamond )$
, it follows that
$(\diamond )$
, it follows that
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $P^k$
, as required.
$P^k$
, as required.
Now suppose f is
![]() $T_n$
at b. The proof in this case is similar:
$T_n$
at b. The proof in this case is similar:
so, as above, if
![]() $f^{-1}(x)$
is
$f^{-1}(x)$
is
![]() $T_{k-1}$
, we obtain
$T_{k-1}$
, we obtain
Here, note that
![]() $f'$
is
$f'$
is
![]() $P_{n-1}$
at b and so
$P_{n-1}$
at b and so
![]() $f'(f^{-1}(x'))^{-1}$
is
$f'(f^{-1}(x'))^{-1}$
is
![]() $P_{k-1}$
at a. Also, following the above argument, we see that the coordinates of
$P_{k-1}$
at a. Also, following the above argument, we see that the coordinates of
![]() $d_i(x')$
are sums and products of functions of the form
$d_i(x')$
are sums and products of functions of the form
![]() $b_{i'}(x')$
with
$b_{i'}(x')$
with
![]() $1\leq i'<i$
, for
$1\leq i'<i$
, for
![]() $b_{i'}(x')$
a
$b_{i'}(x')$
a
![]() $P_{k-1-i'}$
function at a (by the induction hypothesis that
$P_{k-1-i'}$
function at a (by the induction hypothesis that
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $T_{k-1}$
), and functions of the form
$T_{k-1}$
), and functions of the form
![]() $c_{i'}(f^{-1}(x'))$
for
$c_{i'}(f^{-1}(x'))$
for
![]() $c_{i'}(y')$
a
$c_{i'}(y')$
a
![]() $P_{k-i'}$
function at b,
$P_{k-i'}$
function at b,
![]() $i'\leq i$
(by the assumption that f is
$i'\leq i$
(by the assumption that f is
![]() $T_n$
). So
$T_n$
). So
![]() $d_i(x')$
is
$d_i(x')$
is
![]() $P_{k-i}$
at a.
$P_{k-i}$
at a.
The next lemma will be important in our study of the differential structure of definable groups. For the statement, recall that
![]() $O_x$
means that the constant implicit in the notation depends on x; see Definition 2.1. In the statement and proof, we are also using the notation
$O_x$
means that the constant implicit in the notation depends on x; see Definition 2.1. In the statement and proof, we are also using the notation
![]() $axy$
introduced in Definition 3.8.
$axy$
introduced in Definition 3.8.
Lemma 3.16. Let
![]() $f:U\times V\to K^r$
be a definable function, where
$f:U\times V\to K^r$
be a definable function, where
![]() $U\subset K^n$
and
$U\subset K^n$
and
![]() $V\subset K^m$
are open sets around
$V\subset K^m$
are open sets around
![]() $0$
. Suppose
$0$
. Suppose
![]() $f(x,y)$
is
$f(x,y)$
is
![]() $T_2$
at
$T_2$
at
![]() $(0,0)$
, and
$(0,0)$
, and
![]() $f(x,y)=O(x,y)^3$
. If
$f(x,y)=O(x,y)^3$
. If
![]() $axy+f(x,y)=O_x(y^2)$
, then
$axy+f(x,y)=O_x(y^2)$
, then
![]() $a=0$
.
$a=0$
.
Proof. By the definition of
![]() $T_2$
(with
$T_2$
(with
![]() $x=x'$
,
$x=x'$
,
![]() $y'=0$
), we get
$y'=0$
), we get
![]() $f(x,y)=f_0(x)+f_1(x)y+f_2(x)y^2+O(y^3)$
for
$f(x,y)=f_0(x)+f_1(x)y+f_2(x)y^2+O(y^3)$
for
![]() $f_2$
a
$f_2$
a
![]() $P_0$
function at
$P_0$
function at
![]() $0$
,
$0$
,
![]() $f_1$
a
$f_1$
a
![]() $P_1$
function at
$P_1$
function at
![]() $0$
and
$0$
and
![]() $f_0$
a
$f_0$
a
![]() $P_2$
function at
$P_2$
function at
![]() $0$
. Fixing x and expanding the Taylor polynomial of
$0$
. Fixing x and expanding the Taylor polynomial of
![]() $f(x,y)$
, the uniqueness of Taylor coefficients (Lemma 3.10) gives, using our assumption,
$f(x,y)$
, the uniqueness of Taylor coefficients (Lemma 3.10) gives, using our assumption,
![]() $axy+f_0(x)+f_1(x)y=0$
.
$axy+f_0(x)+f_1(x)y=0$
.
Expanding
![]() $f_0,f_1,f_2$
around
$f_0,f_1,f_2$
around
![]() $0$
and keeping in mind
$0$
and keeping in mind
![]() $f(x,y)= O(x,y)^3$
, we get
$f(x,y)= O(x,y)^3$
, we get
![]() $f_0(x)= O(x^3)$
and
$f_0(x)= O(x^3)$
and
![]() $f_1(x)= O(x^2)$
. Indeed, we have
$f_1(x)= O(x^2)$
. Indeed, we have
![]() $f_0(x)=b_0+b_1x+b_2x^2+O(x^3)$
,
$f_0(x)=b_0+b_1x+b_2x^2+O(x^3)$
,
![]() $f_1(x)=c_0+c_1x+O(x^2)$
and
$f_1(x)=c_0+c_1x+O(x^2)$
and
![]() $f_2=d_0+O(x)$
, so
$f_2=d_0+O(x)$
, so
![]() $f(x,y)=b_0+b_1x+b_2x^2+c_0y+c_1xy+d_0y^2+O(x,y)^3=O(x,y)^3$
. So from the uniqueness of the Taylor coefficients, we get
$f(x,y)=b_0+b_1x+b_2x^2+c_0y+c_1xy+d_0y^2+O(x,y)^3=O(x,y)^3$
. So from the uniqueness of the Taylor coefficients, we get
![]() $b_0=b_1=b_2=c_0=c_1=0$
.
$b_0=b_1=b_2=c_0=c_1=0$
.
Now from
![]() $axy=O(x,y)^3$
, we get
$axy=O(x,y)^3$
, we get
![]() $a=0$
, by the uniqueness of Taylor coefficients again.
$a=0$
, by the uniqueness of Taylor coefficients again.
4. Strictly differentiable definable maps
In this section, we prove an inverse function theorem for definable strictly differentiable maps in a 1-h-minimal valued field. This is done by adapting a standard argument from real analysis using Banach’s fixed point theorem. In the present section, we use definable spherical completeness to obtain a definable version of Banach’s fixed point theorem, implying, almost formally, the desired inverse function theorem. From the inverse function theorem, we deduce results on the local structure of immersions and submersions in the usual way. We then proceed to proving a generic version of the theorem on the local structure of functions of constant rank (Proposition 4.11). This last result is obtained only generically. The reason is that definable functions whose partial derivative with respect to a variable x is
![]() $0$
on an open set. U need not be locally constant in x in U, as shown in Example 4.7 below. For that reason, we give a different argument for a weaker result (see Proposition 4.8) and the discussion preceding it.
$0$
on an open set. U need not be locally constant in x in U, as shown in Example 4.7 below. For that reason, we give a different argument for a weaker result (see Proposition 4.8) and the discussion preceding it.
Throughout the rest of this section, we fix an
![]() $\aleph _0$
-saturated 1-h-minimal valued field K.
$\aleph _0$
-saturated 1-h-minimal valued field K.
We start with a fixed point theorem, mentioned in [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Remark 2.7.3]. We first note that a version of definable spherical completeness of
![]() $1$
-h-minimal fields ([Reference Cluckers, Halupczok and Rideau-Kikuchi4, Lemma 2.7.1]) holds in positive residue characteristic:
$1$
-h-minimal fields ([Reference Cluckers, Halupczok and Rideau-Kikuchi4, Lemma 2.7.1]) holds in positive residue characteristic:
Lemma 4.1. Suppose K has positive residue characteristic p. Suppose
![]() $\{B_i\}_i$
is a definable chain of open balls or a definable chain of closed balls. Suppose, further, that for every i, there is j such that
$\{B_i\}_i$
is a definable chain of open balls or a definable chain of closed balls. Suppose, further, that for every i, there is j such that
![]() $\text {rad}(B_j)\leq |p|\text {rad}(B_i)$
. Then
$\text {rad}(B_j)\leq |p|\text {rad}(B_i)$
. Then
![]() $\bigcap _i B_i\neq \emptyset $
.
$\bigcap _i B_i\neq \emptyset $
.
Proof. The proof is similar to spherical completeness in residue characteristic
![]() $0$
; see Lemma 2.7.1 of [Reference Cluckers, Halupczok and Rideau-Kikuchi4]. It is enough consider the
$0$
; see Lemma 2.7.1 of [Reference Cluckers, Halupczok and Rideau-Kikuchi4]. It is enough consider the
![]() $1$
-dimensional case since the higher dimensional case follows by considering the coordinate projections. Note also that our assumption implies that the chain
$1$
-dimensional case since the higher dimensional case follows by considering the coordinate projections. Note also that our assumption implies that the chain
![]() $\{B_i\}$
has no minimal element (as such an element would have valuative radius
$\{B_i\}$
has no minimal element (as such an element would have valuative radius
![]() $0$
).
$0$
).
The closed case follows from the open case as follows: given a definable chain
![]() $\{B_i\}_{i\in I}$
of closed balls, for each i, let
$\{B_i\}_{i\in I}$
of closed balls, for each i, let
![]() $r_i$
be the valuative radius of
$r_i$
be the valuative radius of
![]() $B_i$
and let
$B_i$
and let
![]() $B_i^{\prime }$
be the unique open ball
$B_i^{\prime }$
be the unique open ball
![]() $B\subseteq B_i$
of valuative radius
$B\subseteq B_i$
of valuative radius
![]() $r_i$
with the additional property that
$r_i$
with the additional property that
![]() $B\supseteq B_j$
for all
$B\supseteq B_j$
for all
![]() $j<i$
. Obviously,
$j<i$
. Obviously,
![]() $\bigcap _i B_i=\bigcap _i B_i^{\prime }$
(unless the chain
$\bigcap _i B_i=\bigcap _i B_i^{\prime }$
(unless the chain
![]() $B_i$
has a minimal element, in which case there is nothing to prove).
$B_i$
has a minimal element, in which case there is nothing to prove).
Note that, in the above notation, the map
![]() $B_i\mapsto r_i$
is injective, so there is no harm assuming that
$B_i\mapsto r_i$
is injective, so there is no harm assuming that
![]() $\{B_i\}$
is indexed by a subset of
$\{B_i\}$
is indexed by a subset of
![]() $\Gamma $
. Thus, our chain
$\Gamma $
. Thus, our chain
![]() $\{B_i\}$
has index set interpretable in
$\{B_i\}$
has index set interpretable in
![]() $RV$
, so by [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Proposition 2.3.2], there is a finite set C m-preparing the chain
$RV$
, so by [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Proposition 2.3.2], there is a finite set C m-preparing the chain
![]() $\{B_i\}$
for some
$\{B_i\}$
for some
![]() $m\in {\mathbb {N}}$
. We claim that
$m\in {\mathbb {N}}$
. We claim that
![]() $C\cap B_i\neq \emptyset $
for all
$C\cap B_i\neq \emptyset $
for all
![]() $i\in I$
. This would finish the proof since C is finite. Assume, therefore, that this is not the case, and let
$i\in I$
. This would finish the proof since C is finite. Assume, therefore, that this is not the case, and let
![]() $i_0\in I$
be such that
$i_0\in I$
be such that
![]() $B_{i_0}\cap C=\emptyset $
. By assumption, we can find
$B_{i_0}\cap C=\emptyset $
. By assumption, we can find
![]() $i<i_0$
such that
$i<i_0$
such that
![]() $r_i<|p^m|r_{i_0}$
. Then
$r_i<|p^m|r_{i_0}$
. Then
![]() $B_i$
is a ball m-away from C, and since our chain has no minimal element, any ball
$B_i$
is a ball m-away from C, and since our chain has no minimal element, any ball
![]() $B\varsubsetneq B_i$
that is an element of our chain is not m-prepared by C, a contradiction.
$B\varsubsetneq B_i$
that is an element of our chain is not m-prepared by C, a contradiction.
Note that by [Reference Bradley-Williams and Halupczok3, Exanple 1.5], infinitely ramified
![]() $1$
-h-minimal fields of positive residue characteristic need not be definably spherically model complete. Thus, the extra condition in the assumption of the above lemma is not superfluous.
$1$
-h-minimal fields of positive residue characteristic need not be definably spherically model complete. Thus, the extra condition in the assumption of the above lemma is not superfluous.
Proposition 4.2. Let
![]() $B_r=\{x\in K^n: |x|\leq r\}$
. Suppose
$B_r=\{x\in K^n: |x|\leq r\}$
. Suppose
![]() $f:B_r\to B_r$
is a definable function. Assume that for distinct
$f:B_r\to B_r$
is a definable function. Assume that for distinct
![]() $x,y\in B_r$
, we have
$x,y\in B_r$
, we have
-
(1)
 $|f(x)-f(y)|<|x-y|$
if the residue characteristic is
$|f(x)-f(y)|<|x-y|$
if the residue characteristic is
 $0$
.
$0$
. -
(2)
 $|f(x)-f(y)|\leq |p||x-y|$
if the residue characteristic is
$|f(x)-f(y)|\leq |p||x-y|$
if the residue characteristic is
 $p>0$
.
$p>0$
.
Then f has a unique fixed point in
![]() $B_r$
.
$B_r$
.
Proof. Uniqueness is immediate from the hypothesis. For existence, take the family of balls of the form
![]() $B(a)_{|f(a)-a|}$
. It is a definable chain of balls indexed by
$B(a)_{|f(a)-a|}$
. It is a definable chain of balls indexed by
![]() $a\in B_r$
. Indeed, if
$a\in B_r$
. Indeed, if
![]() $a,b\in B_r$
are distinct and the balls are disjoint, then
$a,b\in B_r$
are distinct and the balls are disjoint, then
![]() $|f(a)-f(b)|=|a-b|$
, as the distance of points in disjoint balls does not change. Note that in positive residue characteristic, one has the additional hypothesis in Lemma 4.1 because
$|f(a)-f(b)|=|a-b|$
, as the distance of points in disjoint balls does not change. Note that in positive residue characteristic, one has the additional hypothesis in Lemma 4.1 because
![]() $|f(f(a))-f(a)|\leq |p||f(a)-a|$
, by assumption 2 on f.
$|f(f(a))-f(a)|\leq |p||f(a)-a|$
, by assumption 2 on f.
By the appropriate version of definable spherical completeness of 1-h-minimal fields (Lemma 2.7.1 of [Reference Cluckers, Halupczok and Rideau-Kikuchi4] for residue characteristic
![]() $0$
, Lemma 4.1 otherwise), we obtain a point x in the intersection of all balls. Then x is a fixed point of f. Indeed, if we assume otherwise, then for
$0$
, Lemma 4.1 otherwise), we obtain a point x in the intersection of all balls. Then x is a fixed point of f. Indeed, if we assume otherwise, then for
![]() $y=f(x)$
, we have
$y=f(x)$
, we have
![]() $|f(y)-y|<|f(x)-x|$
by the hypothesis. However, if a is arbitrary then, as
$|f(y)-y|<|f(x)-x|$
by the hypothesis. However, if a is arbitrary then, as
![]() $x\in B(a)_{|f(a)-a|}$
, one has
$x\in B(a)_{|f(a)-a|}$
, one has
![]() $|f(x)-f(a)|\leq |x-a|\leq |f(a)-a|$
and so
$|f(x)-f(a)|\leq |x-a|\leq |f(a)-a|$
and so
![]() $|f(x)-x|\leq |f(a)-a|$
. This is a contradiction and finishes the proof.
$|f(x)-x|\leq |f(a)-a|$
. This is a contradiction and finishes the proof.
Just as in real analysis, this fixed point theorem implies an inverse function theorem.
Proposition 4.3. Suppose
![]() $f:U\to K^n$
is a definable function from an open set
$f:U\to K^n$
is a definable function from an open set
![]() $U\subset K^n$
satisfying the following ‘bilipschitz condition’: for every distinct
$U\subset K^n$
satisfying the following ‘bilipschitz condition’: for every distinct
![]() $x,y\in U$
,
$x,y\in U$
,
-
(1)
 $|f(x)-f(y)-(x-y)|<|x-y|$
if the residue characteristic is
$|f(x)-f(y)-(x-y)|<|x-y|$
if the residue characteristic is
 $0$
.
$0$
. -
(2)
 $|f(x)-f(y)-(x-y)\leq |p||x-y|$
if the residue characteristic is
$|f(x)-f(y)-(x-y)\leq |p||x-y|$
if the residue characteristic is
 $p>0$
.
$p>0$
.
Then
![]() $f(U)$
is open and f is a homeomorphism from U to
$f(U)$
is open and f is a homeomorphism from U to
![]() $f(U)$
. If f is (strictly) differentiable, then
$f(U)$
. If f is (strictly) differentiable, then
![]() $f^{-1}$
is (strictly) differentiable.
$f^{-1}$
is (strictly) differentiable.
Proof. Injectivity of the map follows directly from the hypothesis. The same assumptions also imply that if
![]() $x,y\in U$
are distinct, then
$x,y\in U$
are distinct, then
![]() $|f(x)-f(y)|=|x-y|$
, implying continuity of the inverse.
$|f(x)-f(y)|=|x-y|$
, implying continuity of the inverse.
The main difficulty is showing that
![]() $f(U)$
is open. Translating, we may assume
$f(U)$
is open. Translating, we may assume
![]() $0\in U$
and
$0\in U$
and
![]() $f(0)=0$
. We have to find an open neighborhood of
$f(0)=0$
. We have to find an open neighborhood of
![]() $0$
in
$0$
in
![]() $f(U)$
. Take
$f(U)$
. Take
![]() $r>0$
such that
$r>0$
such that
![]() $0\in B_r\subset U$
. Then
$0\in B_r\subset U$
. Then
![]() $B_{r}\subset f(U)$
. Indeed, if
$B_{r}\subset f(U)$
. Indeed, if
![]() $|a|\leq r$
, then, by the same reasoning as above, the function
$|a|\leq r$
, then, by the same reasoning as above, the function
![]() $g(x)=x+a-f(x)$
satisfies
$g(x)=x+a-f(x)$
satisfies
![]() $g(B_r)\subset B_r$
. By the assumptions on f, this implies that g satisfies the hypothesis of Proposition 4.2. So
$g(B_r)\subset B_r$
. By the assumptions on f, this implies that g satisfies the hypothesis of Proposition 4.2. So
![]() $g(x_0)=x_0$
for some
$g(x_0)=x_0$
for some
![]() $x_0$
, namely,
$x_0$
, namely,
![]() $a=f(x_0)$
, as claimed.
$a=f(x_0)$
, as claimed.
Differentiability (and strict differentiability) of
![]() $f^{-1}$
now follow from 3.14.
$f^{-1}$
now follow from 3.14.
We can finally formulate and prove the inverse function theorem for
![]() $1$
-h-minimal fields:
$1$
-h-minimal fields:
Proposition 4.4. Suppose
![]() $f:U\to K^n$
is a definable function from an open set
$f:U\to K^n$
is a definable function from an open set
![]() $U\subset K^n$
. Suppose f is strictly differentiable at a and
$U\subset K^n$
. Suppose f is strictly differentiable at a and
![]() $f'(a)$
is invertible. Then there is an open set
$f'(a)$
is invertible. Then there is an open set
![]() $V\subseteq U$
around a such that
$V\subseteq U$
around a such that
![]() $f(V)$
is open and
$f(V)$
is open and
![]() $f:V\to f(V)$
is a bijection whose inverse is strictly differentiable at
$f:V\to f(V)$
is a bijection whose inverse is strictly differentiable at
![]() $f(a)$
.
$f(a)$
.
Proof. By the definition of strict differentiability, the function
![]() $f'(a)^{-1}f$
satisfies the hypothesis of the previous proposition in a small open ball around a. The conclusion follows.
$f'(a)^{-1}f$
satisfies the hypothesis of the previous proposition in a small open ball around a. The conclusion follows.
We do not know whether a definable function,
![]() $f:U\to K$
, with continuous partial derivatives, but such that f is not strictly differentiable in U, could exist.Footnote 2 Clearly, sums, products and compositions of strictly differentiable functions are strictly differentiable, and so are locally analytic functions. Moreover, strict differentiability is first order definable and therefore extends to elementary extensions. Also, by the generic Taylor approximation theorem, in the
$f:U\to K$
, with continuous partial derivatives, but such that f is not strictly differentiable in U, could exist.Footnote 2 Clearly, sums, products and compositions of strictly differentiable functions are strictly differentiable, and so are locally analytic functions. Moreover, strict differentiability is first order definable and therefore extends to elementary extensions. Also, by the generic Taylor approximation theorem, in the
![]() $1$
-h-minimal context, any definable function in an open subset of
$1$
-h-minimal context, any definable function in an open subset of
![]() $K^n$
is strictly differentiable in a dense open subset. See Proposition 3.13.
$K^n$
is strictly differentiable in a dense open subset. See Proposition 3.13.
Our next goal is to study definable functions of constant rank. We first note that without the assumption of definability, a strictly differentiable function whose derivative vanishes identically need not be locally constant:
Example 4.5. Consider a function
![]() $f:\mathcal {O}\to \mathcal {O}$
that is locally constant in
$f:\mathcal {O}\to \mathcal {O}$
that is locally constant in
![]() $B\setminus \{0\}$
but near
$B\setminus \{0\}$
but near
![]() $0$
, it grows like
$0$
, it grows like
![]() $x^2$
. Such a function f will be strictly differentiable, with
$x^2$
. Such a function f will be strictly differentiable, with
![]() $f'\equiv 0$
, but f is not locally constant at
$f'\equiv 0$
, but f is not locally constant at
![]() $0$
.
$0$
.
Roughly, a function as in the above example involves an infinite number of choices, so it is not definable. In contrast, we have the following:
Proposition 4.6. Let
![]() $f:U\to K^m$
be a function definable in an open set
$f:U\to K^m$
be a function definable in an open set
![]() $U\subset K^n$
. Assume f is continuous. Assume f is differentiable with derivative
$U\subset K^n$
. Assume f is continuous. Assume f is differentiable with derivative
![]() $0$
on an open dense subset of U. Then f is locally constant with finite image.
$0$
on an open dense subset of U. Then f is locally constant with finite image.
Proof. We proceed by induction on n, the dimension of the domain. We may assume
![]() $m=1$
.
$m=1$
.
First, assume
![]() $n=1$
. By the valuative Jacobian property in [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Corollary 3.1.6] and [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Corollary 3.1.3], there is a finite set
$n=1$
. By the valuative Jacobian property in [Reference Cluckers, Halupczok and Rideau-Kikuchi4, Corollary 3.1.6] and [Reference Cluckers, Halupczok, Rideau-Kikuchi and Vermeulen5, Corollary 3.1.3], there is a finite set
![]() $C\subset U$
such that in
$C\subset U$
such that in
![]() $U\setminus C$
the function f is locally constant. This implies that the fibers of
$U\setminus C$
the function f is locally constant. This implies that the fibers of
![]() $f|_{U\setminus C}$
are of dimension 1, and so the image of f is finite. As f is continuous, it is locally constant; the fibers form a finite partition of closed and so open sets on which f is constant.
$f|_{U\setminus C}$
are of dimension 1, and so the image of f is finite. As f is continuous, it is locally constant; the fibers form a finite partition of closed and so open sets on which f is constant.
Now assume the proposition is valid for n, and suppose
![]() $U\subset K^n\times K$
. We denote
$U\subset K^n\times K$
. We denote
![]() $\pi _1:K^n\times K\to K^n$
the projection onto the first factor and
$\pi _1:K^n\times K\to K^n$
the projection onto the first factor and
![]() $\pi _2:K^n\times K\to K$
the projection onto the second factor.
$\pi _2:K^n\times K\to K$
the projection onto the second factor.
Let
![]() $V\subset U$
be an open dense subset such that f is differentiable at V with derivative
$V\subset U$
be an open dense subset such that f is differentiable at V with derivative
![]() $0$
. Denote
$0$
. Denote
![]() $C=U\setminus V$
. Let
$C=U\setminus V$
. Let
![]() $T=\{x\in K^n\mid \dim (\pi _1^{-1}(x)\cap C)=1\}$
. Then
$T=\{x\in K^n\mid \dim (\pi _1^{-1}(x)\cap C)=1\}$
. Then
![]() $\dim (T)<n$
. We conclude that there is an open dense set
$\dim (T)<n$
. We conclude that there is an open dense set
![]() $W\subset K^{n}$
such that
$W\subset K^{n}$
such that
![]() $\dim (\pi _1^{-1}(x)\cap C)=0$
for all
$\dim (\pi _1^{-1}(x)\cap C)=0$
for all
![]() $x\in W$
. Similarly, there is an open dense set
$x\in W$
. Similarly, there is an open dense set
![]() $P\subset K$
such that
$P\subset K$
such that
![]() $\dim (\pi _2^{-1}(x)\cap C)<n$
for every
$\dim (\pi _2^{-1}(x)\cap C)<n$
for every
![]() $x\in P$
. Shrinking V to
$x\in P$
. Shrinking V to
![]() $V\cap \pi _1^{-1}(W)\cap \pi _2^{-1}(P)$
, we may assume that if
$V\cap \pi _1^{-1}(W)\cap \pi _2^{-1}(P)$
, we may assume that if
![]() $(x,y)\in V$
, then
$(x,y)\in V$
, then
![]() $V_x$
is an open dense subset of
$V_x$
is an open dense subset of
![]() $U_x$
and
$U_x$
and
![]() $V_y$
is an open dense subset of
$V_y$
is an open dense subset of
![]() $U_y$
. By the induction hypothesis and the
$U_y$
. By the induction hypothesis and the
![]() $n=1$
case, we conclude that
$n=1$
case, we conclude that
![]() $f_x$
and
$f_x$
and
![]() $f_y$
are locally constant. This implies that the fiber
$f_y$
are locally constant. This implies that the fiber
![]() $f^{-1}f(x,y)$
has dimension
$f^{-1}f(x,y)$
has dimension
![]() $n+1$
. Indeed, if B is an open neighborhood of y on which
$n+1$
. Indeed, if B is an open neighborhood of y on which
![]() $f_x$
is constant and for each
$f_x$
is constant and for each
![]() $y'\in B$
we take
$y'\in B$
we take
![]() $R_{y'}\subset U_{x}$
an open neighborhood of x on which
$R_{y'}\subset U_{x}$
an open neighborhood of x on which
![]() $f_{y'}$
is constant, then f is constant on
$f_{y'}$
is constant, then f is constant on
![]() $\bigcup _{y'\in B} R_{y'}\times \{y'\}$
. By dimension considerations, we conclude that the image
$\bigcup _{y'\in B} R_{y'}\times \{y'\}$
. By dimension considerations, we conclude that the image
![]() $f(V)$
is finite. As f is continuous,
$f(V)$
is finite. As f is continuous,
![]() $f^{-1}f(V)$
is closed in U, and as V is dense in U, we conclude
$f^{-1}f(V)$
is closed in U, and as V is dense in U, we conclude
![]() $f(U)=f(V)$
is finite. As f is continuous, we conclude f is locally constant as before.
$f(U)=f(V)$
is finite. As f is continuous, we conclude f is locally constant as before.
Below, we let
![]() $D_yf(x,y)$
be the differential of the function
$D_yf(x,y)$
be the differential of the function
![]() $f_x$
, given by
$f_x$
, given by
![]() $f_x(y)=f(x,y)$
; we call this the derivative of f with respect to y (where y can be a tuple of variables).
$f_x(y)=f(x,y)$
; we call this the derivative of f with respect to y (where y can be a tuple of variables).
Given the previous proposition, we may expect that a definable strictly differentiable function
![]() $f:U\to K^m$
with open domain
$f:U\to K^m$
with open domain
![]() $U\subset K^r\times K^s$
and satisfying that
$U\subset K^r\times K^s$
and satisfying that
![]() $D_yf(x,y)=0$
is locally of the form
$D_yf(x,y)=0$
is locally of the form
![]() $f(x,y)=g(x)$
. Unfortunately, this is not true.
$f(x,y)=g(x)$
. Unfortunately, this is not true.
Example 4.7. Take
![]() $f:\mathcal {O}\times \mathcal {O}\to \mathcal {O}$
defined by
$f:\mathcal {O}\times \mathcal {O}\to \mathcal {O}$
defined by
![]() $f(x,y)=0$
if
$f(x,y)=0$
if
![]() $|y|> |x|$
and
$|y|> |x|$
and
![]() $f(x,y)=x^2$
if
$f(x,y)=x^2$
if
![]() $|y|\leq |x|$
. Then f is strictly differentiable,
$|y|\leq |x|$
. Then f is strictly differentiable,
![]() $f(x,\cdot )$
is locally constant, but f is not of the form
$f(x,\cdot )$
is locally constant, but f is not of the form
![]() $g(x)$
near
$g(x)$
near
![]() $(0,0)$
.
$(0,0)$
.
It is due to this pathology that the conclusion of Proposition 4.11 below only holds generically.
Proposition 4.8. Suppose
![]() $U\subset K^n$
,
$U\subset K^n$
,
![]() $V\subset K^r$
are open and
$V\subset K^r$
are open and
![]() $f:U\times V\to K^m$
is a definable function such that f is continuous and
$f:U\times V\to K^m$
is a definable function such that f is continuous and
![]() $D_yf=0$
on a dense open subset of
$D_yf=0$
on a dense open subset of
![]() $\operatorname {\mathrm {dom}}(f)$
. Then there exists an open dense set
$\operatorname {\mathrm {dom}}(f)$
. Then there exists an open dense set
![]() $U'\subset U$
such that
$U'\subset U$
such that
![]() $f|_{U'\times V}$
is locally of the form
$f|_{U'\times V}$
is locally of the form
![]() $g(x)$
.
$g(x)$
.
Proof. The set D of points
![]() $x\in U$
such that for every point of
$x\in U$
such that for every point of
![]() $\{x\}\times V$
f is locally of the form
$\{x\}\times V$
f is locally of the form
![]() $g(x)$
is definable. More precisely,
$g(x)$
is definable. More precisely,
![]() $x\in D$
exactly when for all
$x\in D$
exactly when for all
![]() $y\in V$
, there exists an open ball
$y\in V$
, there exists an open ball
![]() $B\ni (x,y)$
, such that for all
$B\ni (x,y)$
, such that for all
![]() $(x',y'), (x',y")\in B$
, we have
$(x',y'), (x',y")\in B$
, we have
![]() $f(x',y')=f(x',y")$
. Thus, the statement that D has dense interior in U is a first order expressible property, so we may assume that
$f(x',y')=f(x',y")$
. Thus, the statement that D has dense interior in U is a first order expressible property, so we may assume that
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
; see Fact 2.5 and the subsequent remark.
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
; see Fact 2.5 and the subsequent remark.
In the course of the proof, we may replace U by a dense open subset a finite number of times. Fix
![]() $W\subset U\times V$
, a dense open set where f is differentiable and its derivative with respect to y is
$W\subset U\times V$
, a dense open set where f is differentiable and its derivative with respect to y is
![]() $0$
. Shrinking U, we may assume
$0$
. Shrinking U, we may assume
![]() $W_x\subset V$
is dense, open for all
$W_x\subset V$
is dense, open for all
![]() $x\in U$
. By Proposition 4.6, we know that
$x\in U$
. By Proposition 4.6, we know that
![]() $f_x$
is locally constant with finite image for every
$f_x$
is locally constant with finite image for every
![]() $x\in U$
(recall that
$x\in U$
(recall that
![]() $f_x(y):=f(x,y)$
). The sets
$f_x(y):=f(x,y)$
). The sets
![]() $\mathrm {Im}(f_x)$
form a definable family of finite sets indexed by
$\mathrm {Im}(f_x)$
form a definable family of finite sets indexed by
![]() $x\in U$
, so there is a uniform bound, n, on their cardinalities. Denoting
$x\in U$
, so there is a uniform bound, n, on their cardinalities. Denoting
![]() $A_k=\{x\in U: |\mathrm {Im}(f_x)|=k\}$
, we have
$A_k=\{x\in U: |\mathrm {Im}(f_x)|=k\}$
, we have
![]() $U=A_1\cup \cdots \cup A_n$
, so the union of the interiors of the
$U=A_1\cup \cdots \cup A_n$
, so the union of the interiors of the
![]() $A_k$
form a dense open subset of U. So we may assume that
$A_k$
form a dense open subset of U. So we may assume that
![]() $|\mathrm {Im}(f_x)|=k$
for all x and some fixed k. Since we assumed that
$|\mathrm {Im}(f_x)|=k$
for all x and some fixed k. Since we assumed that
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, there are definable functions
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, there are definable functions
![]() $r_1,\dots , r_k:U\to K^m$
such that
$r_1,\dots , r_k:U\to K^m$
such that
![]() $\{r_1(x),\dots ,r_k(x)\}=\mathrm {Im}(f_x)$
. By generic continuity of definable functions (Proposition 2.12), we may assume that
$\{r_1(x),\dots ,r_k(x)\}=\mathrm {Im}(f_x)$
. By generic continuity of definable functions (Proposition 2.12), we may assume that
![]() $r_i$
are all continuous. Then the sets
$r_i$
are all continuous. Then the sets
![]() $B_i=\{(x,y): f(x,y)=r_i(x)\}$
form a finite partition of
$B_i=\{(x,y): f(x,y)=r_i(x)\}$
form a finite partition of
![]() $U\times V$
into closed, and so open subsets.
$U\times V$
into closed, and so open subsets.
The next two results, describing the local structure of definable maps of full rank, are standard applications of the inverse function theorem:
Proposition 4.9. Suppose
![]() $U\subset K^k$
is a definable open set and
$U\subset K^k$
is a definable open set and
![]() $f:U\to K^k\times K^r$
is a definable, strictly differentiable map. Suppose that for some
$f:U\to K^k\times K^r$
is a definable, strictly differentiable map. Suppose that for some
![]() $a\in U$
, the derivative
$a\in U$
, the derivative
![]() $f'(a)$
has full rank. Then there is a ball
$f'(a)$
has full rank. Then there is a ball
![]() $a\in B\subset U$
, a ball
$a\in B\subset U$
, a ball
![]() $B_2\ni 0$
, a definable open set
$B_2\ni 0$
, a definable open set
![]() $V\subset K^k\times K^r$
and a definable strict diffeomorphism
$V\subset K^k\times K^r$
and a definable strict diffeomorphism
![]() $\varphi :V\to B\times B_2$
such that
$\varphi :V\to B\times B_2$
such that
![]() $f(B)\subset V$
and the composition
$f(B)\subset V$
and the composition
![]() $\varphi f:B\to B\times B_2$
is the inclusion
$\varphi f:B\to B\times B_2$
is the inclusion
![]() $b\mapsto (b,0)$
.
$b\mapsto (b,0)$
.
Proof. After a coordinate permutation in the target, we may assume the principal
![]() $k\times k$
minor of
$k\times k$
minor of
![]() $f'(a)$
is invertible. Consider the function
$f'(a)$
is invertible. Consider the function
![]() $g:U\times K^r\to K^k\times K^r$
defined as
$g:U\times K^r\to K^k\times K^r$
defined as
![]() $g(x,y)=f(x)+(0,y)$
. Then g is strictly differentiable and has invertible derivative at
$g(x,y)=f(x)+(0,y)$
. Then g is strictly differentiable and has invertible derivative at
![]() $(a,0)$
so by the inverse function theorem, Proposition 4.4, we can find a ball B around a and a ball
$(a,0)$
so by the inverse function theorem, Proposition 4.4, we can find a ball B around a and a ball
![]() $B_2$
around
$B_2$
around
![]() $0$
, and open set
$0$
, and open set
![]() $f(a)\in V$
such that g restrict to a strict diffeomorphism
$f(a)\in V$
such that g restrict to a strict diffeomorphism
![]() $g:B\times B_2\to V$
. If
$g:B\times B_2\to V$
. If
![]() $i:B\to B\times B_2$
is the inclusion
$i:B\to B\times B_2$
is the inclusion
![]() $i(b)=(b,0)$
, then we get that
$i(b)=(b,0)$
, then we get that
![]() $gi=f$
, so we conclude the statement is valid with
$gi=f$
, so we conclude the statement is valid with
![]() $\varphi =g^{-1}$
.
$\varphi =g^{-1}$
.
Proposition 4.10. Suppose
![]() $U\subset K^k\times K^r$
is a definable open set and
$U\subset K^k\times K^r$
is a definable open set and
![]() $f:U\to K^k$
is a definable strictly differentiable map. Let
$f:U\to K^k$
is a definable strictly differentiable map. Let
![]() $a\in U$
. Suppose
$a\in U$
. Suppose
![]() $f'(a)$
has full rank. Then there exists a definable open set
$f'(a)$
has full rank. Then there exists a definable open set
![]() $a\in U'\subset U$
, a ball
$a\in U'\subset U$
, a ball
![]() $f(a)\in B$
, a ball
$f(a)\in B$
, a ball
![]() $B_2\subseteq K^r$
and a definable strict diffeomorphism
$B_2\subseteq K^r$
and a definable strict diffeomorphism
![]() $\varphi :B\times B_2\to U'$
, such that
$\varphi :B\times B_2\to U'$
, such that
![]() $f(U')\subset B$
and the composition
$f(U')\subset B$
and the composition
![]() $f\varphi :B\times B_2\to B$
is the projection
$f\varphi :B\times B_2\to B$
is the projection
![]() $(b,c)\mapsto b$
.
$(b,c)\mapsto b$
.
Proof. After applying a coordinate permutation to U, we may assume that the principal
![]() $k\times k$
minor of
$k\times k$
minor of
![]() $f'(a)$
is invertible.
$f'(a)$
is invertible.
Consider the function
![]() $g:U\to K^k\times K^r$
defined as
$g:U\to K^k\times K^r$
defined as
![]() $g(x,y)=(f(x,y),y)$
. Then g is strictly differentiable with invertible differential, so by the inverse function theorem, Proposition 4.4, there is an open set
$g(x,y)=(f(x,y),y)$
. Then g is strictly differentiable with invertible differential, so by the inverse function theorem, Proposition 4.4, there is an open set
![]() $a\in U'\subset U$
such that
$a\in U'\subset U$
such that
![]() $g(U')$
is open and
$g(U')$
is open and
![]() $g:U'\to g(U')$
is a strict diffeomorphism.
$g:U'\to g(U')$
is a strict diffeomorphism.
Shrinking
![]() $U'$
, we may assume
$U'$
, we may assume
![]() $g(U')=B\times B_2$
is a product of two balls. Then if
$g(U')=B\times B_2$
is a product of two balls. Then if
![]() $p:B\times B_2\to B$
is the projection
$p:B\times B_2\to B$
is the projection
![]() $p(b,c)=b$
, we get that
$p(b,c)=b$
, we get that
![]() $pg=f$
, and so the statement is valid with
$pg=f$
, and so the statement is valid with
![]() $\varphi =g^{-1}$
.
$\varphi =g^{-1}$
.
We can finally prove our result on the local structure of definable functions of constant rank:
Proposition 4.11. Let
![]() $U\subset K^k\times K^r$
and
$U\subset K^k\times K^r$
and
![]() $V\subset K^k\times K^s$
be open definable sets and let
$V\subset K^k\times K^s$
be open definable sets and let
![]() $f:U\to V$
be a definable strictly differentiable map such that for all
$f:U\to V$
be a definable strictly differentiable map such that for all
![]() $a\in U$
, the rank of
$a\in U$
, the rank of
![]() $f'(a)$
is constant equal to k. Then there exist
$f'(a)$
is constant equal to k. Then there exist
![]() $U'\subset U$
and
$U'\subset U$
and
![]() $V'\subset V$
definable open sets, such that
$V'\subset V$
definable open sets, such that
![]() $f(U')\subset V'$
, and there are definable strict diffeomorphisms
$f(U')\subset V'$
, and there are definable strict diffeomorphisms
![]() $\varphi _1:B_1\times B_2\to U'$
and
$\varphi _1:B_1\times B_2\to U'$
and
![]() $\varphi _2:V'\to B_1\times B_3$
, such that the composition
$\varphi _2:V'\to B_1\times B_3$
, such that the composition
![]() $\varphi _2f\varphi _1:B_1\times B_2\to B_1\times B_3$
is the map
$\varphi _2f\varphi _1:B_1\times B_2\to B_1\times B_3$
is the map
![]() $(a,b)\mapsto (a,0)$
.
$(a,b)\mapsto (a,0)$
.
Proof. Take a point
![]() $(b,c)\in U$
. After a coordinate permutation in U and V, we may assume
$(b,c)\in U$
. After a coordinate permutation in U and V, we may assume
![]() $f'(b,c)$
has its first
$f'(b,c)$
has its first
![]() $k\times k$
minor invertible. Then by the theorem on submersions, Proposition 4.10, applied to the composition of
$k\times k$
minor invertible. Then by the theorem on submersions, Proposition 4.10, applied to the composition of
![]() $f:U\to K^k\times K^s$
with the projection
$f:U\to K^k\times K^s$
with the projection
![]() $K^k\times K^s\to K^k$
onto the first factor, we may assume (absorbing the diffeomorphism
$K^k\times K^s\to K^k$
onto the first factor, we may assume (absorbing the diffeomorphism
![]() $\varphi _1$
provided by that proposition) that U is of the form
$\varphi _1$
provided by that proposition) that U is of the form
![]() $B_1\times B_2$
and f is of the form
$B_1\times B_2$
and f is of the form
![]() ${f(x,y)=(x,g(x,y))}$
. As
${f(x,y)=(x,g(x,y))}$
. As
![]() $f'$
has constant rank equal to k, we conclude that
$f'$
has constant rank equal to k, we conclude that
![]() $D_yg=0$
. By Proposition 4.8, we may assume
$D_yg=0$
. By Proposition 4.8, we may assume
![]() $g(x,y)$
is of the form
$g(x,y)$
is of the form
![]() $g(x,y)=g(x)$
(after passing, if needed, to smaller open sub-balls of
$g(x,y)=g(x)$
(after passing, if needed, to smaller open sub-balls of
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, not necessarily containing
$B_2$
, not necessarily containing
![]() $(b,c)$
). Now the function
$(b,c)$
). Now the function
![]() ${h:B_1\to K^k\times K^s}$
defined by
${h:B_1\to K^k\times K^s}$
defined by
![]() $h(x)=(x,g(x))$
is a definable strictly differentiable immersion, so by the theorem on immersions 4.9, we may, after shrinking
$h(x)=(x,g(x))$
is a definable strictly differentiable immersion, so by the theorem on immersions 4.9, we may, after shrinking
![]() $B_1$
and composing with a definable diffeomorphism
$B_1$
and composing with a definable diffeomorphism
![]() $\varphi _2$
in the target, assume that h is of the form
$\varphi _2$
in the target, assume that h is of the form
![]() $h(x)=(x,0)$
. This finishes the proof.
$h(x)=(x,0)$
. This finishes the proof.
5. Strictly differentiable definable manifolds
In this section, we introduce several variants of definable manifolds in a 1-h-minimal field. Those are manifolds covered by a finite number of definable charts, with compatibility functions of various kinds.
Throughout, we keep the convention that K is an
![]() $\aleph _0$
-saturated
$\aleph _0$
-saturated
![]() $1$
-h-minimal field. In case
$1$
-h-minimal field. In case
![]() $\operatorname {\mathrm {acl}}_K$
is not the same as
$\operatorname {\mathrm {acl}}_K$
is not the same as
![]() $\operatorname {\mathrm {dcl}}_K$
, it is better to take ‘étale domains’ instead of open subsets of
$\operatorname {\mathrm {dcl}}_K$
, it is better to take ‘étale domains’ instead of open subsets of
![]() $K^n$
as the local model of the manifold. This is because the cell decomposition, as provided by Proposition 2.15, decomposes a definable set into a finite number of pieces, each of which is only a finite cover of an open set, instead of an open set. We describe this notion formally below:
$K^n$
as the local model of the manifold. This is because the cell decomposition, as provided by Proposition 2.15, decomposes a definable set into a finite number of pieces, each of which is only a finite cover of an open set, instead of an open set. We describe this notion formally below:
Definition 5.1. Let
![]() $S\subset K^m$
. A definable function
$S\subset K^m$
. A definable function
![]() $f:S\to K^n$
is (topologically) étale if it is a local homeomorphism. In other words, for every
$f:S\to K^n$
is (topologically) étale if it is a local homeomorphism. In other words, for every
![]() $x\in S$
, there is a ball
$x\in S$
, there is a ball
![]() $B\ni x$
such that
$B\ni x$
such that
![]() $f(B\cap S)$
is open and the inverse map
$f(B\cap S)$
is open and the inverse map
![]() $f(B\cap S)\to B\cap S\to K^m$
is continuous.
$f(B\cap S)\to B\cap S\to K^m$
is continuous.
Informally, we think of étale maps as similar to open immersions and will denote such maps accordingly (e.g.,
![]() $i:U\to K^n$
). We now proceed to describing the differential structure of étale maps (or, rather, étale domains):
$i:U\to K^n$
). We now proceed to describing the differential structure of étale maps (or, rather, étale domains):
Definition 5.2. Suppose
![]() $i:U\to K^n$
and
$i:U\to K^n$
and
![]() $j:V\to K^m$
are étale maps. A definable function
$j:V\to K^m$
are étale maps. A definable function
![]() $f:U\to V$
is strictly differentiable at
$f:U\to V$
is strictly differentiable at
![]() $x\in U$
if there are balls
$x\in U$
if there are balls
![]() $x\in B$
and
$x\in B$
and
![]() $f(x)\in B'$
such that
$f(x)\in B'$
such that
![]() $i:B\cap U\to i(B\cap U)$
,
$i:B\cap U\to i(B\cap U)$
,
![]() $j:B'\cap V\to j(B'\cap V)$
are homeomorphisms onto open sets, such that
$j:B'\cap V\to j(B'\cap V)$
are homeomorphisms onto open sets, such that
![]() $f(B\cap U)\subset B'\cap V$
, and the map
$f(B\cap U)\subset B'\cap V$
, and the map
![]() $i(B\cap U)\xrightarrow {i^{-1}} B\cap U\xrightarrow {f} B'\cap V\xrightarrow {j} j(B'\cap V)$
is strictly differentiable at
$i(B\cap U)\xrightarrow {i^{-1}} B\cap U\xrightarrow {f} B'\cap V\xrightarrow {j} j(B'\cap V)$
is strictly differentiable at
![]() $i(x)$
. In this case, the derivative
$i(x)$
. In this case, the derivative
![]() $f'(x)$
is defined as the derivative of
$f'(x)$
is defined as the derivative of
![]() $i(B\cap U)\to j(B'\cap V)$
.
$i(B\cap U)\to j(B'\cap V)$
.
The function
![]() $f:U\to V$
is
$f:U\to V$
is
![]() $T_k$
at x if the composition
$T_k$
at x if the composition
![]() $i(B\cap U)\to j(B'\cap V)$
is
$i(B\cap U)\to j(B'\cap V)$
is
![]() $T_k$
at
$T_k$
at
![]() $i(x)$
.
$i(x)$
.
Note that with this definition, the given inclusion
![]() $U\subset K^r$
is not necessarily strictly differentiable because the local inverses
$U\subset K^r$
is not necessarily strictly differentiable because the local inverses
![]() $i(U\cap B)\to K^r$
of the map
$i(U\cap B)\to K^r$
of the map
![]() $i:U\to K^n$
are only topological embeddings, so not necessarily strictly differentiable.
$i:U\to K^n$
are only topological embeddings, so not necessarily strictly differentiable.
For the rest of this section, let
![]() $\mathcal {P}$
stand for any one of the following adjectives: topological, strictly differentiable or
$\mathcal {P}$
stand for any one of the following adjectives: topological, strictly differentiable or
![]() $T_n$
.
$T_n$
.
Definition 5.3. A definable weak
![]() $\mathcal {P}$
-n-manifold is a definable set, M, equipped with a finite number of definable injections,
$\mathcal {P}$
-n-manifold is a definable set, M, equipped with a finite number of definable injections,
![]() $\varphi _i:U_i\to M$
, and each
$\varphi _i:U_i\to M$
, and each
![]() $U_i$
comes equipped with an étale map
$U_i$
comes equipped with an étale map
![]() $r_i:U_i\to K^n$
. We require further that the sets
$r_i:U_i\to K^n$
. We require further that the sets
![]() $U_{ij}:=\varphi _i^{-1}(\varphi _j(U_j))$
are open in
$U_{ij}:=\varphi _i^{-1}(\varphi _j(U_j))$
are open in
![]() $U_i$
and that the transition maps
$U_i$
and that the transition maps
![]() $U_{ij}\to U_{ji}$
,
$U_{ij}\to U_{ji}$
,
![]() $ \varphi _j^{-1}\varphi _i$
are
$ \varphi _j^{-1}\varphi _i$
are
![]() $\mathcal {P}$
-maps. We call the
$\mathcal {P}$
-maps. We call the
![]() $(U_i,\varphi _i)$
appearing in this definition the charts of M.
$(U_i,\varphi _i)$
appearing in this definition the charts of M.
We further define the following:
-
(1) A definable weak
 $\mathcal {P}$
-manifold is a weak
$\mathcal {P}$
-manifold is a weak
 $\mathcal {P}$
-n-manifold for some n.
$\mathcal {P}$
-n-manifold for some n. -
(2) A definable weak
 $\mathcal {P}$
-manifold is equipped with a topology making the structure maps,
$\mathcal {P}$
-manifold is equipped with a topology making the structure maps,
 $\varphi _i$
, open immersions.
$\varphi _i$
, open immersions. -
(3) A morphism of definable weak
 $\mathcal {P}$
-manifolds is a definable function
$\mathcal {P}$
-manifolds is a definable function
 $f:M\to N$
, such that for any charts
$f:M\to N$
, such that for any charts
 $\varphi _i:U_i\to M$
and
$\varphi _i:U_i\to M$
and
 $\tau _j:V_j\to N$
, the set
$\tau _j:V_j\to N$
, the set
 $W_{ij}=\varphi _if^{-1}\tau _j(V_j)$
is open in
$W_{ij}=\varphi _if^{-1}\tau _j(V_j)$
is open in
 $U_i$
and the map
$U_i$
and the map
 $W_{ij}\to V_j$
given by
$W_{ij}\to V_j$
given by
 $x\mapsto \tau _j^{-1}f\varphi _i(x)$
is a
$x\mapsto \tau _j^{-1}f\varphi _i(x)$
is a
 $\mathcal {P}$
-map.
$\mathcal {P}$
-map. -
(4) A definable
 $\mathcal {P}$
-n-manifold is a definable weak
$\mathcal {P}$
-n-manifold is a definable weak
 $\mathcal {P}$
-n-manifold, where the
$\mathcal {P}$
-n-manifold, where the
 $U_i$
are open subsets of
$U_i$
are open subsets of
 $K^n$
(and the maps
$K^n$
(and the maps
 $U_i\to K^n$
are inclusions).
$U_i\to K^n$
are inclusions). -
(5) A morphism of definable
 $\mathcal {P}$
-manifolds is a morphism of weak definable
$\mathcal {P}$
-manifolds is a morphism of weak definable
 $\mathcal {P}$
-manifolds.
$\mathcal {P}$
-manifolds.
The last two definitions introduce the categories of definable (weak)
![]() $\mathcal {P}$
-n-manifolds, hence also the notion of isomorphism.
$\mathcal {P}$
-n-manifolds, hence also the notion of isomorphism.
It is common to identify two manifold structures on the same set if the identity map on the underlying set is an isomorphism. We prefer not to do this, and simply treat them as isomorphic objects in the category. The resulting category is, of course, equivalent.
Definable weak manifolds are, immediately from the definition, (abstract) manifolds over K. As such, definable differentiable weak manifolds inherit the classical differential structure. For the sake of completeness, we recall the relevant definitions:
Definition 5.4. If M is a definable strictly differentiable weak manifold and
![]() $x\in M$
, then the tangent space of M at x,
$x\in M$
, then the tangent space of M at x,
![]() $T_x(M)$
is
$T_x(M)$
is
![]() $(\bigsqcup _i T_i)/E$
, where the disjoint union is over the charts
$(\bigsqcup _i T_i)/E$
, where the disjoint union is over the charts
![]() $(U_i,\varphi _i)$
around x,
$(U_i,\varphi _i)$
around x,
![]() $T_i=K^n$
(which we informally think of as the tangent space of
$T_i=K^n$
(which we informally think of as the tangent space of
![]() $\varphi _i^{-1}(x)$
in
$\varphi _i^{-1}(x)$
in
![]() $U_i$
), and the equivalence relation E results from identifying
$U_i$
), and the equivalence relation E results from identifying
![]() $v\in T_i$
with
$v\in T_i$
with
![]() $(\varphi _j^{-1}\varphi _i)'(\varphi _i^{-1}(x))(v)\in T_j$
.
$(\varphi _j^{-1}\varphi _i)'(\varphi _i^{-1}(x))(v)\in T_j$
.
For a strictly differentiable definable morphism
![]() $f:M\to N$
of definable strictly differentiable weak manifolds, we have a map of K-vector spaces
$f:M\to N$
of definable strictly differentiable weak manifolds, we have a map of K-vector spaces
![]() $f'(x):T_x(M)\to T_{f(x)}(N)$
given by the differential of the map appearing in Definition 5.3(3) above.
$f'(x):T_x(M)\to T_{f(x)}(N)$
given by the differential of the map appearing in Definition 5.3(3) above.
As usual, once we have a chart around a point in a weak strictly differentiable manifold, we get an identification of
![]() $T_x(M)$
with
$T_x(M)$
with
![]() $K^n$
, but distinct charts may give distinct isomorphisms.
$K^n$
, but distinct charts may give distinct isomorphisms.
The map
![]() $(M,x)\mapsto T_x(M)$
from pointed definable weak
$(M,x)\mapsto T_x(M)$
from pointed definable weak
![]() $\mathcal {P}$
-n-manifolds to K-vector spaces is a functor or, more precisely, it is the map on objects of a functor (with the obvious definition of the category of pointed weak
$\mathcal {P}$
-n-manifolds to K-vector spaces is a functor or, more precisely, it is the map on objects of a functor (with the obvious definition of the category of pointed weak
![]() $\mathcal {P}$
-n-manifolds). In particular, two isomorphic objects
$\mathcal {P}$
-n-manifolds). In particular, two isomorphic objects
![]() $(M,x)$
and
$(M,x)$
and
![]() $(M',x')$
have isomorphic tangent spaces
$(M',x')$
have isomorphic tangent spaces
![]() $T_x(M)$
and
$T_x(M)$
and
![]() $T_{x'}(M')$
.
$T_{x'}(M')$
.
Definition 5.5. A definable (weak)
![]() $\mathcal {P}$
-Lie group is a group object in the category of definable (weak)
$\mathcal {P}$
-Lie group is a group object in the category of definable (weak)
![]() $\mathcal {P}$
-manifolds.
$\mathcal {P}$
-manifolds.
Lemma 5.6. Suppose
![]() $i:U\to K^n$
and
$i:U\to K^n$
and
![]() $j:V\to K^m$
are étale and
$j:V\to K^m$
are étale and
![]() $f:U\to V$
is a definable map. Then f is continuous in an open dense subset of U.
$f:U\to V$
is a definable map. Then f is continuous in an open dense subset of U.
Also, f is strictly differentiable, and
![]() $T_k$
in an open dense subset of U.
$T_k$
in an open dense subset of U.
Proof. For the statement about continuity, note that V has the subspace topology (of
![]() $V\subset K^r$
), so we may assume
$V\subset K^r$
), so we may assume
![]() $V=K^r$
. If we denote
$V=K^r$
. If we denote
![]() $U'$
the interior (relative to U) of the set of points of U where f is continuous, then in every ball B where i is a homeomorphism
$U'$
the interior (relative to U) of the set of points of U where f is continuous, then in every ball B where i is a homeomorphism
![]() $i:B\cap U\to i(B\cap U)$
, we get that
$i:B\cap U\to i(B\cap U)$
, we get that
![]() $B\cap U'$
is dense in
$B\cap U'$
is dense in
![]() $B\cap U$
, by generic continuity of definable functions. We conclude that
$B\cap U$
, by generic continuity of definable functions. We conclude that
![]() $U'$
is dense as required.
$U'$
is dense as required.
For strict differentiability and
![]() $T_k$
, by the above, we may assume that f is continuous. Let
$T_k$
, by the above, we may assume that f is continuous. Let
![]() $U'$
be the interior of the set of all points where
$U'$
be the interior of the set of all points where
![]() $f:U\to V$
is strictly differentiable and
$f:U\to V$
is strictly differentiable and
![]() $T_k$
. This is a definable open set. By generic differentiability and generic
$T_k$
. This is a definable open set. By generic differentiability and generic
![]() $T_k$
property for functions defined on open sets, for every point
$T_k$
property for functions defined on open sets, for every point
![]() $x\in U$
, there is an open ball
$x\in U$
, there is an open ball
![]() $B\ni x$
, such that
$B\ni x$
, such that
![]() $B\cap U'$
is dense in
$B\cap U'$
is dense in
![]() $U\cap B$
. Thus, we conclude that
$U\cap B$
. Thus, we conclude that
![]() $U'$
is dense in U.
$U'$
is dense in U.
Note that the previous lemma implies that a (weak) definable topological manifold M contains an open dense subset
![]() $U\subset M$
, which admits a structure of a (weak) definable
$U\subset M$
, which admits a structure of a (weak) definable
![]() $T_n$
manifold extending the given (weak) definable topological manifold structure. As a consequence of Proposition 5.7 below, this structure on U is unique up to restriction to a dense open subset and isomorphism. More precisely, if
$T_n$
manifold extending the given (weak) definable topological manifold structure. As a consequence of Proposition 5.7 below, this structure on U is unique up to restriction to a dense open subset and isomorphism. More precisely, if
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
are two structures of
$\tau _2$
are two structures of
![]() $T_n$
-manifold such that the identity map
$T_n$
-manifold such that the identity map
![]() $i:(U,\tau _1)\to (U,\tau _2)$
is an isomorphism of weak definable topological manifolds, there exists
$i:(U,\tau _1)\to (U,\tau _2)$
is an isomorphism of weak definable topological manifolds, there exists
![]() $V\subset U$
open and dense such that the restriction
$V\subset U$
open and dense such that the restriction
![]() $i:(V,\tau _1)\to (V,\tau _2)$
is an isomorphism of weak definable
$i:(V,\tau _1)\to (V,\tau _2)$
is an isomorphism of weak definable
![]() $T_n$
-manifolds. For that reason, several of the statements below hold (essentially unaltered) for definable weak manifolds (without further assumptions on differentiability or
$T_n$
-manifolds. For that reason, several of the statements below hold (essentially unaltered) for definable weak manifolds (without further assumptions on differentiability or
![]() $T_n$
). For the sake of clarity of the exposition, we keep these assumptions.
$T_n$
). For the sake of clarity of the exposition, we keep these assumptions.
Proposition 5.7. If
![]() $f:M\to N$
is a definable function and M, N are definable weak
$f:M\to N$
is a definable function and M, N are definable weak
![]() $\mathcal {P}$
-manifolds, then f is a
$\mathcal {P}$
-manifolds, then f is a
![]() $\mathcal {P}$
-map in an open dense set of M.
$\mathcal {P}$
-map in an open dense set of M.
Proof. Considering the charts in M, we may assume
![]() $M=U\to K^n$
is étale. Now if
$M=U\to K^n$
is étale. Now if
![]() $(V_i,\tau _i)$
are charts for N, then
$(V_i,\tau _i)$
are charts for N, then
![]() $f^{-1}\tau _i(V_i)$
cover U, and so the union of their interiors is open dense in U. So we may assume
$f^{-1}\tau _i(V_i)$
cover U, and so the union of their interiors is open dense in U. So we may assume
![]() $N=V\to K^m$
is étale. This case is Lemma 5.6.
$N=V\to K^m$
is étale. This case is Lemma 5.6.
Recall that the local dimension of a definable set X is defined as
Note, in particular, that, in our definition of weak manifolds, the
![]() $U_i$
are étale domains, so that for every
$U_i$
are étale domains, so that for every
![]() $u\in U_i$
there is a definable local homeomorphism of
$u\in U_i$
there is a definable local homeomorphism of
![]() $U_i$
at u with an open subset of
$U_i$
at u with an open subset of
![]() $K^n$
. In particular, the local dimension of each
$K^n$
. In particular, the local dimension of each
![]() $U_i$
, and therefore also of M, is n at every point.
$U_i$
, and therefore also of M, is n at every point.
The next lemma is standard:
Lemma 5.8. Suppose M is a definable topological weak manifold. Let
![]() $X\subset M$
be a definable subset. Then
$X\subset M$
be a definable subset. Then
![]() $\dim (X)=\max _{x\in X}\dim _{x}(X)$
.
$\dim (X)=\max _{x\in X}\dim _{x}(X)$
.
If G is a definable weak topological group and H is a subgroup, then the dimension of H is the local dimension of H at any point.
Proof. If
![]() $M=U_1\cup \cdots \cup U_n$
is a covering by open sets and
$M=U_1\cup \cdots \cup U_n$
is a covering by open sets and
![]() $\varphi _i:U_i\to V_i$
is a homeomorphism onto a set
$\varphi _i:U_i\to V_i$
is a homeomorphism onto a set
![]() $V_i$
, with an étale map
$V_i$
, with an étale map
![]() $V_i\to K^n$
, then
$V_i\to K^n$
, then
![]() $\mathrm {dim}(X)=\max _i(\mathrm {dim }(\varphi _i(X\cap U_i)))$
, and the local dimension of X at
$\mathrm {dim}(X)=\max _i(\mathrm {dim }(\varphi _i(X\cap U_i)))$
, and the local dimension of X at
![]() $x\in X\cap U_i$
is the local dimension of
$x\in X\cap U_i$
is the local dimension of
![]() $\varphi _i(X\cap U_i)$
at
$\varphi _i(X\cap U_i)$
at
![]() $\varphi _i(x)$
, so we reduce to the case
$\varphi _i(x)$
, so we reduce to the case
![]() $M=V$
is étale over
$M=V$
is étale over
![]() $K^n$
. In fact, the result is true whenever
$K^n$
. In fact, the result is true whenever
![]() $M\subset K^m$
with the subspace topology, as then the local dimension of
$M\subset K^m$
with the subspace topology, as then the local dimension of
![]() $X\subset M$
at a point x equals the local dimension of X at x in
$X\subset M$
at a point x equals the local dimension of X at x in
![]() $K^m$
, and so the result follows from Proposition 2.11(3).
$K^m$
, and so the result follows from Proposition 2.11(3).
If G is a definable weak topological group and H is a subgroup, then the local dimension of H at any point
![]() $h\in H$
is constant independent of h. Indeed, the left translation
$h\in H$
is constant independent of h. Indeed, the left translation
![]() ${L_h:G\to G}$
is a definable homeomorphism that sends e to h and satisfies
${L_h:G\to G}$
is a definable homeomorphism that sends e to h and satisfies
![]() $L_h(H)=H$
, so
$L_h(H)=H$
, so
![]() $\mathrm {dim}_e(H)=\mathrm {dim}_h(H)$
.
$\mathrm {dim}_e(H)=\mathrm {dim}_h(H)$
.
Proposition 5.9. Suppose
![]() $T\subset K^m$
is such that there is a coordinate projection
$T\subset K^m$
is such that there is a coordinate projection
![]() $\pi :T\to U$
onto an open subset
$\pi :T\to U$
onto an open subset
![]() $U\subset K^n$
and such that the fibres of
$U\subset K^n$
and such that the fibres of
![]() $\pi $
are finite of constant cardinality, s. Assume that the associated map
$\pi $
are finite of constant cardinality, s. Assume that the associated map
![]() $f:U\to (K^{m-n})^{[s]}$
is continuous. Then
$f:U\to (K^{m-n})^{[s]}$
is continuous. Then
![]() $T\to K^n$
is étale.
$T\to K^n$
is étale.
Proof. Let
![]() $x\in T$
. Replacing U by a smaller neighborhood around
$x\in T$
. Replacing U by a smaller neighborhood around
![]() $\pi (x)$
, we may assume, using Fact 2.13, that f lifts to a continuous function
$\pi (x)$
, we may assume, using Fact 2.13, that f lifts to a continuous function
![]() $g:U\to (K^{m-n})^s$
,
$g:U\to (K^{m-n})^s$
,
![]() $g=(g_1,\cdots ,g_s)$
. In this case, one gets that T is homeomorphic to
$g=(g_1,\cdots ,g_s)$
. In this case, one gets that T is homeomorphic to
![]() $\bigsqcup _{i=1}^sU$
over U, via the map
$\bigsqcup _{i=1}^sU$
over U, via the map
![]() ${(a,i)\mapsto (a,g_i(a))}$
.
${(a,i)\mapsto (a,g_i(a))}$
.
Lemma 5.10. Suppose
![]() $M=\bigcup _{i=1}^r\varphi _i(U_i)$
, where
$M=\bigcup _{i=1}^r\varphi _i(U_i)$
, where
![]() $\varphi _i:U_i\to M$
are injective definable functions, such that the
$\varphi _i:U_i\to M$
are injective definable functions, such that the
![]() $U_i$
are definable (weak)
$U_i$
are definable (weak)
![]() $\mathcal {P}$
-n-manifolds. Suppose further that for all
$\mathcal {P}$
-n-manifolds. Suppose further that for all
![]() $i,j$
, the sets
$i,j$
, the sets
![]() $U_{ij}:=\varphi _i^{-1}(\varphi _j(U_j))$
are open in
$U_{ij}:=\varphi _i^{-1}(\varphi _j(U_j))$
are open in
![]() $U_i$
, and the transition maps
$U_i$
, and the transition maps
![]() $U_{ij}\to U_{ji}$
given by
$U_{ij}\to U_{ji}$
given by
![]() $x\mapsto \varphi _j^{-1}\varphi _i(x)$
are
$x\mapsto \varphi _j^{-1}\varphi _i(x)$
are
![]() $\mathcal {P}$
-maps. Then M has a unique (up to isomorphism) structure of a definable (weak)
$\mathcal {P}$
-maps. Then M has a unique (up to isomorphism) structure of a definable (weak)
![]() $\mathcal {P}$
-n-manifold such that
$\mathcal {P}$
-n-manifold such that
![]() $\varphi _i:U_i\to M$
is an open immersion.
$\varphi _i:U_i\to M$
is an open immersion.
The proof is straightforward and omitted.
Proposition 5.11. Suppose M is a definable weak topological manifold. Then
![]() $X\subset M$
is large (i.e.,
$X\subset M$
is large (i.e.,
![]() $\dim (M\setminus X)<\dim (M)$
) if and only if the interior of X in M is dense in M.
$\dim (M\setminus X)<\dim (M)$
) if and only if the interior of X in M is dense in M.
Proof. Because the dimension of
![]() $M\setminus X$
is the maximum of the local dimension at its points by Lemma 5.8, we conclude that both conditions are local, and so we may assume
$M\setminus X$
is the maximum of the local dimension at its points by Lemma 5.8, we conclude that both conditions are local, and so we may assume
![]() $M=U\subset K^n$
is open. Here, the result follows from dimension theory.
$M=U\subset K^n$
is open. Here, the result follows from dimension theory.
Proposition 5.12. Suppose M is a weak definable topological manifold and
![]() $X\subset M$
is definable. Then X is a finite union of locally closed definable subsets of M.
$X\subset M$
is definable. Then X is a finite union of locally closed definable subsets of M.
Proof. There is an immediate reduction to the case where
![]() $M=U\to K^n$
is étale. In this case, U has the subspace topology
$M=U\to K^n$
is étale. In this case, U has the subspace topology
![]() $U\subset K^s$
for some s. So it is enough to prove this for
$U\subset K^s$
for some s. So it is enough to prove this for
![]() $X\subset K^s$
. This is a consequence of Proposition 2.17.
$X\subset K^s$
. This is a consequence of Proposition 2.17.
In case
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, a weak manifold is generically a manifold:
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, a weak manifold is generically a manifold:
Proposition 5.13. Suppose
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
. If M is a definable weak
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
. If M is a definable weak
![]() $\mathcal {P}$
-manifold, then there is a definable open dense subset
$\mathcal {P}$
-manifold, then there is a definable open dense subset
![]() $U\subset M$
which is a definable
$U\subset M$
which is a definable
![]() $\mathcal {P}$
-manifold.
$\mathcal {P}$
-manifold.
Proof. There is an immediate reduction to the case in which
![]() $i:M=U\to K^n$
is étale. Let r be a uniform bound on the cardinality of the fibers of i. Denote
$i:M=U\to K^n$
is étale. Let r be a uniform bound on the cardinality of the fibers of i. Denote
![]() $X_s:=\{x\in K^n: \#(i^{-1}(x)) =s\}$
. Letting
$X_s:=\{x\in K^n: \#(i^{-1}(x)) =s\}$
. Letting
![]() $U_s\subset X_k$
be the interior of
$U_s\subset X_k$
be the interior of
![]() $X_s$
, we see that
$X_s$
, we see that
![]() $\bigcup _{s\leq r} U_s$
is open, dense in
$\bigcup _{s\leq r} U_s$
is open, dense in
![]() $K^n$
. Replacing U with
$K^n$
. Replacing U with
![]() $i^{-1}(U_s)$
, we may assume that the nonempty fibers of i have constant cardinality. From the assumption that
$i^{-1}(U_s)$
, we may assume that the nonempty fibers of i have constant cardinality. From the assumption that
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, we conclude that the map
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, we conclude that the map
![]() $i(U)\to (K^r)^{[s]}$
lifts to a definable map
$i(U)\to (K^r)^{[s]}$
lifts to a definable map
![]() $i(U)\to (K^r)^s$
. There is an open dense subset
$i(U)\to (K^r)^s$
. There is an open dense subset
![]() $V'\subset i(U)$
such that
$V'\subset i(U)$
such that
![]() $V'\to i(U)\to (K^r)^s$
is a
$V'\to i(U)\to (K^r)^s$
is a
![]() $\mathcal {P}$
-map (see Proposition 5.6), and we conclude that
$\mathcal {P}$
-map (see Proposition 5.6), and we conclude that
![]() $i^{-1}(V')\cong \bigsqcup _{i=1}^sV'$
over
$i^{-1}(V')\cong \bigsqcup _{i=1}^sV'$
over
![]() $V'$
, which is clearly a
$V'$
, which is clearly a
![]() $\mathcal {P}$
-manifold.
$\mathcal {P}$
-manifold.
It seems possible that in this situation, a weak manifold is already a manifold, but as this is not needed for the sequel, we have not looked into it.
The next couple of results are not used in the main theorems but may be of independent interest. We recall some standard definitions:
Definition 5.14. Suppose M and N are definable strictly differentiable weak manifolds, and
![]() $f:M\to N$
a definable strictly differentiable function.
$f:M\to N$
a definable strictly differentiable function.
Then f is called an immersion if the derivative
![]() $f'(x)$
is injective at all points
$f'(x)$
is injective at all points
![]() $x\in M$
.
$x\in M$
.
f is called an embedding if f is an immersion and a homeomorphism onto its image.
f is called a submersion if the derivative
![]() $f'(x)$
is surjective for all
$f'(x)$
is surjective for all
![]() $x\in M$
.
$x\in M$
.
These notions have the expected properties.
Proposition 5.15. Suppose
![]() $f:M\to N$
is a strictly differentiable definable map of definable strictly differentiable weak manifolds. If f is an immersion, then M satisfies the following universal property: For every definable strictly differentiable weak manifold P, and
$f:M\to N$
is a strictly differentiable definable map of definable strictly differentiable weak manifolds. If f is an immersion, then M satisfies the following universal property: For every definable strictly differentiable weak manifold P, and
![]() $g:P\to M$
, the function g is strictly differentiable and definable if and only if
$g:P\to M$
, the function g is strictly differentiable and definable if and only if
![]() $fg$
is strictly differentiable and g is definable and continuous.
$fg$
is strictly differentiable and g is definable and continuous.
If f is an embedding and
![]() $g:P\to M$
is a function, then g is a strictly differentiable definable map if and only if
$g:P\to M$
is a function, then g is a strictly differentiable definable map if and only if
![]() $fg$
is a strictly differentiable definable map.
$fg$
is a strictly differentiable definable map.
Proposition 5.16. If
![]() $f:M\to N$
is a surjective submersion, then a map
$f:M\to N$
is a surjective submersion, then a map
![]() $g:N\to K$
is a strictly differentiable definable function if and only if the composition
$g:N\to K$
is a strictly differentiable definable function if and only if the composition
![]() $gf$
is strictly differentiable and definable.
$gf$
is strictly differentiable and definable.
These two properties are a consequence of the theorems on the local structure of immersions and submersions, Propositions 4.9 and 4.10. We leave the details for the interested reader to fill.
Suppose M is a definable strictly differentiable weak manifold. If
![]() $M\to N$
is a surjective map of sets, it determines at most one structure of a definable strictly differentiable weak manifold on N in such a way that
$M\to N$
is a surjective map of sets, it determines at most one structure of a definable strictly differentiable weak manifold on N in such a way that
![]() $M\to N$
is a submersion. Also, an injective map
$M\to N$
is a submersion. Also, an injective map
![]() $N\to M$
determines at most one structure of a strictly differentiable weak manifold on N in such a way that
$N\to M$
determines at most one structure of a strictly differentiable weak manifold on N in such a way that
![]() $N\to M$
is an embedding. The subsets
$N\to M$
is an embedding. The subsets
![]() $N\subset M$
admitting such a structure are called submanifolds of M. We also get that if N is a definable topological space, and
$N\subset M$
admitting such a structure are called submanifolds of M. We also get that if N is a definable topological space, and
![]() $N\to M$
is a definable and continuous function, then there is at most one structure of a strictly differentiable definable manifold on N extending the given topology (and the definable structure), and for which
$N\to M$
is a definable and continuous function, then there is at most one structure of a strictly differentiable definable manifold on N extending the given topology (and the definable structure), and for which
![]() $N\to M$
is an immersion. In other words, the strictly differentiable weak manifold structure that makes
$N\to M$
is an immersion. In other words, the strictly differentiable weak manifold structure that makes
![]() $N\to M$
an embedding is determined by the set N, and the strictly differentiable weak manifold structure that makes
$N\to M$
an embedding is determined by the set N, and the strictly differentiable weak manifold structure that makes
![]() $N\to M$
an immersion is determined by the topological space, and definable set N.
$N\to M$
an immersion is determined by the topological space, and definable set N.
Proposition 5.17. Suppose
![]() $M,N$
are definable strictly differentiable weak manifolds, and let
$M,N$
are definable strictly differentiable weak manifolds, and let
![]() $f:M\to N$
be an injective definable map. Then there is a definable open dense subset
$f:M\to N$
be an injective definable map. Then there is a definable open dense subset
![]() $U\subset M$
such that
$U\subset M$
such that
![]() $f|_U$
is an immersion.
$f|_U$
is an immersion.
Proof. By Proposition 5.7 we may assume f is strictly differentiable. We have to show that the interior of the set
![]() $\{x\in M: f'(x) \text { is injective} \}$
is dense in M. If this is not the case, we can find an open nonempty subset of M such that f is not an immersion at any point.
$\{x\in M: f'(x) \text { is injective} \}$
is dense in M. If this is not the case, we can find an open nonempty subset of M such that f is not an immersion at any point.
So suppose M is an open subset of
![]() $K^n$
, N is an open subset of
$K^n$
, N is an open subset of
![]() $K^m$
and f is not an immersion at any point. For dimension reasons,
$K^m$
and f is not an immersion at any point. For dimension reasons,
![]() $n\leq m$
. If we define
$n\leq m$
. If we define
![]() $X_k$
to be the set of points x of M such that
$X_k$
to be the set of points x of M such that
![]() $f'(x)$
is of rank k, then
$f'(x)$
is of rank k, then
![]() $X_0\cup \dots \cup X_{n-1}=M$
, and so if
$X_0\cup \dots \cup X_{n-1}=M$
, and so if
![]() $U_r$
is the interior of
$U_r$
is the interior of
![]() $X_r$
we have that
$X_r$
we have that
![]() $U_1\cup \cdots \cup U_{n-1}$
is open dense in M. So we may assume that f is of constant rank. This contradicts the result in Proposition 4.11 since the map
$U_1\cup \cdots \cup U_{n-1}$
is open dense in M. So we may assume that f is of constant rank. This contradicts the result in Proposition 4.11 since the map
![]() $(x,y)\mapsto (x,0)$
is not injective.
$(x,y)\mapsto (x,0)$
is not injective.
The following facts are standard and are probably known:
Fact 5.18. Suppose X is a Hausdorff space and
![]() $X\to Y$
is a surjective local homeomorphism with fibers of constant cardinality s. Then the map
$X\to Y$
is a surjective local homeomorphism with fibers of constant cardinality s. Then the map
![]() $t:Y\to X^{[s]}$
given by the fibers of p is continuous.
$t:Y\to X^{[s]}$
given by the fibers of p is continuous.
Proof. Let
![]() $\pi :X^{s}\setminus \Delta \to X^{[s]}$
be the canonical projection. Take
$\pi :X^{s}\setminus \Delta \to X^{[s]}$
be the canonical projection. Take
![]() $y\in Y$
and
$y\in Y$
and
![]() $\{x_1,\dots ,x_s\}=p^{-1}(y)=t(y)$
. A basic open neighborhood of
$\{x_1,\dots ,x_s\}=p^{-1}(y)=t(y)$
. A basic open neighborhood of
![]() $t(y)$
is of the form
$t(y)$
is of the form
![]() $\pi (U_1\times \dots \times U_s)$
for
$\pi (U_1\times \dots \times U_s)$
for
![]() $U_k\ni x_k$
open and
$U_k\ni x_k$
open and
![]() $U_k$
pairwise disjoint. Shrinking
$U_k$
pairwise disjoint. Shrinking
![]() $U_k$
, we may assume
$U_k$
, we may assume
![]() $p|_{U_k}$
is a homeomorphism onto an open set. If
$p|_{U_k}$
is a homeomorphism onto an open set. If
![]() $V=\bigcap _kp(U_k)$
, then
$V=\bigcap _kp(U_k)$
, then
![]() $t^{-1}(V)\subset \pi (U_1\times \dots \times U_s)$
.
$t^{-1}(V)\subset \pi (U_1\times \dots \times U_s)$
.
Fact 5.19. Let
![]() $X,Y,Z$
be topological spaces,
$X,Y,Z$
be topological spaces,
![]() $p:X\to Z$
,
$p:X\to Z$
,
![]() $q:Y\to Z$
be surjective continuous functions and
$q:Y\to Z$
be surjective continuous functions and
![]() $f:X\to Y$
be a continuous bijection such that
$f:X\to Y$
be a continuous bijection such that
![]() $qf=p$
. Assume that X and Y are Hausdorff spaces and
$qf=p$
. Assume that X and Y are Hausdorff spaces and
![]() $p:X\to Z$
has finite fibers of constant cardinality, s. If the map
$p:X\to Z$
has finite fibers of constant cardinality, s. If the map
![]() $t:Z\to X^{[s]}$
given by
$t:Z\to X^{[s]}$
given by
![]() $z\mapsto p^{-1}(z)$
is continuous, then f is a homeomorphism.
$z\mapsto p^{-1}(z)$
is continuous, then f is a homeomorphism.
Proof. Since f is continuous and bijective, we only need to show that it is open, which is a local property. Fix some
![]() $x\in X$
and
$x\in X$
and
![]() $z=p(x)$
. By Fact 2.13, the map
$z=p(x)$
. By Fact 2.13, the map
![]() $Z\to X^{[s]}$
lifts, locally near z, to a continuous map
$Z\to X^{[s]}$
lifts, locally near z, to a continuous map
![]() $(l_1,\dots , l_s):Z\to X^s$
. Shrinking Z to this neighborhood, and reducing X and Y accordingly, we may assume that X is homeomorphic to
$(l_1,\dots , l_s):Z\to X^s$
. Shrinking Z to this neighborhood, and reducing X and Y accordingly, we may assume that X is homeomorphic to
![]() $\bigsqcup _{i\leq s}Z$
over Z, via the homeomorphism
$\bigsqcup _{i\leq s}Z$
over Z, via the homeomorphism
![]() $F_l:\bigsqcup _{i\leq s}Z\to X$
, given by
$F_l:\bigsqcup _{i\leq s}Z\to X$
, given by
![]() $(i,z)\mapsto l_i(z)$
. To see that this is a homeomorphism, note that the image of the i-th-cofactor via
$(i,z)\mapsto l_i(z)$
. To see that this is a homeomorphism, note that the image of the i-th-cofactor via
![]() $F_l$
is the set
$F_l$
is the set
![]() $X_i=\{x\in X\mid x=l_ip(x)\}$
, which is closed in X (because X is Hausdorff). Since there are only finitely many
$X_i=\{x\in X\mid x=l_ip(x)\}$
, which is closed in X (because X is Hausdorff). Since there are only finitely many
![]() $X_i$
(and they are pairwise disjoint), they are also open. Finally, the inverse of
$X_i$
(and they are pairwise disjoint), they are also open. Finally, the inverse of
![]() $F_l$
restricted to
$F_l$
restricted to
![]() $X_i$
coincides with p which is continuous.
$X_i$
coincides with p which is continuous.
Similarly, we have a homeomorphism
![]() $F_{fl}:\bigsqcup _{i\leq s}Z\to Y$
, which is compatible with f in the sense that
$F_{fl}:\bigsqcup _{i\leq s}Z\to Y$
, which is compatible with f in the sense that
![]() $fF_l=F_{fl}$
. We conclude that f is a homeomorphism, as required.
$fF_l=F_{fl}$
. We conclude that f is a homeomorphism, as required.
Proposition 5.20. Let
![]() $M, N$
be strictly differentiable weak manifolds, and
$M, N$
be strictly differentiable weak manifolds, and
![]() $f:M\to N$
be an injective definable function. Then there is a definable dense open
$f:M\to N$
be an injective definable function. Then there is a definable dense open
![]() $U\subset M$
such that
$U\subset M$
such that
![]() $f|_U$
is an embedding.
$f|_U$
is an embedding.
Proof. By Proposition 5.17, we may assume that f is an immersion. If
![]() $V_1,\dots ,V_n$
is a finite open cover of N and the statement is valid for
$V_1,\dots ,V_n$
is a finite open cover of N and the statement is valid for
![]() $f:f^{-1}V_i\to V_i$
, then it is also valid for f. So we may assume
$f:f^{-1}V_i\to V_i$
, then it is also valid for f. So we may assume
![]() $N=V\to K^m$
is étale. From the definition, we have that
$N=V\to K^m$
is étale. From the definition, we have that
![]() $V\subset K^d$
has the subspace topology. Since
$V\subset K^d$
has the subspace topology. Since
![]() $f:M\to V$
is an immersion, to verify that it is an embedding it suffices to show that it is a topological embedding into
$f:M\to V$
is an immersion, to verify that it is an embedding it suffices to show that it is a topological embedding into
![]() $K^d$
. So we may assume
$K^d$
. So we may assume
![]() $N=K^m$
.
$N=K^m$
.
Now consider
![]() $U_1\cup \dots \cup U_n=M$
a finite open cover of M. Assume, first, that
$U_1\cup \dots \cup U_n=M$
a finite open cover of M. Assume, first, that
![]() $f|_{U_i}$
is an embedding. Define
$f|_{U_i}$
is an embedding. Define
![]() $U_i^{\prime }=\text {Int}(U_i\setminus \bigcup _{j<i}U_i)$
, and
$U_i^{\prime }=\text {Int}(U_i\setminus \bigcup _{j<i}U_i)$
, and
![]() $U_i^{\prime \prime }=U_i^{\prime }\setminus \bigcup _{j\neq i}f^{-1}\operatorname {\mathrm {cl}}(f(U_j^{\prime }))$
. Note that
$U_i^{\prime \prime }=U_i^{\prime }\setminus \bigcup _{j\neq i}f^{-1}\operatorname {\mathrm {cl}}(f(U_j^{\prime }))$
. Note that
![]() $\bigcup _i U_i^{\prime }\subset M$
is an open dense set. Also, note that
$\bigcup _i U_i^{\prime }\subset M$
is an open dense set. Also, note that
![]() $f(U_i^{\prime }\setminus U_i^{\prime \prime })= \bigcup _{j\neq i}f(U_i^{\prime }) \cap \operatorname {\mathrm {cl}}(f(U_j^{\prime }))\subset \bigcup _{j\neq i}\operatorname {\mathrm {cl}}(f(U_j^{\prime }))\setminus f(U_j^{\prime })$
. So we conclude that
$f(U_i^{\prime }\setminus U_i^{\prime \prime })= \bigcup _{j\neq i}f(U_i^{\prime }) \cap \operatorname {\mathrm {cl}}(f(U_j^{\prime }))\subset \bigcup _{j\neq i}\operatorname {\mathrm {cl}}(f(U_j^{\prime }))\setminus f(U_j^{\prime })$
. So we conclude that
![]() $\dim (U_i^{\prime }\setminus U_i^{\prime \prime })<\dim (M)$
, by Proposition 2.18. Thus, replacing
$\dim (U_i^{\prime }\setminus U_i^{\prime \prime })<\dim (M)$
, by Proposition 2.18. Thus, replacing
![]() $U_i$
with
$U_i$
with
![]() $U_i^{\prime \prime }$
, we may assume
$U_i^{\prime \prime }$
, we may assume
![]() $\operatorname {\mathrm {cl}} (f(U_i))\cap f(U_j)=\emptyset $
for distinct
$\operatorname {\mathrm {cl}} (f(U_i))\cap f(U_j)=\emptyset $
for distinct
![]() $i,j$
. In this case, one verifies that f is a topological embedding.
$i,j$
. In this case, one verifies that f is a topological embedding.
We are thus reduced to the case where
![]() $M=U\to K^n$
is étale.
$M=U\to K^n$
is étale.
Consider for each
![]() $I\subset \{1,\dots ,m\}$
of size n, the set
$I\subset \{1,\dots ,m\}$
of size n, the set
![]() $A_I$
of
$A_I$
of
![]() $x\in U$
such that the I-th-minor of
$x\in U$
such that the I-th-minor of
![]() $f'(x)$
is invertible. As
$f'(x)$
is invertible. As
![]() $U=\bigcup _IA_I$
, we conclude that
$U=\bigcup _IA_I$
, we conclude that
![]() $U'=\bigcup _I\text {Int}(A_I)$
is open dense in U, so by the reduction in the previous paragraph, we may assume that the composition of
$U'=\bigcup _I\text {Int}(A_I)$
is open dense in U, so by the reduction in the previous paragraph, we may assume that the composition of
![]() $f:U\to K^m$
with the projection onto the first n coordinates
$f:U\to K^m$
with the projection onto the first n coordinates
![]() $p:K^m\to K^n$
is an étale immersion. If s is a uniform bound for the size of the fibers of U over
$p:K^m\to K^n$
is an étale immersion. If s is a uniform bound for the size of the fibers of U over
![]() $K^n$
, then we can take
$K^n$
, then we can take
![]() $A_k$
the set of
$A_k$
the set of
![]() $x\in K^m$
such that the fiber
$x\in K^m$
such that the fiber
![]() $(pf)^{-1}(x)$
has k elements and consider
$(pf)^{-1}(x)$
has k elements and consider
![]() $U'=\bigcup _{k\leq s}\text {Int}(A_k)$
. So we may assume that if
$U'=\bigcup _{k\leq s}\text {Int}(A_k)$
. So we may assume that if
![]() $V=pf(U)$
, the fibers of
$V=pf(U)$
, the fibers of
![]() $pf:U\to V$
have the same size s.
$pf:U\to V$
have the same size s.
In this case, the function
![]() $V\to U^{[s]}$
, given by
$V\to U^{[s]}$
, given by
![]() $x\mapsto (pf)^{-1}(x)$
, is continuous, and the function f is a topological homeomorphism
$x\mapsto (pf)^{-1}(x)$
, is continuous, and the function f is a topological homeomorphism
![]() $U\to f(U)$
; see facts 5.18 and 5.19.
$U\to f(U)$
; see facts 5.18 and 5.19.
We can now prove a
![]() $1$
-h-minimal version of Sard’s Lemma (compare with [Reference Wilkie16, Theorem 2.7] for an analogous result in the o-minimal setting). Namely, given a definable strictly differentiable morphism, f, of definable weak manifolds, call a value x of f regular when f is a submersion at every point of
$1$
-h-minimal version of Sard’s Lemma (compare with [Reference Wilkie16, Theorem 2.7] for an analogous result in the o-minimal setting). Namely, given a definable strictly differentiable morphism, f, of definable weak manifolds, call a value x of f regular when f is a submersion at every point of
![]() $f^{-1}(x)$
. The statement is, then, that the set of singular values is small:
$f^{-1}(x)$
. The statement is, then, that the set of singular values is small:
Proposition 5.21. Suppose M and N are definable strictly differentiable weak manifolds. If
![]() $f:M\to N$
is a strictly differentiable map, then there exists an open dense subset
$f:M\to N$
is a strictly differentiable map, then there exists an open dense subset
![]() $U\subset N$
such that
$U\subset N$
such that
![]() $f:f^{-1}(U)\to U$
is a submersion.
$f:f^{-1}(U)\to U$
is a submersion.
Proof. We have to see that the image via f of the set of points
![]() $x\in M$
such that
$x\in M$
such that
![]() $f'(x)$
is not surjective, and is nowhere dense in N. This property is expressible by a first order formula, so we may assume that
$f'(x)$
is not surjective, and is nowhere dense in N. This property is expressible by a first order formula, so we may assume that
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
; see Fact 2.5 and the subsequent remark.
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
; see Fact 2.5 and the subsequent remark.
Let
![]() $m=\dim (N)$
. Let
$m=\dim (N)$
. Let
![]() $X\subset M$
be a definable set such that for all
$X\subset M$
be a definable set such that for all
![]() $x\in X$
,
$x\in X$
,
![]() $f'(x)$
is not surjective. We have to see that
$f'(x)$
is not surjective. We have to see that
![]() $\dim f(X)<m$
. We do this by induction on the dimension of X. The base case, when X is finite, is trivial.
$\dim f(X)<m$
. We do this by induction on the dimension of X. The base case, when X is finite, is trivial.
The dimension of
![]() $f(X)$
is the maximum of the local dimensions at points; see Proposition 5.8. So we may assume
$f(X)$
is the maximum of the local dimensions at points; see Proposition 5.8. So we may assume
![]() $N\subset K^m$
is open. Covering M by a finite number of charts, we may assume
$N\subset K^m$
is open. Covering M by a finite number of charts, we may assume
![]() $M\to K^n$
is étale, say
$M\to K^n$
is étale, say
![]() $M\subset K^r$
.
$M\subset K^r$
.
Then by Proposition 2.15, there exists a finite partition of X into definable sets such that if
![]() $X'$
is an element of the partition, there exists a coordinate projection
$X'$
is an element of the partition, there exists a coordinate projection
![]() $p:K^r\to K^l$
, which restricted to
$p:K^r\to K^l$
, which restricted to
![]() $X'$
is a surjection
$X'$
is a surjection
![]() $X'\to U$
onto an open subset
$X'\to U$
onto an open subset
![]() $U\subset K^l$
with finite fibers of constant cardinality. If we prove that
$U\subset K^l$
with finite fibers of constant cardinality. If we prove that
![]() $\dim f(X')<m$
for every element
$\dim f(X')<m$
for every element
![]() $X'$
of the partition, then also
$X'$
of the partition, then also
![]() $\dim f(X)<m$
. So we may assume there is a coordinate projection
$\dim f(X)<m$
. So we may assume there is a coordinate projection
![]() $p:X\to U$
onto an open subset
$p:X\to U$
onto an open subset
![]() $U\subset K^l$
, such that
$U\subset K^l$
, such that
![]() $p^{-1}(u)$
has t elements for all
$p^{-1}(u)$
has t elements for all
![]() $u\in U$
. From the assumption
$u\in U$
. From the assumption
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, we get that there are definable sections
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, we get that there are definable sections
![]() $s_1,\dots ,s_t:U\to X$
, such that
$s_1,\dots ,s_t:U\to X$
, such that
![]() $\{s_1(u),\cdots ,s_t(u)\}=p^{-1}(u)$
, for all
$\{s_1(u),\cdots ,s_t(u)\}=p^{-1}(u)$
, for all
![]() $u\in U$
. As
$u\in U$
. As
![]() $X=\bigcup _{i\le t}s_i(U)$
, we may assume that
$X=\bigcup _{i\le t}s_i(U)$
, we may assume that
![]() $p:X\to U$
is a bijection with inverse
$p:X\to U$
is a bijection with inverse
![]() $s:U\to X$
. The map
$s:U\to X$
. The map
![]() $s:U\to M$
becomes strictly differentiable in an open dense
$s:U\to M$
becomes strictly differentiable in an open dense
![]() $V\subset U$
; see Proposition 5.7. As
$V\subset U$
; see Proposition 5.7. As
![]() $s(U\setminus V)$
has smaller dimension than X, we may assume that s is strictly differentiable. Now note that s has image in X, and so the composition
$s(U\setminus V)$
has smaller dimension than X, we may assume that s is strictly differentiable. Now note that s has image in X, and so the composition
![]() $U\to M\to N$
has derivative which is not surjective at any point of U. So we have reduced to the case in which
$U\to M\to N$
has derivative which is not surjective at any point of U. So we have reduced to the case in which
![]() $M=U\subset K^n$
is open and
$M=U\subset K^n$
is open and
![]() $X=U$
.
$X=U$
.
If we consider
![]() $A_k\subset U$
, the set defined by
$A_k\subset U$
, the set defined by
![]() $A_k=\{x\in U: f'(x)\text { has rank }k\}$
, then
$A_k=\{x\in U: f'(x)\text { has rank }k\}$
, then
![]() $\bigcup _{k<m}A_k=U$
, and so
$\bigcup _{k<m}A_k=U$
, and so
![]() $\bigcup _{k<m}\text {Int}(A_k)$
is open and dense in U. We conclude by the induction hypothesis that the image of
$\bigcup _{k<m}\text {Int}(A_k)$
is open and dense in U. We conclude by the induction hypothesis that the image of
![]() $U\setminus \bigcup _{k<m}\text {Int}(A_k)$
is nowhere dense in N, and so we may assume that
$U\setminus \bigcup _{k<m}\text {Int}(A_k)$
is nowhere dense in N, and so we may assume that
![]() $f'(x)$
has constant rank k in U, for a
$f'(x)$
has constant rank k in U, for a
![]() $k<m$
.
$k<m$
.
Consider the set
![]() $Y=\{x\in U: \dim f^{-1}f(x)\geq \dim (U)-k\}$
. Then Y is definable because dimension is definable in definable families. Also, Y has dense interior by the constant rank theorem, Proposition 4.11. So once more by the induction hypothesis, we may assume
$Y=\{x\in U: \dim f^{-1}f(x)\geq \dim (U)-k\}$
. Then Y is definable because dimension is definable in definable families. Also, Y has dense interior by the constant rank theorem, Proposition 4.11. So once more by the induction hypothesis, we may assume
![]() $f^{-1}f(x)$
has dimension at least
$f^{-1}f(x)$
has dimension at least
![]() $\dim (U)-k$
for all
$\dim (U)-k$
for all
![]() $x\in U$
. Then the dimension of
$x\in U$
. Then the dimension of
![]() $f(U)$
is at most k, by the additivity of dimension.
$f(U)$
is at most k, by the additivity of dimension.
If
![]() $M\to N$
is a map of strictly differentiable weak manifolds, and
$M\to N$
is a map of strictly differentiable weak manifolds, and
![]() $y\in N$
is a regular value, then one can show
$y\in N$
is a regular value, then one can show
![]() $f^{-1}(y)\subset M$
is a strictly differentiable weak submanifold.
$f^{-1}(y)\subset M$
is a strictly differentiable weak submanifold.
6. Definable Lie groups
In this section, we show that every definable group is a definable weak Lie group and that the germ of a definable weak Lie group morphism is determined by its derivative at the identity.
The proof of the following lemma was communicated to us by Martin Hils.
Lemma 6.1. Suppose G is a group a-definable in a pregeometric theory, and that
![]() ${X,Y\subset G}$
are nonempty a-definable sets of dimension smaller than
${X,Y\subset G}$
are nonempty a-definable sets of dimension smaller than
![]() $\dim (G)$
. If
$\dim (G)$
. If
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $\dim (gX\cap Y)=\dim (X)$
, then
$\dim (gX\cap Y)=\dim (X)$
, then
![]() $\dim (g/a)\leq \dim (Y)$
.
$\dim (g/a)\leq \dim (Y)$
.
In particular, there exists
![]() $g\in G$
such that
$g\in G$
such that
![]() $\dim (gX\cap Y)<\dim (X)$
.
$\dim (gX\cap Y)<\dim (X)$
.
Proof. Denote
![]() $d=\dim (X)$
and
$d=\dim (X)$
and
![]() $d'=\dim (Y)$
. Suppose
$d'=\dim (Y)$
. Suppose
![]() $\dim (gX\cap Y)=d$
. Note that
$\dim (gX\cap Y)=d$
. Note that
![]() $d\leq d'$
. Let
$d\leq d'$
. Let
![]() $h'\in gX\cap Y$
be such that
$h'\in gX\cap Y$
be such that
![]() $\dim (h'/ag)=d$
. Let
$\dim (h'/ag)=d$
. Let
![]() $h=g^{-1}h'$
.
$h=g^{-1}h'$
.
As
![]() $h\in X$
, we have
$h\in X$
, we have
![]() $d\geq \dim (h/a)\geq \dim (h/ag)=\dim (h'/ag)=d$
. The first inequality is because
$d\geq \dim (h/a)\geq \dim (h/ag)=\dim (h'/ag)=d$
. The first inequality is because
![]() $h\in X$
, the third one because h and
$h\in X$
, the third one because h and
![]() $h'$
are inter-definable over
$h'$
are inter-definable over
![]() $ag$
, and the fourth one by choice of
$ag$
, and the fourth one by choice of
![]() $h'$
. We conclude that h and g are algebraically independent over a.
$h'$
. We conclude that h and g are algebraically independent over a.
Then we obtain that
![]() $d'\geq \dim (h'/a)\geq \dim (h'/ah)=\dim (g/ah)=\dim (g/a)$
. The first inequality because
$d'\geq \dim (h'/a)\geq \dim (h'/ah)=\dim (g/ah)=\dim (g/a)$
. The first inequality because
![]() $h'\in Y$
, the third equality because
$h'\in Y$
, the third equality because
![]() $h'$
and g are inter-definable over
$h'$
and g are inter-definable over
![]() $ah$
, and the fourth equality because h and g are algebraically independent over a.
$ah$
, and the fourth equality because h and g are algebraically independent over a.
For the second statement, note that if
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $\dim (g/a)=\dim (G)$
, or more generally
$\dim (g/a)=\dim (G)$
, or more generally
![]() $\dim (g/a)>d'$
, then by what we have just shown,
$\dim (g/a)>d'$
, then by what we have just shown,
![]() $\dim (gX\cap Y)<\dim (Y)$
.
$\dim (gX\cap Y)<\dim (Y)$
.
The next lemma generalises Lemma 2.4 of [Reference Pillay11] for o-minimal theories. Pillay’s proof can be seen to generalise, with some effort, to geometric theories. We give a different proof:
Lemma 6.2. Suppose G is a group definable in a pregeometric theory and
![]() $X\subset G$
is large (i.e.,
$X\subset G$
is large (i.e.,
![]() $\dim (G\setminus X)<\dim (G)$
). Then a finite number of translates of X cover G.
$\dim (G\setminus X)<\dim (G)$
). Then a finite number of translates of X cover G.
Proof. Suppose we have
![]() $g_0,\cdots ,g_n\in G$
such that
$g_0,\cdots ,g_n\in G$
such that
![]() $\dim (G\setminus (\bigcup _k g_kX))=m$
. By Lemma 6.1 applied to
$\dim (G\setminus (\bigcup _k g_kX))=m$
. By Lemma 6.1 applied to
![]() $G\setminus X$
and
$G\setminus X$
and
![]() $G\setminus (\bigcup _kg_kX)$
, we get that there is
$G\setminus (\bigcup _kg_kX)$
, we get that there is
![]() $g_{n+1}\in G$
such that
$g_{n+1}\in G$
such that
![]() $\dim (G\setminus \bigcup _{k\leq (n+1)}g_kX)<m$
, which – within at most m iterations – finishes the proof.
$\dim (G\setminus \bigcup _{k\leq (n+1)}g_kX)<m$
, which – within at most m iterations – finishes the proof.
Lemma 6.3. Suppose G is a definable group in a pregeometric theory and
![]() $V\subset G$
is large. Then every
$V\subset G$
is large. Then every
![]() $g\in G$
is a product of two elements in V.
$g\in G$
is a product of two elements in V.
Proof. The proof of [Reference Pillay11, Lemma 2.1] works: if we take
![]() $h\in G$
generic over g, then
$h\in G$
generic over g, then
![]() $h^{-1}g$
is also generic over g, and so
$h^{-1}g$
is also generic over g, and so
![]() $h,h^{-1}g\in V$
and their product is g.
$h,h^{-1}g\in V$
and their product is g.
Proposition 6.4. A definable group can be given the structure of a definable strictly differentiable weak
![]() $T_k$
-Lie group. The forgetful functor from definable strictly differentiable weak Lie groups to definable groups is an equivalence of categories.
$T_k$
-Lie group. The forgetful functor from definable strictly differentiable weak Lie groups to definable groups is an equivalence of categories.
If
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, the forgetful functor from definable strictly differentiable
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, the forgetful functor from definable strictly differentiable
![]() $T_k$
-Lie groups to definable groups is an equivalence of categories.
$T_k$
-Lie groups to definable groups is an equivalence of categories.
Proof. That the forgetful functor is full follows from Proposition 5.7. Indeed, suppose G and H are strictly differentiable or
![]() $T_k$
-Lie groups, and let
$T_k$
-Lie groups, and let
![]() $f:G\to H$
be a definable group morphism. Then by Proposition 5.7, there is an open dense
$f:G\to H$
be a definable group morphism. Then by Proposition 5.7, there is an open dense
![]() $U\subset G$
such that
$U\subset G$
such that
![]() $f:U\to H$
is strictly differentiable or
$f:U\to H$
is strictly differentiable or
![]() $T_k$
. If
$T_k$
. If
![]() $g_0\in U$
is arbitrary, and
$g_0\in U$
is arbitrary, and
![]() $g\in G$
, consider the formula
$g\in G$
, consider the formula
![]() $f=L_{f(g)f(g_0)^{-1}}fL_{g_0g^{-1}}$
, where we are denoting
$f=L_{f(g)f(g_0)^{-1}}fL_{g_0g^{-1}}$
, where we are denoting
![]() $L_h$
the left translate by h. Now,
$L_h$
the left translate by h. Now,
![]() $L_{g_0g^{-1}}$
is a strict diffeomorphism or
$L_{g_0g^{-1}}$
is a strict diffeomorphism or
![]() $T_k$
-isomorphism which sends g to
$T_k$
-isomorphism which sends g to
![]() $g_0$
, and
$g_0$
, and
![]() $L_{f(g)f(g_0)^{-1}}$
is a strict diffeomorphism or
$L_{f(g)f(g_0)^{-1}}$
is a strict diffeomorphism or
![]() $T_k$
-isomorphism. We conclude that f being strictly differentiable or
$T_k$
-isomorphism. We conclude that f being strictly differentiable or
![]() $T_k$
at
$T_k$
at
![]() $g_0$
implies that f is strictly differentiable of
$g_0$
implies that f is strictly differentiable of
![]() $T_k$
at g.
$T_k$
at g.
To see that the forgetful functor is essentially surjective, one follows the proof of [Reference Pillay11, Proposition 2.5]. Namely, let G be of dimension n. Decompose G as in Proposition 2.15, and let
![]() $V_0\subset G$
be the union of the n-dimensional pieces
$V_0\subset G$
be the union of the n-dimensional pieces
![]() $U_0,\cdots , U_r$
. Give
$U_0,\cdots , U_r$
. Give
![]() $V_0$
the structure of a weak strictly differentiable manifold with charts the inclusions
$V_0$
the structure of a weak strictly differentiable manifold with charts the inclusions
![]() $U_i\to V_0$
; see Proposition 5.9.
$U_i\to V_0$
; see Proposition 5.9.
Note as an aside that this gives
![]() $V_0$
a topology which might be different from the subspace topology of
$V_0$
a topology which might be different from the subspace topology of
![]() $V_0\subset G\subset K^s$
. In what follows topological notions on
$V_0\subset G\subset K^s$
. In what follows topological notions on
![]() $V_0$
refer to the manifold topology, not this subspace topology. These two topologies coincide in an open dense subset of
$V_0$
refer to the manifold topology, not this subspace topology. These two topologies coincide in an open dense subset of
![]() $V_0$
, by Proposition 5.20, but this is not needed for this proof.
$V_0$
, by Proposition 5.20, but this is not needed for this proof.
Note that
![]() $V_0^{-1}\subset G$
is large in G, as the inverse function is a definable bijection, sending the large subset
$V_0^{-1}\subset G$
is large in G, as the inverse function is a definable bijection, sending the large subset
![]() $V_0$
onto
$V_0$
onto
![]() $V_0^{-1}$
. As the intersection of two large sets is large, we conclude that
$V_0^{-1}$
. As the intersection of two large sets is large, we conclude that
![]() $V_0\cap V_0^{-1}$
is large in G. A fortiori,
$V_0\cap V_0^{-1}$
is large in G. A fortiori,
![]() $V_0\cap V_0^{-1}$
is large in
$V_0\cap V_0^{-1}$
is large in
![]() $V_0$
and so it contains an open dense subset of
$V_0$
and so it contains an open dense subset of
![]() $V_0$
; see Proposition 5.11. Let
$V_0$
; see Proposition 5.11. Let
![]() $V_1\subset V_0\cap V_0^{-1}$
be open dense in
$V_1\subset V_0\cap V_0^{-1}$
be open dense in
![]() $V_0$
such that the inverse function on
$V_0$
such that the inverse function on
![]() $V_1$
(and into
$V_1$
(and into
![]() $V_0$
) is strictly differentiable and
$V_0$
) is strictly differentiable and
![]() $T_k$
; see Proposition 5.7.
$T_k$
; see Proposition 5.7.
Similarly, we have that
![]() $V_0\times V_0\cap m^{-1}(V_0)$
is large in
$V_0\times V_0\cap m^{-1}(V_0)$
is large in
![]() $G\times G$
. Indeed,
$G\times G$
. Indeed,
![]() $m^{-1}(V_0)$
is the inverse image of the large subset
$m^{-1}(V_0)$
is the inverse image of the large subset
![]() $G\times V_0$
of
$G\times V_0$
of
![]() $G\times G$
under the definable bijection
$G\times G$
under the definable bijection
![]() $(\operatorname {\mathrm {Id}},m):G\times G\to G\times G$
. In the same way as before, we find
$(\operatorname {\mathrm {Id}},m):G\times G\to G\times G$
. In the same way as before, we find
![]() $Y_0\subset V_0\times V_0\cap m^{-1}(V_0)$
open and dense in
$Y_0\subset V_0\times V_0\cap m^{-1}(V_0)$
open and dense in
![]() $V_0\times V_0$
such that the multiplication map
$V_0\times V_0$
such that the multiplication map
![]() $Y_0\to V_0$
is strictly differentiable and
$Y_0\to V_0$
is strictly differentiable and
![]() $T_k$
.
$T_k$
.
Now we take
Note that
![]() $V_1^{\prime }$
is definable because
$V_1^{\prime }$
is definable because
![]() $g\in V_1^{\prime }$
is equivalent to
$g\in V_1^{\prime }$
is equivalent to
![]() $\dim (G\setminus X_g)<n$
for
$\dim (G\setminus X_g)<n$
for
![]() $X_g=\{h\in G: (h,g),(h^{-1},hg)\in Y_0\}$
, and dimension is definable in definable families in geometric theories. Note also that
$X_g=\{h\in G: (h,g),(h^{-1},hg)\in Y_0\}$
, and dimension is definable in definable families in geometric theories. Note also that
![]() $V_1^{\prime }$
is large in G because if
$V_1^{\prime }$
is large in G because if
![]() $g\in G$
is generic and
$g\in G$
is generic and
![]() $h\in G$
is generic over g, then
$h\in G$
is generic over g, then
![]() $(h,g)$
is generic in
$(h,g)$
is generic in
![]() $G\times G$
, and
$G\times G$
, and
![]() $(h^{-1},hg)$
, being the image of a definable bijection at
$(h^{-1},hg)$
, being the image of a definable bijection at
![]() $(h,g)$
, is also generic in
$(h,g)$
, is also generic in
![]() $G\times G$
, so they belong to
$G\times G$
, so they belong to
![]() $Y_0$
because
$Y_0$
because
![]() $Y_0$
is large in
$Y_0$
is large in
![]() $G\times G$
.
$G\times G$
.
Now take
![]() $V_2$
the interior of
$V_2$
the interior of
![]() $V_1^{\prime }$
in
$V_1^{\prime }$
in
![]() $V_0$
and
$V_0$
and
![]() $V=V_2\cap V_2^{-1}$
. Then
$V=V_2\cap V_2^{-1}$
. Then
![]() $V_2$
is large in
$V_2$
is large in
![]() $V_0$
by Proposition 5.11, and so it is also large in G. So we conclude that V is an open dense subset of
$V_0$
by Proposition 5.11, and so it is also large in G. So we conclude that V is an open dense subset of
![]() $V_0$
.
$V_0$
.
Define also
![]() $Y=\{(g,h): g,h, gh\in V, (g,h)\in Y_0\}$
. Then Y is open dense in
$Y=\{(g,h): g,h, gh\in V, (g,h)\in Y_0\}$
. Then Y is open dense in
![]() $V_0\times V_0$
. This is because Y is large in
$V_0\times V_0$
. This is because Y is large in
![]() $G\times G$
, with arguments as above, and it is open in
$G\times G$
, with arguments as above, and it is open in
![]() $Y_0$
because multiplication is continuous in
$Y_0$
because multiplication is continuous in
![]() $Y_0$
.
$Y_0$
.
Then we have shown the following:
-
(1) V is large in G.
-
(2) Y is a dense open subset of
 $V\times V$
, and multiplication
$V\times V$
, and multiplication
 $Y\to V$
is strictly differentiable and
$Y\to V$
is strictly differentiable and
 $T_k$
.
$T_k$
. -
(3) Inversion is a strictly differentiable
 $T_k$
-map from V onto V.
$T_k$
-map from V onto V. -
(4) If
 $g\in V$
and
$g\in V$
and
 $h\in G$
is generic in G over g, then
$h\in G$
is generic in G over g, then
 $(h,g),(h^{-1},hg)\in Y$
.
$(h,g),(h^{-1},hg)\in Y$
.
For the last item, note that
![]() $h,hg,h^{-1}\in G$
are generic, and so they belong to V. Also, because
$h,hg,h^{-1}\in G$
are generic, and so they belong to V. Also, because
![]() $g\in V_1^{\prime }$
, one has that
$g\in V_1^{\prime }$
, one has that
![]() $(h,g), (h^{-1},hg)\in Y_0$
.
$(h,g), (h^{-1},hg)\in Y_0$
.
From this, one gets the following:
-
(a) For every
 $g,h\in G$
, the set
$g,h\in G$
, the set
 $Z=\{x\in V: gxh\in V\}$
is open, and
$Z=\{x\in V: gxh\in V\}$
is open, and
 $Z\to V$
given by
$Z\to V$
given by
 $x\mapsto gxh$
is strictly differentiable and
$x\mapsto gxh$
is strictly differentiable and
 $T_k$
.
$T_k$
. -
(b) For every
 $g,h\in G$
, the set
$g,h\in G$
, the set
 $W=\{(x,y)\in V\times V: gxhy\in V\}$
is open in
$W=\{(x,y)\in V\times V: gxhy\in V\}$
is open in
 $V\times V$
, and the map
$V\times V$
, and the map
 $W\to V$
given by
$W\to V$
given by
 $(x,y)\mapsto gxhy$
is strictly differentiable and
$(x,y)\mapsto gxhy$
is strictly differentiable and
 $T_k$
.
$T_k$
.
Indeed, for (a), assume
![]() $x_0\in Z$
. Take
$x_0\in Z$
. Take
![]() $h_1$
generic over h and k generic over
$h_1$
generic over h and k generic over
![]() $g,x,h,h_1$
. Take
$g,x,h,h_1$
. Take
![]() $h_2=h_1^{-1}h$
. Note that
$h_2=h_1^{-1}h$
. Note that
![]() $h_1,h_2\in V$
. Now one writes
$h_1,h_2\in V$
. Now one writes
![]() $f(x)=gxh$
as a composition of strictly differentiable and
$f(x)=gxh$
as a composition of strictly differentiable and
![]() $T_k$
functions defined on an open neighborhood of
$T_k$
functions defined on an open neighborhood of
![]() $x_0$
in the following way. Consider the set
$x_0$
in the following way. Consider the set
![]() $Z_1=\{x\in V:(kg,x)\in Y, (kgx,h_1)\in Y, (kgxh_1,h_2)\in Y, (k^{-1},kgxh)\in Y\}$
. Then by item 2, we have that
$Z_1=\{x\in V:(kg,x)\in Y, (kgx,h_1)\in Y, (kgxh_1,h_2)\in Y, (k^{-1},kgxh)\in Y\}$
. Then by item 2, we have that
![]() $Z_1$
is open, and the map
$Z_1$
is open, and the map
![]() $x\mapsto gxh=k^{-1}(((kgx)h_1)h_2)$
is a composition of strictly differentiable and
$x\mapsto gxh=k^{-1}(((kgx)h_1)h_2)$
is a composition of strictly differentiable and
![]() $T_k$
functions. Also,
$T_k$
functions. Also,
![]() $x_0\in Z_1$
by item 4.
$x_0\in Z_1$
by item 4.
Similarly, for (b), given
![]() $(x_0,y_0)\in W$
, the set
$(x_0,y_0)\in W$
, the set
is open by item (3) and contains
![]() $(x_0,y_0)$
by item (4). And in
$(x_0,y_0)$
by item (4). And in
![]() $W_1$
, the required map is a composition of strictly differentiable and
$W_1$
, the required map is a composition of strictly differentiable and
![]() $T_k$
functions.
$T_k$
functions.
By (1) above and Lemma 6.2, a finite number of translates,
![]() $g_0V,\dots , g_nV$
, cover G. Consider the maps
$g_0V,\dots , g_nV$
, cover G. Consider the maps
![]() $\varphi _i:V\to G$
given by
$\varphi _i:V\to G$
given by
![]() $\varphi _i(x)=g_ix$
. It is straightforward to verify, using (a), (b) and (3) above, that these charts endow G with a (unique) structure of a strictly differentiable or
$\varphi _i(x)=g_ix$
. It is straightforward to verify, using (a), (b) and (3) above, that these charts endow G with a (unique) structure of a strictly differentiable or
![]() $T_k$
manifold, as in Lemma 5.10, and with this structure, G is a Lie group.
$T_k$
manifold, as in Lemma 5.10, and with this structure, G is a Lie group.
For example, to see that the transition maps are strictly differentiable or
![]() $T_k$
, we have to see that the sets
$T_k$
, we have to see that the sets
![]() $V\cap g_i^{-1}g_jV$
are open, and the maps
$V\cap g_i^{-1}g_jV$
are open, and the maps
![]() $\varphi _{i,j}: V\cap g_i^{-1}g_jV\to V\cap g_j^{-1}g_iV$
given by
$\varphi _{i,j}: V\cap g_i^{-1}g_jV\to V\cap g_j^{-1}g_iV$
given by
![]() $x\mapsto g_j^{-1}g_ix$
are strictly differentiable or
$x\mapsto g_j^{-1}g_ix$
are strictly differentiable or
![]() $T_k$
. This is a particular case of (a). Similarly, (b) translates into the multiplication being strictly differentiable or
$T_k$
. This is a particular case of (a). Similarly, (b) translates into the multiplication being strictly differentiable or
![]() $T_k$
and (a) and (3) translate into the inversion being strictly differentiable and
$T_k$
and (a) and (3) translate into the inversion being strictly differentiable and
![]() $T_k$
.
$T_k$
.
When
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, an appropriate version of cell decomposition in Proposition 2.15 gives the result by repeating the above proof. Alternatively, we can see it directly from the result we have just proved and Proposition 5.13 and Lemma 6.2 (and the appropriate version of the Lemma 5.10). Indeed, if G is a definable group in a 1-h-minimal field with
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, an appropriate version of cell decomposition in Proposition 2.15 gives the result by repeating the above proof. Alternatively, we can see it directly from the result we have just proved and Proposition 5.13 and Lemma 6.2 (and the appropriate version of the Lemma 5.10). Indeed, if G is a definable group in a 1-h-minimal field with
![]() $\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, then G has the structure of a weak strictly differentiable or
$\operatorname {\mathrm {acl}}=\operatorname {\mathrm {dcl}}$
, then G has the structure of a weak strictly differentiable or
![]() $T_k$
-Lie group. By Proposition 5.13, there is an open dense
$T_k$
-Lie group. By Proposition 5.13, there is an open dense
![]() $U\subset G$
such that U is a strictly differentiable or
$U\subset G$
such that U is a strictly differentiable or
![]() $T_k$
-manifold. By Proposition 5.11 and Lemma 6.2, a finite number of translates of U cover G,
$T_k$
-manifold. By Proposition 5.11 and Lemma 6.2, a finite number of translates of U cover G,
![]() $g_1U\cup \cdots \cup g_nU=G$
. Then the functions
$g_1U\cup \cdots \cup g_nU=G$
. Then the functions
![]() $\varphi _i:U\to G$
given by
$\varphi _i:U\to G$
given by
![]() $x\mapsto g_ix$
form a gluing data for G which makes it a strictly differentiable or
$x\mapsto g_ix$
form a gluing data for G which makes it a strictly differentiable or
![]() $T_k$
-Lie group.
$T_k$
-Lie group.
As the previous result implies that every definable group G admits a structure of a definable weak Lie group which is unique up to a unique isomorphism, whenever we mention a property of the weak Lie group structure, we understand it with respect to this structure.
Definition 6.5. A definable strictly differentiable local Lie group is given by a definable open set containing a distinguished point
![]() $e\in U\subset K^n$
, a definable open subset
$e\in U\subset K^n$
, a definable open subset
![]() $e\in U_1\subset U$
, and definable strictly differentiable maps
$e\in U_1\subset U$
, and definable strictly differentiable maps
![]() $U_1\times U_1\to U$
denoted as
$U_1\times U_1\to U$
denoted as
![]() $(a,b)\mapsto a\cdot b$
and
$(a,b)\mapsto a\cdot b$
and
![]() $U_1\to U$
denoted as
$U_1\to U$
denoted as
![]() $a\mapsto a^{-1}$
, such that there exists
$a\mapsto a^{-1}$
, such that there exists
![]() $e\in U_2\subset U_1$
definable open such that
$e\in U_2\subset U_1$
definable open such that
-
•
 $a\cdot e=e\cdot a=a$
for
$a\cdot e=e\cdot a=a$
for
 $a\in U_2$
.
$a\in U_2$
. -
• If
 $a,b,c\in U_2$
, then
$a,b,c\in U_2$
, then
 $a\cdot b\in U_1, b\cdot c\in U_1$
and
$a\cdot b\in U_1, b\cdot c\in U_1$
and
 $(a\cdot b)\cdot c=a\cdot (b\cdot c)$
.
$(a\cdot b)\cdot c=a\cdot (b\cdot c)$
. -
• If
 $a\in U_2$
, then
$a\in U_2$
, then
 $a^{-1}\in U_1$
and
$a^{-1}\in U_1$
and
 $a\cdot a^{-1}=a^{-1}\cdot a=e$
.
$a\cdot a^{-1}=a^{-1}\cdot a=e$
.
Given two definable strictly differentiable local Lie groups, U and V, a definable strictly differentiable local Lie group morphism is given by a definable strictly differentiable map
![]() $f:U'\to V_1$
for a
$f:U'\to V_1$
for a
![]() $e\in U'\subset U_1$
open, with
$e\in U'\subset U_1$
open, with
![]() $U_1$
and
$U_1$
and
![]() $V_1$
as in the above definition, and such that
$V_1$
as in the above definition, and such that
![]() $f(e)=e$
,
$f(e)=e$
,
![]() $f(a\cdot b)=f(a)\cdot f(b)$
and
$f(a\cdot b)=f(a)\cdot f(b)$
and
![]() $f(a^{-1})=f(a)^{-1}$
for
$f(a^{-1})=f(a)^{-1}$
for
![]() $a\in U'$
. Also, two such maps
$a\in U'$
. Also, two such maps
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are identified as morphisms if they have the same germ around
$f_2$
are identified as morphisms if they have the same germ around
![]() $0$
– in other words, if there is a definable open neighborhood of the identity
$0$
– in other words, if there is a definable open neighborhood of the identity
![]() $W\subset \operatorname {\mathrm {dom}}(f_1)\cap \operatorname {\mathrm {dom}}(f_2)$
such that
$W\subset \operatorname {\mathrm {dom}}(f_1)\cap \operatorname {\mathrm {dom}}(f_2)$
such that
![]() $f_1|_W=f_2|_W$
.
$f_1|_W=f_2|_W$
.
It is common to only consider local groups where
![]() $e=0$
, and translating, we see that every local group is isomorphic to one with this condition. In this case, we denote the distinguished element by e whenever we emphasise its role as a local group identity.
$e=0$
, and translating, we see that every local group is isomorphic to one with this condition. In this case, we denote the distinguished element by e whenever we emphasise its role as a local group identity.
We will usually identify a local group with its germ at e. In those terms, the prototypical example of a local Lie group is the germ around the identity of a Lie group.
The following fact is a well-known application of the chain rule. We give the short proof for completeness:
Fact 6.6. Suppose U is a local definable strictly differentiable Lie group. Then the multiplication map
![]() $m:U_1 \times U_1\to U$
has derivative
$m:U_1 \times U_1\to U$
has derivative
![]() $m'(0)(u,v)=u+v$
. The inverse
$m'(0)(u,v)=u+v$
. The inverse
![]() $i:U_1\to U$
has derivative
$i:U_1\to U$
has derivative
![]() $i'(0)(x)=-x$
. Raising to power n,
$i'(0)(x)=-x$
. Raising to power n,
![]() $p_n:U_n\to U$
has derivative
$p_n:U_n\to U$
has derivative
![]() $p_n^{\prime }(0)(x)=nx$
.
$p_n^{\prime }(0)(x)=nx$
.
Proof. The formula for
![]() $m'(0)$
follows formally from the equations
$m'(0)$
follows formally from the equations
![]() $m(x,0)=x, m(0,y)=y$
.
$m(x,0)=x, m(0,y)=y$
.
In detail,
![]() $m'(0)(x,y)=ax+by$
for some matrices a and b. If we denote
$m'(0)(x,y)=ax+by$
for some matrices a and b. If we denote
![]() $s(x)=(x,0)$
, we have that
$s(x)=(x,0)$
, we have that
![]() $ms=1$
, so applying the chain rule, we conclude that
$ms=1$
, so applying the chain rule, we conclude that
![]() $m'(0)s'(0)=1$
, and as
$m'(0)s'(0)=1$
, and as
![]() $s'(0)=(1,0)$
, we conclude that
$s'(0)=(1,0)$
, we conclude that
![]() $a=1$
. Similarly, we have
$a=1$
. Similarly, we have
![]() $b=1$
.
$b=1$
.
From this, the formula for
![]() $i'(0)$
follows from
$i'(0)$
follows from
![]() $m(x,i(x))=0$
and the chain rule.
$m(x,i(x))=0$
and the chain rule.
The formula for
![]() $p_n$
follows inductively from the chain rule and
$p_n$
follows inductively from the chain rule and
![]() $p_n(x)= m(p_{n-1}(x),x)$
.
$p_n(x)= m(p_{n-1}(x),x)$
.
We give some results on subgroups and quotient groups. These are not needed for the main applications.
Proposition 6.7. Suppose
![]() $f:G\to H$
is a surjective definable group morphism. Then f is a submersion.
$f:G\to H$
is a surjective definable group morphism. Then f is a submersion.
Proof. This is a consequence of Sard’s Lemma, Proposition 5.21.
Fact 6.8. Suppose X is a topological space and
![]() $Y\subset X$
is a finite union of locally closed subsets of X. Then every open nonempty subset of X contains an open nonempty subset which is either disjoint from Y or contained in Y.
$Y\subset X$
is a finite union of locally closed subsets of X. Then every open nonempty subset of X contains an open nonempty subset which is either disjoint from Y or contained in Y.
Proof. If
![]() $Y_1,Y_2$
are sets satisfying the claim, then so do
$Y_1,Y_2$
are sets satisfying the claim, then so do
![]() $Y_1\cup Y_2$
,
$Y_1\cup Y_2$
,
![]() $Y_1\cap Y_2$
and
$Y_1\cap Y_2$
and
![]() $Y_1\setminus Y_2$
. Since the claim is trivially true if Y is open, the conclusion follows.
$Y_1\setminus Y_2$
. Since the claim is trivially true if Y is open, the conclusion follows.
Proposition 6.9. Suppose G is a definable group and
![]() $H\subset G$
is a definable subgroup. Then H is closed in G.
$H\subset G$
is a definable subgroup. Then H is closed in G.
Proof. Recall that H is a finite union of locally closed subsets of G; see, for instance, Proposition 5.12. So by applying Fact 6.8 to
![]() $H\subset \bar {H}$
, we conclude that H has nonempty relative interior in
$H\subset \bar {H}$
, we conclude that H has nonempty relative interior in
![]() $\bar {H}$
. As H is a subgroup, so is
$\bar {H}$
. As H is a subgroup, so is
![]() $\hat H$
(this is true in any topological group), and we conclude by translation that H is open in
$\hat H$
(this is true in any topological group), and we conclude by translation that H is open in
![]() $\bar {H}$
. An open subgroup is the complement of some of its translates, so it is also closed. We conclude that
$\bar {H}$
. An open subgroup is the complement of some of its translates, so it is also closed. We conclude that
![]() $H=\bar {H}$
is closed.
$H=\bar {H}$
is closed.
Proposition 6.10. Suppose
![]() $H\subset G$
is a subgroup of G. Then with the structure of weak definable strictly differentiable manifolds on G and H, the inclusion
$H\subset G$
is a subgroup of G. Then with the structure of weak definable strictly differentiable manifolds on G and H, the inclusion
![]() $i:H\to G$
is a closed embedding.
$i:H\to G$
is a closed embedding.
Proof. By Proposition 5.20, there is an open dense set
![]() $U\subset H$
such that
$U\subset H$
such that
![]() $i|_{U}$
is an embedding. Replacing U by
$i|_{U}$
is an embedding. Replacing U by
![]() $U'=U\setminus i^{-1}(\operatorname {\mathrm {cl}}(i(H)\setminus i(U)))$
if necessary, and keeping in mind Proposition 2.18 to show
$U'=U\setminus i^{-1}(\operatorname {\mathrm {cl}}(i(H)\setminus i(U)))$
if necessary, and keeping in mind Proposition 2.18 to show
![]() $U'$
is large in H, we may assume
$U'$
is large in H, we may assume
![]() $i(U)$
is open in
$i(U)$
is open in
![]() $i(H)$
. By translation, we conclude that i is an immersion. Also for an open set
$i(H)$
. By translation, we conclude that i is an immersion. Also for an open set
![]() $V\subset H$
, we have that
$V\subset H$
, we have that
![]() $i(V)=i(\bigcup _{h\in H} hU\cap V)=\bigcup _hhi(U\cap h^{-1}V)$
is open in
$i(V)=i(\bigcup _{h\in H} hU\cap V)=\bigcup _hhi(U\cap h^{-1}V)$
is open in
![]() $i(H)$
. Since i is injective, the conclusion follows.
$i(H)$
. Since i is injective, the conclusion follows.
As a consequence of the theorem on constant rank functions, Proposition 4.11, we have the following result:
Corollary 6.11. Suppose U and V are definable strictly differentiable local Lie groups, and let
![]() $g,f:U\to V$
be definable strictly differentiable local Lie group morphisms. If we denote
$g,f:U\to V$
be definable strictly differentiable local Lie group morphisms. If we denote
![]() $Z=\{x\in U: g(x)=f(x)\}$
, then
$Z=\{x\in U: g(x)=f(x)\}$
, then
![]() $\dim _e Z=\dim (\ker (f'(e)-g'(e)))$
.
$\dim _e Z=\dim (\ker (f'(e)-g'(e)))$
.
In particular, if G and H are definable strictly differentiable weak Lie groups and
![]() $g,f$
are definable strictly differentiable Lie group morphisms, then
$g,f$
are definable strictly differentiable Lie group morphisms, then
![]() $\dim \{x: f(x)=g(x)\}=\dim (\ker (f'(e)-g'(e)))$
.
$\dim \{x: f(x)=g(x)\}=\dim (\ker (f'(e)-g'(e)))$
.
Proof. The second result follows from the first because of Lemma 5.8.
To keep the proof readable, we only verify the first statement in the case of weak Lie groups, and in this case, we denote the groups G and H instead of U and V. The proof for local Lie groups is similar. By translating in G, we see that the map
![]() $f\cdot g^{-1}:G\to H$
has, at any point of G, derivatives of constant rank equal to
$f\cdot g^{-1}:G\to H$
has, at any point of G, derivatives of constant rank equal to
![]() $\mathrm {dim}(G)-k$
, for
$\mathrm {dim}(G)-k$
, for
![]() $k=\dim (\text {ker}(f'(e)-g'(e)))$
. Indeed, if
$k=\dim (\text {ker}(f'(e)-g'(e)))$
. Indeed, if
![]() $u\in G$
, then
$u\in G$
, then
![]() $(f\cdot g^{-1})L_u=L_{f(u)}R_{g(u)^{-1}}(f\cdot g^{-1})$
, where
$(f\cdot g^{-1})L_u=L_{f(u)}R_{g(u)^{-1}}(f\cdot g^{-1})$
, where
![]() $L_u$
,
$L_u$
,
![]() $R_u$
denote the left and right translations by u, respectively. By the chain rule, we get
$R_u$
denote the left and right translations by u, respectively. By the chain rule, we get
As
![]() $L_u$
and
$L_u$
and
![]() $L_{f(u)}R_{g(u)}$
are definable strict diffeomorphisms, their derivatives at any point are vector space isomorphisms, so we conclude that the rank of
$L_{f(u)}R_{g(u)}$
are definable strict diffeomorphisms, their derivatives at any point are vector space isomorphisms, so we conclude that the rank of
![]() $(f\cdot g^{-1})'(u)$
equals the rank of
$(f\cdot g^{-1})'(u)$
equals the rank of
![]() $(f\cdot g^{-1})'(e)=f'(e)-g'(e)$
(see Fact 6.6), as desired.
$(f\cdot g^{-1})'(e)=f'(e)-g'(e)$
(see Fact 6.6), as desired.
By the theorem on constant rank functions, Proposition 4.11, we conclude that there are nonempty open sets
![]() $U\subset G$
and
$U\subset G$
and
![]() $V\subset H$
, balls
$V\subset H$
, balls
![]() $B_1, B_2$
and
$B_1, B_2$
and
![]() $B_3$
around the origin and definable strict diffeomorphisms
$B_3$
around the origin and definable strict diffeomorphisms
![]() $\varphi _1:U\to B_1\times B_2$
and
$\varphi _1:U\to B_1\times B_2$
and
![]() $\varphi _2:V\to B_1\times B_3$
, such that
$\varphi _2:V\to B_1\times B_3$
, such that
![]() $f(U)\subset V$
and
$f(U)\subset V$
and
![]() $\varphi _2(f\cdot g^{-1})=\varphi _1\alpha $
for
$\varphi _2(f\cdot g^{-1})=\varphi _1\alpha $
for
![]() $\alpha :B_1\times B_2\to B_1\times B_3$
the function
$\alpha :B_1\times B_2\to B_1\times B_3$
the function
![]() $(x,y)\mapsto (x,0)$
. Note that the dimension of
$(x,y)\mapsto (x,0)$
. Note that the dimension of
![]() $B_2$
is equal to k. Translating in G, we may assume
$B_2$
is equal to k. Translating in G, we may assume
![]() $e\in U$
. More precisely, from the formula
$e\in U$
. More precisely, from the formula
![]() $(f\cdot g^{-1})L_u=(L_{f(u)}R_{g(u)^{-1}})(f\cdot g^{-1})$
discussed before, if
$(f\cdot g^{-1})L_u=(L_{f(u)}R_{g(u)^{-1}})(f\cdot g^{-1})$
discussed before, if
![]() $u\in U$
maps to
$u\in U$
maps to
![]() $(0,0)$
under
$(0,0)$
under
![]() $\varphi _1$
, then
$\varphi _1$
, then
![]() $e\in u^{-1}U$
, so we may replace
$e\in u^{-1}U$
, so we may replace
![]() $(U,V,\varphi _1,\varphi _2)$
by
$(U,V,\varphi _1,\varphi _2)$
by
![]() $(u^{-1}U, f(u)^{-1}Vg(u), \varphi _1L_u, \varphi _2L_{f(u)}R_{g(u)}^{-1})$
. Note also that
$(u^{-1}U, f(u)^{-1}Vg(u), \varphi _1L_u, \varphi _2L_{f(u)}R_{g(u)}^{-1})$
. Note also that
![]() $\varphi _1(e)=(0,0)$
.
$\varphi _1(e)=(0,0)$
.
In this case, we obtain
![]() $\{0\}\times B_2=\varphi _1(Z\cap U)$
, so the local dimension of Z at e is the local dimension of
$\{0\}\times B_2=\varphi _1(Z\cap U)$
, so the local dimension of Z at e is the local dimension of
![]() $\{0\}\times B_2\subset B_1\times B_2$
at
$\{0\}\times B_2\subset B_1\times B_2$
at
![]() $(0,0)$
, which is the dimension of
$(0,0)$
, which is the dimension of
![]() $B_2$
and is as in the statement.
$B_2$
and is as in the statement.
In the particular case where, in the notation of the previous statement,
![]() $\dim (\text {ker}(f'(e)-g'(e)))=\dim (G)$
, we get the following:
$\dim (\text {ker}(f'(e)-g'(e)))=\dim (G)$
, we get the following:
Corollary 6.12. Suppose U and V are definable strictly differentiable local Lie groups, and let
![]() $g,f:U\to V$
be definable strictly differentiable local Lie group morphisms. Then f and g are equal (as local Lie group morphisms) if and only if
$g,f:U\to V$
be definable strictly differentiable local Lie group morphisms. Then f and g are equal (as local Lie group morphisms) if and only if
![]() $f'(0)=g'(0)$
.
$f'(0)=g'(0)$
.
In particular, if G and H are definable strictly differentiable weak Lie groups and
![]() $g,f$
are definable strictly differentiable Lie group morphisms, then f and g coincide in an open neighborhood of the identity e if and only if
$g,f$
are definable strictly differentiable Lie group morphisms, then f and g coincide in an open neighborhood of the identity e if and only if
![]() $f'(e)=g'(e)$
.
$f'(e)=g'(e)$
.
The following two corollaries are not needed for the sequel, but may be interesting on their own right.
Corollary 6.13. Suppose
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are subgroups of the strictly differentiable definable weak Lie group G. Then
$H_2$
are subgroups of the strictly differentiable definable weak Lie group G. Then
![]() $T_e(H_1\cap H_2)=T_e(H_1)\cap T_e(H_2)$
as subspaces of
$T_e(H_1\cap H_2)=T_e(H_1)\cap T_e(H_2)$
as subspaces of
![]() $T_e(G)$
.
$T_e(G)$
.
Proof. This is a consequence of Corollary 6.11. Indeed, we know
![]() $H_1$
,
$H_1$
,
![]() $H_2$
and
$H_2$
and
![]() $H_1\cap H_2$
are strictly differentiable definable weak Lie groups and the inclusion maps
$H_1\cap H_2$
are strictly differentiable definable weak Lie groups and the inclusion maps
![]() $H_1\cap H_2\to H_i$
and
$H_1\cap H_2\to H_i$
and
![]() $H_i\to G$
are strictly differentiable immersions – for example, by Proposition 6.10 – so the statement makes sense. The diagonal map
$H_i\to G$
are strictly differentiable immersions – for example, by Proposition 6.10 – so the statement makes sense. The diagonal map
![]() $\Delta :H_1\cap H_2\to H_1\times H_2$
is the equaliser of the two projections
$\Delta :H_1\cap H_2\to H_1\times H_2$
is the equaliser of the two projections
![]() $p_1:H_1\times H_2\to G$
and
$p_1:H_1\times H_2\to G$
and
![]() $p_2:H_1\times H_2\to G$
. The kernel of
$p_2:H_1\times H_2\to G$
. The kernel of
![]() $p_1^{\prime }(e)-p_2^{\prime }(e)$
is the image under the diagonal map of
$p_1^{\prime }(e)-p_2^{\prime }(e)$
is the image under the diagonal map of
![]() $T_e(H_1)\cap T_e(H_2)$
. So by the equality of the dimensions in Corollary 6.11, we conclude
$T_e(H_1)\cap T_e(H_2)$
. So by the equality of the dimensions in Corollary 6.11, we conclude
![]() $T_e(H_1\cap H_2)=T_e(H_1)\cap T_e(H_2)$
.
$T_e(H_1\cap H_2)=T_e(H_1)\cap T_e(H_2)$
.
Corollary 6.14. If G is a definable strictly differentiable weak Lie group and
![]() $H_1,H_2$
are subgroups, then there is
$H_1,H_2$
are subgroups, then there is
![]() $U\subset G$
an open neighborhood of e such that
$U\subset G$
an open neighborhood of e such that
![]() $U\cap H_1=U\cap H_2$
if and only if
$U\cap H_1=U\cap H_2$
if and only if
![]() $T_e(H_1)=T_e(H_2)$
.
$T_e(H_1)=T_e(H_2)$
.
Proof. By Corollary 6.13, we get
![]() $T_e(H_3)=T_e(H_1)=T_e(H_2)$
for
$T_e(H_3)=T_e(H_1)=T_e(H_2)$
for
![]() $H_3=H_1\cap H_2$
. Then as the inclusion
$H_3=H_1\cap H_2$
. Then as the inclusion
![]() $H_3\to H_1$
produces an isomorphism of tangent spaces at the identity, we conclude by the inverse function Theorem 4.4 that there is
$H_3\to H_1$
produces an isomorphism of tangent spaces at the identity, we conclude by the inverse function Theorem 4.4 that there is
![]() $U\subset G$
an open neighborhood of the identity, such that
$U\subset G$
an open neighborhood of the identity, such that
![]() $U\cap H_1=U\cap H_3$
. Note that this also uses that the topology of
$U\cap H_1=U\cap H_3$
. Note that this also uses that the topology of
![]() $H_1$
and
$H_1$
and
![]() $H_3$
, which makes them strictly differentiable definable Lie groups, coincides with the subgroup topology coming from G; see Proposition 6.10.
$H_3$
, which makes them strictly differentiable definable Lie groups, coincides with the subgroup topology coming from G; see Proposition 6.10.
Symmetrically, we have
![]() $U'\cap H_2=U'\cap H_3$
for some open
$U'\cap H_2=U'\cap H_3$
for some open
![]() $U'$
.
$U'$
.
Next, we give the familiar definition of the Lie bracket in
![]() $T_e(G)$
for the definable Lie group G, and we show it forms a Lie algebra. The exact same definition can also be applied to local Lie groups. For the sake of greater readability, we stick with the former setting.
$T_e(G)$
for the definable Lie group G, and we show it forms a Lie algebra. The exact same definition can also be applied to local Lie groups. For the sake of greater readability, we stick with the former setting.
Definition 6.15. Suppose G is a definable strictly differentiable weak Lie group. For
![]() $g\in G$
, we consider the map
$g\in G$
, we consider the map
![]() $c_g:G\to G$
defined by
$c_g:G\to G$
defined by
![]() $c_g(h)=ghg^{-1}$
. Then
$c_g(h)=ghg^{-1}$
. Then
![]() $c_g$
is a definable group morphism, and so it is strictly differentiable; see Proposition 5.7. So we have a map
$c_g$
is a definable group morphism, and so it is strictly differentiable; see Proposition 5.7. So we have a map
![]() $\mathrm {Ad}:G\to \mathrm {Aut}_K(T_e(G))$
, given by
$\mathrm {Ad}:G\to \mathrm {Aut}_K(T_e(G))$
, given by
![]() $g\mapsto c_g^{\prime }(e)$
. This is a definable map and, by the chain rule, a group morphism (for this recall that
$g\mapsto c_g^{\prime }(e)$
. This is a definable map and, by the chain rule, a group morphism (for this recall that
![]() $c_gc_h=c_{gh}$
). Therefore,
$c_gc_h=c_{gh}$
). Therefore,
![]() $\mathrm {Ad}$
is strictly differentiable, and so its derivative at e gives a linear map
$\mathrm {Ad}$
is strictly differentiable, and so its derivative at e gives a linear map
![]() $\mathrm {ad}:T_e(G)\to \mathrm {End}_K(T_e(G))$
. In other words, this gives a bilinear map
$\mathrm {ad}:T_e(G)\to \mathrm {End}_K(T_e(G))$
. In other words, this gives a bilinear map
![]() $(x,y)\mapsto \mathrm {ad}(x)(y)$
,
$(x,y)\mapsto \mathrm {ad}(x)(y)$
,
![]() $T_e(G)\times T_e(G)\to T_e(G)$
denoted
$T_e(G)\times T_e(G)\to T_e(G)$
denoted
![]() $(x,y)\mapsto [x,y]$
.
$(x,y)\mapsto [x,y]$
.
This map is called the Lie bracket.
Proposition 6.16. Let G be a definable weak
![]() $T_2$
-Lie group. Let
$T_2$
-Lie group. Let
![]() $0\in U\subset K^n$
be an open set and
$0\in U\subset K^n$
be an open set and
![]() $i:U\to G$
a
$i:U\to G$
a
![]() $T_2$
-diffeomorphism of U onto an open subset of G that sends
$T_2$
-diffeomorphism of U onto an open subset of G that sends
![]() $0$
to e. Make U into a local definable group via i. Then under the identification
$0$
to e. Make U into a local definable group via i. Then under the identification
![]() $i'(0):K^n\to T_e(G)$
, the Lie bracket is characterised by the property
$i'(0):K^n\to T_e(G)$
, the Lie bracket is characterised by the property
![]() $x\cdot y\cdot x^{-1}\cdot y^{-1}=[x,y]+O(x,y)^3$
, for
$x\cdot y\cdot x^{-1}\cdot y^{-1}=[x,y]+O(x,y)^3$
, for
![]() $x,y\in U$
.
$x,y\in U$
.
Proof. We use the notation of Definitions 3.7 and 3.8. The function
![]() $f(x,y)=x\cdot y\cdot x^{-1}$
satisfies
$f(x,y)=x\cdot y\cdot x^{-1}$
satisfies
![]() $f(0,y)=y$
and
$f(0,y)=y$
and
![]() $f(x,0)=0$
, so its Taylor approximation of order 2 is of the form
$f(x,0)=0$
, so its Taylor approximation of order 2 is of the form
![]() $f(x,y)=y+axy+O(x,y)^3$
. Indeed, it is of the form
$f(x,y)=y+axy+O(x,y)^3$
. Indeed, it is of the form
![]() $a_0+a_1x+a_2y+a_3x^2+a_4xy+a_5y^2+O(x,y)^3$
, and plugging
$a_0+a_1x+a_2y+a_3x^2+a_4xy+a_5y^2+O(x,y)^3$
, and plugging
![]() $x=0$
and using the uniqueness of the Taylor approximation, we get
$x=0$
and using the uniqueness of the Taylor approximation, we get
![]() $a_0=a_5=0$
and
$a_0=a_5=0$
and
![]() $a_2=1$
, and a similar argument with
$a_2=1$
, and a similar argument with
![]() $y=0$
gives
$y=0$
gives
![]() $a_1=a_3=0$
, so
$a_1=a_3=0$
, so
![]() $f(x,y)=y+axy+O(x,y)^3$
as claimed.
$f(x,y)=y+axy+O(x,y)^3$
as claimed.
From the definition of
![]() $\mathrm {Ad}(x)$
, we get
$\mathrm {Ad}(x)$
, we get
![]() $f(x,y)=\mathrm {Ad}(x)y+O_x(y^2)$
, where
$f(x,y)=\mathrm {Ad}(x)y+O_x(y^2)$
, where
![]() $O_x$
means that the coefficient may depend on x.
$O_x$
means that the coefficient may depend on x.
Note that the definition of
![]() $\mathrm {ad}(x)$
gives
$\mathrm {ad}(x)$
gives
![]() $\mathrm {Ad}(x)(y)=y+[x,y]+O(x^2y)$
. Indeed, we have
$\mathrm {Ad}(x)(y)=y+[x,y]+O(x^2y)$
. Indeed, we have
![]() $\mathrm {Ad}(x)=\mathrm {Ad}(0)+\mathrm {Ad}'(0)(x)+O(x^2)=I+\mathrm {ad}(x)+O(x^2)$
, where I is the identity matrix, and evaluating at y, we conclude
$\mathrm {Ad}(x)=\mathrm {Ad}(0)+\mathrm {Ad}'(0)(x)+O(x^2)=I+\mathrm {ad}(x)+O(x^2)$
, where I is the identity matrix, and evaluating at y, we conclude
![]() $\mathrm {Ad}(x)y=y+[x,y]+O(x^2y)$
.
$\mathrm {Ad}(x)y=y+[x,y]+O(x^2y)$
.
We conclude that
![]() $y+axy+O(x,y)^3=y+[x,y]+O_x(y^2)$
. This implies
$y+axy+O(x,y)^3=y+[x,y]+O_x(y^2)$
. This implies
![]() $[x,y]=axy$
. See Lemma 3.16. Now from
$[x,y]=axy$
. See Lemma 3.16. Now from
![]() $x\cdot y\cdot x^{-1}=y+axy+O(y,x)^3$
, and the formula
$x\cdot y\cdot x^{-1}=y+axy+O(y,x)^3$
, and the formula
![]() $x\cdot y^{-1}=x-y+b_0x^2+b_1xy+b_2y^2+O(x,y)^3$
(see Fact 6.6), we get
$x\cdot y^{-1}=x-y+b_0x^2+b_1xy+b_2y^2+O(x,y)^3$
(see Fact 6.6), we get
![]() $x\cdot y\cdot x^{-1}\cdot y^{-1}=(x\cdot y\cdot x^{-1})\cdot y^{-1}=axy+b_3y^2+O(x,y)^3$
. However, if
$x\cdot y\cdot x^{-1}\cdot y^{-1}=(x\cdot y\cdot x^{-1})\cdot y^{-1}=axy+b_3y^2+O(x,y)^3$
. However, if
![]() $c(x,y)=x\cdot y\cdot x^{-1}\cdot y^{-1}$
, then
$c(x,y)=x\cdot y\cdot x^{-1}\cdot y^{-1}$
, then
![]() $c(0,y)=0$
implies that
$c(0,y)=0$
implies that
![]() $b_3=0$
, as required.
$b_3=0$
, as required.
Lemma 6.17. Let G be a definable weak
![]() $T_3$
-Lie group. Let
$T_3$
-Lie group. Let
![]() $0\in U\subset K^n$
be an open set and
$0\in U\subset K^n$
be an open set and
![]() $i:U\to G$
a
$i:U\to G$
a
![]() $T_3$
-diffeomorphism of U onto an open subset of G that sends
$T_3$
-diffeomorphism of U onto an open subset of G that sends
![]() $0$
to e. Make U into a local definable group via i. Then under the identification
$0$
to e. Make U into a local definable group via i. Then under the identification
![]() $i'(0):K^n\to T_e(G)$
, we have that
$i'(0):K^n\to T_e(G)$
, we have that
![]() $c(x,c(y,z))=[x,[y,z]]+O(x,y,z)^4$
for
$c(x,c(y,z))=[x,[y,z]]+O(x,y,z)^4$
for
![]() $x,y,z\in U$
. Here, we denote
$x,y,z\in U$
. Here, we denote
![]() $c(x,y)=x\cdot y\cdot x^{-1}\cdot y^{-1}$
.
$c(x,y)=x\cdot y\cdot x^{-1}\cdot y^{-1}$
.
Proof. First, we show that
![]() $c(x,y)=[x,y]+a_1xy^2+a_2x^2y+O(x,y)^4$
. Indeed, using Proposition 6.16 and the Taylor expansion of order 3 of c around the origin, we obtain
$c(x,y)=[x,y]+a_1xy^2+a_2x^2y+O(x,y)^4$
. Indeed, using Proposition 6.16 and the Taylor expansion of order 3 of c around the origin, we obtain
![]() $c(x,y)=[x,y]+a_0y^3+a_1xy^2+a_2x^2y+a_3x^3+O(x,y)^4$
. Taking
$c(x,y)=[x,y]+a_0y^3+a_1xy^2+a_2x^2y+a_3x^3+O(x,y)^4$
. Taking
![]() $x=0$
in this formula, we conclude using the uniqueness of Taylor coefficients that
$x=0$
in this formula, we conclude using the uniqueness of Taylor coefficients that
![]() $a_0=0$
. Similarly, taking
$a_0=0$
. Similarly, taking
![]() $y=0$
, we conclude
$y=0$
, we conclude
![]() $a_3=0$
, which finishes the proof of the claim.
$a_3=0$
, which finishes the proof of the claim.
Now we conclude that
![]() $c(x,c(y,z))=[x,c(y,z)]+a_1xc(y,z)^2+a_2x^2c(y,z)+O(x,c(y,z))^4$
. Proposition 6.16 implies that
$c(x,c(y,z))=[x,c(y,z)]+a_1xc(y,z)^2+a_2x^2c(y,z)+O(x,c(y,z))^4$
. Proposition 6.16 implies that
![]() $c(y,z)=O(y,z)^2$
, so
$c(y,z)=O(y,z)^2$
, so
![]() $a_1xc(y,z)^2=O(x,y,z)^5$
and
$a_1xc(y,z)^2=O(x,y,z)^5$
and
![]() $a_2x^2c(y,z)=O(x,y,z)^4$
. Note also that
$a_2x^2c(y,z)=O(x,y,z)^4$
. Note also that
![]() $c(y,z)=[y,z]+O(y,z)^3$
implies
$c(y,z)=[y,z]+O(y,z)^3$
implies
![]() $[x,c(y,z)]=[x,[y,z]]+O(x,y,z)^4$
. Putting all this together, we conclude
$[x,c(y,z)]=[x,[y,z]]+O(x,y,z)^4$
. Putting all this together, we conclude
![]() $c(x,c(y,z))=[x,[y,z]]+O(x,y,z)^4$
, as required.
$c(x,c(y,z))=[x,[y,z]]+O(x,y,z)^4$
, as required.
Remark 6.18. Note that in a definable local strictly differentiable and
![]() $P_1$
-Lie group, we have
$P_1$
-Lie group, we have
![]() $x\cdot y=x+y+O(x,y)^2$
. From this, it follows inductively that
$x\cdot y=x+y+O(x,y)^2$
. From this, it follows inductively that
![]() $x_1\cdot \cdots \cdot x_n=x_1+\cdots +x_n+O(x_1,\cdots ,x_n)^2$
.
$x_1\cdot \cdots \cdot x_n=x_1+\cdots +x_n+O(x_1,\cdots ,x_n)^2$
.
Proposition 6.19. Let G be a definable strictly differentiable weak Lie group. Then
![]() $(T_e(G),[,])$
is a Lie algebra.
$(T_e(G),[,])$
is a Lie algebra.
Proof. We have to prove
![]() $[x,x]=0$
and the Jacobi identity. We will use the characterisation of Proposition 6.16 (we may assume G is
$[x,x]=0$
and the Jacobi identity. We will use the characterisation of Proposition 6.16 (we may assume G is
![]() $T_3$
by Proposition 6.4).
$T_3$
by Proposition 6.4).
![]() $[x,x]=0$
now follows immediately.
$[x,x]=0$
now follows immediately.
The idea of proof of the Jacobi identity is to express
![]() $xyz$
as
$xyz$
as
![]() $f(x,y,z)zyx$
in two different ways using associativity: the first one permutes from left to right, and the second permutes
$f(x,y,z)zyx$
in two different ways using associativity: the first one permutes from left to right, and the second permutes
![]() $yz$
and then permutes from left to right. The details follow.
$yz$
and then permutes from left to right. The details follow.
Writing
![]() $c(x,y)=xyx^{-1}y^{-1}$
, one has
$c(x,y)=xyx^{-1}y^{-1}$
, one has
 $$ \begin{align*} &xyz=c(x,y)yxz=c(x,y)yc(x,z)zx=c(x,y)c(y,c(x,z))c(x,z)yzx= c(x,y)([y,[x,z]]\\&\quad+O(x,y,z)^4)c(x,z)c(y,z)zyx= (c(x,y)+[y,[x,z]]+c(x,z)+c(y,z)+O(x,y,z)^4)zyx. \end{align*} $$
$$ \begin{align*} &xyz=c(x,y)yxz=c(x,y)yc(x,z)zx=c(x,y)c(y,c(x,z))c(x,z)yzx= c(x,y)([y,[x,z]]\\&\quad+O(x,y,z)^4)c(x,z)c(y,z)zyx= (c(x,y)+[y,[x,z]]+c(x,z)+c(y,z)+O(x,y,z)^4)zyx. \end{align*} $$
At the fourth equality, we use Lemma 6.17. At the last step, we use Remark 6.18 together with the estimate
![]() $c(x,y)=O(x,y)^2$
implied by Proposition 6.16 for the error.
$c(x,y)=O(x,y)^2$
implied by Proposition 6.16 for the error.
However,
 $$ \begin{align*}& xyz=xc(y,z)zy=([x,[y,z]]+O(x,y,z)^4)c(y,z)xzy= ([x,[y,z]]\\&\quad +O(x,y,z)^4)c(y,z)c(x,z)zxy= ([x,[y,z]]+ O(x,y,z)^4)c(y,z)c(x,z)zc(x,y)yx= ([x,[y,z]]\\&\quad +O(x,y,z)^4)c(y,z)c(x,z)([z,[x,y]]+O(x,y,z)^4)c(x,y)zyx= ([x,[y,z]]+c(y,z)\\&\quad +c(x,z)+c(x,y)+[z,[x,y]]+O(x,y,z)^4)zyx. \end{align*} $$
$$ \begin{align*}& xyz=xc(y,z)zy=([x,[y,z]]+O(x,y,z)^4)c(y,z)xzy= ([x,[y,z]]\\&\quad +O(x,y,z)^4)c(y,z)c(x,z)zxy= ([x,[y,z]]+ O(x,y,z)^4)c(y,z)c(x,z)zc(x,y)yx= ([x,[y,z]]\\&\quad +O(x,y,z)^4)c(y,z)c(x,z)([z,[x,y]]+O(x,y,z)^4)c(x,y)zyx= ([x,[y,z]]+c(y,z)\\&\quad +c(x,z)+c(x,y)+[z,[x,y]]+O(x,y,z)^4)zyx. \end{align*} $$
From this, we get
![]() $[y,[x,z]]=[x,[y,z]]+[z,[x,y]]+O(x,y,z)^4$
, and from the uniqueness of Taylor expansions, we obtain
$[y,[x,z]]=[x,[y,z]]+[z,[x,y]]+O(x,y,z)^4$
, and from the uniqueness of Taylor expansions, we obtain
![]() $[y,[x,z]]=[x,[y,z]]+[z,[x,y]]$
, which is the Jacobi identity.
$[y,[x,z]]=[x,[y,z]]+[z,[x,y]]$
, which is the Jacobi identity.
Given a strictly differentiable definable weak Lie group G, we denote
![]() $Lie(G)$
the tangent space
$Lie(G)$
the tangent space
![]() $T_e(G)$
considered as a Lie algebra with the Lie bracket
$T_e(G)$
considered as a Lie algebra with the Lie bracket
![]() $[x,y]$
.
$[x,y]$
.
7. Definable fields
In this section, we prove that if L is a definable field in a 1-h-minimal valued field, then, as a definable field, L is isomorphic to a finite field extension of K. This result generalises [Reference Bays and Peterzil2, Theorem 4.2], where this is proved for real closed valued fields, and [Reference Pillay12, Theorem 4.1] where this is proved for p-adically closed fields.
With the terminology and results we have developed in the previous section, the main ingredients of the proof are similar to those appearing in the classification of infinite fields definable in o-minimal fields, [Reference Otero, Peterzil and Pillay10, Theorem 1.1].
Lemma 7.1. Suppose K is a pregeometric field of characteristic
![]() $0$
,
$0$
,
![]() $L\subseteq K$
a definable subfield. Then
$L\subseteq K$
a definable subfield. Then
![]() $L=K$
.
$L=K$
.
Proof.
L is a definable set which is infinite because the characteristic of K is
![]() $0$
. If
$0$
. If
![]() $L\neq K$
, we have a definable injection of L-vector spaces
$L\neq K$
, we have a definable injection of L-vector spaces
![]() $L^2\to K$
, but
$L^2\to K$
, but
![]() $L^2$
has dimension
$L^2$
has dimension
![]() $2$
and K has dimension
$2$
and K has dimension
![]() $1$
, so this is a contradiction.
$1$
, so this is a contradiction.
Lemma 7.2. Suppose K is a pregeometric field of characteristic
![]() $0$
. Let
$0$
. Let
![]() $F_1$
and
$F_1$
and
![]() $F_2$
be finite extensions of K, and consider them as definable fields in K. If
$F_2$
be finite extensions of K, and consider them as definable fields in K. If
![]() $\varphi :F_1\to F_2$
is a definable field morphism, then
$\varphi :F_1\to F_2$
is a definable field morphism, then
![]() $\varphi $
is a morphism of K extensions. In other words, it is the identity when restricted to K.
$\varphi $
is a morphism of K extensions. In other words, it is the identity when restricted to K.
Proof. The set
![]() $\{x\in K: \varphi (x)=x\}$
is a definable subfield of K, so Lemma 7.1 gives the desired conclusion.
$\{x\in K: \varphi (x)=x\}$
is a definable subfield of K, so Lemma 7.1 gives the desired conclusion.
Proposition 7.3. Suppose K is 1-h-minimal and F is a definable field. Then F is isomorphic as a definable field to a finite extension of K. The forgetful functor from finite K-extensions to definable fields is an equivalence of categories.
Proof. That the functor is full is Lemma 7.2.
Let F be a definable field. By Proposition 6.4, we have that
![]() $(F,+)$
is a definable strictly differentiable weak Lie group. If
$(F,+)$
is a definable strictly differentiable weak Lie group. If
![]() $a\in F$
, the map
$a\in F$
, the map
![]() $L_a:x\mapsto ax$
is a definable group morphism and so it is strictly differentiable, by the fullness in Proposition 6.4. We get a definable map
$L_a:x\mapsto ax$
is a definable group morphism and so it is strictly differentiable, by the fullness in Proposition 6.4. We get a definable map
![]() $f:F\to M_n(K)$
defined as
$f:F\to M_n(K)$
defined as
![]() $a\mapsto L_a^{\prime }(0)$
. Here we are identifying the tangent space of F at
$a\mapsto L_a^{\prime }(0)$
. Here we are identifying the tangent space of F at
![]() $0$
with
$0$
with
![]() $K^n$
via taking a fixed chart around
$K^n$
via taking a fixed chart around
![]() $0$
. By the chain rule we have
$0$
. By the chain rule we have
![]() $f(ab)=f(a)f(b)$
for all
$f(ab)=f(a)f(b)$
for all
![]() $a,b\in F$
. Clearly
$a,b\in F$
. Clearly
![]() $f(1)=1$
. Finally one has
$f(1)=1$
. Finally one has
![]() $f(a+b)=f(a)+f(b)$
(the derivative of multiplication
$f(a+b)=f(a)+f(b)$
(the derivative of multiplication
![]() $G\times G\to G$
in a Lie group is the sum map, see for instance Fact 6.6). We conclude that f is a ring map, and because F is a field it is injective. If we set
$G\times G\to G$
in a Lie group is the sum map, see for instance Fact 6.6). We conclude that f is a ring map, and because F is a field it is injective. If we set
![]() $i:K\to M_n(K)$
given by
$i:K\to M_n(K)$
given by
![]() $i(k)=kI$
where I is the identity matrix, then
$i(k)=kI$
where I is the identity matrix, then
![]() $i^{-1}f(F)\subset K$
is a definable subfield of K, and so by Lemma 7.1 one has
$i^{-1}f(F)\subset K$
is a definable subfield of K, and so by Lemma 7.1 one has
![]() $i(K)\subset f(F)$
. So
$i(K)\subset f(F)$
. So
![]() $F/K$
is a finite field extension as required.
$F/K$
is a finite field extension as required.
8. One-dimensional groups are finite by abelian by finite
In this section, we prove that if K is a 1-h-minimal valued field and G is a one-dimensional group definable in K, then G is finite-by-abelian-by-finite. This generalises [Reference Pillay and Yao13, Theorem 2.5], where it is proved that one-dimensional groups definable in p-adically closed fields are abelian-by-finite. This result is analogous to [Reference Pillay11, Corollary 2.16], where it is shown that a one-dimensional group definable in an o-minimal structure is abelian-by-finite.
The proof here is not a straightforward adaptation of either since we do not assume NIP, making the argument more involved.
Definition 8.1. Let G be a group. We let
![]() $C^w$
denote the set of elements
$C^w$
denote the set of elements
![]() $x\in G$
whose centraliser
$x\in G$
whose centraliser
![]() $c_G(x)$
has finite index in G.
$c_G(x)$
has finite index in G.
Note that
![]() $C^w$
is a characteristic subgroup of G.
$C^w$
is a characteristic subgroup of G.
Lemma 8.2. Suppose G is an (abstract) group. Take
![]() $C^w$
as in Definition 8.1, Z its center. Then
$C^w$
as in Definition 8.1, Z its center. Then
![]() $C^w$
and Z are characteristic groups of G, and Z is commutative. Moreover, Z has finite index in G if and only if G is abelian-by-finite.
$C^w$
and Z are characteristic groups of G, and Z is commutative. Moreover, Z has finite index in G if and only if G is abelian-by-finite.
When G is definable in a geometric theory,
![]() $C^w$
and Z are definable. Also,
$C^w$
and Z are definable. Also,
![]() $x\in C^w$
if and only if
$x\in C^w$
if and only if
![]() $\dim (c_G(x))=\dim (G)$
.
$\dim (c_G(x))=\dim (G)$
.
Proof. It is clear that
![]() $C^w$
and Z are characteristic and that Z is abelian. So, in particular, if
$C^w$
and Z are characteristic and that Z is abelian. So, in particular, if
![]() $[G:Z]<\infty $
, then G is abelian-by-finite. However, if A is an abelian subgroup of G of finite index, then
$[G:Z]<\infty $
, then G is abelian-by-finite. However, if A is an abelian subgroup of G of finite index, then
![]() $A\subset C^w$
, as
$A\subset C^w$
, as
![]() $A\subset c_G(a)$
for every
$A\subset c_G(a)$
for every
![]() $a\in A$
. If
$a\in A$
. If
![]() $a_1,\dots , a_n$
are a set of representatives for left cosets of A in
$a_1,\dots , a_n$
are a set of representatives for left cosets of A in
![]() $C^w$
, then
$C^w$
, then
![]() $\bigcap _{k=1}^n c_G(a_k)\cap A\subset Z$
, and as
$\bigcap _{k=1}^n c_G(a_k)\cap A\subset Z$
, and as
![]() $a_k\in C^w$
, the
$a_k\in C^w$
, the
![]() $c_G(a_k)$
have finite index in G, and so Z has finite index in G.
$c_G(a_k)$
have finite index in G, and so Z has finite index in G.
If G is definable in a geometric theory, note that
![]() $x\in C^w$
if and only if
$x\in C^w$
if and only if
![]() $x^G$
, the orbit of G under conjugation, is finite. This is because the fibers of the map
$x^G$
, the orbit of G under conjugation, is finite. This is because the fibers of the map
![]() $x\mapsto x^g$
are cosets of
$x\mapsto x^g$
are cosets of
![]() $c_G(x)$
. So
$c_G(x)$
. So
![]() $C^w$
is definable because a geometric theory eliminates the exist infinity quantifier. We also get that if
$C^w$
is definable because a geometric theory eliminates the exist infinity quantifier. We also get that if
![]() $\dim (c_G(x))=\dim (G)$
, then
$\dim (c_G(x))=\dim (G)$
, then
![]() $c_G(x)$
is of finite index.
$c_G(x)$
is of finite index.
We need the following standard observation:
Lemma 8.3. Suppose
![]() $f:X\times Y\to Z$
is a function definable in a pregeometric theory. Denote
$f:X\times Y\to Z$
is a function definable in a pregeometric theory. Denote
![]() $n=\dim (X)$
and
$n=\dim (X)$
and
![]() $m=\dim (Y)$
. Suppose for all
$m=\dim (Y)$
. Suppose for all
![]() $x\in X$
, the nonempty fibers of the function
$x\in X$
, the nonempty fibers of the function
![]() $f_x(y)=f(x,y)$
have dimension m. Suppose that for all
$f_x(y)=f(x,y)$
have dimension m. Suppose that for all
![]() $y\in Y$
, the nonempty fibers of the function
$y\in Y$
, the nonempty fibers of the function
![]() $f_y(x)=f(x,y)$
have dimension n. Then f has finite image.
$f_y(x)=f(x,y)$
have dimension n. Then f has finite image.
Proof. We claim that the nonempty fibers of f have dimension
![]() $n+m$
. Indeed, if
$n+m$
. Indeed, if
![]() $(x_0,y_0)\in X\times Y$
, then
$(x_0,y_0)\in X\times Y$
, then
![]() $f^{-1}f(x_0,y_0)$
contains
$f^{-1}f(x_0,y_0)$
contains
![]() $\bigcup _{x\in f_{y_0}^{-1}f_{y_0}(x_0)}\{x\}\times f_x^{-1}f_x(y_0)$
, so we conclude by the additivity of dimension.
$\bigcup _{x\in f_{y_0}^{-1}f_{y_0}(x_0)}\{x\}\times f_x^{-1}f_x(y_0)$
, so we conclude by the additivity of dimension.
Lemma 8.4. Suppose G is definable in a pregeometric theory and
![]() $G=C^w$
. Then the image of the commutator map
$G=C^w$
. Then the image of the commutator map
![]() $c:G\times G\to G$
is finite.
$c:G\times G\to G$
is finite.
Proof. The commutator map
![]() $c(x,y)$
is constant when x is fixed and y varies over a right coset of
$c(x,y)$
is constant when x is fixed and y varies over a right coset of
![]() $c_G(x)$
, and it is constant when y is fixed and x varies over a right coset of
$c_G(x)$
, and it is constant when y is fixed and x varies over a right coset of
![]() $c_G(y)$
. This implies that the image of c is finite; see Lemma 8.3.
$c_G(y)$
. This implies that the image of c is finite; see Lemma 8.3.
Lemma 8.5. Suppose G is an n-dimensional group definable in a pregeometric theory such that
![]() $G=C^w$
. Then there is a definable characteristic subgroup,
$G=C^w$
. Then there is a definable characteristic subgroup,
![]() $G_1$
, of finite index with a characteristic finite subgroup L, central in
$G_1$
, of finite index with a characteristic finite subgroup L, central in
![]() $G_1$
, such that
$G_1$
, such that
![]() $G_1/L$
is abelian. If Z is the center of
$G_1/L$
is abelian. If Z is the center of
![]() $G_1$
, then
$G_1$
, then
![]() $Z/L$
contains
$Z/L$
contains
![]() $(G_1/L)^m$
, the m-th powers of
$(G_1/L)^m$
, the m-th powers of
![]() $G_1/L$
, for some m.
$G_1/L$
, for some m.
If the theory is NIP, then the center of G has finite index.
Proof. If the theory has NIP, then the center has finite index in G by Baldwin-Saxl (e.g., [Reference Poizat14, Lemma 1.3]). Indeed,
![]() $Z=\bigcap _{g\in G}c_G(g)$
is an intersection of a definable family subgroups, each of which has finite index by the assumption
$Z=\bigcap _{g\in G}c_G(g)$
is an intersection of a definable family subgroups, each of which has finite index by the assumption
![]() $G=C^w$
. So, as G is NIP, one gets that Z is the intersection of finitely many of the centralisers and
$G=C^w$
. So, as G is NIP, one gets that Z is the intersection of finitely many of the centralisers and
![]() $[G:Z]<\omega $
.
$[G:Z]<\omega $
.
In general, by Lemma 8.4, we know that
![]() $c(G,G)$
is finite. The centraliser of
$c(G,G)$
is finite. The centraliser of
![]() $c(G,G)$
is
$c(G,G)$
is
![]() $G_1$
and has finite index in G by the hypothesis that
$G_1$
and has finite index in G by the hypothesis that
![]() $G=C^w$
. Clearly,
$G=C^w$
. Clearly,
![]() $G_1$
is characteristic in G, so we may replace G by
$G_1$
is characteristic in G, so we may replace G by
![]() $G_1$
and assume that
$G_1$
and assume that
![]() $c(G,G)$
is contained in the center of G.
$c(G,G)$
is contained in the center of G.
In this case, we prove that
![]() $c(G,G)$
generates a finite central characteristic group
$c(G,G)$
generates a finite central characteristic group
![]() ${L=D(G)}$
. Indeed, since
${L=D(G)}$
. Indeed, since
![]() $c(G,G)$
is central, simple computation shows
$c(G,G)$
is central, simple computation shows
![]() $c(gh,x)=c(g,x)c(h,x)$
for all
$c(gh,x)=c(g,x)c(h,x)$
for all
![]() $g,h,x\in G$
. It follows that
$g,h,x\in G$
. It follows that
![]() $c(g,h)^m=c(g^m,h)$
is in
$c(g,h)^m=c(g^m,h)$
is in
![]() $c(G,G)$
. Thus,
$c(G,G)$
. Thus,
![]() $c(g,h)$
has finite order. As
$c(g,h)$
has finite order. As
![]() $c(G,G)$
is central with elements of finite order, the group it generates is central and finite. It is obviously characteristic.
$c(G,G)$
is central with elements of finite order, the group it generates is central and finite. It is obviously characteristic.
We also see that if m is the order of
![]() $D(G)$
, then
$D(G)$
, then
![]() $g^m\in Z$
for all
$g^m\in Z$
for all
![]() $g\in G$
. This is because
$g\in G$
. This is because
![]() $c(g^m,h)=c(g,h)^m=1$
, so
$c(g^m,h)=c(g,h)^m=1$
, so
![]() $(G/D(G))^m$
is contained in
$(G/D(G))^m$
is contained in
![]() $Z/D(G)$
as required.
$Z/D(G)$
as required.
Lemma 8.6. Suppose G is an n-dimensional abelian group definable in a 1-h-minimal theory. Then the m-torsion of G is finite and
![]() $G^m\subset G$
is a subgroup of dimension n.
$G^m\subset G$
is a subgroup of dimension n.
Proof. The map
![]() $x\mapsto x^m$
is a definable group morphism with invertible derivative at the identity – see, for instance, Fact 6.6 – so by Corollary 6.11, we get that the m-torsion of G is finite, and so by additivity of dimension,
$x\mapsto x^m$
is a definable group morphism with invertible derivative at the identity – see, for instance, Fact 6.6 – so by Corollary 6.11, we get that the m-torsion of G is finite, and so by additivity of dimension,
![]() $\dim (G^m)=\dim (G)=n$
.
$\dim (G^m)=\dim (G)=n$
.
Lemma 8.7. Suppose G is an n-dimensional group definable in a 1-h-minimal field. Then
![]() $C^w$
is the kernel of the map
$C^w$
is the kernel of the map
![]() $\mathrm {Ad}:G\to GL_n(K)$
.
$\mathrm {Ad}:G\to GL_n(K)$
.
If the Lie algebra
![]() $\mathrm {Lie}(G)$
is abelian, then
$\mathrm {Lie}(G)$
is abelian, then
![]() $C^w$
has finite index.
$C^w$
has finite index.
Proof. The first statement follows from Corollary 6.12 and Lemma 8.2.
If the Lie bracket is abelian, then, by the definition of the Lie bracket, the derivative of
![]() $\mathrm {Ad}$
at e is
$\mathrm {Ad}$
at e is
![]() $0$
. This means that
$0$
. This means that
![]() $C^w=\ker (\mathrm {Ad})$
contains an open neighborhood of e by Corollary 6.12, so
$C^w=\ker (\mathrm {Ad})$
contains an open neighborhood of e by Corollary 6.12, so
![]() $C^w$
is n-dimensional. By additivity of dimension, we conclude that
$C^w$
is n-dimensional. By additivity of dimension, we conclude that
![]() $C^w$
has finite index in G.
$C^w$
has finite index in G.
Lemma 8.8. Suppose G is an n-dimensional finite-by-abelian group definable in a 1-h-minimal theory. Then
![]() $G=C^w$
, and the center of G has dimension n.
$G=C^w$
, and the center of G has dimension n.
Proof. Let H be a finite normal subgroup such that
![]() $G/H$
is abelian. By elimination of finite imaginaries in fields, we have that
$G/H$
is abelian. By elimination of finite imaginaries in fields, we have that
![]() $G/H$
is definable. Also by Corollary 6.11, we see that the quotient map
$G/H$
is definable. Also by Corollary 6.11, we see that the quotient map
![]() $p:G\to G/H$
induces an isomorphism of tangent spaces at the identity, and under this isomorphism
$p:G\to G/H$
induces an isomorphism of tangent spaces at the identity, and under this isomorphism
![]() $1=\mathrm {Ad}(p(g))=\mathrm {Ad}(g)$
for all
$1=\mathrm {Ad}(p(g))=\mathrm {Ad}(g)$
for all
![]() $g\in G$
. We conclude that
$g\in G$
. We conclude that
![]() $G=C^w$
, by Lemma 8.7. By Lemma 8.5, we get characteristic groups
$G=C^w$
, by Lemma 8.7. By Lemma 8.5, we get characteristic groups
![]() $L\subset G_1\subset G$
such that
$L\subset G_1\subset G$
such that
![]() $G/G_1$
is finite, L is finite,
$G/G_1$
is finite, L is finite,
![]() $G_1/L$
is abelian, and
$G_1/L$
is abelian, and
![]() $Z(G_1)/L\supset (G_1/L)^m$
for some m. Note that as
$Z(G_1)/L\supset (G_1/L)^m$
for some m. Note that as
![]() $G_1$
has finite index in G and
$G_1$
has finite index in G and
![]() $G=C^w$
, we have that
$G=C^w$
, we have that
![]() $Z(G)$
has finite index in
$Z(G)$
has finite index in
![]() $Z(G_1)$
, and so
$Z(G_1)$
, and so
![]() $\dim (Z(G))=\dim (Z(G_1))$
. So we just have to see that
$\dim (Z(G))=\dim (Z(G_1))$
. So we just have to see that
![]() $(G_1/L)^m$
has dimension n. This is, precisely, the conclusion of Lemma 8.6, concluding the proof of the lemma.
$(G_1/L)^m$
has dimension n. This is, precisely, the conclusion of Lemma 8.6, concluding the proof of the lemma.
Proposition 8.9. Suppose K is 1-h-minimal. Suppose G is a strictly differentiable definable weak Lie group. Then
![]() $\mathrm {Lie}(G)$
is abelian if and only if G is finite-by-abelian-by-finite. In this case, G has characteristic definable subgroups
$\mathrm {Lie}(G)$
is abelian if and only if G is finite-by-abelian-by-finite. In this case, G has characteristic definable subgroups
![]() $L\subset G_1\subset G$
such that
$L\subset G_1\subset G$
such that
![]() $G/G_1$
is finite,
$G/G_1$
is finite,
![]() $G_1/L$
is abelian, and L is finite and central in
$G_1/L$
is abelian, and L is finite and central in
![]() $G_1$
. Also, if Z is the center of
$G_1$
. Also, if Z is the center of
![]() $G_1$
, then Z is n-dimensional, and
$G_1$
, then Z is n-dimensional, and
![]() $Z/L$
contains
$Z/L$
contains
![]() $(G_1/L)^m$
for some m.
$(G_1/L)^m$
for some m.
If K is NIP, then we may take
![]() $L=1$
.
$L=1$
.
Proof. First, if
![]() $\mathrm {Lie}(G)$
is abelian, then by Lemma 8.7,
$\mathrm {Lie}(G)$
is abelian, then by Lemma 8.7,
![]() $C^w$
has finite index in G. By Lemma 8.2,
$C^w$
has finite index in G. By Lemma 8.2,
![]() $C^w$
is definable. It is readily checked that
$C^w$
is definable. It is readily checked that
![]() $C^w$
satisfies the assumptions of Lemma 8.5. Putting everything together, we get that G is finite-by-abelian-by-finite. In the other direction, if G is finite-by-abelian-by finite, it has a finite index subgroup whose Lie algebra is commutative, by Lemma 8.8. But then
$C^w$
satisfies the assumptions of Lemma 8.5. Putting everything together, we get that G is finite-by-abelian-by-finite. In the other direction, if G is finite-by-abelian-by finite, it has a finite index subgroup whose Lie algebra is commutative, by Lemma 8.8. But then
![]() $\mathrm {Lie}(G)$
is abelian, too.
$\mathrm {Lie}(G)$
is abelian, too.
So we now proceed under the assumption that
![]() $\mathrm {Lie}(G)$
is abelian. In this case,
$\mathrm {Lie}(G)$
is abelian. In this case,
![]() $C^w$
has finite index in G (by Lemma 8.8), and as
$C^w$
has finite index in G (by Lemma 8.8), and as
![]() $C^w$
is a characteristic subgroup (Lemma 8.2), we may apply lemma 8.5 to
$C^w$
is a characteristic subgroup (Lemma 8.2), we may apply lemma 8.5 to
![]() $C^w$
to get L and
$C^w$
to get L and
![]() $G_1$
, as in the statement. That
$G_1$
, as in the statement. That
![]() $Z(G_1)$
is n-dimensional follows from Lemma 8.8, and so does the fact that
$Z(G_1)$
is n-dimensional follows from Lemma 8.8, and so does the fact that
![]() $(G_1/L)^m\subseteq Z/L$
for some m. In case G is NIP, the application of 8.5 is simpler, as we may take
$(G_1/L)^m\subseteq Z/L$
for some m. In case G is NIP, the application of 8.5 is simpler, as we may take
![]() $G_1$
to be the center of
$G_1$
to be the center of
![]() $C^w$
.
$C^w$
.
Corollary 8.10. Suppose G is a one-dimensional group definable in a 1-h-minimal valued field. Then G is finite-by-abelian-by-finite. If the theory is NIP, then G is abelian-by-finite.
Proof. By Proposition 6.4, we get that G is a strictly differentiable definable weak Lie group. The result now follows from Proposition 8.9 because the only one-dimensional Lie algebra is abelian.
In the NIP case, this corollary follows more directly from the fact that a definable group is definably weakly Lie. Indeed, this implies that there is an element
![]() $x\in G$
with
$x\in G$
with
![]() $x^n\neq e$
(because the derivative of the map
$x^n\neq e$
(because the derivative of the map
![]() $x\mapsto x^n$
at e is
$x\mapsto x^n$
at e is
![]() $v\mapsto nv$
, which is not equal to
$v\mapsto nv$
, which is not equal to
![]() $0$
; see Fact 6.6). By
$0$
; see Fact 6.6). By
![]() $\aleph _0$
-saturation, there is
$\aleph _0$
-saturation, there is
![]() $x\in G$
such that the group generated by x is infinite. Then by [Reference Pillay and Yao13, Remark 2.4], the double centraliser of x has finite index and is abelian. Indeed, note that if
$x\in G$
such that the group generated by x is infinite. Then by [Reference Pillay and Yao13, Remark 2.4], the double centraliser of x has finite index and is abelian. Indeed, note that if
![]() $a\in c_G(x)$
,
$a\in c_G(x)$
,
![]() $c_G(a)$
contains the group generated by x, and so
$c_G(a)$
contains the group generated by x, and so
![]() $\dim (c_G(a))=1$
.
$\dim (c_G(a))=1$
.
The last corollary shows that the classification of one-dimensional abelian groups definable in ACVF carried out in [Reference Acosta1] extends to all definable
![]() $1$
-dimensional groups, for K of characteristic
$1$
-dimensional groups, for K of characteristic
![]() $0$
(see also the main result of [Reference Halevi, Hasson and Peterzil7]). That is, since ACVF
$0$
(see also the main result of [Reference Halevi, Hasson and Peterzil7]). That is, since ACVF
![]() $_0$
is
$_0$
is
![]() $1$
-h-minimal and NIP,
$1$
-h-minimal and NIP,
![]() $1$
-dimensional definable groups are abelian-by-finite, and the classification of definable
$1$
-dimensional definable groups are abelian-by-finite, and the classification of definable
![]() $1$
-dimensional abelian groups of [Reference Acosta1] applies. We do not know if this corollary is true in ACVF
$1$
-dimensional abelian groups of [Reference Acosta1] applies. We do not know if this corollary is true in ACVF
![]() $_{p,p}$
. Similarly, the commutativity assumption is unnecessary in the classification of
$_{p,p}$
. Similarly, the commutativity assumption is unnecessary in the classification of
![]() $1$
-dimensional groups definable in pseudo-local fields of residue characteristic
$1$
-dimensional groups definable in pseudo-local fields of residue characteristic
![]() $0$
. As those are pure henselian, they, too, are
$0$
. As those are pure henselian, they, too, are
![]() $1$
-h-minimal, so we may apply Proposition 8.9. To get the full result, we observe that though pseudo-local fields are not NIP, an inspection of the list of the definable
$1$
-h-minimal, so we may apply Proposition 8.9. To get the full result, we observe that though pseudo-local fields are not NIP, an inspection of the list of the definable
![]() $1$
-dimensional abelian groups obtained in [Reference Acosta1] shows they are almost divisible (i.e., for all n, the map
$1$
-dimensional abelian groups obtained in [Reference Acosta1] shows they are almost divisible (i.e., for all n, the map
![]() $x\mapsto nx$
has finite kernel). Therefore, in the notation of Proposition 8.9, the center of
$x\mapsto nx$
has finite kernel). Therefore, in the notation of Proposition 8.9, the center of
![]() $G_1$
has finite index in
$G_1$
has finite index in
![]() $G_1$
, and so every one-dimensional group is abelian-by-finite.
$G_1$
, and so every one-dimensional group is abelian-by-finite.
Question 8.11. If G is finite-by-abelian, does the center of G have finite index in G? This is true if the theory is NIP or if
![]() $nA$
has finite index in A for every abelian definable group, by Lemmas 8.8 and 8.5.
$nA$
has finite index in A for every abelian definable group, by Lemmas 8.8 and 8.5.
Remark 8.12. ACVF
![]() $_{p,p}$
does not fit into the framework of 1-h-minimality. However, many of the ingredients in previous sections translate to this setting. For example, K is geometric, a subset of
$_{p,p}$
does not fit into the framework of 1-h-minimality. However, many of the ingredients in previous sections translate to this setting. For example, K is geometric, a subset of
![]() $K^n$
has dimension n if and only if it contains a nonempty open set, one-to-finite functions defined in an open set are generically continuous, functions definable in an open set are generically continuous, and K is definably spherically complete.
$K^n$
has dimension n if and only if it contains a nonempty open set, one-to-finite functions defined in an open set are generically continuous, functions definable in an open set are generically continuous, and K is definably spherically complete.
That one-to-finite functions are generically continuous follows from the fact that
![]() $\operatorname {\mathrm {acl}}(a)$
coincides with the field-theoretic algebraic closure of a and by a suitable result about continuity of roots. That functions are generically continuous follows from the fact that
$\operatorname {\mathrm {acl}}(a)$
coincides with the field-theoretic algebraic closure of a and by a suitable result about continuity of roots. That functions are generically continuous follows from the fact that
![]() $\operatorname {\mathrm {dcl}}(a)$
is the Henselization of the perfect closure of a, so a definable function is definably piecewise a composition of rational functions, inverse of the Frobenius automorphism and roots of Hensel polynomials, all of these functions being continuous.
$\operatorname {\mathrm {dcl}}(a)$
is the Henselization of the perfect closure of a, so a definable function is definably piecewise a composition of rational functions, inverse of the Frobenius automorphism and roots of Hensel polynomials, all of these functions being continuous.
However, the inverse of the Frobenius is not differentiable anywhere, so Proposition 3.13 does not hold. Also, the Frobenius is an homeomorphism with
![]() $0$
derivative, so, for example, Proposition 4.6 does not hold.
$0$
derivative, so, for example, Proposition 4.6 does not hold.