No CrossRef data available.
Article contents
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
Published online by Cambridge University Press: 17 April 2024
Abstract
Let 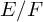 $E/F$ be a quadratic unramified extension of non-archimedean local fields and
$E/F$ be a quadratic unramified extension of non-archimedean local fields and  $\mathbb H$ a simply connected semisimple algebraic group defined and split over F. We establish general results (multiplicities, test vectors) on
$\mathbb H$ a simply connected semisimple algebraic group defined and split over F. We establish general results (multiplicities, test vectors) on 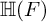 ${\mathbb H} (F)$-distinguished Iwahori-spherical representations of
${\mathbb H} (F)$-distinguished Iwahori-spherical representations of 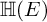 ${\mathbb H} (E)$. For discrete series Iwahori-spherical representations of
${\mathbb H} (E)$. For discrete series Iwahori-spherical representations of 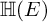 ${\mathbb H} (E)$, we prove a numerical criterion of
${\mathbb H} (E)$, we prove a numerical criterion of 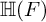 ${\mathbb H} (F)$-distinction. As an application, we classify the
${\mathbb H} (F)$-distinction. As an application, we classify the 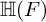 ${\mathbb H} (F)$-distinguished discrete series representations of
${\mathbb H} (F)$-distinguished discrete series representations of 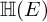 ${\mathbb H} (E)$ corresponding to degree
${\mathbb H} (E)$ corresponding to degree 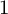 $1$ characters of the Iwahori-Hecke algebra.
$1$ characters of the Iwahori-Hecke algebra.
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 24 , Issue 1 , January 2025 , pp. 1 - 15
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Beuzart-Plessis, R., On distinguished square-integrable representations for Galois pairs and a conjecture of Prasad, Invent. Math. 214(1) (2018), 437–521.CrossRefGoogle Scholar
Borel, A., Admissible representations of a semi-simple group over a local field with vectors fixed under an Iwahori subgroup, Invent. Math. 35 (1976), 233–259.CrossRefGoogle Scholar
Bott, R., An application of the Morse theory to the topology of Lie-groups, Bull. Soc. Math. France 84 (1956), 251–281.CrossRefGoogle Scholar
Broussous, P., Explicit matrix coefficients and test vectors for discrete series representations, arXiv:2005.02904v2.Google Scholar
Broussous, P. and Courtès, F., Distinction of the Steinberg representation, Int. Math. Res. Not. IMRN 2014(11), 3140–3157. With an appendix by François Courtès.CrossRefGoogle Scholar
Bushnell, C. J. and Kutzko, P. C., Smooth representations of reductive
 $p$
-adic groups: structure theory via types, Proc. London Math. Soc. 77(3) (1998), 582–634.CrossRefGoogle Scholar
$p$
-adic groups: structure theory via types, Proc. London Math. Soc. 77(3) (1998), 582–634.CrossRefGoogle Scholar
Casselman, W., The unramified principal series of
 $p$
-adic groups. I. The spherical function, Compos. Math. 40(3) (1980), 387–406.Google Scholar
$p$
-adic groups. I. The spherical function, Compos. Math. 40(3) (1980), 387–406.Google Scholar
Courtès, F., Distinction of the Steinberg representation II: an equality of characters, Forum Math. 27(6) (2015), 346–3475.CrossRefGoogle Scholar
Gurevich, M. and Offen, O., A criterion of integrability of matrix coefficients with respect to a symmetric space, J. Funct. Anal. 270(12) (2016), 4478–4512.CrossRefGoogle Scholar
Gyoja, A., A generalised Poincaré series associated to a Hecke algebra of a finite or
 $p$
-adic Chevalley group, Japan J. Math. 9(1), 1983.CrossRefGoogle Scholar
$p$
-adic Chevalley group, Japan J. Math. 9(1), 1983.CrossRefGoogle Scholar
Iwahori, N., Generalized Tits system (Bruhat decomposition) on
 $p$
-adic semisimple groups, in Algebraic Groups and Discontinuous Subgroups (Proc. Sympos. Pure Math., Boulder, CO, 1965) (Amer. Math. Soc., Providence, RI, 1966), 71–83.CrossRefGoogle Scholar
$p$
-adic semisimple groups, in Algebraic Groups and Discontinuous Subgroups (Proc. Sympos. Pure Math., Boulder, CO, 1965) (Amer. Math. Soc., Providence, RI, 1966), 71–83.CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne Langlands conjecture for Hecke algebras, Invent. Math. 87(1) (1987), 153–215.CrossRefGoogle Scholar
Macdonald, I. G., The Poincaré series of a Coxeter group, Math. Ann. 199 (1972), 161–174.CrossRefGoogle Scholar
Prasad, D., On a conjecture of Jacquet about distinguished representations of GL(n), Duke Math. J. 109(1) (2001), 67–78.CrossRefGoogle Scholar
Reeder, M., On the Iwahori-spherical discrete series for
 $p$
-adic Chevalley groups; formal degrees and
$p$
-adic Chevalley groups; formal degrees and
 $L$
-packets, Ann. Sci. École Norm. Sup. (4) 27(4) (1994), 463–491.CrossRefGoogle Scholar
$L$
-packets, Ann. Sci. École Norm. Sup. (4) 27(4) (1994), 463–491.CrossRefGoogle Scholar
Steinberg, R., Endomorphisms of Linear Algebraic Groups (Memoirs of the American Mathematical Society) no. 80 (American Mathematical Society, Providence, RI, 1968), 108 pp.CrossRefGoogle Scholar
Zhang, C., Local periods for discrete series representations, J. Funct. Anal. 271(6) (2016), 1525–1543.CrossRefGoogle Scholar


