Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T12:20:00.618Z Has data issue: false hasContentIssue false
  • English
  • Français

ONE POSITIVE AND TWO NEGATIVE RESULTS FOR DERIVED CATEGORIES OF ALGEBRAIC STACKS

Part of: Commutative algebra: Homological methods (Co)homology theory Homological algebra Algebraic geometry: Foundations

Published online by Cambridge University Press:  22 January 2018

Jack Hall ,
Amnon Neeman  and
David Rydh
Jack Hall
Affiliation:
Department of Mathematics, University of Arizona, Tucson, AZ 85721-0089, USA (jackhall@math.arizona.edu)
Amnon Neeman
Affiliation:
Mathematical Sciences Institute, The Australian National University, Acton, ACT 2601, Australia (Amnon.Neeman@anu.edu.au)
David Rydh
Affiliation:
KTH Royal Institute of Technology, Department of Mathematics, SE-100 44 Stockholm, Sweden (dary@math.kth.se)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 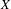$X$ be a quasi-compact and quasi-separated scheme. There are two fundamental and pervasive facts about the unbounded derived category of 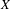$X$: (1) 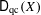$\mathsf{D}_{\text{qc}}(X)$ is compactly generated by perfect complexes and (2) if 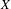$X$ is noetherian or has affine diagonal, then the functor 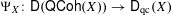$\unicode[STIX]{x1D6F9}_{X}:\mathsf{D}(\mathsf{QCoh}(X))\rightarrow \mathsf{D}_{\text{qc}}(X)$ is an equivalence. Our main results are that for algebraic stacks in positive characteristic, the assertions (1) and (2) are typically false.

Keywords

derived categoriesalgebraic stacks

MSC classification

Primary: 14F05: Sheaves, derived categories of sheaves and related constructions
Secondary: 13D09: Derived categories 14A20: Generalizations (algebraic spaces, stacks) 18G10: Resolutions; derived functors
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 5 , September 2019 , pp. 1087 - 1111
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first and second author are supported by the Australian Research Council (ARC), grant numbers FL100100137, DE150101799, and DP150102313. The third author is supported by the Swedish Research Council (VR), grant numbers 2011-5599 and 2015-05554.

References

Alper, J., Hall, J. and Rydh, D., A Luna étale slice theorem for algebraic stacks, preprint, 2015, arXiv:1504.06467.Google Scholar
Bondal, A. and Van den Bergh, M., Generators and representability of functors in commutative and noncommutative geometry, Mosc. Math. J. 3(1) (2003), 1–36, 258.Google Scholar
Bhatt, B., private communication, Sept–Oct 2012.Google Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., Stratifying modular representations of finite groups, Ann. of Math. (2) 174(3) (2011), 1643–1684.Google Scholar
Bökstedt, M. and Neeman, A., Homotopy limits in triangulated categories, Compos. Math. 86(2) (1993), 209–234.Google Scholar
Borel, A., Linear Algebraic Groups, 2nd edn, Graduate Texts in Mathematics, Volume 126 (Springer, New York, 1991).Google Scholar
Brion, M., On linearization of line bundles, J. Math. Sci. Univ. Tokyo 22(1) (2015), 113–147.Google Scholar
Ben-Zvi, D., Compact generation for modular representations, MathOverflow, Nov 2009, http://mathoverflow.net/q/4965.Google Scholar
Ben-Zvi, D., Francis, J. and Nadler, D., Integral transforms and Drinfeld centers in derived algebraic geometry, J. Amer. Math. Soc. 23(4) (2010), 909–966.Google Scholar
Conrad, B., A modern proof of Chevalley’s theorem on algebraic groups, J. Ramanujan Math. Soc. 17(1) (2002), 1–18.Google Scholar
Demazure, M. and Gabriel, P., Groupes algébriques. Tome I: Géométrie algébrique, généralités, groupes commutatifs, Masson & Cie, Éditeur, Paris, 1970, Avec un appendice Corps de classes local par Michiel Hazewinkel.Google Scholar
Drinfeld, V. and Gaitsgory, D., On some finiteness questions for algebraic stacks, Geom. Funct. Anal. 23(1) (2013), 149–294.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique III. Étude cohomologique des faisceaux cohérents. I, Publ. Math. Inst. Hautes Études Sci. 11 (1961), 167 pp.Google Scholar
Gross, P., Tensor generators on schemes and stacks, Algebr. Geom. 4(4) (2017), 501–522.Google Scholar
Lurie, J., Higher Algebra, available on homepage, May 2016.Google Scholar
Hall, J., Cohomology and base change for algebraic stacks, Math. Z. 278(1–2) (2014), 401–429.Google Scholar
Hartshorne, R., Residues and duality, Lecture Notes of a Seminar on the Work of A. Grothendieck, Given at Harvard 1963/64. With an Appendix by P. Deligne, Lecture Notes in Mathematics, Volume 20 (Springer, Berlin, 1966).Google Scholar
Hall, J. and Rydh, D., Coherent Tannaka duality and algebraicity of Hom-stacks, preprint, 2014, arXiv:1405.7680.Google Scholar
Hall, J. and Rydh, D., Algebraic groups and compact generation of their derived categories of representations, Indiana Univ. Math. J. 64(6) (2015), 1903–1923.Google Scholar
Hall, J. and Rydh, D., Perfect complexes on algebraic stacks, Compos. Math. 153(11) (2017), 2318–2367.Google Scholar
Lurie, J., Higher Topos Theory, Annals of Mathematics Studies, Volume 170 (Princeton University Press, Princeton, NJ, 2009).Google Scholar
Krishna, A., Perfect complexes on Deligne–Mumford stacks and applications, J. K-Theory 4(3) (2009), 559–603.Google Scholar
Kashiwara, M. and Schapira, P., Categories and sheaves, Grundlehren der Mathematischen Wissenschaften, Fundamental Principles of Mathematical Sciences, Volume 332 (Springer, Berlin, 2006).Google Scholar
Lieblich, M., Moduli of twisted sheaves and generalized Azumaya algebras, ProQuest LLC, Ann Arbor, MI, 2004, Thesis (PhD)–Massachusetts Institute of Technology.Google Scholar
Laumon, G. and Moret-Bailly, L., Champs algébriques, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 39 (Springer, Berlin, 2000).Google Scholar
Lurie, J., Tannaka duality for geometric stacks, preprint, 2004, arXiv:0412266, p. 14.Google Scholar
Neeman, A., The Grothendieck duality theorem via Bousfield’s techniques and Brown representability, J. Amer. Math. Soc. 9(1) 205–236.Google Scholar
Neeman, A., On the derived category of sheaves on a manifold, Doc. Math. 6 (2001), 483–488. (electronic).Google Scholar
Neeman, A., Triangulated Categories, Annals of Mathematics Studies, Volume  148 (Princeton University Press, Princeton, NJ, 2001).Google Scholar
Neeman, A., Non-left-complete derived categories, Math. Res. Lett. 18(5) (2011), 827–832.Google Scholar
Neeman, A., The homotopy category of injectives, Algebra Number Theory 8(2) (2014), 429–456.Google Scholar
Olsson, M., Sheaves on Artin stacks, J. Reine Angew. Math. 603 (2007), 55–112.Google Scholar
Rosenlicht, M., On quotient varieties and the affine embedding of certain homogeneous spaces, Trans. Amer. Math. Soc. 101 (1961), 211–223.Google Scholar
Rydh, D., Étale dévissage, descent and pushouts of stacks, J. Algebra 331 (2011), 194–223.Google Scholar
Rydh, D., Noetherian approximation of algebraic spaces and stacks, J. Algebra 422 (2015), 105–147.Google Scholar
Serpé, C., Resolution of unbounded complexes in Grothendieck categories, J. Pure Appl. Algebra 177(1) (2003), 103–112.Google Scholar
Théorie des intersections et théorème de Riemann–Roch, Lecture Notes in Mathematics, Volume 225(Springer, Berlin, 1971). Séminaire de Géométrie Algébrique du Bois-Marie 1966–1967 (SGA 6), Dirigé par P. Berthelot, A. Grothendieck et L. Illusie. Avec la collaboration de D. Ferrand, J. P. Jouanolou, O. Jussila, S. Kleiman, M. Raynaud et J. P. Serre.Google Scholar
Spaltenstein, N., Resolutions of unbounded complexes, Compos. Math. 65(2) (1988), 121–154.Google Scholar
The Stacks Project Authors, Stacks Project, http://stacks.math.columbia.edu.Google Scholar
Sumihiro, H., Equivariant completion, Kyoto J. Math. Univ. 14 (1974), 1–28.Google Scholar
Toën, B., Derived Azumaya algebras and generators for twisted derived categories, Invent. Math. 189(3) (2012), 581–652.Google Scholar
Totaro, B., The resolution property for schemes and stacks, J. Reine Angew. Math. 577 (2004), 1–22.Google Scholar
Thomason, R. W. and Trobaugh, T., Higher algebraic K-theory of schemes and of derived categories, in The Grothendieck Festschrift, Volume III, Progress in Mathematics, Volume 88, pp. 247–435 (Birkhäuser Boston, Boston, MA, 1990).Google Scholar