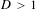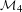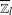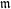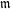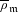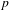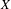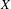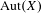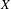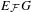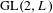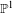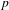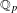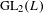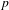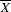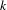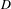Contents
Research Article
A CATEGORIFICATION OF A QUANTUM FROBENIUS MAP
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2017, pp. 899-939
-
- Article
- Export citation
ORBIFOLD POINTS ON PRYM–TEICHMÜLLER CURVES IN GENUS
 $4$
$4$
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2017, pp. 673-706
-
- Article
- Export citation
DUBROVIN’S SUPERPOTENTIAL AS A GLOBAL SPECTRAL CURVE
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2017, pp. 449-497
-
- Article
- Export citation
ON THE COHOMOLOGY OF SOME SIMPLE SHIMURA VARIETIES WITH BAD REDUCTION
- Part of:
-
- Published online by Cambridge University Press:
- 06 December 2016, pp. 1-24
-
- Article
- Export citation
QUANTUM TEICHMÜLLER SPACES AND QUANTUM TRACE MAP
- Part of:
-
- Published online by Cambridge University Press:
- 06 April 2017, pp. 249-291
-
- Article
- Export citation
INVOLUTIVE HEEGAARD FLOER HOMOLOGY AND PLUMBED THREE-MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2017, pp. 1115-1155
-
- Article
- Export citation
HOMOGENEOUS SPACE FIBRATIONS OVER SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2017, pp. 293-327
-
- Article
- Export citation
AX–SCHANUEL CONDITION IN ARBITRARY CHARACTERISTIC
- Part of:
-
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1157-1213
-
- Article
- Export citation
SUR LA TORSION DANS LA COHOMOLOGIE DES VARIÉTÉS DE SHIMURA DE KOTTWITZ-HARRIS-TAYLOR
- Part of:
-
- Published online by Cambridge University Press:
- 30 March 2017, pp. 499-517
-
- Article
- Export citation
SPECTRAL TRANSFER FOR METAPLECTIC GROUPS. I. LOCAL CHARACTER RELATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2016, pp. 25-123
-
- Article
- Export citation
SYMMETRIC OPERADS IN ABSTRACT SYMMETRIC SPECTRA
- Part of:
-
- Published online by Cambridge University Press:
- 25 May 2018, pp. 707-758
-
- Article
- Export citation
CM RELATIONS IN FIBERED POWERS OF ELLIPTIC FAMILIES
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2017, pp. 941-956
-
- Article
- Export citation
WHITTAKER FUNCTIONS AND DEMAZURE CHARACTERS
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2017, pp. 759-781
-
- Article
- Export citation
K-STABILITY OF FANO MANIFOLDS WITH NOT SMALL ALPHA INVARIANTS
- Part of:
-
- Published online by Cambridge University Press:
- 30 March 2017, pp. 519-530
-
- Article
- Export citation
ON THE MILNOR MONODROMY OF THE IRREDUCIBLE COMPLEX REFLECTION ARRANGEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1215-1231
-
- Article
- Export citation
BETTI NUMBER ESTIMATES IN
 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2017, pp. 957-991
-
- Article
- Export citation
DISMANTLABLE CLASSIFYING SPACE FOR THE FAMILY OF PARABOLIC SUBGROUPS OF A RELATIVELY HYPERBOLIC GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2017, pp. 329-345
-
- Article
- Export citation
LOCALLY ANALYTIC REPRESENTATIONS OF
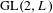 $\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF
$\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF 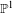 $\mathbb{P}^{1}$
$\mathbb{P}^{1}$
- Part of:
-
- Published online by Cambridge University Press:
- 12 January 2017, pp. 125-187
-
- Article
- Export citation
RELATIVE CYCLES WITH MODULI AND REGULATOR MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 1233-1293
-
- Article
- Export citation
A VARIANT OF HARISH-CHANDRA FUNCTORS
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2017, pp. 993-1049
-
- Article
- Export citation