Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T05:25:47.507Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVE CYCLES WITH MODULI AND REGULATOR MAPS

Part of: Cycles and subschemes (Co)homology theory

Published online by Cambridge University Press:  02 November 2017

Federico Binda Open the ORCID record for Federico Binda [Opens in a new window]  and
Shuji Saito
Federico Binda
Affiliation:
Fakultät für Mathematik, Universität Duisburg-Essen, Thea-Leymann Strasse 9, 45127 Essen, Germany Fakultät für Mathematik, Universität Regensburg, 93040, Regensburg, Germany (federico.binda@ur.de)
Shuji Saito
Affiliation:
Interactive Research Center of Science, Graduate School of Science and Engineering, Tokyo Institute of Technology, Ookayama, Meguro, Tokyo 152-8551, Japan (sshuji@msb.biglobe.ne.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 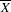$\overline{X}$ be a separated scheme of finite type over a field 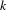$k$ and 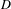$D$ a non-reduced effective Cartier divisor on it. We attach to the pair 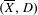$(\overline{X},D)$ a cycle complex with modulus, those homotopy groups – called higher Chow groups with modulus – generalize additive higher Chow groups of Bloch–Esnault, Rülling, Park and Krishna–Levine, and that sheafified on 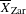$\overline{X}_{\text{Zar}}$ gives a candidate definition for a relative motivic complex of the pair, that we compute in weight $1$. When 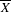$\overline{X}$ is smooth over 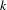$k$ and 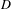$D$ is such that 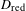$D_{\text{red}}$ is a normal crossing divisor, we construct a fundamental class in the cohomology of relative differentials for a cycle satisfying the modulus condition, refining El Zein’s explicit construction of the fundamental class of a cycle. This is used to define a natural regulator map from the relative motivic complex of $(\overline{X},D)$ to the relative de Rham complex. When 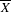$\overline{X}$ is defined over 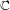$\mathbb{C}$, the same method leads to the construction of a regulator map to a relative version of Deligne cohomology, generalizing Bloch’s regulator from higher Chow groups. Finally, when 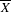$\overline{X}$ is moreover connected and proper over 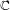$\mathbb{C}$, we use relative Deligne cohomology to define relative intermediate Jacobians with modulus 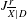$J_{\overline{X}|D}^{r}$ of the pair 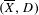$(\overline{X},D)$. For 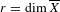$r=\dim \overline{X}$, we show that 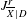$J_{\overline{X}|D}^{r}$ is the universal regular quotient of the Chow group of $0$-cycles with modulus.

Keywords

algebraic geometryK-theory

MSC classification

Primary: 14C25: Algebraic cycles
Secondary: 14C30: Transcendental methods, Hodge theory , Hodge conjecture 14F42: Motivic cohomology; motivic homotopy theory 14F43: Other algebro-geometric (co)homologies (e.g., intersection, equivariant, Lawson, Deligne (co)homologies)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 6 , November 2019 , pp. 1233 - 1293
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barbieri-Viale, L. and Srinivas, V., Albanese and Picard 1-motives, Mém. Soc. Math. Fr. (N.S.) (87) (2001), vi+104 pp.Google Scholar
Beilinson, A., Height pairing between algebraic cycles, in Current Trends in Arithmetical Algebraic Geometry (Arcata, California, 1985), Contemporary Mathematics, Volume 67, pp. 1–24 (American Mathematical Society, Providence, RI, 1987).Google Scholar
Binda, F., Motives and algebraic cycles with moduli conditions, PhD Thesis, University of Duisburg-Essen (2016).Google Scholar
Binda, F., A cycle class map from Chow groups with modulus to relative $K$ -theory, Preprint, 2017, arXiv:1706.07126 [math.AG].Google Scholar
Binda, F. and Krishna, A., Zero cycles with modulus and zero cycles on singular varieties, Compos. Math. 154(1) (2018), 120–187.Google Scholar
Bloch, S., Algebraic cycles and higher K-theory, Adv. Math. 61 (1986), 267–304.Google Scholar
Bloch, S., Algebraic cycles and the Beĭlinson conjectures, in The Lefschetz Centennial Conference, Part I (Mexico City, 1984), Contemporary Mathematics, Volume 58, pp. 65–79 (Amer. Math. Soc., Providence, RI, 1986).Google Scholar
Bloch, S., Algebraic cycles and the Lie algebra of mixed Tate motives, J. Amer. Math. Soc. (JAMS) 4 (1991), 771–791.Google Scholar
Bloch, S., Letter to Bruno Kahn, October 2001.Google Scholar
Bloch, S. and Esnault, H., The additive dilogarithm. Kazuya Kato’s fiftieth birthday, Doc. Math. Extra Vol. (2003), 131–155.Google Scholar
Bloch, S. and Esnault, H., An additive version of higher Chow groups, in Annales Scientifiques de l’École Normale Supérieure, Volume 36, pp. 463–477 (Elsevier, 2003).Google Scholar
Bloch, S. and Srinivas, V., Enriched Hodge structures, in Algebra, Arithmetic and Geometry, Part I, II (Mumbai, 2000), Tata Institute of Fundamental Research Studies in Mathematics, Volume 16, pp. 171–184 (Tata Inst. Fund. Res., Bombay, 2002).Google Scholar
Carlson, J., Extensions of mixed Hodge structures, in Journées de geométrie algébrique d’Angers, Juillet 1979, pp. 107–127 (Sijtho & Noordho, Alphen aan den Rijn—Germantown, MD., 1980).Google Scholar
Conrad, B., Grothendieck Duality and Base Change, Lecture Notes in Mathematics, Volume 1750, vi+296pp (Springer, Berlin, 2000). ISBN: 3-540-41134-8.Google Scholar
Deligne, P., Équations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, Volume 163, iii+133 pp (Springer, Berlin–New York, 1970).Google Scholar
Deligne, P., Théorie de Hodge. II, Publ. Math. Inst. Hautes Études Sci. (40) (1971), 5–57.Google Scholar
El Zein, F., Complexe dualisant et applications à la classe fondamentale d’un cycle, Mém. Soc. Math. Fr. (N.S.) 58 (1978), 1–66.Google Scholar
Esnault, H., Srinivas, V. and Viehweg, E., The universal regular quotient of the chow group of points on projective varieties, Invent. Math. 135 (1999), 595–664.Google Scholar
Esnault, H. and Viehweg, E., Deligne-Beĭlinson cohomology, in Beĭlinson’s conjectures on special values of L-functions, Perspect. Math., Volume 4, pp. 43–91 (Academic Press, Boston, MA, 1988).Google Scholar
Esnault, H. and Wittenberg, O., On the cycle class map for zero-cycles over local fields. (With an appendix by Spencer Bloch.), Ann. Sci. Éc. Norm. Supér. (4) 49(2) (2016), 483–520.Google Scholar
Friedlander, E. M. and Suslin, A., The spectral sequence relating algebraic K-theory to motivic cohomology, Ann. Sc. Éc. Norm. Supér. (4) 35 (2002), 773–875.Google Scholar
Fulton, W., Intersection theory, in Ergebnisse der Mathematik und ihrer Grenzgebiete (3 [Results in Mathematics and Related Areas (3)], Volume 2 (Springer, Berlin, 1984).Google Scholar
Gros, M., Classes de Chern et classes de cycles en cohomologie de Hodge–Witt logarithmique, Mém. Soc. Math. France (N.S.) (21) (1985), 87.Google Scholar
Grothendieck, A., The cohomology theory of abstract algebraic varieties, in Proc. Internat. Congress Math. (Edinburgh, 1958), pp. 103–118 (Cambridge Univ. Press, New York, 1960).Google Scholar
Hartshorne, R., Residues and duality, in Lecture Notes of a Seminar on the Work of A. Grothendieck, Given at Harvard 1963/64. With an appendix by P. Deligne, Lecture Notes in Mathematics, Volume 20, vii+423 pp (Springer, Berlin–New York, 1966).Google Scholar
Hartshorne, R., On the De Rham cohomology of algebraic varieties, Publ. Math. Inst. Hautes Etudes Sci. 45 (1975), 6–99.Google Scholar
Iwasa, R. and Kai, W., Chern classes with modulus, Preprint, 2016, arXiv:1611.07882v2 [math.KT].Google Scholar
Kahn, B., Saito, S. and Yamazaki, T., Reciprocity sheaves. (With two appendices by Kay Rülling.), Compos. Math. 152(9) (2016), 1851–1898.Google Scholar
Kai, W., A moving lemma for algebraic cycles with modulus and contravariance, Preprint, 2016, arXiv:1507.07619v3.Google Scholar
Kato, K. and Russell, H., Albanese varieties with modulus and Hodge theory, Ann. Inst. Fourier (Grenoble) 62 (2012), 783–806.Google Scholar
Kato, K., Saito, S. and Sato, K., $p$ -adic vanishing cycles and $p$ -adic étale tate twists on generalized semistable families, Preprint, 2014.Google Scholar
Kerz, M. and Saito, S., Chow group of 0-cycles with modulus and higher-dimensional class field theory, Duke Math. J. 165 (2016), 2811–2897.Google Scholar
Krishna, A., On 0-cycles with modulus, Algebra Number Theory 9 (2015), 2397–2415.Google Scholar
Krishna, A. and Levine, M., Additive higher Chow groups of schemes, J. Reine Angew. Math. 619 (2008), 75–140.Google Scholar
Krishna, A. and Park, J., Moving lemma for additive higher Chow groups, Algebra Number Theory 6 (2012), 293–326.Google Scholar
Levine, M., Mixed Motives, Mathematical Surveys and Monographs, Volume 57 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Levine, M., Techniques of localization in the theory of algebraic cycles, J. Algebraic Geom. 10 (2001), 299–363.Google Scholar
Levine, M., The homotopy coniveau tower, J. Topol. 1 (2008), 217–267.Google Scholar
Levine, M., Smooth motives, in Motives and Algebraic Cycles, Fields Inst. Commun., Volume 56, pp. 175–231 (American Mathematical Society, Providence, RI, 2009).Google Scholar
Morrow, M., Pro cdh-descent for cyclic homology and K-theory, J. Inst. Math. Jussieu 15 (2016), 539–567.Google Scholar
Park, J., Regulators on additive higher Chow groups, Amer. J. Math. 131 (2009), 257–276.Google Scholar
Rülling, K., The generalized de Rham–Witt complex over a field is a complex of zero-cycles, J. Algebraic Geom. 16 (2007), 109–169.Google Scholar
Rülling, K. and Saito, S., Higher Chow groups with modulus and relative Milnor k-theory, Trans. Amer. Math. Soc. (2016), doi:10.1090/tran/7018, Article electronically published on September 7, 2017.Google Scholar
Russell, H., Albanese varieties with modulus over a perfect field, Algebra Number Theory 7 (2013), 853–892.Google Scholar
Sato, K., Logarithmic Hodge–Witt sheaves on normal crossing varieties, Math. Z. 257 (2007), 707–743.Google Scholar
Sato, K., Cycle classes for p-adic étale Tate twists and the image of p-adic regulators, Doc. Math. 18 (2013), 177–247.Google Scholar
Serre, J.-P., Groupes algébriques et corps de classes, in Publications de l’Institut Mathématique de l’Université de Nancago [Publications of the Mathematical Institute of the University of Nancago], 2nd edn, Actualités Scientifiques et Industrielles [Current Scientific and Industrial Topics], Volume 7, p. 1264 (Hermann, Paris, 1959).Google Scholar
Voevodsky, V., Cohomological theory of presheaves with transfers, in Cycles, Transfers, and Motivic Homology Theories, Ann. of Math. Stud. Volume 143, pp. 87–137 (Princeton University Press, Princeton, NJ, 2000).Google Scholar
Voevodsky, V., Motivic cohomology groups are isomorphic to higher Chow groups in any characteristic, Int. Math. Res. Not. IMRN (7) (2002), 351–355.Google Scholar