Article contents
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS
Published online by Cambridge University Press: 25 November 2024
Abstract
In [CDD22], we investigated the structure of  $\ast $-isomorphisms between von Neumann algebras
$\ast $-isomorphisms between von Neumann algebras 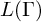 $L(\Gamma )$ associated with graph product groups
$L(\Gamma )$ associated with graph product groups 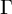 $\Gamma $ of flower-shaped graphs and property (T) wreath-like product vertex groups, as in [CIOS21]. In this follow-up, we continue the structural study of these algebras by establishing that these graph product groups
$\Gamma $ of flower-shaped graphs and property (T) wreath-like product vertex groups, as in [CIOS21]. In this follow-up, we continue the structural study of these algebras by establishing that these graph product groups 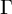 $\Gamma $ are entirely recognizable from the category of all von Neumann algebras arising from an arbitrary nontrivial graph product group with infinite vertex groups. A sharper
$\Gamma $ are entirely recognizable from the category of all von Neumann algebras arising from an arbitrary nontrivial graph product group with infinite vertex groups. A sharper 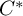 $C^*$-algebraic version of this statement is also obtained. In the process of proving these results, we also extend the main
$C^*$-algebraic version of this statement is also obtained. In the process of proving these results, we also extend the main 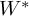 $W^*$-superrigidity result from [CIOS21] to direct products of property (T) wreath-like product groups.
$W^*$-superrigidity result from [CIOS21] to direct products of property (T) wreath-like product groups.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 24 , Issue 1 , January 2025 , pp. 117 - 156
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
This article was originally published without funding information. The error has been corrected and the online HTML and PDF versions updated.
References
A correction has been issued for this article:
- 2
- Cited by
Linked content
Please note a has been issued for this article.


