Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T16:45:00.315Z Has data issue: false hasContentIssue false
  • English
  • Français

SUR LA TORSION DANS LA COHOMOLOGIE DES VARIÉTÉS DE SHIMURA DE KOTTWITZ-HARRIS-TAYLOR

Part of: Representation theory of groups Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  30 March 2017

Pascal Boyer
Pascal Boyer*
Affiliation:
Université Paris 13, Sorbonne Paris Cité, LAGA, CNRS, UMR 7539, 93430, Villetaneuse (France), PerCoLaTor: ANR-14-CE25, France (boyer@math.univ-paris13.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

(Torsion in the cohomology of Kottwitz–Harris–Taylor Shimura varieties) When the level at 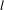$l$ of a Shimura variety of Kottwitz–Harris–Taylor is not maximal, its cohomology with coefficients in a 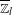$\overline{\mathbb{Z}}_{l}$-local system isn’t in general torsion free. In order to prove torsion freeness results of the cohomology, we localize at a maximal ideal 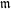$\mathfrak{m}$ of the Hecke algebra. We then prove a result of torsion freeness resting either on 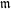$\mathfrak{m}$ itself or on the Galois representation 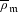$\overline{\unicode[STIX]{x1D70C}}_{\mathfrak{m}}$ associated to it. Concerning the torsion, in a rather restricted case than Caraiani and Scholze (« On the generic part of the cohomology of compact unitary Shimura varieties », Preprint, 2015), we prove that the torsion doesn’t give new Satake parameters systems by showing that each torsion cohomology class can be raised in the free part of the cohomology of a Igusa variety.

Lorsque le niveau en 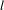$l$ d’une variété de Shimura de Kottwitz-Harris-Taylor n’est pas maximal, sa cohomologie à coefficients dans un 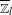$\overline{\mathbb{Z}}_{l}$-système local n’est en général pas libre. Afin d’obtenir des énoncés d’annulation de la torsion, on localise en un idéal maximal 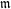$\mathfrak{m}$ de l’algèbre de Hecke. Nous prouvons alors un énoncé d’annulation de la torsion de ces localisés, reposant soit sur 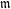$\mathfrak{m}$ directement, soit sur la représentation galoisienne 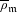$\overline{\unicode[STIX]{x1D70C}}_{\mathfrak{m}}$ qui lui est associée. En ce qui concerne la torsion, dans un cadre bien moins général que Caraiani et Scholze (« On the generic part of the cohomology of compact unitary Shimura varieties », Preprint, 2015), nous obtenons de même que la torsion ne fournit pas de nouveaux systèmes de paramètres de Satake, en prouvant que toute classe de torsion se relève dans la partie libre de la cohomologie d’une variété d’Igusa.

Keywords

classes de cohomologie de torsionvariété de Shimurafaisceau perversreprésentation automorphe

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F80: Galois representations 11F85: $p$-adic theory, local fields 11G18: Arithmetic aspects of modular and Shimura varieties 20C08: Hecke algebras and their representations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 3 , May 2019 , pp. 499 - 517
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

Beilinson, A. A., Bernstein, J. et Deligne, P., Faisceaux pervers, in Analysis and topology on singular spaces, I (Luminy, 1981), Astérisque, vol. 100, pp. 5–171 (Soc. Math. France, Paris, 1982).Google Scholar
Boyer, P., Monodromie du faisceau pervers des cycles évanescents de quelques variétés de Shimura simples, Invent. Math. 177 (2009), 239–280.Google Scholar
Boyer, P., Cohomologie des systèmes locaux de Harris-Taylor et applications, Compositio 146 (2010), 367–403.Google Scholar
Boyer, P., Filtrations de stratification de quelques variétés de Shimura simples, Bull. Soc. Math. France 142(fascicule 4) (2014), 777–814.Google Scholar
Boyer, P., Congruences automorphes et torsion dans la cohomologie d’un système local d’Harris-Taylor, Ann. Inst. Fourier (Grenoble) 65(4) (2015), 1669–1710.Google Scholar
Caraiani, A. et Scholze, P., On the generic part of the cohomology of compact unitary Shimura varieties, Preprint, 2015.Google Scholar
Emerton, M. et Gee, T., p-adic Hodge theoretic properties of étale cohomology with mod p coefficients, and the cohomology of Shimura varieties, Algebra Number Theory 9 (2015), 1035–1088.Google Scholar
Emerton, M., Gee, T. et Herzig, F., Weight cycling and Serre-type conjectures for unitary groups, Duke Math. J. 162(9) (2013), 1649–1722.Google Scholar
Harris, M. et Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, 151 (Princeton University Press, Princeton, NJ, 2001).Google Scholar
Herzig, F., The weight in a serre-type conjecture for tame n-dimensional Galois representations, Duke Math. J. 149(1) (2009), 37–116.Google Scholar
Ito, T., Hasse invariants for somme unitary Shimura varieties, Math. Forsch. Oberwolfach report 28/2005 (2005), 1565–1568.Google Scholar
Lan, K.-W. et Suh, J., Vanishing theorems for torsion automorphic sheaves on compact PEL-type Shimura varieties, Duke Math. 161 (2012), 951–1170.Google Scholar
Scholze, P., On torsion in the cohomology of locally symmetric varieties, Ann. of Math. (2) 182 (2015), 945–1066.Google Scholar
Suh, J., Plurigenera of general type surfaces in mixed characteristic, Compos. Math. 144(5) (2008), 1214–1226.Google Scholar
Wedhorn, T., Congruence relations on some Shimura varieties, J. Reine Angew. Math. 524 (2000), 43–71.Google Scholar