Information diffusion analysis: process, model, deployment, and application

Abstract

The information deployment on social networks through word-of-mouth spreading by online users has contributed well to forming opinions, social groups, and connections. This process of information deployment is known as information diffusion. Its process and models play a significant role in social network analysis. Seeing this importance, the present paper focuses on the process, model, deployment, and applications of information diffusion analysis. First, this article discusses the background of the diffusion process, such as process, components, and models. Next, information deployment in social networks and their application have been discussed. A comparative analysis of literature corresponding to applications like influence maximization, link prediction, and community detection is presented. A brief description of performative evaluation metrics is illustrated. Current research challenges and the future direction of information diffusion analysis regarding social network applications have been discussed. In addition, some open problems of information diffusion for social network analysis are also presented.

1. Introduction

In the digital era, social networks are gaining popularity and contributing to the information diffusion process. Therefore, analyzing the importance of social networks in information diffusion (Granovetter, 1973) is one of the focused areas of research among researchers. Users are not the only receivers of information these days; instead, they contribute largely to the evolution and propagation of information. The behavior of the individuals plays an essential role in the diffusion process as they participate in the exchange of information among peers and neighbors, defining their social relations and creating networks. This social network gradually grows as the topological relations of the users are covered, eventually leading to a large and complex network that can act as a medium for information diffusion. Social influence can be explained as a sort of behavioral change that is induced in an individual by another called an influencer. This change can be either knowingly/directly or unknowingly/indirectly (Chen et al., 2014). Factors like network distance, the strength of relationships among the individuals, characteristics of the individuals, timing, characteristics of the network, etc, are the factors that affect the level of social influence. The rapid growth and emergence of technology have increased the pace of information diffusion. Social media websites have contributed largely to the diffusion process as they are handy tools for spreading information faster. This leads to the need to analyze the influence and diffusion process through the available frameworks as sometimes it creates public issues, especially in cases like marketing and rumors related to emergencies (Razaque et al., 2019). The diffusion of information in social platforms is like the spread of an infectious disease (Abdullah & Wu, 2011). The situation of diffusion can be related to the rule of one percent, which highlights that mostly 1 $\%$ of the users contribute to the spread of the information largely, and the rest 99 $\%$ of the users have a nominal contribution in the propagation of the information (Hargittai & Walejko, 2008). Therefore, it is important to bring forth the existing theories and analyze the advantages and disadvantages of the existing models. Along with this, identify an apt social network information interaction design that can solve the problems induced by the evolution and diffusion of information. The four stages that help in analyzing information diffusion are: information diffusion process modeling (Varshney et al., 2014), influence evaluation (Varshney et al., 2017), algorithm design of SNA problems, and identification of influential users (Sheshar et al., 2021).

Digitalization has led to the generation of a tremendous amount of data through social networks because of user participation. This data contains a variety of information. People share details about the events happening in their daily lives, posting their opinions about breaking news, companies promoting their products by hiring influential users, etc. This way, the information propagates through the network and diffuses across the users (Chang et al., 2018). The connections of such users can further re-share the posts, and the process of diffusion continues. Users who propagate the information and users who adopt the information are called influencers and influenced, respectively. However, the information diffusion mechanism is unknown but analyzing the process of diffusion is important from the perspective of real-life applications like social recommendation (Elsweiler et al., 2007; Backstrom & Leskovec, 2011; Xu et al., 2014), viral marketing (Richardson & Domingos, 2002; Kempe et al., 2003; Leskovec, 2007), social recommendation (Elsweiler et al., 2007; Backstrom & Leskovec, 2011; Xu et al., 2014), social behavior prediction (Xu et al., 2016; Zhao et al., 2016; Ma et al., 2017), and community detection (Fortunato 2007, 2010). Therefore, studying information diffusion analysis for SNA is vital for enhancing scholarly discourse in the field. A potential research gap could be explored, focusing on developing a comprehensive framework that brings together different elements of information diffusion. This framework would encompass the processes, models, deployment strategies, and practical applications of information diffusion. Despite the extensive research on information diffusion, there seems to be a lack of a comprehensive approach that effectively addresses all the different components in a coherent manner. This manuscript aims to bridge the gap by thoroughly exploring and synthesizing the elements mentioned, providing valuable insights for both theoretical understanding and practical applications in various contexts. This has attracted several researchers from sociology, computer science, etc., to study the mechanism and propose models to simulate and describe the process. Some of these models include the linear threshold (LT) model (Granovetter, 1978; Girvan & Newman, 2002; Richardson & Domingos, 2002; Kempe et al., 2003; Leskovec, 2007; Fortunato, 2007, 2010; Xu et al., 2016; Zhao et al. 2016; Ma et al., 2017), independent cascade (IC) model (GoldenbergJ, 2002), and epidemic models (Kermack & McKendrick, 1932). Most of the models assume that the diffusion of information starts from a set of source nodes called seed nodes, and the other nodes can access the same through their neighbors. The influencers control the spread of information across the network, leading to influence maximization.

This article presents a review that studies about information diffusion analysis and its applications in various fields. The organization and contribution of the paper are illustrated in Figure 1. The main contribution of the study is given as follows.

1. 1. A brief discussion of information diffusion, component, and deployment is presented.

2. 2. The comparative analysis of classical diffusion models, along with their vulnerabilities, are discussed.

3. 3. Discussion of information diffusion analysis methods corresponding to different applications like community detection, influence maximization, and link prediction is presented.

4. 4. The performance evaluation measures, along with research challenges and future prospects regarding different applications, are detailed.

5. 5. The open problems are discussed, corresponding to information diffusion analysis.

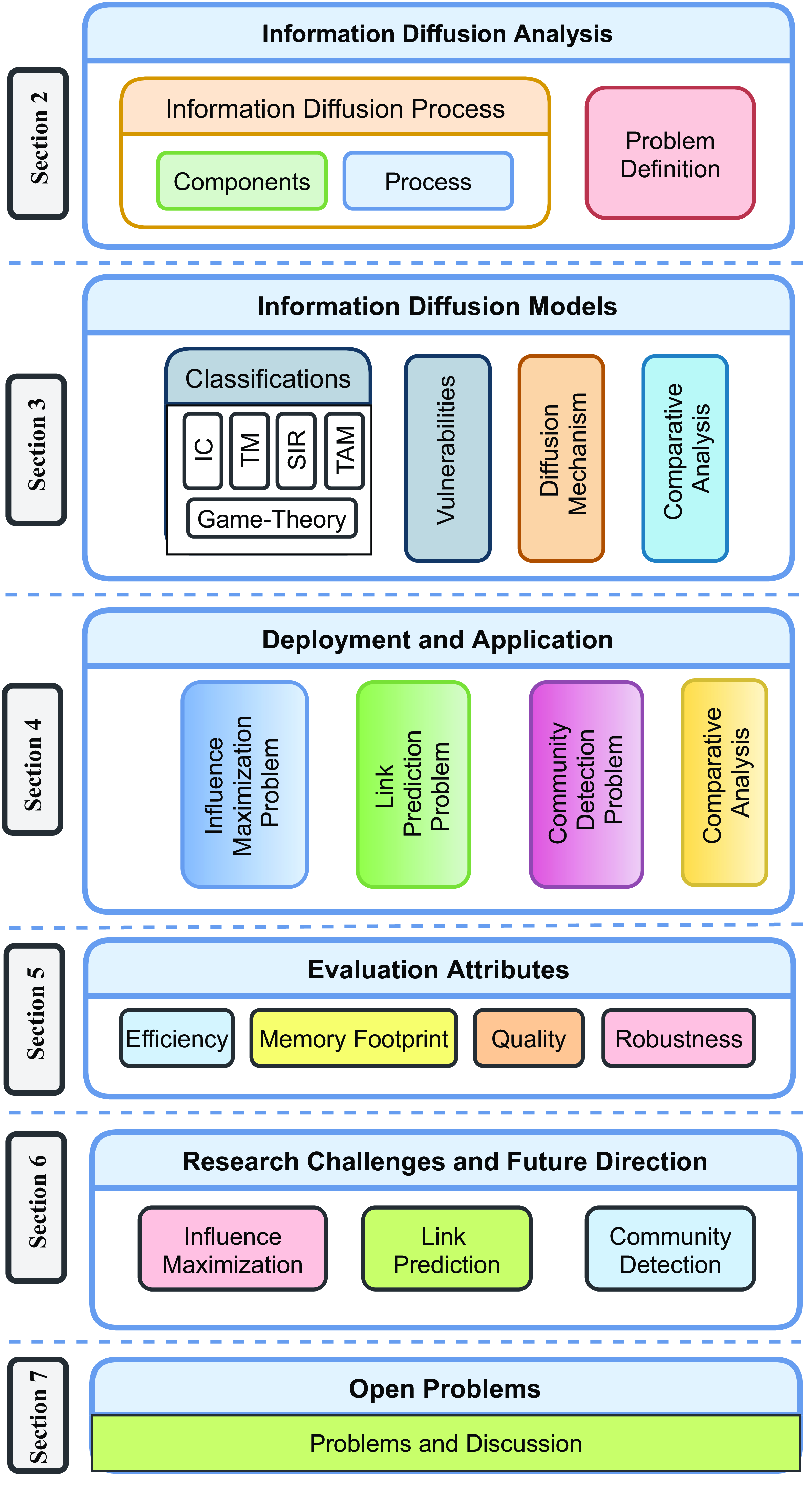
Figure 1. The information diffusion analysis survey overview

1.1. Difference from existing surveys

Several surveys exist in the literature that deal with influence maximization, diffusion models, link prediction approaches, etc. Each such survey focuses on some key points.

• • The authors in Das and Biswas (2021b) mainly focus on how information diffusion can be utilized for community detection. Different aspects have been covered in this survey like how the social facets and network properties are affected by the information flow, where the information is generated and how it is propagated in the network has been explored, how the different community detection algorithms are impacted by the network parameters and the social facets has been studied and also the evaluation metrics for quality and accuracy measurement of communities has been discussed.

• • In Kumar et al. (2020), a survey has been presented that explores the link prediction aspect of complex social networks. Several models have been discussed, including fuzzy models, network embedding methods, probabilistic methods, deep learning models, clustering-based models, etc. In this work, the aspect of different types of networks has also been considered like heterogeneous, temporal, and bipartite networks, and experimental results on real-world datasets have been discussed.

• • The authors of Azaouzi et al. (2021), presented a survey on influence maximization and their contributions include the exploration of influence maximization models based on node topologic technique, the impact of privacy preservation and security on these models have been studied, a survey has been done for the group-based models, and finally the open challenges and future directions have been depicted to lay down the foundation for further research.

• • Information diffusion models have been extensively studied and classified based on characteristics, and pertinent vulnerabilities, as well as threats, have been elaborated in Razaque et al. (2019). Applications and limitations of the models have been discussed, and recommendations have been provided for future improvement.

• • In Sheshar et al. (2021), authors have presented a survey of information diffusion models as well as influence maximization algorithms for single/multiple networks. In present survey covers the theoretical analysis of influence maximization techniques and their respective frameworks. It also covers the context-aware influence maximization approaches and performance metrics related to the influence maximization algorithms; their comparison and challenges have also been explored and depicted.

• • The authors of Singh et al. (2024, 2023) present surveys on social network analysis with respect to language information analysis, privacy, tools, SNA process, and application. They have also discussed the advantages and limitations of SNA techniques.

In this survey, Section 2 focuses on the information diffusion process, how it propagates through the network, affects the various parameters like network topology, social facets, etc., and impacts the various applications and users in the social networks. Section 3 discusses different types and aspects of the information diffusion models. Section 4 presents various research verticals such as influence maximization, community detection, and link prediction of SNA with respect to information diffusion. Section 5 discusses the evaluation metrics of SNA corresponding to various research verticals. Section 6 discusses research challenges and future directions, while Section 7 discusses open problems. Finally, Section 8 presents concluding remarks.

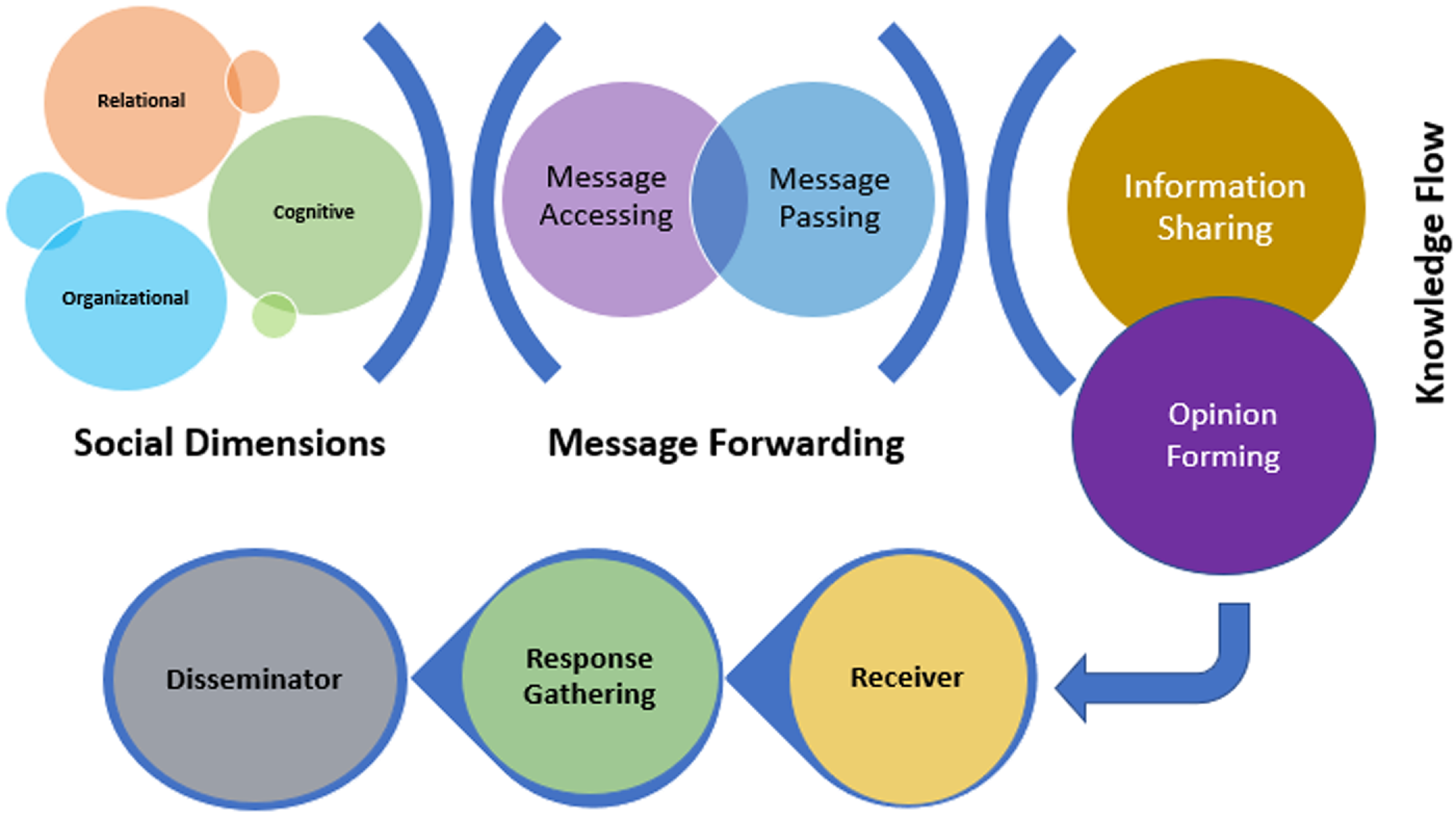
Figure 2. The information diffusion process components (Razaque et al., 2019)

2. Information diffusion process

Gaining a deep understanding of how information spreads is crucial in our modern, interconnected world. The rapid dissemination of information has a profound impact on shaping opinions, influencing behaviors, and driving societal trends. Nevertheless, despite its importance, there is a noticeable lack of research in fully examining the complexities of the information diffusion process. The manuscript seeks to explore the complex aspects of information diffusion. This manuscript aims to explain the fundamental processes that facilitate the spread of information across different platforms and networks. This research aims to provide valuable insights for scholars, practitioners, and policymakers by identifying key factors that influence the diffusion process, including network structure, content characteristics, and user behavior. In addition, the manuscript aims to provide practical applications and deployment strategies to bridge the gap between theoretical understanding and real-world implementation. This will help facilitate more effective information dissemination strategies in various contexts. The information diffusion process on social networks is affected by several factors. These factors can be analyzed considering three broad dimensions, namely cognitive dimension, structural dimension, and relational dimension:

• • Cognitive Dimension. The emphasis of this dimension is on common vision and understanding among the receivers of information, similar preferences of the users, etc. These commonalities affect the thought process of the entire circle of connections and lead to the spread of information as well as the establishment of interpersonal relations. This gives a chance to the user to judge and assess the value of the information and accordingly consume it (Bhattacherjee & Sanford, 2006).

• • Organizational Dimension. It consists of the network connections of an individual, flow of information, and resource pipeline access. It allows the users to access the information of their choice (Kim & Galliers, 2004).

• • Relational Dimension. It considers the details of the stable and long-lived connections that can lead to shorter paths for effective acquisition of information and further assure quality diffusion of information (Rajamma et al., 2011).

Further, concerning each of these dimensions, there are several components that affect the information diffusion and should be considered in the analysis of the process (Razaque et al., 2019) as shown in Figure 2.

• • Message Access. It consists of a platform that allows the users to access diffused messages, and this platform further forwards the messages that are received to the neighbors. Later, the message is received by all the nodes in the network, which increases the overhead of some needless messages but leads to a very vigorous distribution of the information (Khelil et al., 2002).

• • Trust, Reciprocity and Cooperation. In a social network, both the receiver and the disseminator are connected based on trust; sharing and reciprocation of information happens based on the status of personal relations, and sometimes, the users choose to cooperate among themselves to gain access to more messages and gather more information (Manapat & Rand, 2012).

• • Value. In a network, the existence of multiple connections leads to excellent quality and a large amount of knowledge dissemination through information circulation. The recipients can further evaluate the information based on the value and usage of information that solely depends on the needs, choices, and experiences of the users (Guille et al., 2013).

• • Network Link. The links in the networks allow the users to share their views, make the level of knowledge and values more balanced so that the information can be popularized, and the breadth of diffusion can be expanded so that more and more receivers can get access to it.

• • User Information. It can be obtained from YouTube, social sites, blogs, etc. This information highlights the role of social connections in information gathering and how information diffusion impacts the choice of one user based on the preferences of other connections (Susarla et al., 2012).

• • Individual Behavior. Once the receiver gets access to the messages, they can filter out the useful information that matches their requirements, preferences, and values.

• • Feedback and Resource Sharing. The information diffusion process gives a fair chance to the receiver to exchange views and feedback about the information with the disseminator and also share other resources (Greenhalgh et al., 2008).

2.1. Information deployment

In social networks, communities’ formation and detection depend on several factors like network attributes, temporal characteristics, and social attributes. The data stream in the organization influences every one of these variables contrastingly at various levels. In this manner, it is fascinating to see what the data stream means for local area recognition and informal communities. The elements influencing the informal communities can be extensively delegated (Das & Biswas, 2021b):

1. 1. Network Properties. Topological and structural characteristics of the network.

   • • Edge Strength Measures. These measures, like connection strength, value strength, and tie strength, are used to assess the relationship between two vertices that share a common edge. The strength, however, can be measured by computing the number and the type of vertices impacted by the diffusion process.

   • • Belongingness Measures. For any vertex v, the belongingness in a specific local area c is controlled by having a place degree or having a place factor. Thinking about the viewpoint of data dissemination, the belongingness strength can be estimated by deciding the kind of vertices impacted during dispersion.

   • • Centrality Measures. The increasing popularity of social networks has led to an increase in the amount of information that is generated and made available to users. However, the ideas absorbed by the individuals highly depend on certain influential entities that can activate the inactive vertices through their influence. Such entities control the propagation of information in the network to a great extent and enhance the rate of diffusion. Some of the measures for identifying influential entities include betweenness centrality, degree centrality, and closeness centrality.

   • • Clustering Coefficient. During the time spent on data dissemination, the data is proliferated across the organization through the innate vertices that are available in the base conceivable length. Simultaneously, some topological properties of the organization are taken advantage of during the dissemination interaction. One such property is the grouping coefficient, which decides the degree to which the vertices bunch together and contribute fundamentally to local area identification.

   • • Structural Equivalence. Part of data is accessible in interpersonal organizations nowadays, yet while getting the data, the dependability of the data assumes a significant part for the client. Here impact makes an effect, that is, the data spread directed by the impact is more dependable and arrives at a bigger arrangement of vertices. Such an impact can be addressed by data not really set in stone from client credits, client demands, and other pertinent elements. The features that can measure the information diffusion probability by utilizing appropriate similarity/dissimilarity evaluation techniques. Thus, these methods are used to evaluate the structural equivalence. Structural equivalence measures include the Jaccard coefficient, cosine similarity, and Euclidean distance.

   • • Boundary Vertex. Users in social networks connect with other users who are either similar or known to them. Hence, the information propagation in the network is either controlled by the similarity or by the topology. In terms of topology, the extent to which the neighboring nodes tend to connect. Concerning similarity, it is the user’s attribute, interest, or characteristic that controls the connections. The diffusion of information in the network sometimes affects a pair of vertices differently as they may be exposed to two types of information that are different from each other. Such neighboring vertices of a vertex are referred to as boundary vertex.

2. 2. Social Facets. It quantifies the various aspects of social interaction.

   • • Contagion. In social networks, following a particular trend, is a usual practice. Hence, any activity of a user is affected by the neighbors’ actions. The inactive vertices get activated by the neighboring vertices during the information diffusion process. This influence of neighbors on the inactive vertex is called contagion. A higher degree of the vertex indicates higher chances of getting affected by the information propagated by the neighbors and vice versa.

   • • Common Neighbors. Formation of groups based on some similarity is a common characteristic of social networks. These groups exchange information during the process of diffusion. It is observed that there is a strong relationship among those users who have a huge number of common neighbors. Therefore, a dense sub-graph can depict the diffusion outcomes in such cases, and the community detection algorithms can utilize this facet to recognize inherent communities.

   • • Topic. Interest in the group and the dynamics of the diffusion network highly affect the speed at which the diffusion of a topic happens in a social network. For example, a politically inclined group will be affected more by a political campaign and will not be bothered about the advertisement of trekking equipment. A high diffusion speed indicates a higher affinity for that topic in the underlying network.

   • • Homophily. The users in social networks tend to connect with like-minded or similar users. This similarity is termed homophily which is exploited during the information diffusion process. The interaction pattern between similar users can be modeled through the independent cascade model. It is assumed that the diffusion initiated based on homophily affects many homophilic connections.

   • • Social Interaction Channels. Nowadays, users spend quite some time on social networks to interact with their peers and friends. Much information exchange happens on social networks, which opens up a kind of interaction channel through which people staying at physically different locations can also interact. This enhances and broadens the information diffusion process and increases the efficiency of the interaction channels.

   • • Influential Spreaders. Certain entities are popular enough and have one too many relations in the network. Such users are referred to as influential spreaders as they can initiate information diffusion in social networks by activating inactive users. However, the strength of information propagation depends upon the data (whether it meets the user’s requirement) and the popularity of the spreader in the network. The higher the impact of the influential spreader, the higher the probability of diffusion.

3. Information diffusion models

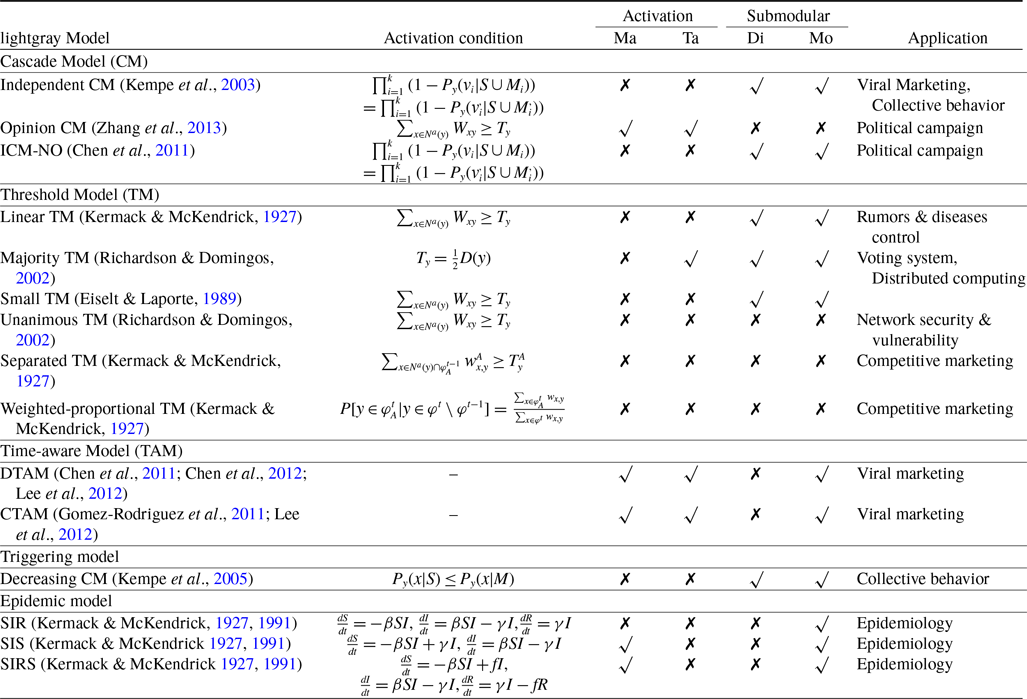
This manuscript highlights the significance of information diffusion models in understanding SNA analysis. These models are extremely useful for researchers, allowing them to analyze how information spreads across different platforms and communities. By understanding the inner workings and patterns of information spread, these models help in creating better strategies for communication, marketing, and policy-making. In addition, they enable individuals and organizations to navigate the intricacies of the digital era, promoting well-informed decision-making and strengthening societal resilience. Therefore, the investigation and improvement of information diffusion models are crucial pursuits that contribute to a deeper comprehension of our information-driven world. Information diffusion models have an essential role in several real-life applications, including sociology, ethnography, and epidemiology. The main components of the information diffusion model are disseminator, resource sharing, receiver, and opinion formation (Sheshar et al., 2021). We have discussed the classical diffusion models in the following section and summarized the characteristics in Table 1.

• • Threshold Model (TM). In the TM, or then again set of edge esteems, is utilized to separate scopes of qualities for the conduct anticipated by the model (Schelling, 2006). Straight limit model (LTM) is the most famous edge dispersion The linear threshold model (LTM) is one of the most popular threshold diffusion models where a node becomes active if the influence of the neighbors is greater than a defined threshold. In LTM, the threshold always follows uniform distribution over [0,1]. One of the modified TMs is a linear threshold with color that considers the client’s involvement in an item and catches item reception instead of affecting (Bhagat et al., 2012). Direct TM is additionally altered to deal with the assessment change of clients and permits them to change among dynamic and latent states (Pathak et al., 2010).

• • Cascade Model (CM). In CM, if a node becomes active at one point in time, it has the same probability of activating its inactive neighbors at the next timestamp (Goldenberg et al., 2001). As the cascading process continues, an already active node will never become inactive in the future. The other variations of independent CM (ICM) are ICM with negative opinion (Chen et al., 2011) or ICM with positive and negative opinion (Nazemian & Taghiyareh, 2012).

• • Time-aware Model (TAM). In some engendering models, the spread of social impact has been amplified explicitly to a decent time frame. These are known as TAM, where the intermingling of proliferation relies upon the period rather than the number of cycles (Chen et al., 2012). The model is acquainted with accomplishing time-basic interest. TM can be isolated into two sub-classes which are a discrete-time model and a ceaseless time model (Rodriguez et al., 2011).

• • Triggering Model (TRM). TRM is the blend of TM and CM. In the TRM, every hub is related to an edge esteem and an appropriation work. A selection of its neighbors is guided by the characterized work with a similar likelihood (Kempe et al., 2003). This model freely chooses an irregular subset of its neighbors in each occurrence of the dissemination interaction (Kempe et al., 2005).

• • Epidemic Model (EM). The decent individuals can be divided into three classes in an epidemic model: helpless (S), irresistible (I), and recuperated(R). Three plague models are generally utilized which incorporate defenseless irresistible recuperated (SIR) (Schütz et al., 2008), powerless irresistible helpless (SIS) (Parshani et al., 2010), and vulnerable irresistible recuperated defenseless (SIRS) (Magal & Ruan, 2014). This scourge model proliferates the data dependent on the strength of the neighbors.

• • Game Theory Model (GTM). In GTM, individual conduct systems are depicted in harmony by examining the practices and advantages of every member (Easley et al., 2012; Jiang et al., 2014). In this model, the players make a choice and pay off to every player dependent on the choice made by all of the playing players (Muhuri et al., 2018).

Table 1. The comparison of the diffusion models characteristics (Singh et al., 2019; Singh et al., 2021), where Ma=Multiple Activation, Ta=Time-specific Activation, Di=Diminishing Returns, Mo=Monotone

3.1. Information diffusion vulnerabilities

Information diffusion models can face many vulnerabilities if the common weaknesses are uncontrolled. As with the consistent advancement of networks over organizations, social media, etc., online protection has become a significant subject. Vulnerabilities of Information Diffusion mainly depend upon the model applied for link prediction. Some of the common vulnerabilities of Information Diffusion models are discussed below:

• • Node Paralysis. A lot of exploration is directed at node paralysis of motion in various models proposed in state-of-the-art approaches (Razaque et al., 2019). A one-dimensional model begins with a random initial state. The intermittent limit conditions are dependent on different models. The likelihood of the resistance is 0.5, a big part of the endorsement and half resistance. Under various boundaries, the likelihood of developing the last attractors of ferromagnetism is likewise unique. The likelihood that the attractor gives up at a similar starting thickness fluctuates with the collection file. Under a similar collection file, the more noteworthy the likelihood of a similar beginning thickness keeps an eye on the attractor when the association likelihood becomes bigger; the expansion of the association likelihood will make the framework bound to look steady. When the accumulation record expands, something similar starting thickness will generally be more noteworthy in the likelihood of the attractor (i.e., the framework is bound to look reliable because of the expansion in the number of short-range associations). Such different circumstances prompt Vulnerabilities.

• • Continuously Changing.: The organization is in an implicit, persistent way. The method involved with adding additional associations proceeds until the number of huge distance affiliations and the number of short distance affiliations (i.e., affiliation probability) shows up at a particular worth. Like this, the typical neighbor number of each center point in the little world organization is $4(1 + x)$ . At the point when the amassing record (T) reaches 0, the theory of the little world organization has transformed into a little world association. Regardless, with T1, there are incredibly close center points. Such extraordinary minimal world associations are relative to standard associations. At the point when 0 $\le $ T $\le$ 3, because of the characteristics of extra-critical distance affiliations, this reach has rich characteristics. In any case, it creates a shortcoming that can be the justification for the attack (Razaque et al., 2019).

• • Instability. Instability in the model significantly reduces the efficiency and performance of the model. Given the Instability of network geography, deciding the impact of joining and leaving the host is essential, particularly in a P2P organization. To more readily comprehend the effect of entering and leaving on the transmission of dynamic worms, the proportion of the pestilence and irresistible infection boundaries ought to be utilized. The aftereffects of several models show that the expansion and flight of hosts significantly affect the notoriety and spread execution of the topology-aware dynamic worms (Razaque et al., 2019).

• • Harder Node Evaluation. To control the diffusion of viruses, certain models combine the minimum traffic with the time Markov chain features. One such model is the SIR model, wherein the infection and its removal can be described through this vulnerability. The traffic flow is affected in the congestion and free flow phases by the viral transmission, and to assess its dynamics, models like SIR may be used. The goal is to identify the effect on the traffic conditions and dynamics of the system due to virus diffusion, that is, in the congestion and free flow stages (Razaque et al., 2019).

• • Limited Size. In social networks, limited size is one of the vulnerabilities. It can be studied considering the network construction. The complex process of the experimental methods leads to large size. Also, the data sets that are compiled are of varying and considerable sizes. The data that is obtained from multiple sources have sufficient subjective biases which is not compatible with existing social network size. However, this issue can be tackled by using the affiliation network as performed in the SIR model to study the state of the nodes in the network.

• • Data Reduction. In Serban et al. (2016), the authors have suggested that, in general, the distance between the source of every estimator and its closest tree network is constant. The number of sources can be estimated using the proposed algorithm, even if the real and existing sources are unknown. Collisions between the wireless intermediate nodes and transmission signals lead to a reduction in the throughput of end-to-end data transmission. Therefore, in certain models like SIR, there are increased chances of inviting vulnerabilities due to this reduction.

• • Abhorrent Types. It is difficult to assess the authenticity and truth value of the information flowing through social networks. When the information arrives at a node, it is the choice of the netizen whether he/she wants to forward it or not. Similarly, sending real or distorted information to the disseminator is also the choice of the netizen. The multi-agent and game theory concepts can well describe both situations, and it is utilized in the background to study the information dissemination in the networks. The model of Anshuman et al. (Chhabra et al., 2017) can be explored to identify the communication behavior of online users connected through social networks.

• • Independence of Values. Based on the user’s awareness of security, their behavior is affected. The quantifying factors for these behavioral changes have been analyzed by studying the propagation mechanism of the worms in the social networks (Seddiki & Frikha, 2012). The information transmission for multi-layer online networks follows the mechanism of information dissemination in social networks. This model is based on the idea of the evolutionary game model that is used in the information diffusion process established between government bodies and netizens. For example, the strategies executed by the government to control the harmful network group events that negatively impact the social order have been proven to be very effective.

4. Information diffusion deployment and application

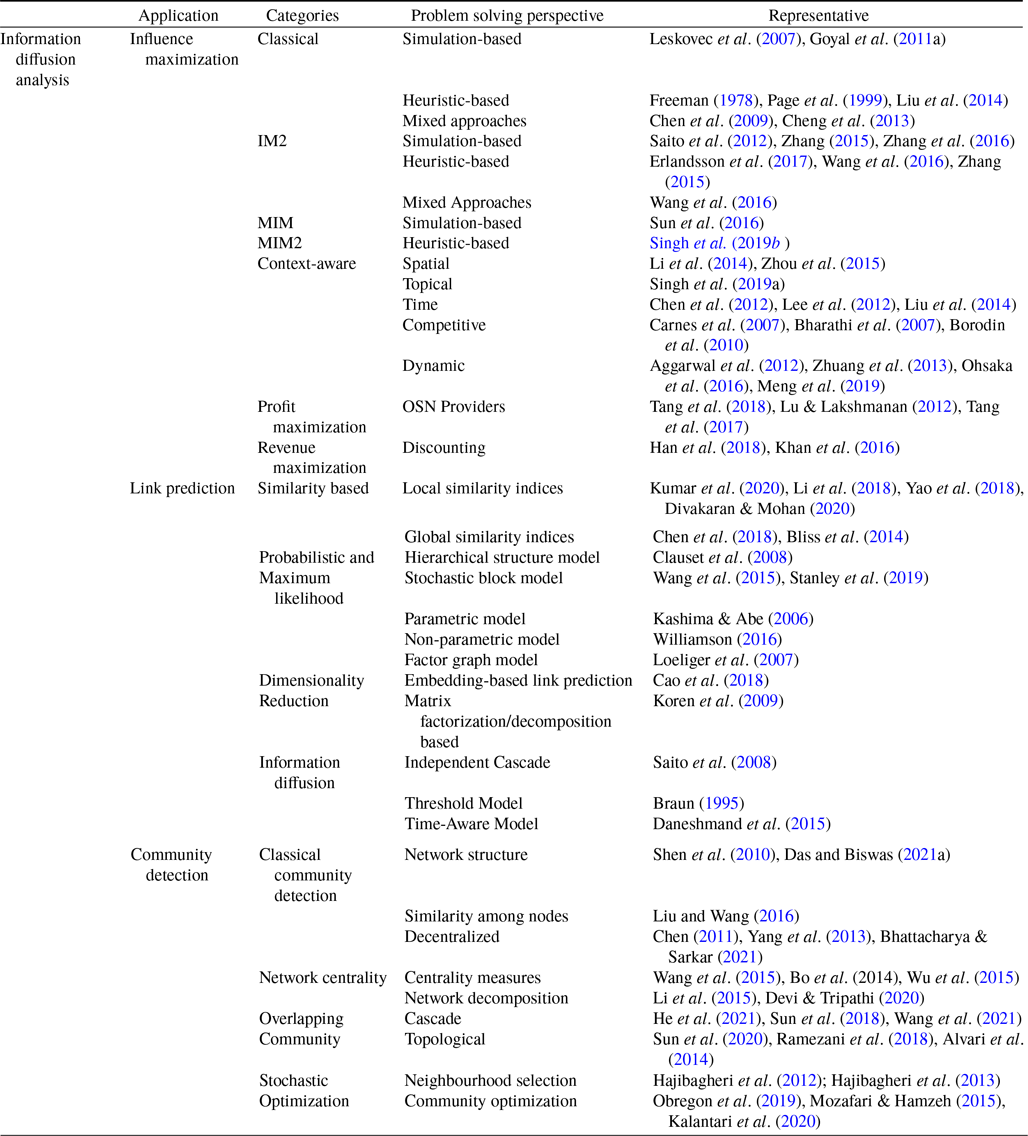
Online engagement and interaction of users over social networks have attracted researchers to solve real-world problems such as rumor control, viral marketing, recruitment, and social recommendation by utilizing information flow analysis. The topological information and social facets have been used to analyze the information flow over the network. Therefore, researchers in recent years have shifted focus to information diffusion analysis for finding solutions for influence maximization, community detection, and link prediction. This section is devoted to analyzing the role of information dissemination for link prediction, influence maximization, and community detection problem-solving.

Table 2. Illustration of information diffusion analysis over different applications (Kumar et al., 2020; Singh et al., 2021; Das & Biswas, 2021b)

4.1. Influence maximization

Identification of influential word-of-mouth promoters is a challenge in influence maximization (IM), which aims to increase product uptake. Kempe et al. (2003) was the first to present an optimization model for the IM problem under the linear threshold and independent cascade models of classical diffusion. They have proposed a simulation-based greedy solution to identify seed users with an approximation guarantee $1-1/e-\epsilon$ . The greedy algorithm utilizes the information diffusion capacity of each individual in the network to evaluate the user’s influence spread. The algorithm finds influential seeds iteratively to avoid overlapping avoidance. The main limitation of the greedy solution is its time efficiency due to the time-consuming Monte Carlo (MC) simulation. It is because of the stochastic nature of the diffusion process that a new set of users is activated at each iteration. The influence maximization algorithms have been categorized based on the context of the product, and network (Singh et al., 2021) as shown in Table 2. The basic framework of an influence maximization algorithm is depicted in Figure 3 (Arora et al., 2017; Singh et al., 2021). The first component experimental setup of the IM framework configures the diffusion process with influence and activation probabilities. The seed selection process identifies the seed users corresponding to the seeding strategy and diffusion model. Finally, the algorithm’s performance is evaluated regarding influence spread and efficiency. The characteristic summary of the influence maximization method is present in Table 2.

Table 3. The comparison of influence maximization algorithm based on information dissemination model (Singh et al., 2021)

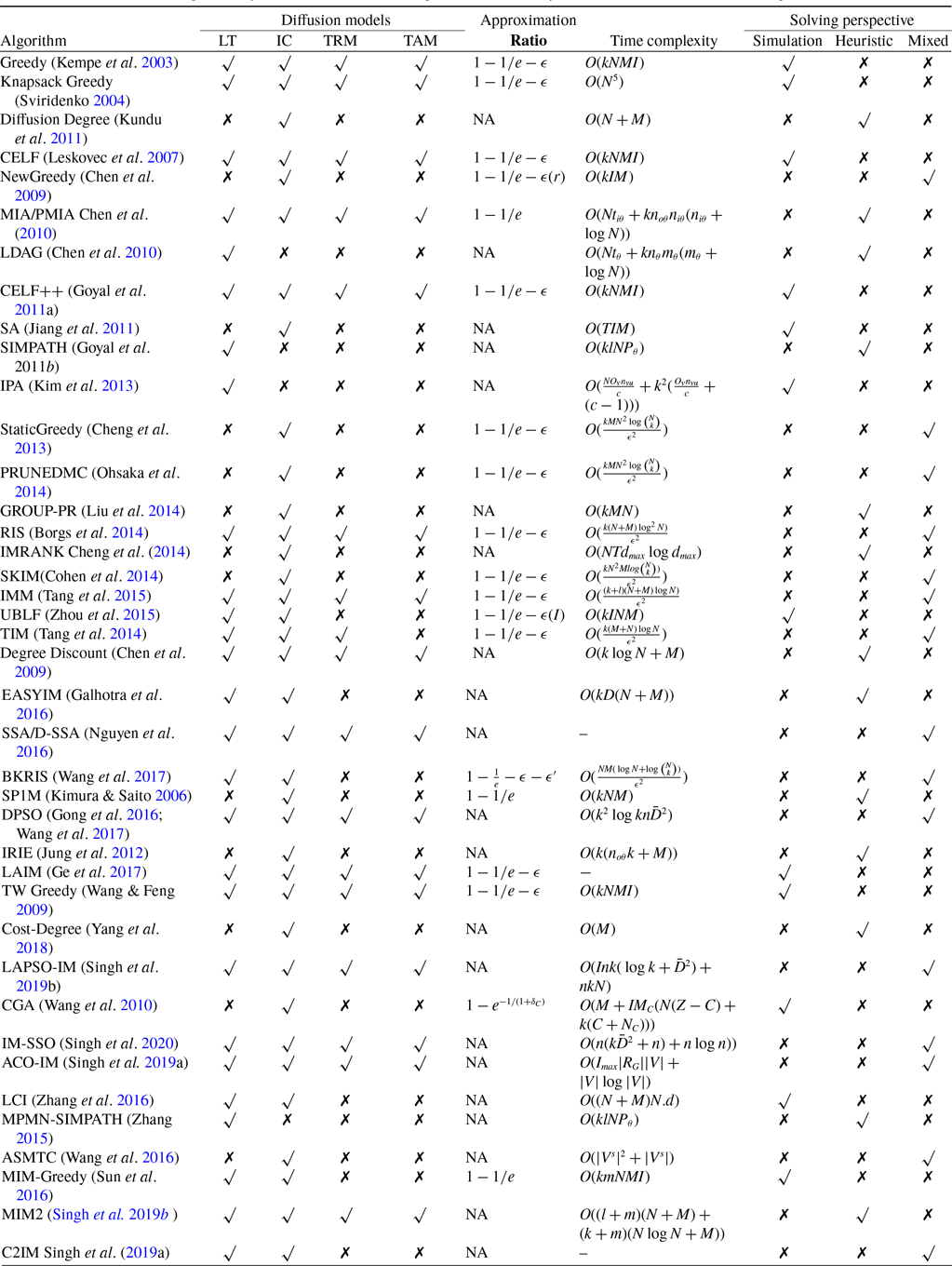
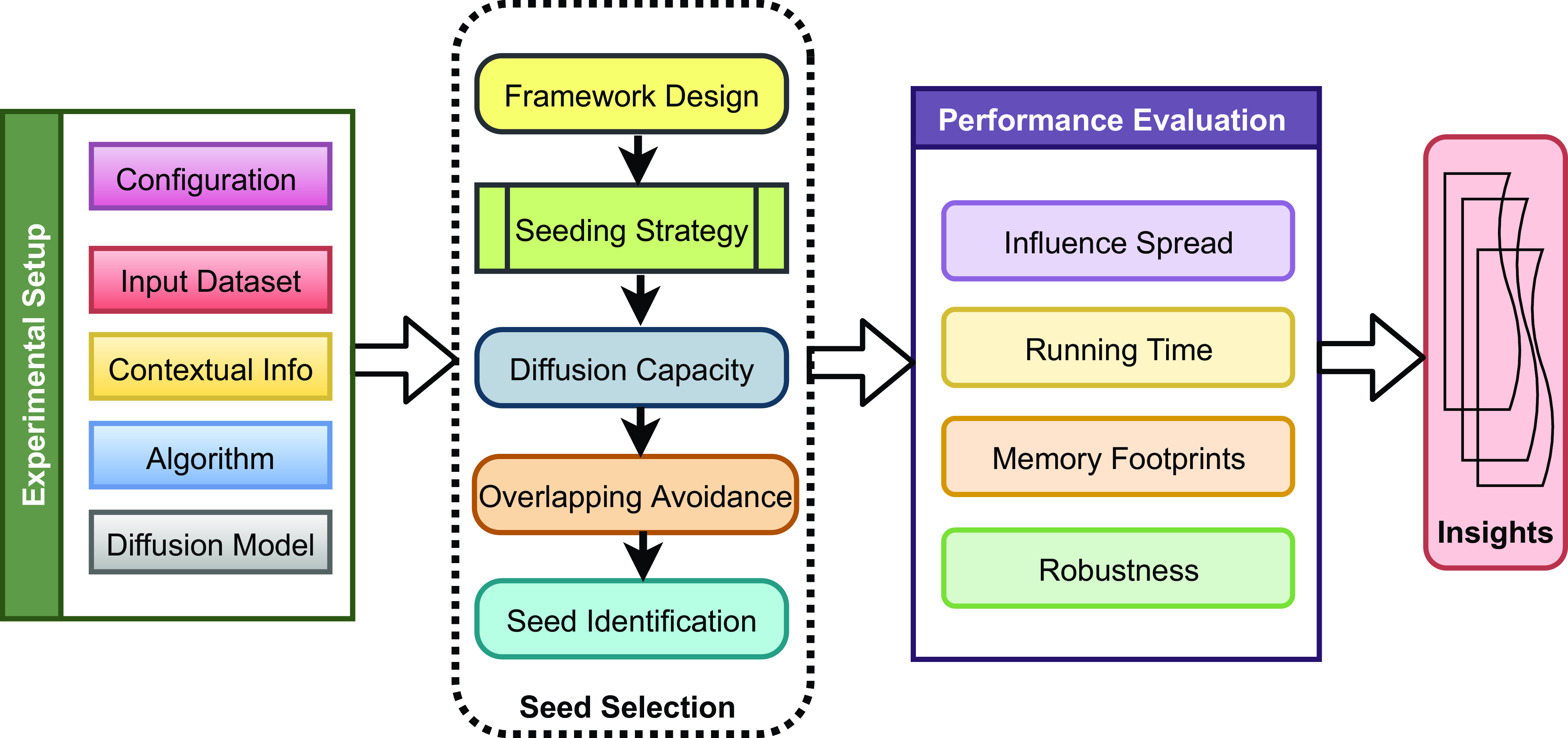
Figure 3. The influence maximization framework under information diffusion model (Singh et al., 2021)

4.1.1. Classical influence maximization

The authors of Sviridenko (2004) modified the IM problem by introducing individual node price constraints, which was unitary in Kempe et al. (2003). The greedy solution is not scalable and computationally efficient for large-scale networks. Therefore, much research is devoted to computing effective and efficient solutions for the IM problem. Three types of solutions exist in literature to tackle classical IM problems; simulation-based, heuristics, and mixed approaches. The heuristic-based methods do not guarantee approximation while simulation and mixed approaches have. By utilizing the submodular property to reduce the amount of MC simulations on the greedy algorithm, Leskovec et al. (2007) offer a simulation-based method known as cost-effective lazy forward (CELF). The influence evaluation function under IC and LT models is submodular as proved by Kempe et al. (2003). Therefore, Leskovec et al. applied submodularity to the greedy algorithm for iterative computation of seed nodes based on individual influence, significantly decreasing the number of MC simulations. The CELF is almost 700 times more efficient than the greedy method. The further optimization of the CELF method is presented by Goyal et al. (2011a) and is known as CELF++. CELF++ utilizes the marginal influence gain of each individual in previous and current iterations to avoid unnecessary MC simulations. This method also uses traditional diffusion models LT and IC to estimate the marginal influence gain of an individual. CELF++ is 30–50 $\%$ faster than CELF.

Some works focused on improving the time complexity of MC simulations rather than reducing MC simulations. The authors of Wang et al. (2010) present a community-inspired greedy solution known as CGA. This algorithm divides the network into subnetworks to identify seed users without overlapping influence. Therefore, it significantly reduces the search space, which improves the time complexity of MC simulations. However, because of the complexity associated with community identification, CGA is not ideal for large-scale networks. Because there are more MC simulations, it has been shown that simulation-based methods are not practical for large-scale networks. By giving each person an approximative score, certain heuristic approaches have been developed to increase scalability. This scoring or ranking is done by features like information diffusion, centrality, topological information, etc., to identify seed nodes. There are some efforts (Page et al., 1999; Jung et al., 2012; Liu et al., 2014) have been made in this direction.

4.1.2. Influence maximization across multiple networks (IM2)

The classical IM methods consider a single type of relationship and networks to estimate users’ influence while avoiding a scenario where users engage in multiple networks simultaneously. Considering simultaneous engagement of users across networks leads to a new framework of IM known as influence maximization across multiple networks (IM2). The authors of Zhang (2015) introduce a multi-phase multilayer network-based framework to identify influential users by utilizing SIMPATH (Goyal et al., 2011b) and CELF++ (Goyal et al., 2011a) algorithms. Zhang et al. adopt traditional diffusion models IC and LT to propagate influence across layers with different influence probability assignments. A new modified greedy algorithm is presented for the IM2 framework by utilizing lossless and lossy coupling strategies (Nguyen et al. 2013; Zhang et al., 2016). The authors of Wang et al. (2016) introduced an IM algorithm known as agent selection problem (ASP) under IM2 and distributed settings. ASP considers a multilayer framework for seed selection in mobile ad-hoc networks.

4.1.3. Multiple Influence Maximization (MIM)

Most of the literature focuses on the IM scenario with only one product for marketing. However, some work considers competitive product marketing but not for non-competitive distinct product adoption. Based on the presumption that people have the purchasing power to accept many products at once, Sun et al. (2016) have presented a MIM greedy algorithm. They improved the time efficiency of greedy under the IC diffusion model by using the influence evaluation function’s submodular characteristic. MIM framework first constructs different product diffusion graphs by the IC model. Then it identifies influential users for each product corresponding to product diffusion graphs. Finally, select seed nodes across diffusion graphs iteratively. The MIM greedy ensures $(1-\frac{1}{e})$ approximation guarantee.

4.1.4. Multiple Influence Maximization across multiple networks (MIM2)

The MIM2 framework considers multiple non-competitive products and multiple relationship networks simultaneously to maximize product adoption. Therefore, the product diffusion graph construction and network coupling will be the key functionality under this framework. Singh et al. (2019b ) were the first to introduce a heuristic-based MIM2 algorithm to identify seed nodes by back-propagation. MIM2 first performs network coupling based on overlapping users and topological structures. Then it creates product diffusion graphs corresponding to each product from the coupled multiplex network. The following influential users are identified for each diffusion graph. Finally, seed nodes are selected across different products to maximize product adoption under traditional diffusion models.

4.1.5. Context-aware influence maximization

Most of the conventional IM approaches focus on the topological information of the network and avoid some critical factors like product information, target audience, contextual and semantic information, and geographical information. It was observed that conventional IM approaches are ineffective in real-world scenarios. Therefore, some researchers started focusing on context-aware IM solutions in recent years to improve the effectiveness of seed users. Some of the topic-relevant approaches such as LGA/ELGA (Guo et al., 2013), IMIP/IMAX (Lee & Chung, 2015), CTVM (Nguyen et al., 2016), MFIP (Li et al., 2020) focus on the users interest to a different topic for the diffusion process. This will help to identify seed users from product-specific audiences. The authors of Singh et al. (2019a) proposed a context-aware community-based influence maximization (C2IM) algorithm that utilizes the topic-dependent contextual diffusion models to propagate influence. C2IM considers community and topical information to improve the efficiency and effectiveness of the seeding strategy. The seed strategy under C2IM estimates the diffusion degree by back-propagation of influence from non-desirable nodes. The diffusion degree works as a ranking method for seed selection.

4.1.6. Profit maximization

Profit maximization (PM) extends the classical IM problem, which considers actual product adoption rather than social influence. Profit maximization integrates the costs of advertisers and network service providers. There are some efforts (Lu & Lakshmanan, 2012; Tang et al., 2017; Li et al. 2017; Tang et al., 2018; Weersink & Fulton, 2020) have been made in this direction. The authors of Lu and Lakshmanan (2012) utilize the extension of traditional diffusion models to estimate actual product adoption over social influence. The traditional diffusion models IC and LT are modified by adopting new states and active and inactive states. These states help to compute actual product adoption, which drives profit and revenue computation. The authors also proved that the profit function is submodular under these diffusion models.

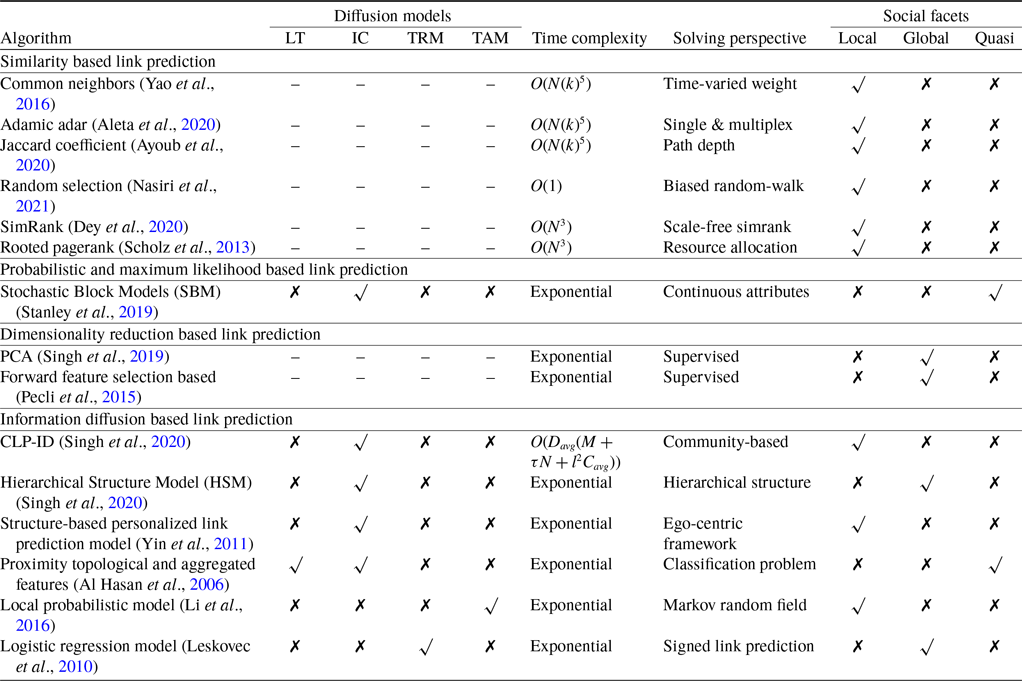
Table 4. The comparison of link prediction algorithm based on information dissemination model (Kumar et al., 2020)

4.2. Link prediction

Link prediction (LP) (Singh et al., 2022; Mishra et al., 2022; Singh et al., 2024) licenses to gather absent or future associations in an organization are termed Link Prediction. The organization association characterizes how data spreads through the hubs. Thus, the spreading might actuate changes in the associations and accelerate the organization’s development. The development of web-based media has drawn little consideration from specialists and organizations. New stages are ceaselessly arising, for example, Facebook and Flickr (2004), YouTube (2005), Twitter (2006), and Miniature blog (2009), among others. Given the significance of various spaces and regions, research points, for example, Connection Prediction (LP). Furthermore, data diffusion has gotten considerable consideration in perplexing social network regions during the last few years. Notwithstanding, they are points, for the most part, examined in isolation, even though their outcomes are applied in comparative areas, such as viral promoting, political missions, and business process displaying.

The issue of suggesting joins has a few applications, such as recommending absent and likely associations in cloud data or, on the other hand, robust hub identification. Specifically, the expectation of future connections is helpful in comprehending the organization and correspondence evolution. For instance, in web-based media stages, promising associations that do not exist yet can advance commitment and collaboration among users, influencing the organization structure. Thus, the organizational structure impacts the correspondence or the spread of data. The link prediction working framework is shown in Figure 4.

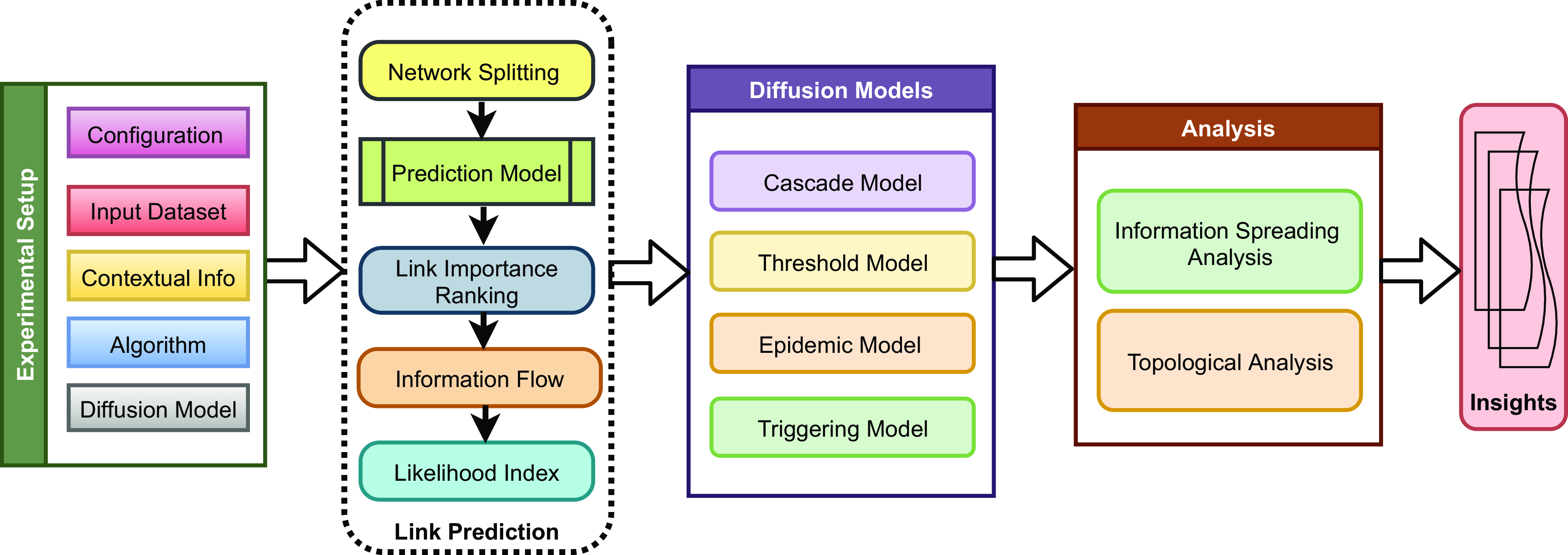
Figure 4. The link prediction framework under information diffusion model (Kumar et al., 2020)

LP techniques gauge the new edges as indicated by some association systems, similar to the distance and briefest ways among hubs, the triangles or Triassic conclusion, and the likeness with shared neighbors, among others. These primary components are fundamental in deciphering network development. For instance, renowned and persuasive clients will generally acquire associations, making traffic-based alternate ways and working on the productivity of data spreading on the network. Thus, investigating the dispersion interaction can assist with understanding the effect of clients’ cooperation, for example, what re-posting a message means for the spread of images, recordings, or fake news (bits of hearsay) on the networks. Clients in web-based interpersonal organizations make new companions and look for and share data. When a client shares a message, his/her contacts can be affected to re-post that data, driven by the homophily property that creates a diffusion cycle. Link Prediction Approaches are broadly categorized into:

• • Similarity-based Approaches

• • Probabilistic and Maximum Likelihood-based Approaches

• • Dimensionality Reduction-based Approaches

• • Information Diffusion-based Link Prediction

4.2.1. Similarity-based approaches

Interface expectation relies on similarity-based measurements, in which a comparability score S(x,y) i is calculated for each pair x and y. The score S(x,y) can be calculated by considering the underlying or hub properties of the thought-about pair. The joins that are not noticed (i.e., $U-E T$ ) are assigned scores based on their similarity. Centers with a higher score are more likely to have the expected association. The resemblance measures between each pair are still up in the air using a couple of properties of the association, one of which is an essential property. Scores subject to this property can be assembled in a couple of classes like area and around the world, center ward and way dependent, limit ward and limit free, and so forth.

1. 1. Local Similarity Indices. Nearby records are, for the most part, determined utilizing data about normal neighbors and hub degrees. These files think about quick neighbors of a hub. Instances of such files contain normal neighbors, special connections, Adamic/Adar, asset distribution, etc (Lü et al., 2009). A few of the popular local similarity approaches are discussed in the following section:

   • • Common Neighbors (CN). In a given association or graph, the size of common neighbors for a given pair of center points x and still up in the pair as the size of the combination of the two center regions.

   • • Preferential Attachment (PA). The possibility of a particular connection is applied to create a developing sans-scale network. The term developing addresses the steady idea of hubs over the long run in the organization. The probability augmenting new association related with a hub x corresponds to k $\_$ x, the level of the hub.

   • • CAR based Common Neighbor Index (CAR). Car setup documents are presented based on the assumption that the interface presence between two center points is additionally plausible in the event that their ordinary neighbors are people from a close by (neighborhood (LCP) speculation).

   • • Local Naive Bayes-based Common Neighbors (LNBCN). This strategy depends on the Guileless Bayes’s hypothesis and contentions that diverse ordinary neighbors assume a distinctive part in the organization and contribute contrastingly to the score work processed for non-noticed hub sets.

   • • Node Clustering Coefficient (CCLP). This record is also based on the organization’s grouping coefficient property, which registers and adds the bunching coefficients of a seed hub pair’s relative abundance of normal neighbors to determine the pair’s most recent closeness score.

2. 2. Global Similarity Indices. Global files are processed utilizing the whole topological data of an organization. The computational intricacies of such techniques are termed global similarity indices. These have higher time complexity and appear to be infeasible for enormous organizations. Some of the common Global Similarity Indices approaches are discussed below

   • • Katz Index. it can be considered as a variation of the briefest way metric. It straightforwardly totals over each of the ways among x and y and dumps dramatically for longer ways to punish them (Katz, 1953).

   • • Leicht–Holme–Newman Global Index (LHNG). This overall record relies upon the standard that two centers are similar if the two of them have a speedy neighbor, which resembles the other center point. This is a recursive importance of closeness where an end condition is required. The end condition is introduced similarly to self-closeness, that is, a center is such as itself (Leicht et al., 2006).

   • • Matrix Forest Index (MF). This matrix depends on the idea of spreading over a tree which is characterized as the sub-graph that traverses complete hubs without shaping any cycle. The crossing tree might contain an out or less number of connections when contrasted with the first chart. The network forests hypothesis expresses that the quantity of traversing the tree in a chart is equivalent to the co-factor of any section of the Laplacian lattice of the diagram. Here, the term forest addresses the association of all established disjoints spreading over trees.

4.2.2. Probabilistic and maximum Likelihood-based approaches

For a given organization G(V, E), the probabilistic model upgrades a genuine capacity to set up a model that is made out of a few boundaries. Noticed information of the given organization can be assessed by this model pleasantly. By then, the probability of the presence of a non-existing connection (i,j) is assessed utilizing restrictive likelihood $P(A_{ij} = 1| \theta)$ . A few probabilistic models and the greatest probability models have been proposed in writing to gather missing joins in the organizations. The probabilistic models require more data like a hub or edge quality information, notwithstanding primary data. Removing these trait data is difficult; in addition, boundary tuning is likewise no joking matter in such models that limit their materialness. The greatest probability strategies are mind-boggling and tedious, so these models are not reasonable for the genuinely enormous organization (Clauset et al., 2008).

4.2.3. Dimensionality reduction based approaches

Dimensionality Reduction depends on network implanting and lattice decay. A portion of the procedures utilized for dimensionality decrease are Embedded connection expectation, Matrix factorization/disintegration-based connection forecast, and so on. Connection forecast is utilized when any association establishment is considered as a dimensionality decline system in which higher D layered centers (vertices) are intended to a lower ( $d \lt \lt D$ ) dimensional portrayal (implanting) space by protecting the hub area structures. All in all, find the implanting of hubs to a lower d-aspects with the end goal that comparable hubs (in the first organization) have comparative implanting (in the portrayal space) (Fukumizu et al., 2004).

Matrix factorization has been used extensively in a number of publications based on connect expectation and recommendation frameworks over the past ten years. Typically, the inactive elements are extracted, and each vertex in the inactive space is addressed using these elements. In a controlled or solitary organization, these depictions are utilized to connect expectations. To improve the anticipated findings, additional hub/connect or characteristic data may be used. Non-negative grid factorization and single-value decomposition have also been applied in the majority of the works.

4.2.4. Information diffusion based link prediction

In web-based interpersonal organizations, when a client sees that his neighbors share or re-post a snippet of data, the client will be affected to think about whether to share or re-post the data, which prompts data diffusion. Data dissemination permits clients to get or notice data that is past the extent of their social cycles. Besides, this peculiarity will impact the production of new connections. Prediction of this network information diffusion-based link prediction. Link Prediction licenses to derive absent or future associations in an organization. The organization association characterizes how data spreads through the hubs. Thus, the spreading might initiate changes in the associations and accelerate the organization’s advancement. LP calculations depend on various dispersion processes—Epidemics, Information, Rumor models, and so forth. Every one of these rare occasions of data dissemination-based connection link prediction techniques (Mack, 1985).

Organizations likewise powerfully develop designs in which associations might show up or vanish every once in a while. In this unique situation, interface forecast (LP) targets expecting future affiliations and different applications straightforwardly advantage from such forecasts, for example, kinship investigation in friendly organizations, affiliations and observing of suspects in psychological oppressor organizations, protein affiliations, suggestion frameworks in internet business, and applicable future joint efforts in participating organizations. Given an organization, we approach the two nearby and worldwide constructions, like the neighborhood of a hub, the distance among hubs, and the hubs’ local area structure. LP strategies target finding likely connections with primary impact dependent on a neighborhood or worldwide view, which can prompt distinctive expectation results. Normally, the nearby measurements are conventional and clear, while worldwide strategies need generous handling time and can’t deal with huge and thick organizations. Because of the networks’ intricate design and commotion nature, it is hard to anticipate future connections. Displaying data dispersion in web-based informal communities is a difficult issue, and different analysts contributed to the cycle to this end. In the LP research region, a few systems think about an irregular stroll in an organization, for example, DeepWalk (Perozzi et al., 2014), which has been proposed to look through logical edges utilizing uniform arbitrary strolls, and Node2vec (Grover & Leskovec, 2016), which investigates network areas through lopsided arbitrary strolls.

In the dissemination processes, Ally et al. (Ally & Zhang, 2018) proposed two overhauling models and thought about the impacts on data spreading in scale-free and little-world organizations. Be that as it may, the creators didn’t think about adding new edges or the impacts on the organizations’ design. In Li et al. (2016), the authors have tended to Sina Weibo and identified a significant component from the data dissemination process, which advanced LP execution. Wu et al. (2019) proposed a system called compelling hubs ID LP (INILP) to evaluate the significance of a hub in an organization by appointing every hub a positioning score. The impact of a hub addresses its capacity to spread data to different hubs. Be that as it may, the proposed measurements are primary hub rankings of centrality measures, not an appropriate persuasive spreading model, like pandemics, bits of gossip, or data proliferation. As of late, Wang et al. (2020) proposed a neighborhood antagonistic LP technique. However, they ignored the nearby impact of the dispersion elements on the connection development.

4.3. Community detection

Several community detection (Kumar et al. 2024; Mishra et al. 2024) algorithms already exist concerning the information diffusion procedure. We can broadly divide these procedures into four categories which are classical techniques, based on network centrality, overlapping in nature, and depending on stochastic optimization. Figure 5 illustrates the framework of community detection algorithms. In the following subsections, we have discussed all of them in detail.

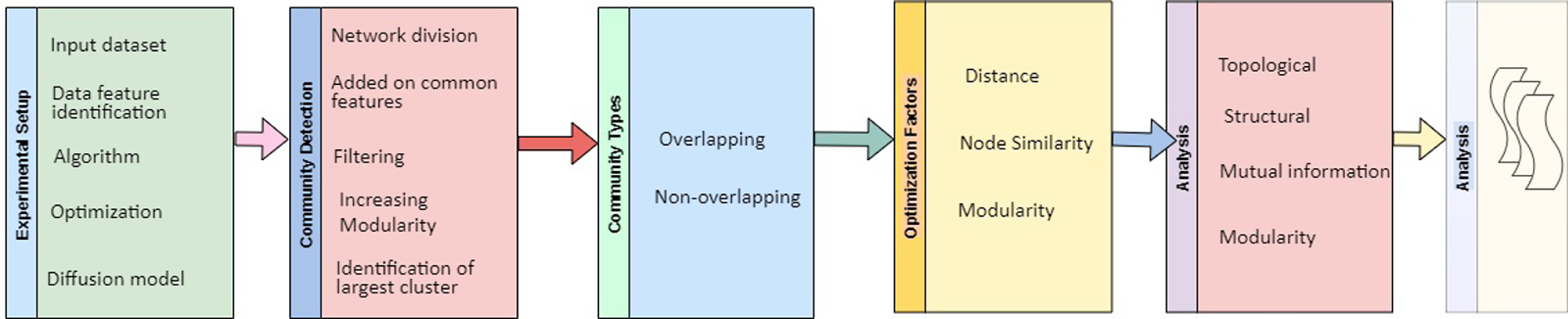
Figure 5. The community detection framework under information diffusion model (Das & Biswas, 2021b)

4.3.1. Classical community detection

Some of the classical community detection methods are utilized for information diffusion techniques. The techniques typically rely on network structure, node similarity, and community structures. It is suggested to use a hierarchical diffusion method to identify the community structure in Shen et al. (2010). The information is diffused from one community to another community in a hierarchical manner based on their placement in the network. In another work, Das and Biswas (2021a), the similarities in the network structure are considered for the information diffusion-based community detection (CSID) approach. The method has utilized the topology of the networks and considered only the importance of the central nodes. Information propagation with raw trajectory data is constructed for the diffusion process based on multiple similarity metrics in Liu and Wang (2016). A decentralized community detection algorithm based on the information diffusion method is proposed in Chen (2011). Ruan et al. (2013) have defined an edge strength measuring technique to find out communities utilizing edge-based data diffusion information. In another work, Yang et al. (2013) have employed several common metrics and traits along with edge strength measures between communities to define the structural boundaries. Some recent work (Bhattacharya & Sarkar, 2021) has demonstrated contagion and homophily-based information diffusion framework. These methods, however, have not taken into account the centrality considerations; instead, they may have uncovered communities based on network forms and structure.

4.3.2. Network centrality

To identify the core or influential node in any network, a number of network topology measurement metrics are utilized, including degree centrality, closeness centrality, betweenness centrality, eigenvector centrality, page rank, and clustering coefficient. Wang et al. (2015) have utilized centrality measures and structural holes to differentiate the important nodes from the dynamic networks utilizing individual nodes’ influence. These detected nodes are employed to forecast the data diffusion hub in the network. Bo et al. (2014) and Wu et al. (2015) have used edge strength measures and mutual information between the nodes for defining information propagation strategy. Based on the shared characteristics of the vertices, Li et al. (2015) have suggested a method for selecting seed vertices. In one of the recent works, seed nodes are selected by using different centrality measures and the k-core decomposition method (Devi & Tripathi, 2020). All the methods mentioned above have considered the structure of the network but ignored the overlapping formations. In the next subsection, we have emphasized the overlapping communities and network structures for information diffusion.

4.3.3. Overlapping community

Most social networks in real-life applications have shown overlapping parts within their structural formation. In recent times, a cascade information diffusion model has been proposed to simulate the evolution of communities (He et al., 2021). The fitness function of nodes is updated based on node similarity and uses a clustering methodology for discovering overlapping communities in dynamic networks. In another work, the overlapping communities are discovered based on the communication and sharing information of a node with its neighbors (Sun et al., 2018). A community-based seed selection method has considered the role of overlapping communities based on the gain in the nodes with respect to information diffusion (Wang et al., 2021). Kalantari et al. (2020) have proposed a node overlapping community detection technique based on node probing to distinguish the central nodes from the overlapping communities utilizing only the edge strength. Sun et al. (2020) have employed structural similarity measures to define the overlapping parts. In Ramezani et al. (2018), cosine similarities are used to find the number of cascades that belong among networks for discovering overlapping parts. One of the works (Alvari et al., 2014) has utilized a game theory-based method to optimize the overlapping part. Though the method has been revised, more efficient optimizing methods have been developed for community detection.

4.3.4. Stochastic optimization

There are several optimized community detection methods proposed for efficient information diffusion. In one of the popular methods, Hajibagheri et al. (2012), each node of the network is considered an agent. The interactions among the agents with their neighbors are optimized based on the proposed utility function. In Hajibagheri et al. (2013), the particle swarms method is used in network neighborhoods for optimizing objective functions. In another work, an approach is developed to discover information diffusion processes from online social networks based on modularity maximization (Obregon et al., 2019). Another technique based on a genetic algorithm is utilized in all types of networks for optimized community formation (Mozafari & Hamzeh, 2015). Recently, a multi-objective optimization model utilizing key node identification has been introduced (Kalantari et al., 2020). Through the study mentioned above, we have shown that most of the diffusion techniques, irrespective of their discovering nature, heavily depend on the network properties for high accuracy and efficiency.

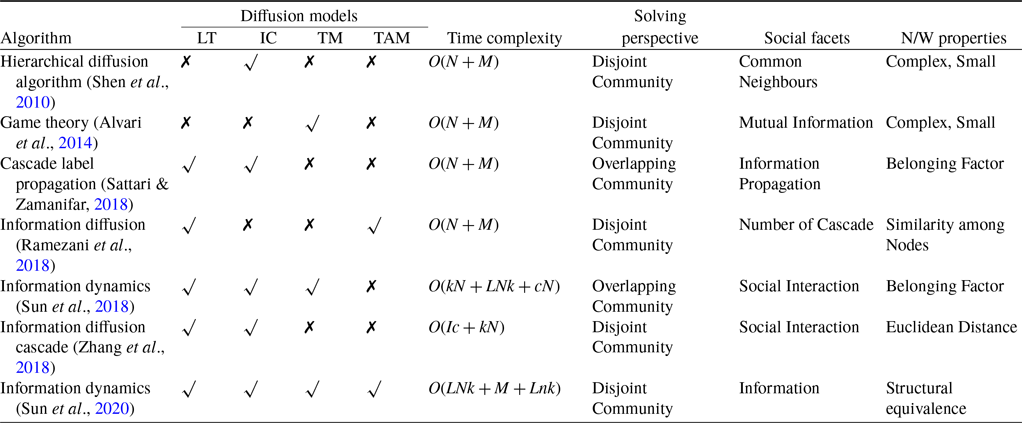
In Table 5, we have compared all the community detection algorithms based on the information dissemination model. Four diffusion models—the linear threshold (LT), independent cascade (IC), threshold model (TM), and time-aware model (TAM)—have been taken into account. We have defined the time complexity of each algorithm, solving perspective, social facets, and network properties individually. The comparison mentioned above among the algorithms gives us a clear idea about the impact of the techniques in this domain.

Table 5. The comparison of community detection algorithm based on information dissemination model (Das & Biswas, 2021b)

5. Evaluation metrics

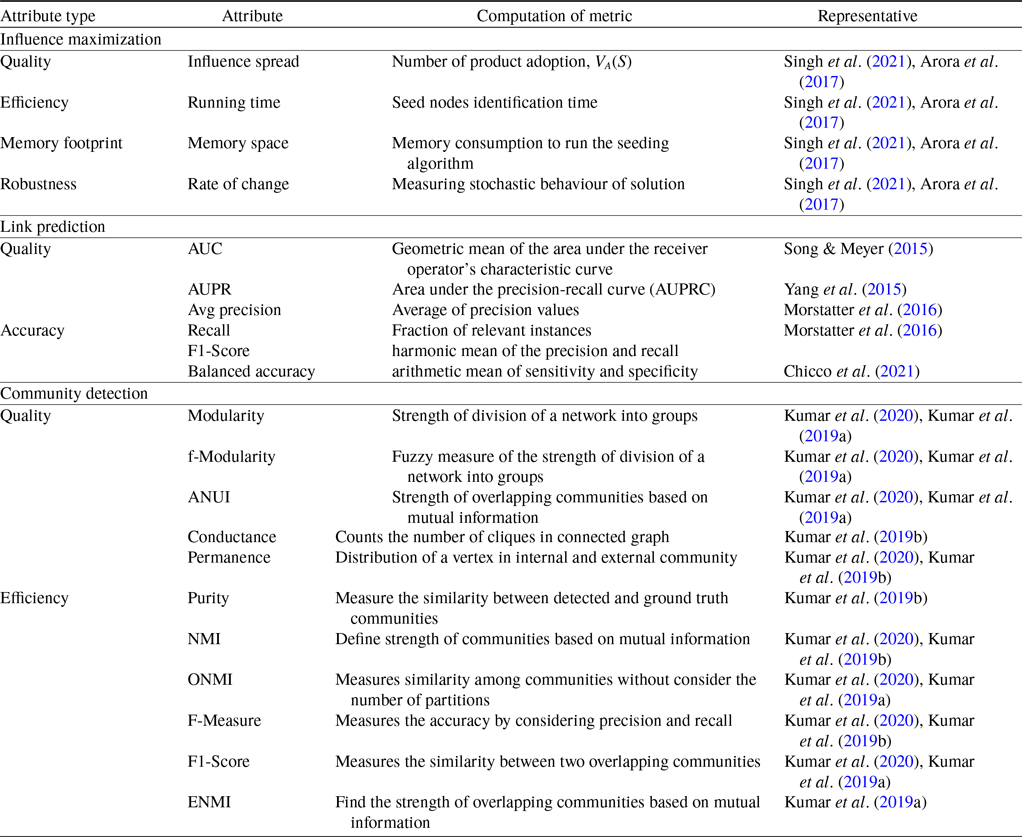
Evaluation metrics are crucial for assessing the quality and impact of research innovations. These metrics provide objective measures for assessing the importance, originality, and impact of the research on the field. Through the use of suitable evaluation metrics, researchers can assess the effectiveness of information diffusion models, deployment strategies, and proposed applications in a quantitative manner. In addition, these metrics allow for easy comparisons with other methodologies, making it easier to identify strengths, weaknesses, and areas that can be improved. Ultimately, the careful use of evaluation metrics ensures a high level of rigor and credibility in scholarly discourse, which leads to advancements in understanding and implementing information diffusion processes. This section is devoted to performance measures of different applications of information diffusion analysis. So we will discuss the evaluation metrics of influence maximization, link prediction, and community detection as illustrated in Table 6.

Table 6. The comparison of evaluation attributes (Kumar et al., 2020; Singh et al., 2021; Das & Biswas, 2021b)

5.1. Influence maximization evaluation metrics

Four matrices quality, efficiency, memory footprint, and robustness analyze the performance of IM algorithms.

1. 1. Quality. The influence spread estimates the quality of an IM approach, that is, the number of product adoption or users who a piece of information, news, idea, innovation, and product has influenced. Most of the traditional approaches ignore the effectiveness of seed users. Therefore, some of the recent works (Barbieri et al., 2012; Zhuang et al., 2013; Wang et al., 2017; Singh et al., 2019a) focus on contextual features to improve the effectiveness of seed users.

2. 2. Efficiency. The efficiency of IM algorithms has been measured by the running time of algorithms to produce the desired seed users. In general, running time will increase with the seed size. However, there are some exceptions like TIM (Tang et al., 2014) and IMM (Tang et al., 2015). The simulation-based approaches don’t have a better performance in terms of efficiency. Therefore some heuristic-based (Singh et al., 2019b ), meta-heuristics (Singh et al., 2019a; Singh et al., 2019b) and sampling (Jiang et al., 2011; Goyal et al., 2011b) methods have been introduced to overcome the limitations of simulation-based methods.

3. 3. Memory Footprint. The memory footprint is also a factor in addition to the time efficiency of an approach to measure the scalability of an algorithm. The memory footprint is evaluated by analyzing the memory required to run a seeding strategy for seed identification. The large size of the dataset leads to sampling methods (Jiang et al. 2011; Goyal et al. 2011b) to take a sample of datasets for identifying seed users based on structural and topological features.

4. 4. Robustness. Most IM algorithms are not robust as a slight modification in diffusion models leads to major changes in inactivation results. These IM algorithms only focus on quality, efficiency, and scalability while ignoring robustness. However, few works (Jung et al., 2012; Galhotra et al., 2016; He & Kempe, 2016; Mehmood et al., 2016) have been presented in the literature to ensure robustness on diffusion analysis.

5.2. Link prediction evaluation metrics

There are numerous conventional, straightforward, and fundamental connection expectation metrics used to evaluate Link Prediction. Mainly, it can be divided into two major parts, which are quality and accuracy as defined in Table 6.

5.2.1. Quality

Any link prediction quality calculation means the Precision of the calculation concerning the ground truth. Likewise, it signifies the strength of the networks. The accompanying boundaries are utilized to measure the nature of the local area discovery strategies. The metrics used to calculate the quality of link prediction are (Kumar et al., 2019a; Kumar et al., 2019b; Kumar et al., 2020):

1. 1. AUC (Area under the ROC Curve). A ROC (recipient working trademark bend) is a diagram showing the presentation of a grouping model at all order limits. This ROC plots two boundaries: True Positive Rate (TPR) and False Positive Rate (FPR). A ROC plots TPR versus FPR at various order edges. To register the focuses in an ROC, we could assess a calculated relapse model ordinarily with different characterization limits, yet all the same, this would be wasteful. Luckily, there’s a productive, arranging-based calculation that can give this data to us, called AUC (Fawcett, 2006).

2. 2. AUPR. It is the area under the precision-recall curve. It is a helpful metric to present imbalanced information in an issue setting where very much attention is in tracking down the positive models. The AUPRC is determined as the space under the PR bend. A PR bend shows the compromise between accuracy and review across various choice limits. The x-pivot of a PR bend is the review, and the y-hub is the accuracy. Rather than ROC bends, this is where the y-pivot is the review, and the x-hub is FPR. Like plotted ROC bends, the choice edges are verifiable in a plotted PR bend and are not displayed as a different hub. To compute AUPRC, we ascertain the region under the PR bend. There are numerous techniques for computation space under the PR bend, including the lower trapezoid assessor, the introduced middle assessor, and the average Precision (Saito & Rehmsmeier, 2015).

3. 3. Average Precision. It is the average precision values.

5.2.2. Accuracy

For any link prediction tracking method, accuracy signifies the precision of the calculation in regard to the calculation time. It relies a lot upon the size of the organization. A few boundaries are used to measure the productivity of the link prediction over a social network (Kumar et al., 2019b; Kumar et al., 2019a; Kumar et al., 2020).

1. 1. Recall. It is a metric that evaluates the quantity of right sure link forecasts (true Positive) made from all certain expectations (True Positive + False Negative) that might have been made in the complete network.

   (1) \begin{equation} recall=\frac{True\ Positive}{True\ Positive + False\ Negative} \end{equation}

2. 2. FI-Score. It is the harmonic mean of precision and recall.

   (2) \begin{equation} FI-Score=2 \times \frac{Precision\times Recall}{Precision+ Recall} \end{equation}

3. 3. Balanced Accuracy. It is the arithmetic mean of Sensitivity (true positive rate or recall) and specificity (true negative rate or 1 – false positive rate)

   (3) \begin{equation} Balanced\ Accuracy=\frac{Sensitivity + Specificity}{2} \end{equation}

5.3. Community detection evaluation metrics

The evaluation metrics of community detection are used to define the quality of the detected communities. Mostly, it can be divided into two major parts, which are quality and efficiency as defined in Table 6.

5.3.1. Quality

For any community detection algorithm, quality denotes the accuracy of the algorithm with respect to the ground truth. Also, it denotes the strength of the communities. The following parameters are used to measure the quality of the community detection techniques.

1. 1. Modularity. Modularity (Muhuri & Mukhopadhyay, 2021) measures the robustness of the partitions in a network. Modularity finds the density of connections between the nodes of the same community rest of the communities. The modularity Q of a graph with m number of edges can be defined as

   (4) \begin{equation} Q=\frac {1}{2m} \sum_{vw} \left[A_{vw}-\frac{k_v k_w}{2m}\right]\delta(c_v,c_w)\end{equation}
   $A_{vw}$ represents the connectivity of node i and j, $k_v$ denotes the sum of the weights of the edges incident with node v, $c_v$ is the community of node $v, \delta(c_v,c_w)$ is equals to 1 when v and w are in the same community, 0 otherwise.

2. 2. f-Modularity. It is a fuzzy measure that finds the mutual information among communities (Guo et al., 2021). The value decreases with the contraction of the community structures. f-modularity of a graph G can be denoted as

   (5) \begin{equation} f_{mod} (G)=max_{D\in C} \sum_{u,v} \left(\sigma f(D_{u,v})F_{u,v}-f^* (\sigma f (D_{u,v}))J_{u,v}\right)\end{equation}
   Here D distinguishes between frequency matrix F and random matrix J. C is a constraint set.

3. 3. ANUI. Average normalized unifiability and isolability (ANUI) analyses both unifiability and isolability to denote the quality of an overlapping community (Das & Biswas, 2021b). A graph G with k communities, unifiability of community $C_i$ to community $C_j$ is denoted as

(6) \begin{equation} unifiability (C_i)=\sum_{i=1}^k Unifiability (C_i,C_j)\end{equation}

(7) \begin{equation} isolability(C_i)=\frac{{(u,v)|u \in C_i (v)}}{{(u,v);(u,w)|u \in C_i (v) \& w \notin C_i}}\end{equation}

ANUI is denoted as

(8) \begin{equation} ANUI (C_i)= \frac{unifiability (C_i)+isolability (C_i)}{2}\end{equation}

1. 4. Conductance. It finds structural cohesiveness by incorporating external connections of the communities. Conductance of forecast community C is denoted as

   (9) \begin{equation} f(w)=\frac{E_w^{out}}{2.E_w^{in}+E_w^{out}}\end{equation}
   where $E_w^{out}$ and $E_w^{in}$ denote the number of edges that are outside and inside of the community C, respectively.

2. 5. Permanence. Permanence (Chakraborty et al., 2014) is a measure to find the pull of the neighborhood node on a particular node v. The internal clustering coefficient $c_in$ is also utilized to find the permanence perm(v).

   (10) \begin{equation} perm(v)=[\frac{I(v)}{E_{\max}(v)}\times \frac{1}{D(v)}] -[1-c_{in}(v)]\end{equation}
   where I(v) is internal connections, $E_{\max}(v)$ is the strength of internal community, and D(v) is the degree of node v.

5.3.2. Efficiency

For any community finding technique, efficiency denotes the accuracy of the algorithm with respect to the computation time. Also, it depends on the size of the network. Some parameters are utilized to measure the efficiency of the community detection algorithms.

1. 1. Purity. It assigns the detected community to the most frequent baseline (Lin et al., 2005).

   (11) \begin{equation} Purity(\Omega, C)=\frac{1}{N}\sum_k \max_j|\omega_k,c_j|\end{equation}
   where $\Omega$ is the set of ground truth communities.

2. 2. NMI. Normalized Mutual Information (NMI) finds the mutual dependence among the communities (Xie et al., 2013). NMI detects the similarity and quality between two divisions. Let the two communities are C and C ^′. Then NMI can be represented as

   (12) \begin{equation} NMI(C,C')=\frac {2I(C,C')}{H(C)+H(C')}\end{equation}
   where $H(.)$ represents entropy function and the mutual information $I(C, C')=H(C)+H(C')-H(C,C').$ No similarity and maximum similarity of two communities are denoted as the NMI value 0 and 1, respectively.

3. 3. ONMI. Overlap-Normalized Mutual Information (ONMI) is proposed in Van Lierde et al. (2019) for overlapping communities. The true and the predicted partitions are denoted by $C_l$ and $\overline{C_l}$ , respectively, where $1\leq l \leq K,\overline{K} $ . The number of true and predicted partitions are K and $\overline{K}$ , respectively. Then ONMI can be represented as:

   (13) \begin{equation} ONMI(X,\overline{X})=1-\frac{1}{2} (H(X|\overline{X})+H(\overline{X}|X))\end{equation}
   where $X_l$ = 1 denotes the event that a node belongs to $C_l$ and $\overline{X_l}$ = 1 denotes the event that a node belongs to $\overline{C_l}$ . Here normalized entropy of all $X_k$ given all $\overline{X_l}$ is
   (14) \begin{equation} H(X|\overline{X})= \frac{1}{k} \sum _{k} \frac{H(X_k|\overline{X})}{H(X_k)}\end{equation}
   High ONMI value is expected for the overlapping communities.

4. 4. F-Measure. it is the harmonic mean of both types of purity measures or between Precision and recall (Chakraborty et al., 2017).

   (15) \begin{equation} F-measure=\frac{2. Purity(\Omega,C). Purity(C,\Omega)}{Purity(\Omega,C)+Purity(C,\Omega)}\end{equation}

5. 5. F1-score. It measures the similarities between two overlapping communities (Chakraborty et al., 2017).

   (16) \begin{equation} F1=\frac{1}{2} (\frac{1}{\phi}\sum_{\phi_i \in \phi}F1(\phi_i,C_{g(i)}+ \frac{1}{C}\sum_{c_i \in C}F1(\phi_g,(i),c_i)))\end{equation}
   It represents the average of the F1-score of the best-detected partition and ground truth communities and the F1-score of the ground truth communities and best-detected partition.

6. 6. ENMI. Extended normalized mutual information (ENMI) compares the partitions with the baseline (Sun et al., 2018). ENMI is defined as

   (17) \begin{equation} ENMI(X|Y)=1-[H(X|Y)+H(Y|X)]/2\end{equation}
   where $H(X|Y)$ is denoted as
   (18) \begin{equation} H(X|Y)=1-\frac{1}{C'}\sum \frac{H(X_k|Y)}{H(X_k)}\end{equation}
   where X and Y denotes the random variables connected with the communities C and C’, respectively. $H(X|Y)$ is the normalized entropy of community X given community Y.

Table 7. Illustration of information diffusion challenges over different spplications (Kumar et al., 2020; Das & Biswas, 2021b; Singh et al., 2021)

6. Research challenges and future directions

The research challenges of information diffusion analysis have been categorized based on the applications. This section will discuss the challenges of information diffusion on influence maximization, link prediction, and community detection. These challenges are stated below in future directions.

6.1. Influence maximization

The computation of approximate influence spread is dependent on the diffusion process, which is stochastic. Therefore, it activates a different set of users in each diffusion round. Few efforts have been made to tackle these uncertainties, illustrated as follows.

• • Diffusion Process Modeling. The first challenge of information diffusion analysis corresponding to the IM problem is how to adapt the diffusion process for viral marketing. It is hard to accommodate user behavior about product adoption as the diffusion process is random. Therefore, some efforts (Kempe et al., 2003; Guille et al., 2013) have been made to tackle the adaption of the diffusion process for the IM problem by incorporating and extending traditional diffusion models.

• • Complexity and Optimality. Kempe et al. (2003) have proved that the IM problem is NP-hard under classical diffusion models. The influence spread computation under these models is computationally complex. Due to this, most simulation-based IM algorithms are inefficient and have some approximation guarantee to the optimal solution. However, heuristics and sampling methods are more time-efficient but less optimal. It is tough to find a near-optimal scalable solution. Therefore, most of the algorithms (Chen et al., 2010; Singh et al., 2019a; Singh et al., 2019b) focus on the trade-off between optimality and scalability.

• • Stochasticity of Diffusion Process. Most of the diffusion models are stochastic. Therefore, IM algorithms produce a different set of active users in each iteration from seed users due to the randomness of the diffusion process. So it is very tough to collect the final product adoption. However, some strategies like the mean and median of repeated iteration outcomes are applied to tackle the IM problem. For example, simulation-based methods (Kempe et al., 2003; Leskovec et al., 2007) perform $r=10\,000$ simulations while sampling methods (Cheng et al., 2013; Ohsaka et al., 2014) iterate multiple times on different sample episodes.

• • Stability and Robustness. Most of the IM methods are based on the assumption that the network structure is fixed while the network structure keeps on changing in the real world. Therefore, a slight change in the network can lead to a significant update in seed users. The authors of He & Kempe (2014) also stated that noisy influence probabilities could generate the inaccurate seed. Therefore some efforts (Jung et al., 2012; Galhotra et al., 2016; He & Kempe, 2016; Mehmood et al., 2016) have been made to find a robust solution for IM problem.

• • Incorporating Group Norms. Most of the literature considers only individual influence under the IC diffusion model and avoids group norms. However, people are also influenced by acquaintances and group norms such as trust, conformity, and context. People who share common interests, backgrounds, cultures, etc., are more inclined to each other’s thoughts. Therefore, some efforts (Li et al., 2011; Tang et al., 2013; Zhang et al., 2014) have been made to incorporate group norms with diffusion models. There are few possible future directions with group norms that can consider user profile information with group characteristics such as trust and conformity.

• • Adoption of Weaker Submodularity. The evaluation function is strict with the definition in general submodularity of approximate influence. This reduces the number of MC simulations under classical diffusion models for the IM problem. However, some of the advances (Li et al., 2011; Gionis et al., 2013; Galhotra et al., 2016) in the IM problem states that strictness of submodularity leads to no approximation guarantee of the solution. Because these advances are based on opinion formation and change. Therefore, it is required to adopt weaker submodularity in influence diffusion function to ensure some theoretical guarantee of the solution. There are some efforts (Das & Kempe, 2011) have made to weaken the submodularity of influence diffusion.

• • Incorporating Heterogeneous Diffusion Process. Most of the algorithms under the IM2 and MIM2 framework assume that every layer, relationship, or network has used the same diffusion models. However, in reality, each network has its diffusion method. Therefore, one possible future work can be the consideration of different diffusion processes across the layers and networks to achieve a more realistic scenario. However, some efforts (Zhan et al., 2015; Kuhnle et al., 2018) have been made to ensure heterogeneity across layers for the IM problem.

• • Considering Contextual Diffusion Models. Most of the classical IM algorithms ignore context-aware diffusion models by incorporating conformity, semantics, location, etc., with diffusion models for novel viral marketing applications. However, some efforts (Lee & Chung, 2015; Bozorgi et al., 2017; Su et al., 2018) have been made to consider contextual features with diffusion models. Still, most of these contextual features are unexplored.

• • Incorporating Conformity. Conformity is a crucial factor in how social influence spreads throughout societies. It describes how people tend to conform to the attitudes, beliefs, and behaviors of a majority group or societal norms. This phenomenon can occur through different mechanisms, such as informational conformity, where individuals conform because they believe others have relevant knowledge, or normative conformity, where individuals conform to gain social approval or avoid rejection. It supports processes of influence diffusion, where the adoption of certain behaviors or attitudes by a few individuals within a social network can lead to their widespread acceptance and adoption by others. Gaining insight into conformity is essential for understanding the development and evolution of social norms, as well as their influence on individual and collective behavior. Thus, to enhance the efficiency of the seed nodes, the authors in Li et al. (2011) made some attempts, yet many of these aspects remain unexplored.

6.2. Link prediction

This section discusses the challenges and efforts made to tackle these challenges, illustrated as follows.

• • Efficiency with Link Prediction. Because of the huge measure of information in interpersonal organizations, efficient and reliable link prediction addresses a critical test. To resolve this issue, researchers have proposed two calculations for interface expectation. The proposed calculations tackled the productivity issue by embracing low-rank factorization models while demonstrating extremely proficient contrasts with different techniques. This way, the review addresses a huge advance forward in the test of fostering a productive connection forecast model. Another significant issue that should be tended to worries the precision of connection forecast draws near. The test discoveries uncovered that the proposed approach beat numerous different techniques as far as exactness and versatility, and the related runtime were not exactly as seen in past examinations. Be that as it may, albeit the proposed approach improved connection forecast precision, it stays untested on large network information, which might see its proficiency become sabotaged (Fire et al., 2014).

• • Sparsity of Data. One more issue identified with interface forecast in marked SNs concerns the sparsity of information. To reduce this issue, researchers have proposed some effective methods, for instance, an imaginative methodology that is fit for investigating the client’s character utilizing web-based media. The acquired test results demonstrated an integral relationship between the marked connection forecast issue and character data. An intriguing cutting-edge technique for working with connect expectation is the utilization of worldly consistency in relational correspondence to focus on weighted edges in network diagrams. Another approach used is contrasted and different techniques, this strategy predicts interfaces regardless of whether there is a shortage in the quantity of edges required for investigation. A differentiating similitude-based connection expectation strategy is based on fuzzy connection significance. The technique performed well, utilizing two methodologies to accomplish its targets. Initially, for the determination of the neighbor, the distance between hubs was utilized. Besides, the fluffy connection significance was utilized to track down the pertinent connection. By utilizing these systems, the technique has acquired sound outcomes. The challenge for a sparse network is now been addressed but still needs a lot of attention as the network is getting sparse exponentially (Beigi et al., 2019).

• • Trusted Link Prediction. With the improvement of the Internet, an ever-increasing number of people or associations will more often than not discuss and communicate on the organizational stage. Through friendly stages, individuals can not just offer their sentiments about various items yet, in addition, express their perspectives on others, which extraordinarily improves individuals’ social exercises. Nonetheless, the fast improvement of social stages has filled them with many futile or bogus data and records. To rapidly and effectively peruse the substance for intrigued, clients as a rule add clients who have normal interests to the ‘trust list.’ simultaneously, to try not to peruse the substance not intrigued, clients generally add clients with inverse interests to the ‘doubt list.’ For instance, and have comparative interests and have some contention in a specific region. In this way, Twitter may follow and add to the boycott. We can assemble a marked interpersonal organization by catching the trust and doubt connections between clients. Through the trust/doubt connections in the marked informal community, we can not just know which clients the objective client has social associations with yet additionally know what sort of mentality the objective client embraces toward these clients. In any case, the social connections in an interpersonal organization are excessively inadequate, which truly upsets the extension of the client’s group of friends and further improves the social stage. Thus, it has become important to assist clients with finding all the more new companions or confided in clients. Luckily, clients have left a lot of verifiable conduct information (e.g., client’s appraising and remarks) on friendly stages, which gives great conditions to assessing the trust connections and comparability of inclinations between various clients. Notwithstanding, the way to deal with observing likely companions through shared interests actually faces many difficulties (Fan et al., 2019).

• • Level-wise Link Prediction. In complex networks, level-wise link prediction is used as it breaks the network into smaller networks and then predicts the link for each small network. The biggest challenge is dividing the complex network into smaller networks and then combining the link prediction of all networks and concluding it. The networks are so dynamic, and thus, predicting the link is a challenge! Trust, efficiency, and accuracy have to be maintained at every level as the next level depends on the previous link prediction. Thus it becomes a very challenging task (Kumar et al., 2020).

6.3. Community detection

There are several challenges associated with community detection concerning information diffusion. The challenges are mostly divided into five categories discussed here in detail.

• • Meaningful Communities. In an online social network, all the detected communities are not meaningful at all. The community detection methods might create some partitions that have no importance from the application point of view. In Shen et al. (2010), the problem has been addressed.

• • Running Time Optimization. Running time optimization is another important challenge in community detection as discussed in Das and Biswas (2021b). Though game-theoretic methods have performed better theoretically, their computational complexity should be reduced to achieve more efficiency.

• • Noise Removal. All the community detection algorithms are sensitive to noise. Different noise removal filters can be deployed to increase the technique’s accuracy. The problem has been discussed in Chen (2011) concerning a decentralized network.

• • Model Generalization. Researchers are very much focused on generalizing the model for different types of complex networks, including the independent cascade, biological, linear threshold, and epidemics models. In Li et al. (2015) and Devi and Tripathi (2020), authors have discussed the issue for encouraging futuristic models.

• • Sparse Network. If in a network, the number of 0 is greater than the number of 1, or the network consists of a huge number of isolated vertex. The community detection algorithms have failed to generate efficient communities as shown in Alvari et al. (2014). This challenge should be addressed for the refinement of the existing algorithms.

7. Open problems

In this section, we have discussed the open problems associated with information diffusion analysis.

• • How to aggregate information dissemination with reality? Most information dissemination models are not much closer to reality as these are the extension of classical diffusion models used across the domains. Therefore, it is necessary to strengthen these models to acquire actual word-of-mouth effects. Apart from extension, some new diffusion models are introduced for social network analysis. However, these models are more specific to applications and scenarios. Validation and correctness are also a concern as it is based on feedback from the Internet. Therefore, aggregating reality with information diffusion analysis is still much explored.

• • How to attain equivalence between feasibility and generality? Some diffusion models, like the competitive diffusion models, are not monotonic and submodular. So applicability of greedy-based methods is limited under such models. However, the literature lists some directions to handle these diffusion settings, such as nature-inspired optimization, deep learning, etc. The generality of existing methods under these settings is still a problem to explore.

• • How to obtain stochasticity of information diffusion process? Some studies suggest that noisy and inaccurate data for activation and influence probabilities can lead to incorrect adoption of information diffusion behavior (He & Kempe, 2014). Therefore, it is necessary to adopt real dynamics of information diffusion such as structural features, promotional impact, activation, and influence behavior to achieve the stochasticity of diffusion models. However, it has attracted the attention of researchers in recent years but is still much open to exploring this estimation.

• • How to acquire real-world complexity with information diffusion analysis? Most of the information diffusion analysis advances focuses on the topological structure and classical diffusion process. Therefore, these models are not consistent with reality as they ignore social, political, cultural, psychological, geographical, and environmental factors. So it is still an open problem to explore new possibilities of the information diffusion process to align with the complex reality.

• • How to deal with opinion change and negative influence in information dissemination? Most of the literature does not consider the adverse effect and opinion change in information diffusion analysis. These works consider positive impact only, and once a user is influenced by a piece of information, always intact with the same. This is not the case with actual scenarios where users are constantly changing and influenced by new information. Therefore, it is required to adopt negative and opinion change with information diffusion analysis. However, some studies (Li et al., 2014; Shen et al., 2015) are introduced regarding this but are still exploring.

• • How to tackle multiple, complementary, and competing ideas with information diffusion? In recent years, the applicability of information diffusion to some practical applications has attracted researchers to focus on more realistic assumptions. For example, viral marketing applications need to be more specific toward product and user characteristics rather than only topological structure. Similarly, considering users’ influence in a single online social network will ignore the user’s influence over other networks, leading to inaccurate estimation of influence. Therefore, incorporating multiple, complementary, and competitive ideas closer to reality needs to be explored.

• • How to assure ethical use of information propagated? The rapid growth of online social networks and their benefits leads to the urgency of users’ privacy protection. Users and network service providers need to understand the importance of privacy-preserving and ethical use of social media platforms. Ignoring the ethical use of platforms can have a severe effect on users and service providers. Therefore, privacy-preserving and ethical use can be considered with information-sharing perspective for exploring.

8. Concluding remarks

This paper surveyed the role, emergence, and significance of information dissemination for social network analysis. Information diffusion plays a key role in developing and proposing new solutions for social network applications. This study analyzed the various diffusion models with their vulnerabilities. Primarily, a brief discussion about the diffusion process component is presented. An in-depth information diffusion deployment and application is studied. A comparative analysis of the literature corresponding to influence maximization, link prediction, and community detection algorithms is discussed keeping the viewpoint of information diffusion. The study reveals the performance evaluation metrics for diffusion analysis applications. Finally, research gaps, challenges, and future prospects have been discussed, along with some open problems. This study will provide naive researchers with the basic and recent trends in information diffusion analysis with a better understanding and a good starting point for their research.