INTRODUCTION
Laser ablation is being widely used for surface structuring, chemical processing, and growth of thin films of a variety of materials. Textured surfaces with micro- and nano-scale morphological features show significantly altered physical, electrical, and mechanical properties (Latif et al., Reference Latif, Bhatti, Rahman and Rafique2012; Jelani et al., Reference Jelani, Bashir, Rehman, Ahamad, Haq, Yousaf, Akram, Afzal, Chaudhry, Mahmood, Hayat and Ahmad2013). A laser initiates a variety of processes upon interaction with the material through various energy transfer mechanisms depending on the irradiation conditions (Crouch et al., Reference Crouch, Carey, Warrender, Mazur and Genin2004). Observation of different mass removal regimes during the laser ablation of an aluminum target in air has been investigated by Cristoforetti et al. (Reference Cristoforetti, Legnaioli, Palleschi, Tognoni and Benedetti2008). Comparing the trends of line intensity of the atomized plasma mass and the crater volumes, four laser fluence ranges were identified where different mass removal mechanisms seem to occur. Various potential material removal mechanisms have been discussed together with their applicability for short pulse laser ablation of metallic matrices by Bleiner et al. (Reference Bleiner and Bogaerts2006). Lasers can induce topographical modifications through direct thermal ablations, optical interference patterning, splashing, spinodal breakdown, and hydrodynamic mechanisms (Crouch et al., Reference Crouch, Carey, Warrender, Mazur and Genin2004; Bleiner et al., Reference Bleiner and Bogaerts2006). A substantial work has been reported on the pulsed laser induced micro- and nano-structuring of various kinds of materials such as metals, semiconductors, dielectrics etc. (Sobhani et al., Reference Sobhani and Mahdieh2013; Bashir et al., Reference Bashir, Rafique and Husinsky2012b). Laser induced periodic surface structures, usually referred as ripples, are the commonly observed structures. Their formation mechanism is still not fully understood although a number of theories have been presented by various research groups (Crouch et al., Reference Crouch, Carey, Warrender, Mazur and Genin2004).
A substantial amount of work is reported on laser irradiation effects on various metals (Butt et al., Reference Butt, Dilawar, Naseem, Bashir and Ishtiaq2013; Trtica & Stasic et al., Reference Trtica, Batani, Redaelli, Limpouch, Kmetik, Ciganovic, Stasic, Gakovic and Momcilovic2013). But a very few work is reported on the laser induced nano-structuring for low melting point metals like zinc. Recently, the effect of laser focusing conditions on the surface modification and plasma parameters for zinc under ambient environment of vacuum has been studied. The formation of regular periodic surface structures by multi-pulse laser irradiation of zinc under vacuum condition has also been reported (Chen et al., Reference Chen, Liu, Liu and Zhao2012a; Reference Chen, Liu, Liu and Zhao2012b).
The nanosecond laser ablation of materials gives a dense and strongly ionized plasma plume of the ablated species due to laser interaction with the target and plume (Shaikh et al., Reference Shaikh, Rashid, Hafeez, Mahmood, Saleem and Baig2006b). Laser generated plasmas are technically important and have wide range of applications in ablation, deposition, and laser based ion sources (Chamorro et al., Reference Chamorro, Uzuriaga and Riascos2012). The plasma parameters such as electron temperature and density have been investigated as a function of various experimental variables, e.g., laser irradiance, nature, and pressure of ambient gas etc. (Shaikh et al., Reference Shaikh, Rashid, Hafeez, Mahmood, Saleem and Baig2006b; Hanif et al., Reference Hanif, Salik, Sheikh and Baig2013). The optimization of these parameters helps to understand the complex ablation mechanisms and control growth of structures (Sarkar et al., Reference Sarkar, Shah, Alamelu and Aggarwal2011). The presence of plasma strongly affects the ablation process and plays a key role for surface modification of the irradiated target. The ions/neutrals with known energy and flux can be applicable for laser assisted ion-sources and thin film growth (Ilyas et al., Reference Ilyas, Dogar, Ullah, Mahmood and Qayyum2012).
The confinement and shielding effect (Farid et al., Reference Farid, Bashir and Khaliq2012; Cristoforetti et al., Reference Cristoforetti, Legnaioli, Palleschi, Tognoni and Benedetti2008; Cabalín et al., Reference Cabalín, Romero, Baena and Laserna1999; Bleiner et al., Reference Bleiner and Bogaerts2006), enhanced chemical reactivity along mechanical action (Hermann et al., Reference Hermann, Boulmer-Leborgne, Dubreuil and Mihailescu1993) and additional energies produced by laser supported heat, shock, and combustion waves (Bäuerle et al., Reference Bäuerle2011) of plasma effectively participate for the growth of various kinds of structures. The effect of nature and pressure of ambient gas on laser induced plasma temperature and number density, the surface morphology of the irradiated metallic targets and co-relation between them has been investigated (Khan et al., Reference Khan, Bashir, Hayat, Rahman and Haq2013; Bashir et al., Reference Bashir, Farid, Mahmood and Rafique2012a). In the same context, generation and evolution of femtosecond laser induced silicon plasma by using time resolved spectroscopy along with the surface modification has been studied in various ambient gases at different laser fluences (Chen et al., Reference Chen, Wu, Yang, Baiquan, Yao, Rupp, Cao and Jingjun2012c).
Surface modification of zinc at micro- and nano-scale can enhance its optical absorption, thermionic and field emission properties of structured metal. The obtained results can also be applied for laser assisted deposition of metallic zinc films and implantation of zinc ions (Juan et al., Reference Juan, Min, Ying and Kui2013).
The aim of the present work is to investigate the effect of laser irradiance on the surface morphology of the irradiated zinc targets under ambient environment of argon. For this purpose, zinc targets have been exposed to various laser irradiances ranging from 13 GW/cm2 to 100 GW/cm2. The resulting surface modification has been analyzed using scanning electron microscope (SEM). In order to explore the effect of plasma on the ablation mechanisms, Laser-induced breakdown spectroscopy (LIBS) analysis has been also performed. The electron temperature and number density of the zinc plasma have been evaluated for various laser irradiances. SEM analysis has been correlated with the LIBS investigations.
EXPERIMENTAL DETAILS
A Nd:YAG laser (CRF200: Big Sky Laser Technologies, Quantel, France) with the central wavelength of 1064 nm, pulse duration of 10 ns, maximum pulse energy of 200 mJ, at a repetition rate of 1–10 Hz has been employed to perform the ablation and emission spectroscopy of zinc. Rectangular sheets of zinc with dimensions of 3 × 15 × 10 mm3 were used as target. Prior to laser treatment samples were grinded, polished, and ultrasonically cleaned with acetone for 30 min. Targets were placed in a stainless steel vacuum chamber, which was evacuated to a residual base pressure of about 10−3 mbar with the help of a rotary pump and then argon was filled at a pressure of 20 Torr. A lens of 50 cm focal length was used to focus the beam at right angle to the target surface with a spot size of 75 um. Two set of experiments were performed. In the first part, the targets were exposed to 200 laser pulses for SEM analysis, at four laser irradiances of 25 GW/cm2, 50 GW/cm2, 75 GW/cm2, and 100 GW/cm2 corresponding to laser pulsed energies of 50 mJ, 100 mJ, 150 mJ, and 200 mJ, respectively. The second set of experiment was performed for LIBS analysis. For this purpose, targets were exposed to single laser shot for laser irradiances ranging from 13 GW/cm2 to 100 GW/cm2.
The basic theme of the paper is to discuss the effects of plasma parameters on the laser-induced surface structuring of zinc. In this regards, the role of excitation temperature and electron density on the surface structuring of zinc has been addressed. The LIBS analysis is usually performed with single shot experiment. When SEM analysis of zinc with single pulse irradiation is performed no significant effects on the surface can be explored. Therefore samples were exposed with 200 numbers of overlapping pulses and then the corresponding surface modification is correlated with the accumulated effects of plasma parameters.
All targets (for both SEM and LIBS analysis) were exposed at a distance of 3 mm before the focus. This configuration was used to minimize the breakdown in the corresponding gas. The Surface morphology of the irradiated targets was investigated by using SEM (JEOL JSM-6480 LV). Emission spectra were collected by a LIBS2500 plus spectrometer system (Ocean Optics).
RESULTS AND DISCUSSION
SEM Analysis
SEM analysis reveals the surface modification of the zinc and illustrates the formation of craters for all fluences. However, an image of Figure 1a is an example which reveals the overall modified surface of zinc (crater and ripple — formation) after ablation at a laser irradiance of 100 GW/cm2 corresponding to pulse energy of 200 mJ. The whole crater is displayed (showing the crater + part of un-ablated surface) in Figure 1a. Whereas Figure 1b exhibits the magnified view of the central ablated area of zinc (inset of Fig. 1a) in which only ripples are seen.

Fig. 1. SEM images revealing the surface modification of zinc at laser irradiance of 100 GW/cm2. (a) The overall modified surface of zinc after laser ablation with crater and ripple- formation. (b) The magnified view of the central ablated area with only an appearance of ripples.
SEM images of Figure 2 illustrate the effect of laser irradiance on the surface morphology of the irradiated zinc targets. Figure 2a–2d represents the central ablated region. It is observed that laser irradiated surfaces are corrugated and rippled at central ablated areas. Figure 2a shows the growth of indistinct ripples for the lowest irradiance of 25 GW/cm2. When the irradiance increases up to 50 GW/cm2, distinct and elevated ripples are seen in Figure 2b. Their stability and smoothness also decreases. The protruding surface morphology shows sinusoidal behavior along with bead like structures. When the irradiance increases up to 75 GW/cm2 less distinct and narrow ripples are seen in Figure 2c. The periodicity does not change significantly. Another feature between the ripples is the remnants of turbulent melt flow. The regularity and periodicity of the ripples is enhanced at the highest irradiance of 100 GW/cm2 shown in Figure 2d. Their appearance becomes less distinct. Interference between the incident beam and the scattered wave is one of the proposed mechanism for the formation of these ripples (Sipe et al., Reference Sipe, Young, Preston and Van Driel1983). The average periodicity of the ripples varies from 20 to 30 µm but it is much greater than the wavelength of the incident laser beam (1.064 µm) for all irradiances. This suggests the exclusion of contribution of interference effects for the formation of these rippled structures. Certain hydrodynamical (instabilities) mechanisms may be more reasonably accounted for the growth of such kind of structures (Liu et al., Reference Liu, Jiang, Yang, Guan and Dai2011). Hydrodynamic expulsion is controlled by a competition between the inertial forces induced by the pressure field into the viscous melt and the surface tension that tends to maintain cohesion (Bleiner et al., Reference Bleiner and Bogaerts2006). These large scale ripple patterns look more like an unstable interface between the pool water and the wind blowing along its surface. The melted surface and expanding plasma plume above the target surface play the role of water and wind, respectively (Liu et al., Reference Liu, Jiang, Yang, Guan and Dai2011). These structures can also be considered as frozen morphology due to capillary waves (Young et al., Reference Young, Sipe and Van Driel1984). The elevation of the ripples increases from 25 GW/cm2 to 50 GW/cm2. However, further increase in laser irradiance up to 100 GW/cm2 causes reduction in the elevation and clarity of the ripples. The initial increase is attributed to the enhanced energy deposition. When the laser irradiance increases above 50 GW/cm2 ripples become less distinct. This is explainable on the basis of shielding effect of plasma (Farid et al., Reference Farid, Bashir and Khaliq2012). When the energy deposition increases plume temperature and density also increases. This plume with species of high kinetic energies and high fluxes will be able to absorb incoming laser radiations and therefore less laser energy will be deposited on the zinc target. This shielding effect will be responsible for reducing the electron temperature and number density of zinc plasma as has been confirmed by the LIBS analysis (Section 2).

Fig. 2. SEM images of the central ablated region of zinc targets at various laser irradiances of (a) 25, (b) 50, (c) 75, and (d) 100 GW/cm2.
SEM images of Figures 3a–3d present the inner boundaries of the laser ablated zinc. Cones and wave-like ridges are dominant structural features. Forward peaked cones with wide base and spherical top are seen at the surface irradiated with laser irradiance of 25 GW/cm2 as shown in Figure 3a. Preferential ablation due to evaporation resistive impurities, defects and hydrodynamic sputtering may be accounted for their formation (Kawakami et al., Reference Kawakami and Ozawa2003; Dolgaev et al., Reference Dolgaev, Fernández-Pradas, Morenza, Serra and Shafeev2006). Increasing the irradiance up to 50 GW/cm2 conical features are almost vanished and ridge formation is enhanced as shown in Figure 3b. Flakes are also formed in the inter ridged regions indicating the exfoliational sputtering. Further increase in irradiance up to 75 GW/cm2 increases the melted imprints in form of uplifted ridges and wavy patterns as shown in Figure 3c. Enhanced recoil pressure of the plasma splashes more material toward the boundary and causes ridge formation (Ko et al., Reference Ko, Pan, Hwang, Chung, Ryu and Costas2007). The melt displacement and expulsion become do minanat (Cristoforetti et al., Reference Cristoforetti, Legnaioli, Palleschi, Tognoni and Benedetti2008). Melt pool perturbation may also lead to the growth of Rayleigh-Taylor instability resulting in the formation of these wavy patterns (Willis et al., Reference Willis and Xu2000). When the irradiance increases to the 100 GW/cm2, cones with increased diameter, thick underlying ridges, and deep valleys are formed as shown in Figure 3d. Laser energy deposition at the boundary is smaller as compared to central ablated area because of the Gaussian distribution of the laser pulse. Shielding effects are therefore not dominant at peripheries due to lower irradiances (Cabalín et al., Reference Cabalín, Romero, Baena and Laserna1999; Bleiner, Reference Bleiner and Bogaerts2006). Hence, enhanced energy deposition with the increasing laser irradiance is responsible for the generation of these large size cones. The hydrodynamic pressure of the expanding plasma drives a shock wave toward the target surface in addition to the heating. The combined effect of heat and shock wave causes melting, evaporation, and sputtering of the target surface (Torrisi et al., Reference Torrisi, Gammino, Mezzasalma, Gentile, Krása, Láska, Rohlena, Badziak, Parys and Wolowski2003). SEM images of Figures 4a–4d show the outer boundary region of ablated zinc targets. It comprises of the displaced material from the center and re-deposited plasma condensates in addition to the direct laser heating effects. The structures observed at outer boundary are cones, flakes, and cavities. The heating of subsurface layer and rapid volume expansion of absorbed gases in the underlying pores of the target surface lead to the formation of these cavities (Lappalainen et al., Reference Lappalainen, Frantti and Lantto1998). Explosive relaxation of the mechanical stresses in the superficial layer may also be accounted for the formation of these cavities (Tokarev et al., Reference Tokarev2006). The size and number of cavities increase with the increase of laser irradiance up to a certain value and then decrease. It may be due to their re-filling with the melt.

Fig. 3. SEM images of the inner boundaries of the ablated zinc targets at various laser irradiances of (a) 25, (b) 50, (c) 75, and (d) 100 GW/cm2.

Fig. 4. SEM images of the outer boundaries of the ablated zinc targets at various laser irradiances of (a) 25, (b) 50, (c) 75, and (d) 100 GW/cm2.
LIBS Analysis
In order to correlate the ablation mechanism of irradiated zinc target with the plasma parameters, LIBS analysis was also performed. The plasma is characterized by its emission intensity, temperature, and number density of charged particles. All of these parameters are evaluated at various laser irradiances. Figure 5 shows the laser induced breakdown spectrum of zinc plasma obtained with 63 GW/cm2 irradiance in argon ambient at a pressure of 20 Torr. It contains different spectral lines from neutral zinc atoms at 334.5 nm, 468.0 nm, 472.2 nm, 481.0 nm, and 636.2 nm and from singly ionized zinc ions at 491.16 nm, 492.40 nm (shown in the inset) wavelengths. The rest of the lines correspond to Ar(I) at 696.54 nm, 763.51 nm, 810.37 nm, 811.53 nm, etc., and indicate its breakdown down (Shaikh et al., Reference Shaikh, Rashid, Hafeez, Jamil and Baig2006a). The obtained plasma is a mixture of ablated metal vapor and background gas.
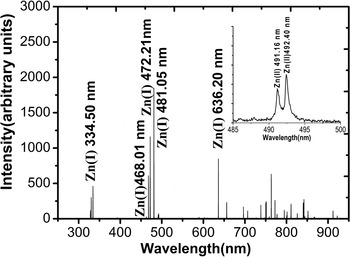
Fig. 5. The emission spectrum of laser induced zinc plasma under the ambient environment of Argon at a pressure of 20 Torr by using Nd:YAG laser (λ = 1064 nm, t =10 ns) at irradiance of 63 GW/cm2 .
Figure 6 shows the variation of emission intensity with the laser irradiance for the selected spectral lines corresponding to neutral zinc atoms. It depicts an initial increase of emission intensities with the increasing laser irradiance reaches a maximum then decreases followed by almost constant trend.

Fig. 6. (Color online) The variation of emission intensity of spectral lines of neutral zinc atoms at various laser irradiances ranging from 13 GW/cm2 to 100 GW/cm2.
The obtained emission spectra are used to calculate the excitation temperature and number density of the zinc plasma. Few assumptions are made prior to the calculations which generally hold good for the characteristics of the laser induced plasma in the concerned irradiance range. The plasma is considered to be in local thermal dynamical equilibrium (LTE) due to the dominance of collisional processes among the species and hence characterized by a homogenous temperature. The population in the excited states follows the Boltzmann distribution given by the following equation (Bashir et al., Reference Bashir, Farid, Mahmood and Rafique2012a; Harilal et al., Reference Harilal, Bindhu, Nampoori and Vallabhan1998; Iida et al., Reference Iida1990; Cristoforetti et al., Reference Cristoforetti, Palleschi, Salvetti and Tognoni2004; Hermann et al., Reference Hermann, Boulmer-Leborgne, Dubreuil and Mihailescu1993).
where λmn, I mn, g m, and A mn are wavelength, intensity, statistical weight, and transition probability of the upper level state m, respectively. On the right-hand side U(T), N(T), K, E m, and T e are partition function, total number density, Boltzmann constant, energy of the upper level state, and electron temperature, respectively. Boltzmann plot of the logarithmic term on the left-hand side versus the E m gives a straight line whose slope is equal to the −1/KT e under the assumption made that the distribution is Boltzmann. The relevant spectroscopic parameters for the transitions of the zinc plasma used in the calculation are listed in Table 1 and have been taken from Shaikh et al. (Reference Shaikh, Rashid, Hafeez, Jamil and Baig2006; NIST database).
Table 1. The spectroscopic data for the selected lines used to calculate the electron temperature and number density of laser induced zinc plasma (Sansonetti et al., 2005)

The transition lines at 334.5 nm (4s4d 3D3 → 4s4p 3P2), 468.0 nm (4s5s 3S1 → 4s4p 3P0), 472.2 nm (4s5s 3S1 → 4s4p 3P1), 481.0(4s5s 3S1 → 4s4p 3P2), and 636.2(4s4d 1D2 → 4s4p 1P1) are used for the calculation of electron temperature.
The variation of electron temperature with laser irradiance is shown in Figure 7. It increases slightly from 6126 K to 6240 K with increasing laser irradiance from 25 GW/cm2 to 63 GW/cm2. With further increase in laser irradiance from 63 GW/cm2 to 75 GW/cm2 the electron temperature drops down from 6240 K to 6030 K. With further increasing fluence up to a maximum value of 100 GW/cm2, the saturation with a negligible change (within error bar) in the electron temperature is achieved.
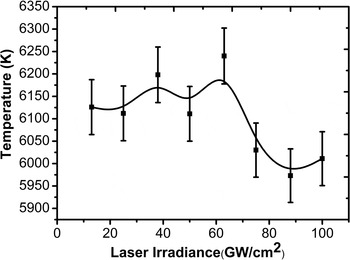
Fig. 7. The variation of electron temperature of laser induced zinc plasma obtained at various laser irradiances ranging from 13 GW/cm2 to 100 GW/cm2.
The plasma number density has been extracted from the profile of the line spectra obtained. Plasma species are under the influence of electric field of fast moving electron and slow ions. The perturbing electric field shifts the energy levels of the species leading to broadening called the Stark broadening. Other broadening mechanisms like Doppler and pressure broadening contribute little in this case and hence can be ignored. The relation of the full width at half maximum (FWHM) (Δλ1/2) of the stark broadened profile of the spectral lines and the electron number density of neon is given by the equation (Bashir et al., Reference Bashir, Farid, Mahmood and Rafique2012a; Harilal et al., Reference Harilal, Bindhu, Nampoori and Vallabhan1998; Iida et al., Reference Iida1990; Cristoforetti et al., Reference Cristoforetti, Palleschi, Salvetti and Tognoni2004; Hermann et al., Reference Hermann, Boulmer-Leborgne, Dubreuil and Mihailescu1993).
Where w is the impact width parameter. The Zn(I) line at 636.23 is used to calculate the electron number density.
The self-absorption for the spectral line 636.23 nm has been considered. The selected line must be sharp and the least broaden for fulfilling the criteria of minimum self-absorption. The selected line to be used for the calculations of number density is 632.23 nm for Zn(I) and it is sharp and the least broaden line as compared to all other lines of the obtained spectra. In order to check the self-absorption (SA) of a spectral line, following relation can be utilized for the evaluation of the parameter of SA (Cristoforetti et al., Reference Cristoforetti, Lorenzetti, Legnaioli and Palleschi2010b):
Where α = –0.54. The Δλ, w s, and N e is experimentally determined stark width, half width stark broadening parameter, and electron number density calculated from the H α line as (Sherbini et al., Reference Al-Sherbini, Al-Sherbini, Hegazy, Cristoforetti, Legnaioli, Palleschi, Pardini, Salvetti and Tognoni2005):
where Δλ is FWHM of H α line and C(λ, T) is a coefficient weakly dependent on density and temperature and has been tabulated in Griem et al. (Reference Griem1964). The value for Δλ is obtained by fitting the line with a Voigt profile and by considering the width of its Lorentzian component (Cristoforetti et al., Reference Cristoforetti, Lorenzetti, Legnaioli and Palleschi2010b). The Stark broadening parameter for 636.23 nm Zn(I) line has been taken from the work reported in Sherbini et al. (Reference El Sherbini, Aboulfotouh, Rashid, Allam, Al-Kaoud, Dakrouri and El. Sherbini2013). When SA value is nearly equal to 1 and it indicates that self-absorption effects are negligible while SA≪1 indicates that nonlinear effects are strong (Cristoforetti et al., Reference Cristoforetti, Lorenzetti, Legnaioli and Palleschi2010b). By putting data from our experiment the evaluated value of SA comes out to be nearly equal to one and therefore indicates that self-absorption is negligible for our case.
The self-absorption coefficient can also be calculated as (Sherbini et al., Reference Sherbini and Saad Al Aamer2012):
Where I(λ0) and I 0(λ0) are the spectral intensity of line in limit of negligible self-absorption and experimentally measured line height respectively. Δλ0 and Δλl are the Lorentzian component of spectral line if the line is optically thin and broadened FWHM of Lorentzian component of the same line because of self-absorption process respectively. n el and n eHα are the number densities evaluated from line under investigation and H α line, respectively. The obtained spectral line is plotted and fitted with the Lorentizan profile to obtain the FWHM and w (impact width parameter).
The variation of electron number density with increasing laser irradiance is shown in Figure 8. It increases from 1.3586 × 1018cm−3 to 1.4433 × 1018cm−3 with increasing laser irradiance from 25 GW/cm2 to 63 GW/cm2. With further increase in laser irradiance from 63 GW/cm2 to 75 GW/cm2 it drops down slightly to a value of 1.4296 × 1018 cm−3. With further increasing fluence up to a maximum value of 100 GW/cm2, the saturation with a negligible change (within error bar) in the electron density is achieved.

Fig. 8. The variation of electron number density of zinc plasma at various laser irradiances ranging from 13 GW/cm2 to 100 GW/cm2.
The observed trend in electron temperature and number density is divided into three regions: an initial increase with the increase of laser irradiance reaches a maximum at 63 GW/cm2 in the first region, then decrease in the second region, and finally saturation is achieved in the third region. This can be explained as follows: when a nanosecond laser interacts with the material it heats up the target until its melting point is reached and eventually causes it to eject into the form of vapor (Farid et al., Reference Farid, Cong, Hongbei and Hongbin2013). Initially, at lower irradiances the ablation rate increases with the increase of laser irradiance which in turn increases the temperature and charge particle density in the plasma (Luo et al., Reference Luo, Zhao, Sun, Gao, Tang, Wang and Zhao2010). The background pressure also effectively confines the plasma species which further adds to increase the temperature and density of charged particle by reducing its expansion rate. The background argon ambient at a pressure of 20 Torr is seemed to be sufficient to confine the generated target vapors. Plasma reaches its maximum temperature and number density at 63 GW/cm2. This vapor plume continues to absorb the laser energy through inverse-bremsstrahlung and direct photo ionization processes and start to shield the target from the laser irradiation (Harilal et al., Reference Harilal, Bindhu, Nampoori and Vallabhan1998). Further increase in the irradiance reduces energy deposition to the target due to enhanced shielding effect of the plasma which leads to decrease the electron temperature and number density. At still higher irradiances the saturation region is observed due to the formation of a self-regulating regime in addition to the shielding effect (Cristoforetti et al., Reference Cristoforetti, Legnaioli, Palleschi, Tognoni and Benedetti2008; Bleiner et al., Reference Bleiner and Bogaerts2006). In this regime, the density, temperature, and dimensions of plume adjust in such a way that plasma absorb the same amount of laser energy to maintain the self-regulating regime (Harilal et al., Reference Harilal, Bindhu, Nampoori and Vallabhan1998; Hafeez et al., Reference Hafeez, Shaikh, Rashid and Baig2008).
Cristoforetti et al. (Reference Cristoforetti, Giacomo, Dell'Aglio, Legnaioli, Tognoni, Palleschi and Omenetto2010a) has addressed the criteria for the establishment of LTE in addition to the McWhirter criterion. The McWhirter criterion is a necessary but not the sufficient condition to ensure the existence of LTE in plasma. The condition of LTE has been assessed for plasma in three states namely stationary and homogenous, transient and homogeneous, and transient and inhomogeneous. Considering our plasma as transient and homogenous, we have fulfilled the criteria for LTE by evaluating the following two conditions: (1) The McWhirter criteria n e (cm−3) = 1.6 × 1012 (T)1/2(ΔE nm)3 has been fulfilled (Cristoforetti, Reference Cristoforetti, Giacomo, Dell'Aglio, Legnaioli, Tognoni, Palleschi and Omenetto2010). For the excitation temperature T e = 6240 K, the number density of neon comes out to be of the order of 1014. (2) For homogenous and transient plasma, if the time needed for the establishment of excitation and ionization equilibrium (relaxation time) is much shorter than the time for variation of thermodynamic parameters (mainly neon) then the plasma evolves through quasi-equilibrium near LTE states (Cristoforetti et al., Reference Cristoforetti, Giacomo, Dell'Aglio, Legnaioli, Tognoni, Palleschi and Omenetto2010a). The rate coefficient for the collisional excitation from ground to first excited state of the resonance series being the slowest one has been considered for the rough estimation of this relaxation time. This can be expressed as (Cristoforetti et al., Reference Cristoforetti, Giacomo, Dell'Aglio, Legnaioli, Tognoni, Palleschi and Omenetto2010a):
 $$\eqalign{t_{\rm rel}=1/n_{e} \lt \!{\rm \nu}\, a_{12} \gt & =6.3 \times 10^{14} \Delta E_{21}\lpar KT\rpar ^{1/2} \cr &\exp \lpar \Delta E_{21}/KT\rpar /n_{e}f_{12} \lt \!g \gt .}$$
$$\eqalign{t_{\rm rel}=1/n_{e} \lt \!{\rm \nu}\, a_{12} \gt & =6.3 \times 10^{14} \Delta E_{21}\lpar KT\rpar ^{1/2} \cr &\exp \lpar \Delta E_{21}/KT\rpar /n_{e}f_{12} \lt \!g \gt .}$$Where t rel is relaxation time, ΔE 21 and KT are both expressed in eV. The f 12 is the transition oscillator strength, <g> is effective gaunt factor and ne is number density in cm−3. The calculated time (of the order of 10−9s) came out to be reasonably shorter than the typical decay time of electron temperature and number density (approximately 1 µs).
LIBS analysis can be well correlated with the SEM investigations. The initial increase in T e and n e with the increasing laser irradiance is responsible for the growth of distinct and well defined ripples. After obtaining the maxima, T e and n e decrease because of shielding effect and formation of self-regulatory region. Due to less energy deposition of electrons to the lattice the grown structures become diffusive and narrow.
CONCLUSIONS
The effect of various laser irradiances (ranging from 13 GW/cm2 to 100 GW/cm2) on surface morphology and plasma parameters of zinc have been investigated. SEM investigation revealed the formation of rippled structures at the center, whereas cones and cavities are seen at the boundary of ablated zinc targets. Initially with the increase of laser irradiance distinctness of the ripples increases due to enhanced energy deposition. They become less pronounced with the further increase in irradiance due to enhanced shielding effect. Due to the Gaussian distribution of laser pulse, the energy deposited at boundary is smaller as compared to the center. Hence the shielding effect is not produced at the boundaries and energy deposition continues to increase with the increase of laser irradiance. This results in the growth of large size structures and enhanced melting effects at the inner and outer boundary regions respectively at high irradiances. This trend is well correlated with the LIBS results in which an initial increase in the electron temperature and density with the increase of laser irradiance up to a 63 GW/cm2 and then a decrease and saturation is observed at high irradiances.











