No CrossRef data available.
Article contents
Alteration in the sum of alternating series by simple rearrangement
Published online by Cambridge University Press: 23 January 2015
Extract
It is well known that the sum of an absolutely convergent series is invariant under rearrangement of its terms. On the other hand, a conditionally convergent series, that is one which converges but the sum of whose absolute values is unbounded, can be rearranged to have any sum whatsoever, or diverge in any desired manner (see for example [1, §44]). A simple examplS of a conditionally convergent series is the alternating harmonic series (AHS), 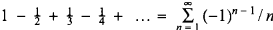 . In [2], the following theorem on rearrangement of the AHS was proved:
. In [2], the following theorem on rearrangement of the AHS was proved:
Theorem A: The AHS remains convergent under a simple rearrangement (i.e. the sub-sequence of its positive terms and the sub-sequence of its negative terms are in their original order) when p of its positive terms alternate throughout with q of its negative terms, and the alteration in sum is 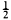 (p/q).
(p/q).
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2013


