Articles
Alteration in the sum of alternating series by simple rearrangement
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 193-197
-
- Article
- Export citation
Reflections on the Woolwich Ferry
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 198-204
-
- Article
- Export citation
Some remarkable integrals derived from a simple algebraic identity
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 205-209
-
- Article
- Export citation
Folding a triangle
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 210-217
-
- Article
- Export citation
Revisiting the sliding ladder
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 218-223
-
- Article
- Export citation
Relations on Sets
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 224-233
-
- Article
- Export citation
From golden-ratio equalities to Fibonacci and Lucas identities
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 234-241
-
- Article
- Export citation
Could, or should, the ancient Greeks have discovered the Lucas-Lehmer test?
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 242-255
-
- Article
- Export citation
The gaps between sums of two squares
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 256-262
-
- Article
- Export citation
Notes 97.17 to 97.38
97.17 On products of multiplicative functions
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 263-264
-
- Article
- Export citation
97.18 Variatins on twin primes
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 265-268
-
- Article
- Export citation
97.19 Shifting the origin to solve quartic equations
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 268-270
-
- Article
- Export citation
97.20 Evaluating a common improper integral
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 270-272
-
- Article
- Export citation
97.21 Some more on Estermann and Pythagoras
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 272-273
-
- Article
- Export citation
97.22 A proof that the series
 is convergent for p > 1
is convergent for p > 1
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 273-274
-
- Article
- Export citation
91.23 On the monotonocity of the correction term in Ramanujan's factorial approximation
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 274-275
-
- Article
- Export citation
97.24 A constant in a formula of Ramanujan
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 276-277
-
- Article
- Export citation
97.25 Error terms for Jensen's and Levinson's Inequalities
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 277-280
-
- Article
- Export citation
97.26 The cosine rule in three dimensions and de Gua's theorem
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 281-284
-
- Article
- Export citation
97.27 Two rectangles and an intersection
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 284-290
-
- Article
- Export citation

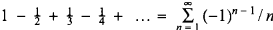 . In [2], the following theorem on rearrangement of the AHS was proved:
. In [2], the following theorem on rearrangement of the AHS was proved: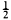 (
(
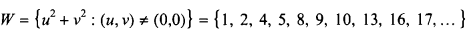
 is convergent for
is convergent for