No CrossRef data available.
Article contents
Equal sums, sums of squares and sums of cubes
Published online by Cambridge University Press: 24 February 2022
Extract
Consider the problem of finding triples of numbers (x1, x2, x3) and (y1, y2, y3) satisfying(1) and (2)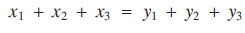 $${x_1} + {x_2} + {x_3} = {y_1} + {y_2} + {y_3}$$
$${x_1} + {x_2} + {x_3} = {y_1} + {y_2} + {y_3}$$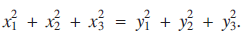 $$x_1^2 + x_2^2 + x_3^2 = y_1^2 + y_2^2 + y_3^2.$$
$$x_1^2 + x_2^2 + x_3^2 = y_1^2 + y_2^2 + y_3^2.$$
Information
- Type
- Articles
- Information
- Copyright
- © The Authors, 2022. Published by Cambridge University Press on behalf of The Mathematical Association
References
Jameson, G. J. O., Monotonicity of the mid-point and trapezium estimates for integrals, Math. Gaz. 105 (November 2021) pp. 433–441.10.1017/mag.2021.110CrossRefGoogle Scholar
Jameson, G. J. O., Counting zeros of generalised polynomials: Descartes’ rule of signs and Laguerre’s extensions, Math. Gaz. 90 (July 2006) pp. 223–234.10.1017/S0025557200179628CrossRefGoogle Scholar


