We define a Fibonacci fraction circle to be a circle passing through an infinite number of points whose coordinates are of the form 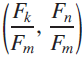$\left( {{{{F_k}} \over {{F_m}}},{{{F_n}} \over {{F_m}}}} \right)$ , where the F’s are Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …). For instance, the circle (1)

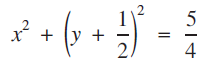$${x^2} + {\left( {y + {1 \over 2}} \right)^2} = {5 \over 4}$$

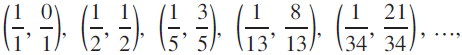$\left( {{1 \over 1},{0 \over 1}} \right),\,\left( {{1 \over 2},{1 \over 2}} \right),\,\left( {{1 \over 5},{3 \over 5}} \right),\,\left( {{1 \over {13}},{8 \over {13}}} \right),\left( {{1 \over {34}},{{21} \over {34}}} \right),\,...,$

A golden right triangle of first type is a right triangle such that the shortest side is the golden section of the hypotenuse as defined in [1], [2]. If we consider a golden rectangle and one of its diagonals, we obtain a right triangle with the shortest side being the golden section of the other side; this right triangle will be named golden right triangle of second type.

If a circle rolls without slipping around an equal fixed circle, then a point carried by the rolling circle traces out a limaçon of Pascal. (This is Etienne Pascal, father of Blaise. The word limaçon is derived from the Latin limax, a snail.) If the fixed and rolling circles have radius 1, and the point P carried by the rolling wheel is distant a from its centre, then for a > 1 the limaçon has an inner and an outer loop, joining up at a node. For a = 1 it has a cusp, and is then a cardioid, so-called because it is heart-shaped. See Figure 1, where we have plotted the cases a = $${3 \over 4}$$ , a = 1 and a = $${3 \over 2}$$ .

Euler’s striking proof of the fact that the infinite sum

${1 \over {{1^2}}}\, + \,{1 \over {{2^2}}}\, + \,{1 \over {{3^2}}} + \,...\, + \,{1 \over {{n^2}}} + \,...\, = {{{\pi ^2}} \over 6}$

$\zeta (s)\zeta = \sum\limits_{n = 1}^\infty {{1 \over {{n^s}}}} $

$\zeta (2)$

$\sum\limits_{n = 0}^\infty {{1 \over {{{(2n + 1)}^2}}} = {{{\pi ^2}} \over 8}} .$

It is tempting to accept bets when the outcome has a positive expectation favouring the bettor. We examine situations where this is not enough of a criterion as a basis for betting. The argument we present shows that the probability of winning the bets in the long run has to be qualified in a certain way beyond positive expectation. We introduce an alternative index as a criterion to recommend to bettors.

"What should we use?" seems to be the question when one approaches a plane geometry problem. In many ways, Euclidean geometry is a laboratory in the realm of logic, an ideal place where one can see how alternative methods can be employed to solve problems. What detail might represent a hint? And from among many choices, what method could one consider? Does the geometric structure suggest a certain type of approach?

Consider the problem of finding triples of numbers (x1, x2, x3) and (y1, y2, y3) satisfying (1)

$${x_1} + {x_2} + {x_3} = {y_1} + {y_2} + {y_3}$$

(2)

$$x_1^2 + x_2^2 + x_3^2 = y_1^2 + y_2^2 + y_3^2.$$

This is a follow-up to a recent Gazette Article by Abel [1]. We investigate probabilistic equalisation problems proposed in [1] using the Pólya urn, and characterise them through simple random walks.

In 1631, Johannes Faulhaber published the result that sums of the form

$$\sum\limits_{i = 1}^n {{i^k}} = {1^k} + {2^k} + \,...\, + {n^k}$$

Figure 1 shows a triangle ABC with the midpoints A′, B′ and C′ of its sides. The line segments AA′, BB′ and CC′ are called the medians, and the point G of their intersection the centroid. The line segments AG, BG and CG will be called, for lack of a better name, the semi-medians. It is interesting that the medians of any triangle can serve as the side lengths of some triangle. This property of the medians is referred to as the median triangle theorem in [1, §473, page 282], and is discussed, together with generalisations to tetrahedra and higher dimensional simplices, in [2].

Ask anyone who has studied mathematics to a moderate level how many trigonometric functions there are and one is likely to be presented with a range of answers depending on what the person being asked is most likely to remember. Perhaps the ‘calculator button’ three of sine, cosine, and tangent will come to mind as these are the three trigonometric functions found on any standard scientific calculator. At a stretch, perhaps the names for their respective reciprocals, cosecant, secant and cotangent, will be recalled. Beyond the modern standard six, looking at calculus or trigonometric texts published prior to 1900 one soon discovers others going by strange names such as versine, haversine, or coversine (see, for example, [1, pp. 53, 63]). There are at least six others with as many as perhaps ten to twelve having received a name at one time or another. Today all these additional trigonometric functions considered important enough to grace the pages of texts in centuries past have fallen by the wayside, to be largely forgotten in favour of the modern standard six. Of course the pedant amongst us would say there is only one trigonometric function, the sine function, which currently stands as the preferred fundamental trigonometric entity, with all others being simple variations of this function, and they would not be incorrect in asserting this. But having the current standard six seems about the right balance between the minimalistic on the one hand and convenience on the other hand.

Given positive numbers xj, yj such that $\sum\limits_{i = 1}^n {{x_j}} = \sum\limits_{j = 1}^n {{y_j}} $ , it can happen that $\sum\limits_{j = 1}^n {x_j^2} = \sum\limits_{j = 1}^n {y_j^2} $ : for example, $({x_j}) = (7,\,3,\,2),\,({y_j}) = (6,\,5,\,1)$ . However, such cases are exceptional.

A slogan that you find on the back of a pack of Skittles candy says ‘No two rainbows are the same. Neither are two packs of Skittles. Enjoy an odd mix.’ An online blog [1] describes how the blogger found two identical packs of Skittles, among 468 packs with a total of 27,740 Skittles. Meticulously collecting the data for this experiment was apparently triggered by some earlier calculations. More precisely, the blogger writes: